一阶常微分方程初等解法
摘 要: 本文通过对一阶微分方程的初等解法的归纳与总结,以及对变量分离,积分因子,微分方程等各类初等解法的简要分析,同时结合例题把常微分方程的求解问题化为积分问题,进行求解.
关键词: 一阶常微分方程;变量变换;恰当微分方程;积分因子
First-order Differential Equation With The Pirmary Method For Nalysis
Abstract: Based on the first-order differential equations of the elementary solution of the induction and conclusion, and the separation of variables, integrating factor, equations, etc. summary analysis of various elementary solution, combined with examples the problem of solving ordinary differential equations into integral on the problem solving.
Key Words: First-order differential equation;cain declined equations;variable transformation;appropriate differential equation; integrating factor
1.预备知识
1. 1 变量分离方程
形如
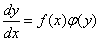 (
(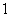 )
)
的方程,称为变量分离方程, ,
,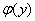 分别是
分别是 ,
,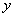 的连续函数.这是一类最简单的一阶函数.
的连续函数.这是一类最简单的一阶函数.
如果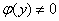 ,我们可将(
,我们可将(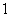 )改写成
)改写成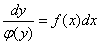 ,这样变量就分离开来了.两边积分,得到
,这样变量就分离开来了.两边积分,得到
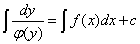 ,
,
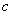 为任意常数.由该式所确定的函数关系式
为任意常数.由该式所确定的函数关系式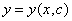 就是常微分方程(
就是常微分方程(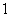 )的解.
)的解.
1. 2 积分因子
恰当微分方程可以通过积分求出它的通解.因此能否将一个非恰当微分方程化为恰当微分方程就有很大的意义.积分因子就是为了解决这个问题引进的概念.
如果存在连续可微函数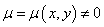 ,使得
,使得
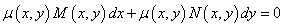
为一恰当微分方程,即存在函数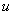 ,使
,使
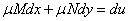 ,
,
则称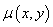 为方程
为方程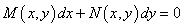 的积分因子.
的积分因子.
函数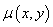 为
为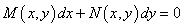 积分因子的充要条件是
积分因子的充要条件是
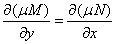 ,
,
即
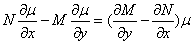 .
.
假设原方程存在只与 有关的积分因子
有关的积分因子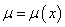 ,则
,则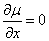 ,则
,则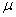 为原方程的积分因子的充要条件是
为原方程的积分因子的充要条件是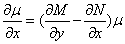 ,即
,即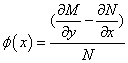 仅是关于
仅是关于 的函数.此时可求得原方程的一个积分因子为
的函数.此时可求得原方程的一个积分因子为 .同样有只与
.同样有只与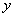 有关的积分因子的充要条件是
有关的积分因子的充要条件是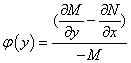 是仅为
是仅为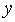 的函数,此时可求得方程(
的函数,此时可求得方程(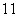 )的一个积分因子为
)的一个积分因子为
1. 3恰当微分方程
考虑微分形式的一阶微分方程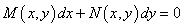 (
(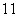 ),如果该式的左端恰好是某个二元函数
),如果该式的左端恰好是某个二元函数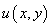 的全微分,即
的全微分,即
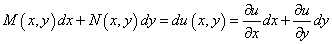
则称(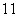 )为恰当微分方程.
)为恰当微分方程.
对于一阶微分方程
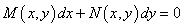 ,
,
若有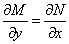 ,则该方程必为恰当微分方程.我们接着讨论如何求得该恰当微分方程的解.我们可以把
,则该方程必为恰当微分方程.我们接着讨论如何求得该恰当微分方程的解.我们可以把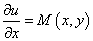 看作只关于自变量
看作只关于自变量 的函数,对它积分可得
的函数,对它积分可得 ,由此式可得
,由此式可得
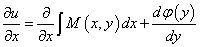 ,
,
又因为有 ,故
,故
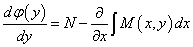 ,
,
对该式积分可得
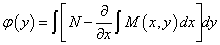 ,
,
将该式代入,得恰当微分方程的通解为
 .
.
2.基本方法
2. 1一般变量分离
形如
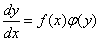 (
(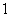 )
)
的方程,称为变量分离方程, ,
,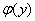 分别是
分别是 ,
,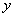 的连续函数.这是一类最简单的一阶函数.
的连续函数.这是一类最简单的一阶函数.
如果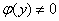 ,我们可将(
,我们可将(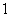 )改写成
)改写成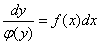 ,这样变量就分离开来了.两边积分,得到
,这样变量就分离开来了.两边积分,得到
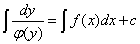 ,
,
 为任意常数.由该式所确定的函数关系式
为任意常数.由该式所确定的函数关系式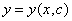 就是常微分方程(
就是常微分方程(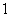 )的解.
)的解.
2. 2齐次微分方程
2. 2. 1齐次微分方程类型一
一阶线性微分方程
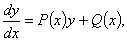
其中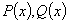 在考虑的区间上是
在考虑的区间上是 的连续函数,若
的连续函数,若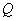
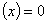 ,变为
,变为

称为一阶齐次线性微分方程,若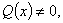 称为一阶非齐次线性微分方程.变易分离方程,易求得它的通解为
称为一阶非齐次线性微分方程.变易分离方程,易求得它的通解为
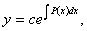
这里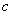 是任意常数.
是任意常数.
2.2.2齐次微分方程类型二
有些方程本不是可分离变量微分方程的类型,但经过变量变换可化为分离变量的微分方程.可分为三种情况来讨论:
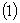
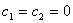 的情形
的情形
这时,有
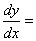
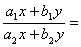
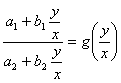
因此,只要作变换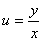 ,则方程就转化为变量分离方程.
,则方程就转化为变量分离方程.
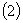
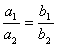
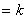 的情形.
的情形.
这时方程可写为
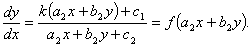
令 ,则方程化为
,则方程化为
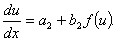
这是变量分离方程.
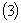
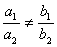 及
及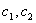 不全为零的情形
不全为零的情形
因为方程右端分子,分母都是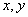 的一次多项式,因此
的一次多项式,因此
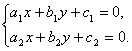
代表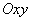 平面上两条相交的直线,设交点为
平面上两条相交的直线,设交点为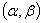 ,若令
,若令
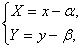
则化为
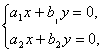
从而变为
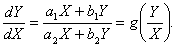
因此,求解上述变量分离方程,最后代回原方程,,即可得到原方程的解.
2. 3常数变易法
一阶线性微分方程
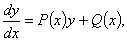
其中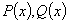 在考虑的区间上是
在考虑的区间上是 的连续函数,若
的连续函数,若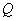
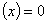 ,变为
,变为

称为一阶齐次线性微分方程,若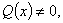 称为一阶非齐次线性微分方程.变易分离方程,易求得它的通解为
称为一阶非齐次线性微分方程.变易分离方程,易求得它的通解为
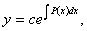
这里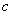 是任意常数.
是任意常数.
现在讨论非齐次线性方程的通解的求法.
不难看出,是的特殊情形,两者既有联系又有差别,因此可以设想它们的解也应该有一定的联系而又有差别,现试图利用方程的通解的形式去求出方程的通解,显然,如果中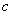 恒保持为常数,它们不可能是的解.可以设想在中将常数
恒保持为常数,它们不可能是的解.可以设想在中将常数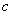 变易为
变易为 的待定函数,使它满足方程,从而求出
的待定函数,使它满足方程,从而求出 为此,令
为此,令

微分之,得到
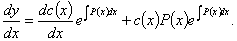
以代入得到
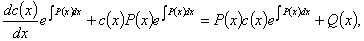
即
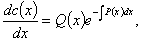
积分后得到
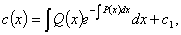
这里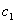 是任意常数.将代入得到
是任意常数.将代入得到
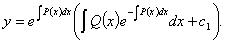
这就是方程的通解.
3.基本方法的应用
3. 1. 一般变量分离应用举例
3.1.1应用举例
例1 求解方程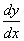
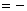
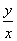
解 将变量分离,得到
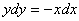
两边积分,即得

因而,通解为

这里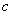 是任意正常数,或者解出
是任意正常数,或者解出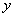 ,写出显函数形式的解
,写出显函数形式的解
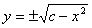
3.1.2应用举例
例2 求解方程
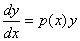
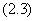
的通解,其中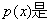
 的连续函数
的连续函数
解 将变量分离,得到
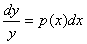
两边积分,即得
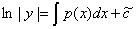
这里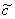 是任意常数。由对数定义,既有
是任意常数。由对数定义,既有
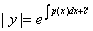 ,
,
即
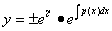
令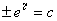 ,得到
,得到
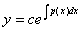
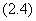
此外, 显然也是方程
显然也是方程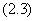 的解,如果允许
的解,如果允许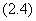 中允许
中允许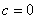 则
则 也就包括在
也就包括在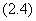 中,因而
中,因而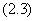 的通解为
的通解为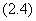 ,其中
,其中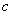 为任意常数。
为任意常数。
3. 2齐次微分方程应用
3.2.1类型一应用举例
例1 求解方程
解 这是齐次微分方程,以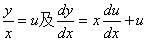 代入,则原方程变为
代入,则原方程变为
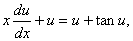
即 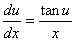
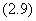
将上式分离变量,既有
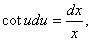
两边积分,得到
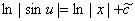
这里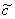 是任意常数,整理后,得到
是任意常数,整理后,得到
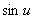 =
=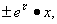
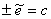 得到
得到
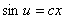
此外,方程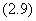 还有解
还有解
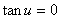
如果在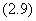 中允许
中允许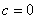 ,则
,则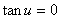 也就包括在
也就包括在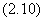 中,这就是说,方程
中,这就是说,方程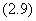 的通解为
的通解为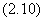
带回原来的变量,得到方程的通解为

3.2.2类型一应用举例
例2 求解方程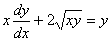 (
(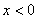 )
)
解 将方程改写为
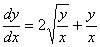
这是齐次微分方程.以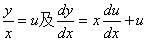 代入,则原方程变为
代入,则原方程变为
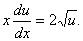
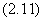
分离变量,得到
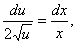
两边积分,得到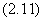 的通解
的通解

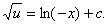
即当 时,
时,
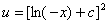
这里c时任意常数.此外,方程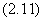 还有解
还有解
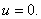
注意,此解并不包括在通解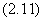 中.
中.
代回原来的变量,即得原方程的通解为
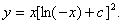 当
当
及 .
.
3.2.3类型二应用举例
例3 求解方程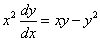 .
.
解 方程可化为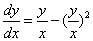 ,令
,令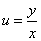 ,将
,将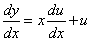 代入上式,
代入上式,
可得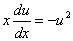 ,易知
,易知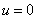 是上式的一个解,从而
是上式的一个解,从而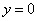 为原方程的一个解.当
为原方程的一个解.当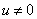 时,分离变量得
时,分离变量得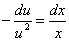 ,两边积分得
,两边积分得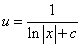 ,故可得原方程的通解为
,故可得原方程的通解为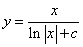 .
.
3.2.4类型二应用举例
例4 求解方程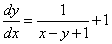 .
.
解 令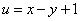 ,则有
,则有
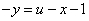 ,
,
代入所求方程
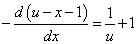 ,
,
整理可得
 ,
,
由变量分离得
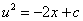 ,
,
故所求方程的解为
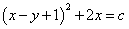 .
.
3. 2. 5类型二应用举例
例5 求解方程
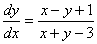
解 解方程组
得 令
令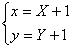
代入上式方程,则有

再令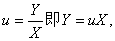 则上式可化为
则上式可化为
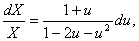

因此

记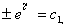 并带回原变量,得
并带回原变量,得
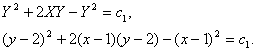
此外容易验证
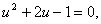
即
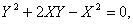
也是方程的解 ,因此方程的通解为

其中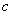 为任意的常数.
为任意的常数.
3. 3利用积分因子求解
例6 求解方程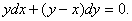
解 这里 方程不是恰当的。
方程不是恰当的。
因为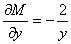 只与
只与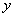 有关,故方程有只与
有关,故方程有只与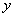 的积分因子
的积分因子
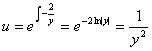
以 乘方程两边,得到
乘方程两边,得到

或者写成
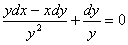
因而通解为

3. 4利用恰当微分方程求解
例7 求解方程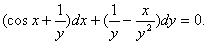
解 因为 ,故方程是恰当微分方程。把方程重新分项组合,得到
,故方程是恰当微分方程。把方程重新分项组合,得到
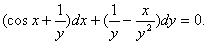 ,
,
即
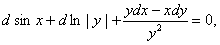
或者写成
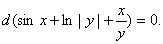
于是,方程的通解为
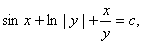
这里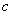 是任意常数
是任意常数
结束语
一阶常微分方程的初等解法是把微分方程的求解问题转化为积分问题,其解的表达式由初等函数或超越函数表示,是常微分方程发展初期数学家的辛勤成果。对于一个给定的常微分方程,不仅要准确判断它属于何种类型,还要注意学习的解题技巧,从中总结经验, ,对各种方法的推导进行分析归纳,并根据方程特点,引进适当的变换,将方程换为能求解的类型.
参考文献
[1] 王高雄,周之铭,朱思铭,王寿松.常微分方程(第三版)[M].北京:高等教育出版社; .
.
[2] 杨继明,常系数线性微分方程组的解法[J];宝鸡文理学院学报(自然科学版);2001.
[3] 伍卓群,李勇编,常微分方程(第三版)[M],北京:高等教育出版社,2004
[4] 杨继明,蔡炯辉;常系数非齐次线性微分方程组初值问题的求解公式[J].宝鸡文理学院学报(自然科学版);20##年01期
第二篇:一阶常微分方程初等解法研究

20xx年6月第3卷 第2期
河套大学学报Jun,2006Vel.3 No.2
一阶常微分方程初等解法研究
刘 林
(巴彦淖尔市蒙古族中学,内蒙古巴彦淖尔市 015000)
[摘 要] 本文在如何引入变换将一阶常微分方程化为变量分离方程方面做了一些探讨并得到了一
些结果。
[关键词] 微分方程;变量代换
[中图分类号]0241.8 [文献标识码]A [文章编号]15-116/C(2006)02-0013-03
1.一阶常微分方程初等解法,就是把常微分方程的求解问题转化为积分问题,能用这种方法求解的微分方程称为可积方程。随着常微分方程在实际生产、,,本文,作为对此问题的一些探索。
11形如h
v(x)]g(x)±v
k
k-1
k
du-f(u))
= 设f(u)≠-k,+v
k-1
k
(y)k,则形如[f(v(x)+h(y)+k]h′
(x)v′(x)h
1-k
k
k
k
dx
(y)f(v(x)+h(y))=0的一
阶方程可化为变量分离方程,其通解为
∫
k
f(u)di=c-kh(y),其中u=v(x)+
kk
(y)h′(y)
k
+f[h(y)dx
±h(y),c为任意常数
k-1
(x)v′(x)=0的方程
例1:解方程
k
定理1 设f≠0,k为常数,则形如
hv
k-1
k-1
2
=(x+y)dx
k
(y)h′(y)+f[h(y)
dx
解:令u=x+y,y=u-x,则
2
-1=udx
du=dx
∫u+1
2
±v(x)]±
(x)v′(x)=0的一阶方程可化为分离变量方
程,其通解为:
v(x)。
k
f(u)
=-kg(x)dx,其中u=h(y)±
∫
k
k
arctanu=x+c,c为任意实数
21形如yf(xy)dx+xg(xy)dy=0的方程
k
证明:令u=h(y)±v(x),于是方程化为:kk
dh(y)+f(u)g(x)+dv(x)=0
kk
k
定理2 f,g为连续函数,则形如
yf(xf)dx+xg(xy)dy=0
的一阶方程可化为变量分离方程,其通解为:
cx=exp
d(h(y)+v(x))+f(u)g(x)=0
kk
du,其中u=xy,C为任
ug(u)-uf(u)
[收稿日期]2006-05-24
[作者简介]刘林(1982-),男,湖南永州人,巴彦淖尔蒙古族中学教师。
?13?

意常数
证明:令xy=u,y=
,则x
dx
2
(1+u)dx=x2-2)xxxu(1+u)dx=xdu-udx
2
f(u)dx+xg(u)-2)=0xdxx(()())
dx=-g(u)du
x
x
=
3
u+2u
u3+2ucx=edx=duxug(u)-uf(u)
x=cyxy+2ddx
=x22
Cx=exp
ug(u)-uf(u)
41形如
2)的方程x
=xf2)dxx
31形如x
2
=f(xy)的方程dx
定理4 f为连续函数,则形如
的一阶方程可化为变量分离方程。其通解为
cx=exp
定理3 f为连续函数,则形如
x=f(xy)dx
2
f(u)-2u2=u,则x的一阶方程可化为变量分离方程,其通解为:
Cx=exp
证明 令
(u)2u=
f(u)-u
2
=
证明:令xy=u,则x)=f(xxduf(xdu(-u)=dx
f(u)-uxcx=exp
f(u)-u
β
fu-2u
cx=exp
f(u)-2u
+
(y)y′=α[1nφ(x)]′51形如h′h(y)αφ-1(x)g(x)fα的方程
φ(x))
定理5 设φ≠0,α为非零常数,则形如
(y)y′=α[1nφ(x)]′φh′h(y)+α
β-1
(x)g(x)fβ为非零常数,则推论 设g≠0,φ≠0,α、形如
(y)y′φ(x)]h′=[1nαβ
g[φ(x)h(y)]
(2.1)
α
β
)α
φ(x)
的一阶方程可化为变量分离方程,其通解为:
()
αdx=φ(x)
,f(u)
(5.1)
其中u=
的一阶方程可化为分离变量方程,其通解为φ(x)c
α
α
φ(x)
,则α
φ(x)
+
=exp
β
,其中u=
u[αg(u)+βf(u)]
证明 令u=
u′=
φ(x)h(y),c为任意常数。
αβ
证明:令u=φ(x)h(y)则有φu′=α
α-1
α-1
h(y)
φ(x)
α2
α
αφ(x)
α
?
(x)φ′(x)h(y)+βφ(x)h
α
β
βαβ-1
(y)?
φ()
h(y)
φ(x)
φ-1+αg(x)fαα
φ(x)φ(x)
=α
φ()
φ(x)]α[1n=[αu+β
φ(x)g[φ(x)h(y)]βu。
g(u)]
f(u)这已是可分离变量的方程,其通解为φ(x)(5.1)
(y)y′=φ6.形如h′
α-1
这是可分离变量的方程,其通解为(2.1)。
22
例2 解方程y(1+xy)dx=xdy
(x)φ′(x)f()
)α
φ(x)
解:令xy=u,则原方程可化为:?14?
的方程
定理6 设φ≠0,α为非零常数,则形如

(y)y′h′=φ
α-1
(x)φ′(x)f)的一阶方α
φ(x)
程可化为分离变量的方程,其通解为
φx=expc意常数.
例3 求解方程x
+2dx
xy=y,(x<0)
这里C为任意常数,此外,方程(1)还有解u=0注意此解不包括在通解(2)中
代回原来得变量,即得原方程的通解
u=[1n(-x)+c],(1n(-x)+c>0)及y=0
2
()
,其中u=α,c为任
f(u)-cuφ(x)
解:将方程改写为齐次方程
=2dx
+,(x<0)xx
以上总结了几类可用变量分离法求解的一阶
常微分方程,其实常微分方程就形式种类而言多不胜举,在涉及具体的常微分方程求解问题时应本着抓住特点、拓宽思路、灵活处理的原则,找出解题的切入点,逐步推进,一举突破。
[参考文献]
[1]汤光宋.常微分方程专题研究[M].华中理工大学出
令
=u,则=x+u,带入原方程得xdxdxx=2udx
(1)
版社.19xx年.
分离变量,得到
=x2u[2]钱祥征.常微分方程解题研究[M].湖南科技出版
社.19xx年.
[3]叶严谦.)[M].高教出版
19xx年.
]、.2
两边积分,得到(1)得通解u=1n(-x)+c即u=[1n(-x)+c],(1n(-x)+c>0)
)
[J19xx年.
ofOne-stepOrdinaryDifferentialEquation
LiuLin
(BayannurMongolianMiddleSchool,BayannurCity,InnerMongolia015000)
Abstract:Thispapermakessomediscussionandgetstosomeconclusiononhowtotransformone-stepOrdi2naryDifferentialEquationintothevariableequationandseparateequation.Keywords:differentialequation;alternation;variableequation
(责任编辑:降毅)
?15?
