第 一 章 一阶微分方程的解法的小结 ⑴、可分离变量的方程:
①、形如 dy
dx?f(x)g(y)
当g(y)?0时,得到dy
g(y)?f(x)dx,两边积分即可得到结果;
当g(?0)?0时,则y(x)??0也是方程的解。
例1.1、dy
dx?xy
解:当y?0时,有
x2dyy?xdx,两边积分得到lny?x22?C(C为常数) 所以y?C1e2(C1为非零常数且C1??e) C
y?0显然是原方程的解; x2
综上所述,原方程的解为y?C1e2(C1为常数)
②、形如M(x)N(y)dx?P(x)Q(y)dy?0
M(x)
P(x)Q(y)N(y)当P(x)N(y)?0时,可有dx?dy,两边积分可得结果;
当N(y0)?0时,y?y0为原方程的解,当P(x0)?0时,x?x0为原方程的解。 例1.2、x(y?1)dx?y(x?1)dy?0
解:当(x?1)(y?1)?0时,有2222y
1?y2dy?xx?1
22dx两边积分得到 lnx?1?lny?1?lnC
2222(C?0),所以有(x?1)(y?1)?C2(C?0); 当(x?1)(y?1)?0时,也是原方程的解;
综上所述,原方程的解为(x?1)(y?1)?C
⑵可化为变量可分离方程的方程: ①、形如dy
dx?g(
y
xyx) dudx?u?g(u)为变量可分离方程,得到22(C为常数)。 解法:令u?,则dy?xdu?udx,代入得到x
f(u,x,C)?0(C为常数)再把u代入得到f(
yx
,x,C)?0(C为常数)。
②、形如
dydx
?G(ax?by),(ab?0)
adx
?dub
解法:令u?ax?by,则dy?得到f(u,x,C)?0
dydx
,代入得到
1dubdx
?
ab
?G(u)为变量可分离方程,
(C为常数)再把u代入得到f(ax?by,x,C)?0
a1x?b1y?c1a2x?b2y?c2
(C为常数)。
③、形如
?f()
解法:10、
a1a2
a1a2
b1b2
?0,转化为
dydx
?G(ax?by),下同①;
2、
?u?x?x0?a1x?b1y?c1?0
?0,?的解为(x0,y0),令?
v?y?yax?by?c?0b2
220?2?b1
a1u?b1va2u?b2v
a1?b1
)?f(
a2?b2
v
)?g(v),下同②;
vuu
得到,
dvdu
?f(
还有几类:yf(xy)dx?xg(xy)dy?0,u?xy
x
2
dydx
?f(xy),v?xy
dydx
?xf(
yx
2
),w?
yx
2
M(x,y)(xdx?ydy)?N(x,y)(xdy?ydx)?0,x?rcos?,y?rsin?
以上都可以化为变量可分离方程。 例2.1、
dydx
?
x?y?5x?y?2
dudx
u?7u
2
解:令u?x?y?2,则dy?dx?du,代入得到1?
u
2
?,有udu??7dx
所以
2
??7x?C
(x?y?2)
(C为常数),把u代入得到?7x?C
2
(C为常数)。
例2.2、
dydx
?
2x?y?1x?2y?1
11??x??u?x????2x?y?1?0?dy?dv33解:由?得到?,令?,有?,代入得到
11x?2y?1?0dx?du???y??v?y?33??
dvdu
?
2u?vu?2v
2??1?21?2t
v
u,令t?v,有dv?tdu?udt,代入得到t?udt?2?t,化简vdu1?2tuudt??
d(1?t?t)2(1?t?t)
22
得到,
duu
?
2?2t?2t
C1?t?t
2
2
,有ln??
13
nl(1?t?t)
2
2
?C(C为常数),
所以有u?
C,(C1??e),故代入得到x?
?
y?
C1
1?
?y?3??3?
1?1x?x??
3?3
1
?
?????
2
,(C1?0)
(3)、一阶线性微分方程:
(x)一般形式:a1
dydx
?a0(x)y?h(x)
标准形式:
dydx
?P(x)y?Q(x)
解法:1、直接带公式:
?P(x)dx?P(x)dx
?P(x)dxQ(x)dx?e??P(x)dx(e?P(x)dxQ(x)dx?C) y?Ce??e?e??
2、积分因子法: y(x)?
1
?(x)
dydx
?P(x)dx [??(x)Q(x)dx?C],?(x)?e
?P(x)y?Q(x),y(x0)?y0
x
3、IVP:
?
x
y?e
?x0P(s)ds
dydx
(?Q(t)e
x0
x
?x0P(s)ds
x
?
dt?y0)?y0e
?x0P(s)ds
t
?
?
x
x0
Q(t)e
?x0P(s)ds
t
dt
例3、(x?1)?ny?e(x?1)dydx
?
nx?1
P(x)dx
n?1
n
解:化简方程为:y?e(x?1),则P(x)??
x
nx?1
,Q(x)?e(x?1);
xn
代入公式得到?(x)?e?
?e
??x?1dx
n
?(x?1)
(C为常数)
-n
所以,y(x)?(x?1)n[?(x?1)?nex(x?1)ndx?C]?(x?1)n(ex?C)(4)、恰当方程:
形如M(x,y)dx?N(x,y)dy?0,?G(x,y),s.t.dG?M(x,y)dx?N(x,y)dy 解法:先判断是否是恰当方程:
如果有
?M(x,y)
?y
?
?N(x,y)?x
恒成立,那么原方程是个恰当方程,找出一个
G(x,y),s.t?G(x,y)
?x?M(X,y),?G(x,y)
?y?N(x,y),
有G(x,y)?C,(C为常数);
例4、(3x2?6xy2)dx?(6x2y?4y3)dy?0
解:由题意得到,M(x,y)?3x2?6xy2,N(x,y)?6x2y?4y3 由?M
?y?12xy??N
?x得到,原方程是一个恰当方程; 下面求一个G(x,y),s.t
?G(x,y)
?x?G(x,y)?x2?M(X,y),?G(x,y)?y3?N(x,y) 由?M(X,y)?3x?6xy得G(x,y)?x?3xy??(y),两边对y求偏222
导得到?G
?y223?6xy???(y)?6xy?4y,得到??(y)?4y,有?(y)?y, 34故G(x,y)?x3?3x2y2?y4,由dG?0,得到
x?3xy?y?C,(C为常数) 3224
(5)、积分因子法:
方程M(x,y)dx?N(x,y)dy?0,??(x,y),s.t.?Mdx??Ndy?0是一个恰当方程那么称?(x,y)是原方程的积分因子;积分因子不唯一。 ?M?N
?x?(x)dx??(x),原方程有只与x有关的积分因子,且为?(x,y)?e?,,①当且仅当?y?
N
两边同乘以?(x,y),化为恰当方程,下同(4)。 ?M?N
?x?(y)dy??(y),原方程有只与y有关的积分因子,且为?(x,y)?e?,②当且仅当?y?
?M
两边同乘以?(x,y),化为恰当方程,下同(4)。
例5.1、(e?3y)dx?2xydy?0 x2
解:由M(x,y)?ex?3y2,N(x,y)?2xy得
?M?y
?
?N?x
?6y?2y?4y
,且有
?M?y
?N
?N?x
??(x)?
2x
3
,有?(x,y)?e
?xdx
2
?x
2
,原方程两边同乘x2,得到
x(e?3y)dx?2xydy?0,化为d((x?2x?2)e?xy)?0,得到解为
(x?2x?2)e?xy?C,(C为常数)
2
x
3
2
2x22x32
例5.2、ydx?(x?y3)dy?0
解:由题意得到,M(x,y)?y,N(x,y)??(x?y3),有
?M?y
??N?x
?1?(?1)?2
?M
有
?y
?
?N?x
??(y)??
2y
?M
,有?(x,y)?e?
2
?(y)dy
?e
??ydy
2
?y
?2
,原方程两边同乘y?2,得
到
dxy
?(?
xy
2
?y)dy?d(
xy
xy
?
y
y
2
2
)?0,得到原方程的解为:
?
2
?C,(C为常数)
(6)、贝努力方程: 形如
dydx
?P(x)y?Q(x)y,
1?n
n
解法:令u?y同(3) 例6、
dydx
?6
?1
,有du?(1?n)y
?n
dy,代入得到
dudx
?(1?n)P(x)u?(1?n)Q(x),下
yx
?xy
?2
2
解:令u?y,有du??ydy,代入得到
dudx
?
6x
u?x,则P(x)?
2
6x
,Q(x)?x,
P(x)dxxC?666
?6,?x,u(x)?x[?x?xdx?C]?有?(x)?e?
8x
(C为常数),把u代入得
到
1y
?
x
2
8
?
Cx
6
,(C为常数).
(7)、一阶隐式微分方程:
一般形式:F(x,y,y?)?0,解不出y?的称为一阶隐式微分方程。
下面介绍四种类型:
(1)y?f(x,y?) (2)x?f(y,y?) (3)F(x,y?)?0 (4)F(y,y?)?0 ①、形如y?f(x,dy
dx
dy
dx), 一般解法:令p?,代入得到y?f(x,p),两边对x求导得到p??f
?x??fdp
?pdx,这是
关于x,p的一阶线性微分方程,仿照(3),
1、得出解为p??(x,C),C为常数,那么原方程的通解为
y?f(x,?(x,C)),C为常数
2、得出解为x??(p,C),C为常数,那么原方程的通解为
x??(p,C)?,C为常数 ??y?f(?(p,C),p)
3、得出解为?(x,p,C)?0,C为常数,那么原方程的通解为
??(x,p,C)?0,C为常数 ??y?f(x,p)
②、形如x?f(y,dy
dx
dy
dx) 一般解法:令p?,代入有x?f(y,p),两边对y求导,得到1
p??f
?y??fdp
?pdy,此方
程是一阶微分方程,可以按照以上(1)—(5)求出通解?(y,p,C)?0,C为常数,那么原方程的通解为
??(y,p,C)?0,C为常数 ?x?f(y,p)?
③、形如F(x,y?)?0
?x??(t)
?y???(t)一般解法:设?
y?,(t为参数),dy?y?dx??(t)??(t)dt,两边积分得到??(t)??(t)dt?C,C为常数,于是有原方程的通解为
?y??
???(t)??(t)dtx??(t)?C,C为常数
④、形如F(y,y?)?0
?y??(t)
?y???(t)一般解法:设?,(t为参数),由关系式dy?y?dx得??(t)dt??(t)dx,有
dx???(t)
?(t)dt,两边积分得到x????(t)
?(t)dt?C,C为常数,于是有
??(t)?x?dt?C??,C为常数 ?(t)?
?y??(t)?
例7.1 xy?3?1?y?
解:令p?y?,得到x?1?p
p3,两边对y求导,得到1p?(1
p3?3(1?p)dp, )4pdy
有dy?(?2
p2?3p)dp,得到y?32p?3
2p2?C,C为常数,于是通解为
1?p?x?3??p,C为常数 ?23?y???C2?p2p?
例7.2 y?y?2ey
解:令p?y?,得到y?p
p?2ep,两边对x求导,得到p?(p?2p)ep2pdpdx,有 dx?(p?2)edp,两边积分得到x?(p?1)e?C,C为常数,于是通解为
?x?(p?1)ep?C,C为常数 ?2py?pe?
例7.3 x?y??1
?x?cost
?y??sintcos2t?1222解:设?,有dy?y?dx?sint?(?sint)dt?
sin2t
4t2dt,所以 y???C,C为常数
于是通解为
sin2tt??y???C
,C为常数 ?42
?x?cost?
例7.4 y2(1?y?2)?1
?y??sint
dy?sint1?dt?
解:设?1,有dx??dt??d(?tant),所以 22
y??ycostsintcost?cost?
x??tant?C,C
于是通解为
x??tant?C??
,C为常数 ?y?1
?cost?
(8)、里卡蒂方程: 一般形式:
dydx
?P(x)y?Q(x)y?R(x)
1z
2
一般解法:先找出一个特解y0(x),那么令y?y0?程得到
dy0dxdzdx?1dzz
2
,有
dydx
?
dy0dx
?
1dzz
2
dx
,代入原方
dx
?P(x)(y0?
1z
)?Q(x)(y0?
2
1z
)?R(x),
化简得到
?(2P(x)y0?Q(x))z?P(x)?0,为一阶线性微分方程,解出
z(x)??(x,C),C为常数
那么原方程的通解为
y?y0?
1
,C为常数
?(x,C)
例8 xy??(xy?2)?0
1x
?
?1x
2
22
解:我们可以找到一个特解y0?令y?
1x?1z
,验证:y0?
2
,代入满足原方程。
1dzz
2
,y???
?2x
1x
2
?
1dzz
2
dx
,代入有x(?
1e?x
2dx
1x
2
?
2
dx
)?(x(
1x
?
1z
)?2)?0,
2
化简得到,
dzdx
z?1,所以有z(x)?
[?e
?xdx
dx?C]?
x3
?
Cx
2
,C为常数
所以原方程的解为
y?
1x?
1x3?Cx
2
,C为常数 或 y?
1x
第二篇:总结一阶常微分方程奇解的求法
总结一阶微分方程奇解的求法
摘要:利用有关奇解的存在定理,总结出求一阶微分方程奇解的几种方法,并通过一些具体的例题说明这几种方法的应用
Using relevant theorems to develop several methods of finding singular solution of ordinary differential equation. In addition, illustrate the application of these methods through the concrete examples.
关键词:常微分方程 奇解 c-判别式 p-判别式
方法一:利用c-判别式求奇解
设一阶微分方程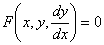 ①
①
可求出方程①的通解为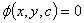 ②
②
如果 ③
③
是微分方程①的解,且对③式满足: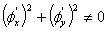 ④
④
则③是微分方程①的奇解,且是通解②的包络。
例1:方程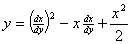 的奇解
的奇解
解:首先,本具题意求出该微分方程的通解为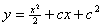 与
与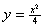
其中c为任意常数
当时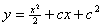 ,
, 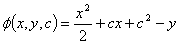
其相应的c-判别式为
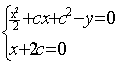
易得到: 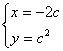
代入原微分方程,可知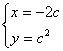 不是原微分方程的解;
不是原微分方程的解;
当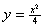 时,易求出
时,易求出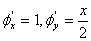 ,则有
,则有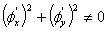
故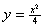 为原微分方程的奇解
为原微分方程的奇解
例2:试求微分方程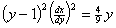 的奇解
的奇解
解:首先,根据题意求出微分方程的通解为: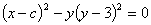
其中c为任意常数
再由相应的c-判别式:
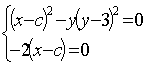
易求出: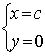 或
或 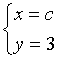
当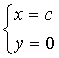 时,代入原微分方程成立;
时,代入原微分方程成立;
所以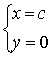 为原微分方程的解
为原微分方程的解
且有 ;
;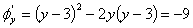
满足(Φ‘x )2+(Φ‘y)2≠0
易验证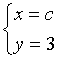 不是原微分方程的解
不是原微分方程的解
故x=c, y=0 是元微分方程的奇解。
方法二:利用p-判别法求奇解
在微分方程①中,设y′=p,则此方程的p-判别式为:
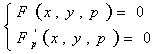 ⑤
⑤
消去p之后得到的函数y=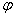 (x)是微分方程①身为解,
(x)是微分方程①身为解,
而且设条件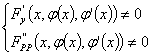 成立,
成立,
则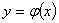 是微分方程①的奇解。
是微分方程①的奇解。
例1:求微分方程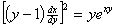 的奇解
的奇解
解:令 ,则原微分方程可化为:
,则原微分方程可化为:
则此微分方程的p-判别式为:
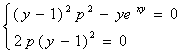
消去p之后得到p-判别式曲线y=0, 易知y=0是原微分方程的解;
但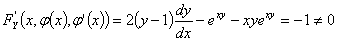
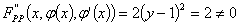
故y=0是原微分方程的奇解
方法三:利用c-判别式和p-判别式共同求奇解
若由③式和⑤式分别得到
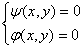 的公共解,则可能是微分方程①的奇解;值得注意的是,此方法用于当c-判别式和p-判别式均易求出时。
的公共解,则可能是微分方程①的奇解;值得注意的是,此方法用于当c-判别式和p-判别式均易求出时。
例:求出微分方程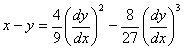 的奇解
的奇解
解:令 ,则原微分方程可化为:
,则原微分方程可化为: 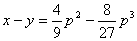
则其p-判别式为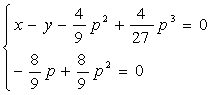
消去p后得到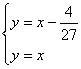
又由原微分方程得到其通解为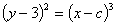
则其c-判别式为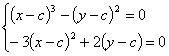
消去c后得到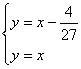
经验证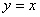 不是微分方程的解,
不是微分方程的解,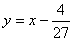 是原微分方程的解;
是原微分方程的解;
所以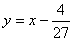 是原微分方程的奇解。
是原微分方程的奇解。
方法四:若易求出微分方程的参数解,且参数不易消去时求奇解的方法
设微分方程①有形如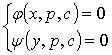 的通解,其中p为参数
的通解,其中p为参数
则奇解可由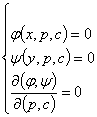 所确定,其中
所确定,其中 为雅克比行列式,
为雅克比行列式,
且要满足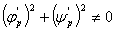
例:求微分方程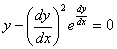 的奇解
的奇解
解:设 ,则原微分方程可化为
,则原微分方程可化为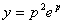
对其两边进行求导,再积分可得:
原微分方程的通解为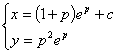
即: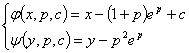
这是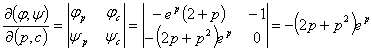
所以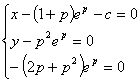
经计算得: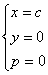 或
或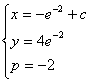
当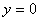 时,
时,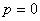 ,易知
,易知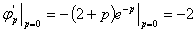
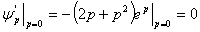
则有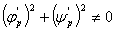
所以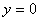 是原微分方程的奇解
是原微分方程的奇解
当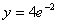 时,
时,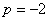 ,易知
,易知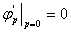 ,
,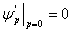 ,
,
故有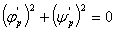
所以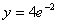 不是原微分方程的奇解
不是原微分方程的奇解
综上所述,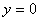 是原微分方程的奇解。
是原微分方程的奇解。
参考文献
[1] 王佩伦,李凤庭,吕延华.常微分方程[M].1版.武汉:武汉大学出版社, 1993:108-110
[2]王高雄,周之铭,朱思铭等.常微分方程[M].3版.北京:高等教育出版社,2006:103-111
[3]丁同仁,李承治.常微分方程教程[M].1版.北京:高等教育出版社,1991:101-113
[4]曾庆健.一类常微分方程奇解的求法[J].安徽电子信息职业技术学院学报,2004,3:234-235
[5]王五生,付美玲,侯宗毅.一阶非线性常微分方程奇解的求法[J].高等数学研究,2010,13(4):65-67

致谢信
光阴似箭,岁月如梭,不知不觉我即将走完大学生涯的第四个年头,回想这一路走来的日子,父母的疼爱关心,老师的悉心教诲,朋友的支持帮助一直陪伴着我,让我渐渐长大,也慢慢走向成熟。
首先,我要衷心感谢一直以来给予我无私帮助和关爱的老师们,特别是我的辅导员XXX老师,指导老师XXX老师,专业课XXX老师、XXX老师、XXX老师,谢谢你们这四年以来对我的关心和照顾,从你们身上,我学会了如何学习,如何工作,如何做人。
其次,我还要真诚地谢谢我的室友和同学,在这四年当中,你们给予了我很多帮助,在我的学习工作生活各个方面,你们给我提出了很多宝贵的建议,我的成长同样离不开你们。同窗的友情同样难忘,芙蓉湖畔、南强灯下,我们一同嬉笑过、拼搏过,这一路与你们同行真好!感谢我所有朋友对我的包容、体谅,谢谢大家
最后,我要感谢我的父母及家人,没有人比你们更爱我,你们对我的关爱让我深深感受到了生活的美好,谢谢你们一直以来给予我的理解、鼓励和支持,你们是我不断取得进步的永恒动力。
也许永远没有那一天,前程如朝霞般绚烂;也许永远没有那一天,成功如灯火般辉煌;也许只能是这样,攀援却达不到顶峰,也许一路走来,只为今天在我毕业论文的最后, 对所有关心帮助我的人说一声:谢谢……
