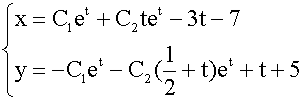常微分方程复习与考试提纲
一、复习与分值结构
总体分三块,解方程部分,包括第2,4,5章,这部分内容分值在60分左右;理论部分,就是,主要是第三章,第四章,第五章等的解的存在唯一性定理以及解的结构定理20分左右;应用部分20分左右; 其次从试题难度上看70左右的基础题、常规题,20分左右的,具有一定灵活性的问题,10左右难题。
二、知识点解析
(一) 解方程部分分一阶、高阶与方程组三部分
1、一阶微分方程:解方程的三个思想:可分离变量类型,全微分(恰当)微分方程,参数方程法
(1)可分离变量类型及其可化为可分离变量类型的方程的类型,这部分习题主要集中在P42-43,P49-50;
a.齐次方程 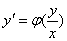 ,令
,令 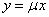 即可;
即可;
b.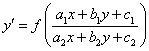 ;
;
c.一些简单的组合变换,如P43,2(1),(2),(5)等;
d.一阶线性微分方程及其通解公式(含伯努利方程,黎卡提方程),见P44-45,其主要思想是常数变异法,其实质是变量分离;特别提示一阶线性微分方程是目前解决的最为彻底的一类方程,应该好好掌握。
(2)全微分(恰当)微分方程及其可化为全微分微分方程的类型,这部分习题主要集中在P60-61;
a.全微分(恰当)微分方程的定义及其判定的充要条件;
b.要求熟记的一些简单二元函数的全微分,见P54及课堂提供;
c.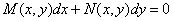 分别具有形为
分别具有形为 、
、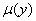 、
、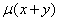 和
和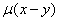 的充要条件及其推导,见P52;
的充要条件及其推导,见P52;
d.方程变换前的积分因子与方程变换前的积分因子之间的关系,P61,5我给大家提供的第二种解法等;
e.常见用到的结论,如P61,4,5,8,11等;
f.难点问题:P61 2(11),10等。
(3) 参数方程法,主要习题见P70,与P73 1 (10)(19)(20)等;
a.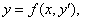 或
或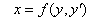 ,可设
,可设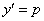 (参数),然后求解;
(参数),然后求解;
b.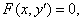 或
或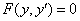 ,视问题而灵活设定。
,视问题而灵活设定。
最后P70-72章节学习要点认真阅读,P72-74 习题认真解答,总结提高。
2、高阶微分方程 主要解法:常数变异法,高阶常系数线性微分方程的待定系数法,Laplas变化法(Laplac变化法本次不作考试内容);
a.基本解组的定义、判定方法及其在解方程中的作用, P126,132 4;
b.Wronsky行列式与刘维尔公式的推导及其应用,P122,P132 5-6;
c.常数变异法解答二阶微分方程的微分方程,P131-132 3;
d.解的结构定理与性质定理,见P125,定理6,P126,性质1-2,定理7,P129,定理8-9;
e.高阶齐次常系数线性微分方程的的解法---待定指数函数法(又名特征根法),欧拉方程的解法,见P164-166;
f.高阶非齐次常系数线性微分方程特解的求法,待定系数法;
g.降阶解方程P166-172,要求掌握基本类型,P182-183 1;
h.幂级数解法这次不做考试要求。
3、线性微分方程组解法,常数变异法,与特征根法
a.解的结构定理与性质定理,见P205,定理6,P211,性质1-2,定理7,P217,7;
b.基解矩阵的定义、性质及其应用求法,Wronsky行列式的定义及刘维尔公式,见P207-2010,定理1*,定理2*,推论1*,推论2*,P217,5,P216,2
c.常数变异法解方程组,理论上很完善,但实际操作主要针对二阶
d.常系数一阶线性微分方程组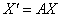 的解法,
的解法,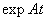 的与一般基解矩阵的求法,见P221,定理9,P227,定理10,P230,公式(5.52)及P231,例题7等,其次见P244-245的习题,尤其上过作业本的习题。
的与一般基解矩阵的求法,见P221,定理9,P227,定理10,P230,公式(5.52)及P231,例题7等,其次见P244-245的习题,尤其上过作业本的习题。
e.利用方程的解的表达式研究解的性质,见P235,定理11。
(二) 理论部分:主要是主要是第三章,第四章,第五章的解的存在唯一性定理以及解的结构定理;
1、 第三章解的存在唯一性定理
a.解的存在唯一性定理的内容,应用与证明的主要方法皮卡尔逼近法以及近似解的求法及误差估计等要求掌握,见P77,定理1,P86,定理2,P87,例题1,P88-89,1-4,9;
b.解的延拓以及解对初值的连续可微性定理要求了解;
c.奇解、包络的定义与求法要求掌握简单类型。
2、 高阶线性微分方程与微分方程组的关系,以及解的存在唯一性定理的内容,解的性质与解的结构性定理及其应用。
(三) 应用部分,内容涉及第1-6章;
1、主要见于把未知其他简单问题转化为常微分方程,然后应用常微分方程理论获得解决,见P43,4-5,P49,1(16),2,P88-89,4,9,P165-166,6-7,P183,5-6,P218,13
2、几何应用,把几何问题转化为微分方程问题,然后获得求解,见P28,6,8(1-5)列微分方程并求解微分方程问题,P74,2。
3、简单的物理问题,以我在这里提及的为准,其余暂不涉及,见P74,3,P41,例题9,P165,6;
4、第六章1-4节中的一些简单的概念问题与奇点、极限环的求解以及稳定性的判定。
三、复习要求:
重点在解方程(60%左右),理论部分要弄清(20%左右),应用部分不能丢(20%)。
要求:1、看书全面复习,平时的作业要彻底理解清楚;2、依据提纲重点复习,根据各自的情况解决弱点,巩固优势部分;3、对照提纲查漏补缺,复习完成。
提示:不管那一份内容,关键都是解题及解题思想的应用,要注意及时总结提高。
最后,祝大家大吉大利!
第二篇:二阶常微分方程解
第七节 二阶常系数线性微分方程的解法
在上节我们已经讨论了二阶线性微分方程解的结构,二阶线性微分方程的求解问题,关键在于如何求二阶齐次方程的通解和非齐次方程的一个特解。本节讨论二阶线性方程的一个特殊类型,即二阶常系数线性微分方程及其求解方法。先讨论二阶常系数线性齐次方程的求解方法。
§7.1 二阶常系数线性齐次方程及其求解方法
设给定一常系数二阶线性齐次方程为
 +p
+p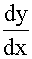 +qy=0 (7.1)
+qy=0 (7.1)
其中p、q是常数,由上节定理二知,要求方程(7.1)的通解,只要求出其任意两个线性无关的特解y1,y2就可以了,下面讨论这样两个特解的求法。
我们先分析方程(7.1)可能具有什么形式的特解,从方程的形式上来看,它的特点是 ,
,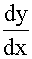 ,y各乘以常数因子后相加等于零,如果能找到一个函数y,其
,y各乘以常数因子后相加等于零,如果能找到一个函数y,其 ,
,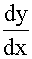 ,y之间只相差一个常数因子,这样的函数有可能是方程(7.1)的特解,在初等函数中,指数函数erx,符合上述要求,于是我们令
,y之间只相差一个常数因子,这样的函数有可能是方程(7.1)的特解,在初等函数中,指数函数erx,符合上述要求,于是我们令
y=erx
(其中r为待定常数)来试解
将y=erx,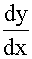 =rerx,
=rerx, =r2erx代入方程(7.1)
=r2erx代入方程(7.1)
得 r2erx+prerx+qerx=0
或 erx(r2+pr+q)=0
因为erx≠0,故得
r2+pr+q=0
由此可见,若r是二次方程
r2+pr+q=0 (7.2)
的根,那么erx就是方程(7.1)的特解,于是方程(7.1)的求解问题,就转化为求代数方程(7.2)的根问题。称(7.2)式为微分方程(7.1)的特征方程。
特征方程(7.2)是一个以r为未知函数的一元二次代数方程。特征方程的两个根r1,r2,称为特征根,由代数知识,特征根r1,r2有三种可能的情况,下面我们分别进行讨论。
(1)若特证方程(7.2)有两个不相等的实根r1,r2,此时er1x,er2x是方程(7.1)的两个特解。
因为 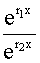 =e
=e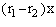 ≠常数
≠常数
所以er1x,er2x为线性无关函数,由解的结构定理知,方程(7.1)的通解为
y=C1er1x+C2er2x
(2)若特征方程(7.2)有两个相等的实根r1=r2,此时p2-4q=0,即
有r1=r2=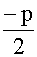 ,这样只能得到方程(7.1)的一个特解y1=er1x,因此,我们还要设法找出另一个满足
,这样只能得到方程(7.1)的一个特解y1=er1x,因此,我们还要设法找出另一个满足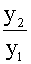 ≠常数,的特解y2,故
≠常数,的特解y2,故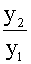 应是x的某个函数,设
应是x的某个函数,设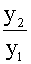 =u,其中u=u(x)为待定函数,即
=u,其中u=u(x)为待定函数,即
y2=uy1=uer1x
对y2求一阶,二阶导数得
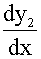 =
= er1x+r1uer1x=(
er1x+r1uer1x=( +r1u)er1x
+r1u)er1x
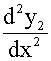 =(r21u+2r1
=(r21u+2r1 +
+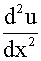 )er1x
)er1x
将它们代入方程(7.1)得
(r21u+2r1 +
+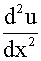 )er1x+p(
)er1x+p( +r1u)er1x+quer1x=0
+r1u)er1x+quer1x=0
或
[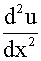 +(2r1+p)
+(2r1+p)  +(r21+pr1+q)u]er1x=0
+(r21+pr1+q)u]er1x=0
因为er1x≠0,且因r1是特征方程的根,故有r21+pr1+q=0,又因r1=-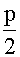 故有2r1+p=0,于是上式成为
故有2r1+p=0,于是上式成为
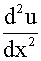 =0
=0
显然满足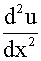 =0的函数很多,我们取其中最简单的一个
=0的函数很多,我们取其中最简单的一个
u(x)=x
则y2=xerx是方程(7.1)的另一个特解,且y1,y2是两个线性无关的函数,所以方程(7.1)的通解是
y=C1er1x+C2xer1x=(C1+C2x)er1x
(3)若特征方程(7.2)有一对共轭复根 r1=α+iβ,r2=α-iβ
此时方程(7.1)有两个特解
y1=e(α+iβ)x y2=e(α-iβ)x
则通解为
y=C1e(α+iβ)x+C2e(α-iβ)x
其中C1,C2为任意常数,但是这种复数形式的解,在应用上不方便。在实际问题中,常常需要实数形式的通解,为此利用欧拉公式
eix=cosx+isinx,e-ix=cosx-isinx
有 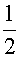 (eix+e-ix)=cosx
(eix+e-ix)=cosx
 (eix-e-ix)=sinx
(eix-e-ix)=sinx
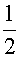 (y1+y2)=
(y1+y2)=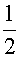 eαx(eiβx+e-iβx)=eαxcosβx
eαx(eiβx+e-iβx)=eαxcosβx
 (y1-y2)=
(y1-y2)= eαx(eiβx-e-iβx)=eαxsinβx
eαx(eiβx-e-iβx)=eαxsinβx
由上节定理一知,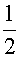 (y1+y2),
(y1+y2), (y1-y2)是方程(7.1)的两个特解,也即eαxcosβx,eαxsinβx是方程(7.1)的两个特解:且它们线性无关,由上节定理二知,方程(7.1)的通解为
(y1-y2)是方程(7.1)的两个特解,也即eαxcosβx,eαxsinβx是方程(7.1)的两个特解:且它们线性无关,由上节定理二知,方程(7.1)的通解为
y=C1eαxcosβx+C2eαxsinβx
或 y=eαx(C1cosβx+C2sinβx)
其中C1,C2为任意常数,至此我们已找到了实数形式的通解,其中α,β分别是特征方程(7.2)复数根的实部和虚部。
综上所述,求二阶常系数线性齐次方程(7.1)的通解,只须先求出其特征方程(7.2)的根,再根据他的三种情况确定其通解,现列表如下

例1. 求下列二阶常系数线性齐次方程的通解
(1)  +3
+3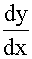 -10y=0
-10y=0
(2)  -4
-4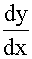 +4y=0
+4y=0
(3)  +4
+4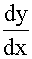 +7y=0
+7y=0
解 (1)特征方程r2+3r-10=0有两个不相等的实根
r1=-5,r2=2
所求方程的通解 y=C1e-5r+C2e2x
(2)特征方程r2-4r+4=0,有两重根
r1=r2=2
所求方程的通解y=(C1+C2x)e2x
(3)特征方程r2+4r+7=0有一对共轭复根
r1=-2+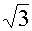 i r2=-2-
i r2=-2-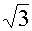 i
i
所求方程的通解 y=e-2x(C1cos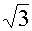 x+C2sin
x+C2sin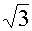 x)
x)
§7.2 二阶常系数线性非齐次方程的解法
由上节线性微分方程的结构定理可知,求二阶常系数线性非齐次方程
 +p
+p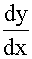 +qy=f(x) (7.3)
+qy=f(x) (7.3)
的通解,只要先求出其对应的齐次方程的通解,再求出其一个特解,而 后相加就得到非齐次方程的通解,而且对应的齐次方程的通解的解法,前面已经解决,因此下面要解决的问题是求方程(7.3)的一个特解。
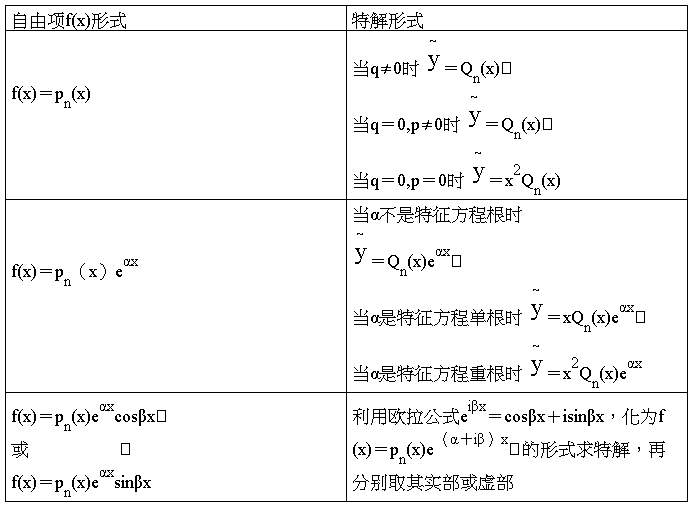
方程(7.3)的特解形式,与方程右边的f(x)有关,这里只就f(x)的两种常见的形式进行讨论。
一、f(x)=pn(x)eαx,其中pn(x)是n次多项式,我们先讨论当α=0时,即当
f(x)=pn(x)时方程
 +p
+p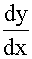 +qy=pn(x) (7.4)
+qy=pn(x) (7.4)
的一个特解。
(1)如果q≠0,我们总可以求得一n次多项式满足此方程,事实上,可设特解 =Qn(x)=a0xn+a1xn-1+…+an,其中a0,a1,…an是待定常数,将
=Qn(x)=a0xn+a1xn-1+…+an,其中a0,a1,…an是待定常数,将 及其导数代入方程(7.4),得方程左右两边都是n次多项式,比较两边x的同次幂系数,就可确定常数a0,a1,…an。
及其导数代入方程(7.4),得方程左右两边都是n次多项式,比较两边x的同次幂系数,就可确定常数a0,a1,…an。
例1. 求 +
+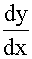 +2y=x2-3的一个特解。
+2y=x2-3的一个特解。
解 自由项f(x)=x2-3是一个二次多项式,又q=2≠0,则可设方程的特解为
 =a0x2+a1x+a2
=a0x2+a1x+a2
求导数 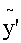 =2a0x+a1
=2a0x+a1
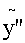 =2a0
=2a0
代入方程有2a0x2+(2a0+2a1)x+(2a0+a1+2a2)=x2-3比较同次幂系数
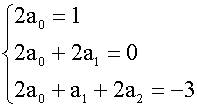 解得
解得 
所以特解 =
=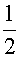 x2-
x2-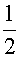 x-
x-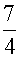
(2)如果q=0,而p≠0,由于多项式求导一次,其次数要降低一次,此时 =Qn(x)不能满足方程,但它可以被一个(n+1)次多项式所满足,此时我们可设
=Qn(x)不能满足方程,但它可以被一个(n+1)次多项式所满足,此时我们可设
 =xQn(x)=a0xn+1+a1xn+…+anx
=xQn(x)=a0xn+1+a1xn+…+anx
代入方程(7.4),比较两边系数,就可确定常数a0,a1,…an。
例2. 求方程 +4
+4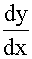 =3x2+2的一个特解。
=3x2+2的一个特解。
解 自由项 f(x)=3x2+2是一个二次多项式,又q=0,p=4≠0,故设特解
 =a0x3+a1x2+a2x
=a0x3+a1x2+a2x
求导数 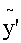 =3a0x2+2a1x+a2
=3a0x2+2a1x+a2
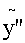 =6a0x+2a1
=6a0x+2a1
代入方程得
12a0x2+(8a1+6a0)x+(2a1+4a2)=3x2+2,比较两边同次幂的系数
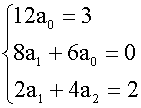 解得
解得 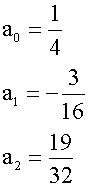
所求方程的特解  =
= x3-
x3- x2+
x2+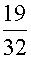 x
x
(3)如果p=0,q=0,则方程变为 =pn(x),此时特解是一个(n+2)次多项式,可设
=pn(x),此时特解是一个(n+2)次多项式,可设
 =x2Qn(x),代入方程求得,也可直接通过两次积分求得。
=x2Qn(x),代入方程求得,也可直接通过两次积分求得。
下面讨论当α≠0时,即当f(x)=pn(x)eαx时方程
 +p
+p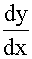 +qy=pn(x)eαx (7.5)
+qy=pn(x)eαx (7.5)
的一个特解的求法,方程(7.5)与方程(7.4)相比,只是其自由项中多了一个指数函数因子eαx,如果能通过变量代换将因子eαx去掉,使得(7.5)化成(7.4)式的形式,问题即可解决,为此设y=ueαx,其中u=u(x)是待定函数,对y=ueαx,求导得
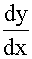 =eαx
=eαx +αueαx
+αueαx
求二阶导数  =eαx
=eαx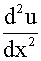 +2αeαx
+2αeαx +α2ueαx
+α2ueαx
代入方程(7.5)得
eαx[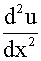 +2α
+2α +α2u]+peαx[
+α2u]+peαx[ +αu]+queαx=pn(x)eαx
+αu]+queαx=pn(x)eαx
消去eαx得
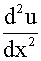 +(2α+p)
+(2α+p)  +(α2+pα+q)u=pn(x) (7.6)
+(α2+pα+q)u=pn(x) (7.6)
由于(7.6)式与(7.4)形式一致,于是按(7.4)的结论有:
(1)如果α2+pα+q≠0,即α不是特征方程r2+pr+q=0的根,则可设(7.6)的特解u=Qn(x),从而可设(7.5)的特解为
 =Qn(x)eαx
=Qn(x)eαx
(2)如果α2+pα+q=0,而2α+p≠0,即α是特征方程r2+pr+q=0的单根,则可设(7.6)的特解u=xQn(x),从而可设(7.5)的特解为
 =xQn(x)eαx
=xQn(x)eαx
(3)如果r2+pα+q=0,且2α+p=0,此时α是特征方程r2+pr+q=0的重根,则可设(7.6)的特解u=x2Qn(x),从而可设(7.5)的特解为
 =x2Qn(x)eαx
=x2Qn(x)eαx
例3. 求下列方程具有什么样形式的特解
(1) +5
+5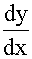 +6y=e3x
+6y=e3x
(2)  +5
+5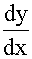 +6y=3xe-2x
+6y=3xe-2x
(3)  +α
+α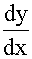 +y=-(3x2+1)e-x
+y=-(3x2+1)e-x
解 (1)因α=3不是特征方程r2+5r+6=0的根,故方程具有形如
 =a0e3x的特解。
=a0e3x的特解。
(2)因α=-2是特征方程r2+5r+6=0的单根,故方程具有形如
 =x(a0x+a1)e-2x的特解。
=x(a0x+a1)e-2x的特解。
(3)因α=-1是特征方程r2+2r+1=0的二重根,所以方程具有形如
 =x2(a0x2+a1x+a2)e-x的特解。
=x2(a0x2+a1x+a2)e-x的特解。
例4. 求方程 +y=(x-2)e3x的通解。
+y=(x-2)e3x的通解。
解 特征方程 r2+1=0
特征根 r=±i得,对应的齐次方程 +y=0的通解为
+y=0的通解为
Y=C1cosx+C2sinx
由于α=3不是特征方程的根,又pn(x)=x-2为一次多项式,令原方程的特解为
 =(a0x+a1)e3x
=(a0x+a1)e3x
此时u=a0x+a1,α=3,p=0,q=1,求u关于x的导数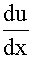 =a0,
=a0,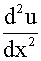 =0,代入
=0,代入
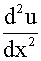 +(2α+p)
+(2α+p) 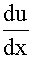 +(α2+αp+q)u=(x-2)得:
+(α2+αp+q)u=(x-2)得:
10a0x+10a1+6a0=x-2
比较两边x的同次幂的系数有
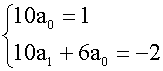 解得 a0=
解得 a0=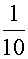 ,a1=-
,a1=-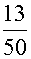
于是,得到原方程的一个特解为
 =(
=(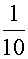 x-
x-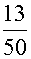 )e3x
)e3x
所以原方程的通解是
y=Y+ =C1cosx+C2sinx+(
=C1cosx+C2sinx+(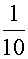 x-
x-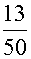 )e3x
)e3x
例5. 求方程 -2
-2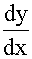 -3y=(x2+1)e-x的通解。
-3y=(x2+1)e-x的通解。
解 特征方程 r2-2r-3=0
特征根 r1=-1,r2=3
所以原方程对应的齐次方程 -2
-2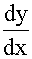 -3y=0的通解Y=C1e-x+C2e3x,由于α=-1是特征方程的单根,又pn(x)=x2+1为二次多项式,令原方程的特解
-3y=0的通解Y=C1e-x+C2e3x,由于α=-1是特征方程的单根,又pn(x)=x2+1为二次多项式,令原方程的特解
 =x(a0x2+a1x+a2)e-x
=x(a0x2+a1x+a2)e-x
此时 u=a0x3+a1x2+a2x,α=-1,p=-2,q=-3
对u关于x求导
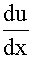 =3a0x2+2a1x+a2
=3a0x2+2a1x+a2
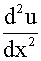 =6a0x+2a1
=6a0x+2a1
代入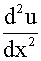 +(2α+p)
+(2α+p) 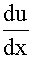 +(α2+pr+q)u=x2+1,得
+(α2+pr+q)u=x2+1,得
-12a0x2+(6a0-8a)x+2a1-4a2=x2+1比较x的同次幂的系数有
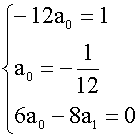 解得
解得 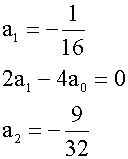
故所求的非齐次方程的一个特解为
 =-
=-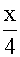 (
(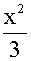 +
+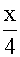 +
+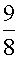 )e-x
)e-x
二、f(x)=pn(x)eαxcosβx或pn(x)eαxsinβx,即求形如
 +p
+p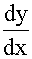 +qy=pn(x)eαxcosβx (7.7)
+qy=pn(x)eαxcosβx (7.7)
 +p
+p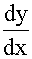 +qy=pn(x)eαxsinβx (7.8)
+qy=pn(x)eαxsinβx (7.8)
这两种方程的特解。
由欧拉公式知道,pn(x)eαxcosβx,pn(x)eαxsinx分别是函数pn(x)e(α+iβ)x的实部和虚部。
我们先考虑方程
 +p
+p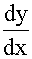 +qy=pn(x)e(α+iβ)x (7.9)
+qy=pn(x)e(α+iβ)x (7.9)
方程(7.9)与方程(7.5)类型相同,而方程(7.5)的特解的求法已在前面讨论。
由上节定理五知道,方程(7.9)的特解的实部就是方程(7.7)的特解,方程(7.9)的特解的虚部就是方程(7.8)的特解。因此,只要先求出方程(7.9)的一个特解,然而取其实部或虚部即可得方程(7.7)或(7.8)的一个特解。
注意到方程(7.9)的指数函数e(α+iβ)x中的α+iβ(β≠0)是复数,而特征方程是实系数的二次方程,所以α+iβ最多只能是它的单根。因此方程(7.9)的特解形为Qn(x)e(α+iβ)x或xQn(x)e(α+iβ)x。
例6. 求方程 -y=excos2x的通解。
-y=excos2x的通解。
解 特征方程 r2-1=0
特征根 r1=1,r2=-1
于是原方程对应的齐次方程的通解为
Y=C1ex+C2e-x
为求原方程的一个特解 。
。
先求方程 -y=e(1+2i)x的一个特解,由于1+2i不是特征方程的根,且pn(x)为零次多项式,故可设u=a0,此时α=(1+2i),p=0,q=-1代入方程
-y=e(1+2i)x的一个特解,由于1+2i不是特征方程的根,且pn(x)为零次多项式,故可设u=a0,此时α=(1+2i),p=0,q=-1代入方程
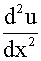 +(2α+p)
+(2α+p) 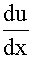 +(α2+αp+q)u=1
+(α2+αp+q)u=1
得[(1+2i)2-1]a0=1 ,即(4i-4)a0=1,得
a0=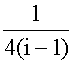 =-
=-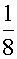 (i+1)
(i+1)
这样得到 -y=e(1+2i)x的一个特解
-y=e(1+2i)x的一个特解
y=-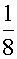 (i+1)e(1+2i)x
(i+1)e(1+2i)x
由欧拉公式
y =-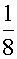 (i+1)e(1+2i)x
(i+1)e(1+2i)x
=-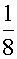 (i+1)ex(cos2x+isin2x)
(i+1)ex(cos2x+isin2x)
=-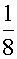 ex[(cos2x-sin2x)+i(cos2x+sin2x)]
ex[(cos2x-sin2x)+i(cos2x+sin2x)]
取其实部得原方程的一个特解
 =-
=-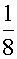 ex(cos2x-sin2x)
ex(cos2x-sin2x)
故原方程的通解为
y=Y+ =C1ex+C2e-x-
=C1ex+C2e-x-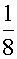 ex(cos2x-sin2x)
ex(cos2x-sin2x)
例7. 求方程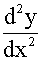 +y=(x-2)e3x+xsinx的通解。
+y=(x-2)e3x+xsinx的通解。
解 由上节定理三,定理四,本题的通解只要分别求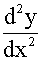 +y=0的特解Y,
+y=0的特解Y,
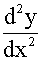 +y=(x-2)e3x的一个特解
+y=(x-2)e3x的一个特解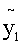 ,
,
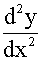 +y=xsinx的一个特解
+y=xsinx的一个特解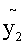
然而相加即可得原方程的通解,由本节例4有
Y=C1cosx+C2sinx,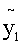 =(
=(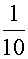 x-
x-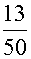 )e3x
)e3x
下面求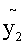 ,为求
,为求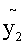 先求方程
先求方程
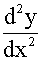 +y=xeix
+y=xeix
由于i是特征方程的单根,且pn(x)=x为一次式,故可设u=x(a0x+a1)=a0x2+a1x,此时α=i,p=0,q=1,对u求导
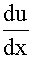 =2a0x+a1,
=2a0x+a1,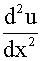 =2a0
=2a0
代入方程
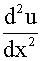 +(2α+p)
+(2α+p) 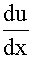 +(α2+pα+q)u=x
+(α2+pα+q)u=x
得 2a0+2i(2a0x+a1)+0=x
即 4ia0x+2ia1+2a0=x
比较x的同次幂的系数有:
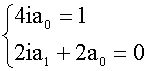 得
得 
即方程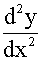 +y=xeix的一个特解
+y=xeix的一个特解
 =(-
=(-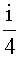 x2+
x2+ x)eix
x)eix
=(-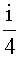 x2+
x2+ )(cosx+isinx)
)(cosx+isinx)
=( x2sinx+
x2sinx+ xcosx)+i(-
xcosx)+i(- x2cosx+
x2cosx+ xsinx)
xsinx)
取其虚部,得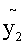 =-
=- x2cosx+
x2cosx+ xsinx
xsinx
所以,所求方程的通解y =Y+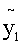 +
+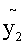
=C1cosx+C2sinx+(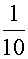 -
-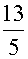 )e3x-
)e3x- x2cosx+
x2cosx+ xsinx
xsinx
综上所述,对于二阶常系数线性非齐次方程
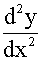 +p
+p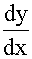 +qy=f(x)
+qy=f(x)
当自由项f(x)为上述所列三种特殊形式时,其特解 可用待定系数法求得,其特解形式列表如下:
可用待定系数法求得,其特解形式列表如下:
以上求二阶常系数线性非齐次方程的特解的方法,当然可以用于一阶,也可以推广到高阶的情况。
例8. 求y+3y″+3y′+y=ex的通解
解 对应的齐次方程的特征方程为
r3+3r2+3r+1=0 r1=r2=r3=-1
所求齐次方程的通解Y=(C1+C2x+C3x2)e-x
由于α=1不是特征方程的根
因此方程的特解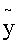 =a0ex代入方程可解得a0=
=a0ex代入方程可解得a0=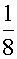
故所求方程的通解为y=Y+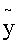 =(C1+C2x+C3x2)e-x+
=(C1+C2x+C3x2)e-x+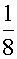 ex。
ex。
§7.3 欧拉方程
下述n阶线性微分方程
a0xn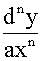 +a1xn-1
+a1xn-1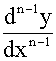 +…+an-1x
+…+an-1x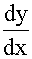 +any=f(x)
+any=f(x)
称为欧拉方程,其中a0,a1,…an都是常数,f(x)是已知函数。欧拉方程可通过变量替换化为常系数线性方程。下面以二阶为例说明。
对于二阶欧拉方程
a0x2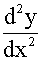 +a1x
+a1x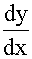 +a2y=f(x) (7.10)
+a2y=f(x) (7.10)
作变量替换令x=et,即t=lnx
引入新变量t,于是有
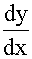 =
=
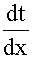 =
=

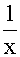 =
=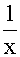

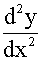 =
=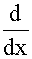 (
(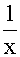
 )=
)=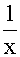
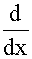 (
( )+
)+
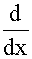 (
(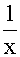 )
)
=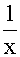

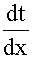 -
-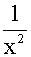

=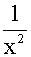
 -
-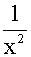

代入方程(7.10)得
a0( -
- )+a2
)+a2 +a1y=f(et)
+a1y=f(et)
即  +
+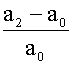
 +
+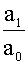 y=
y=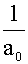 f(et)
f(et)
它是y关于t的常系数线性微分方程。
例9. 求x2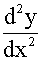 +x
+x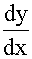 =6lnx-
=6lnx-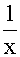 的通解。
的通解。
解 所求方程是二阶欧拉方程
作变换替换,令x=et,则
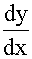 =
=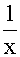
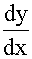
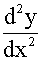 =
=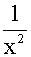
 -
-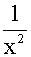

代入原方程,可得
 =6t-e-t
=6t-e-t
两次积分,可求得其通解为
y=C1+C2t+t3-e-t
代回原来变量,得原方程的通解
y=C1+C2lnx+(lnx)3-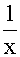
第八节 常系数线性方程组
前面讨论的微分方程所含的未知函数及方程的个数都只有一个,但在实际问题中常遇到含有一个自变量的两个或多个未知函数的常微分方程组。本节只讨论常系数线性方程组,并且用代数的方法将其化为常系数线性方程的求解问题。下面以例说明。
例1. 求方程组
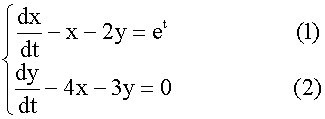 的通解。
的通解。
解 与解二元线性代数方程组中的消元法相类似,我们设法消去一个未知函数,由(1)得
y=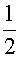 (
(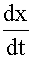 -x-et) (3)
-x-et) (3)
将其代入(2)得
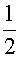 (
( -
-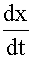 -et)-4x-
-et)-4x-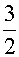 (
(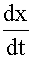 -x-et)=0
-x-et)=0
化简得
 -4
-4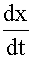 -5x=-2et
-5x=-2et
它是一个二阶常系数非齐次方程
它的通解为 x=C1e5t+C2e-t+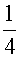 et
et
代入(3)得 y=2C1e5t-C2e-t-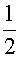 et
et
即所求方程组的通解为

例2. 求解方程组
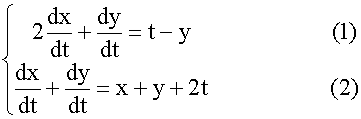 的通解
的通解
解 为消去y,先消去 ,为此将(1)-(2)得
,为此将(1)-(2)得
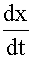 +x+2y+t=0
+x+2y+t=0
即有 y=-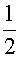 (
(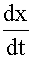 +x+t) (3)
+x+t) (3)
代入(2)得
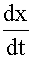 -
-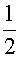
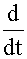 (
(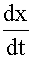 +x+t)-x+
+x+t)-x+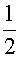 (
(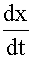 +x+t)-2t=0
+x+t)-2t=0
即  -2
-2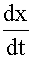 +x=3t-1
+x=3t-1
这是一个二阶常系数线性非齐次方程,解得
x=C1et+C2tet-3t-7
代入(3)得 y=-C1et-C2(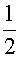 +t)et+t+5
+t)et+t+5
所以原方程组的通解为