第八章 常微分方程
考试内容
常微分方程的基本概念,变量可分离的微分方程 齐次微分方程 一阶线性微分方程 贝努利(Ber-noulli)方程 全微分方程 可用简单变量代换求解的微分方程 可降阶的高微分方程 线性微分方程解的性质及解的结构定理 二姐常系数齐次线性微分方程 高于二阶的某些齐次线性微分方程 简单的二阶常系数非齐次线性微分方程 Euler方程 微分方程的简单应用
考试要求
1. 了解微分方程及其阶,解,通解,初始条件及特解等概念。
2. 掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程。
3. 会解Ber-noulli方程和全微分方程(数二,三不要求),会用简单的变量代换解某些微分方程。
4. 会用降阶法解下列微分方程: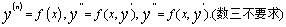
5. 理解线性微分方程解的性质及解的结构定理。
6. 掌握二阶常系数齐次线性微分方程的解法,并会街某限额高于二阶的常系数齐次线性微分方程。
7. 会解自由项多项式,指数函数,正弦函数,余弦函数,以及它们的和与积的二阶常系数非其次线性微分方程。
8. 会解Euler方程(数二,三不要求)。
9. 会用微分方程解决一些简单的应用问题。
重点内容和长常见题型
1. 求五类典型类型的一阶微分方程的通解或特解:这类问题首先是判别方程类型,当然,有些方程不直接而属于我们学过的类型,此时常用的方法是将x与y对调或作适当的变量代换,把原方程化为我们学过的类型;
2. 求解可降阶方程;
3. 求线性常系数齐次和非齐次方程的特解或通解;
4. 根据实际问题或给定的条件建立微分方程并求解;通常是引用物理,力学的定律,几何知识等,运用数学的工具建立微分方程与相应的定解条件(重要)。
5. 综合题,常见的是以下内容的综合:变上限定积分,变积分域的重积分,线积分与路径无关,全微分的充要条件,偏导数等。
8,1 一阶微分方程的类型与解法
一.基本内容
一阶微分方程的一般形式为 其中
其中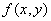 为(x,y)的已知函数,可以缺x或缺y,或者两者都缺。
为(x,y)的已知函数,可以缺x或缺y,或者两者都缺。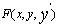 为x,y,
为x,y,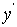 的已知函数,x或y或(x,y)可缺,但必须含有
的已知函数,x或y或(x,y)可缺,但必须含有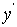 。
。
微分方程的求解:认清类型,按类型求解、一阶微分方程最基本的类型,特征及其解法总结如下:

评注:①在微分方程中不定积分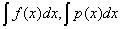 等只表示一个固定的原函数,积分常熟总是另外标出,这是与不定积分不同的习惯。
等只表示一个固定的原函数,积分常熟总是另外标出,这是与不定积分不同的习惯。
②在分离变量方程中,使g(y)=0的点为原方程的特解,在求解过程中不可丢弃。
③对一阶线性微分方程,积分因子法避免了常数变易法的麻烦,又避免记错一阶线性方程解解的公式,希望考生掌握。
通过简单变量代换化为三种基本类型的方程主要有(列表如下)

评注:关于齐次方程的判定采用如下方法较为简便:用tx和ty(t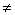 0)代替方程x和y,经过化简方程的形式不变,则方程应判为齐次微分方程。
0)代替方程x和y,经过化简方程的形式不变,则方程应判为齐次微分方程。
二.解题方法,技巧与例题分析
例8,1,1(1994,Ⅲ)填空题:微分方程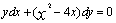 的通解为( )。
的通解为( )。
解:方程为可分离变量方程,变形为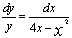 ,两端积分得通解为
,两端积分得通解为
注:一般来说,当y=0时,不能用y来除,所以y-=0是方程的特解,这是在方程求解中应予注意,不过在这里只要允许C=0,特解y=0依然包含在通解之中。》
例8,1,2(1998,1,II)填空题:已知函数y=f(x)在任意点x处的增量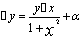 ,且当
,且当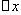
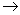 0时,
0时, 的高阶无穷小,y(0)=
的高阶无穷小,y(0)=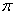 ,则y(1)等于( )。
,则y(1)等于( )。
解:由微分的定义可知: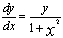 ,这是一个可分离变量方程,注意到y(0)=
,这是一个可分离变量方程,注意到y(0)=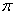 ,解得y(x)=
,解得y(x)= ,因此y(1)=
,因此y(1)= 。
。
例8.1.3(2002,II)已知函数f(x)在(0, )内可导,f(x)>0.
)内可导,f(x)>0. 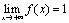 .且满足
.且满足  。求f(x)。
。求f(x)。
解:因为 所以
所以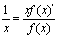 解之得f(x)=C
解之得f(x)=C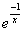 。再由
。再由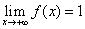 ,可得C=1,因此f(x)=
,可得C=1,因此f(x)=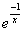 。
。
例8,1,2(2004,II)函数f(x)在 上可导,f(0)=1,且满足等式
上可导,f(0)=1,且满足等式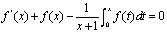 。
。
(1) 求导数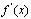 .
.
(2) 证明:当x 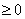 时,成立不等式:
时,成立不等式: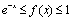 。
。
解:(1)由题设知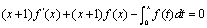 。上式两端关于x求导。得
。上式两端关于x求导。得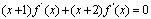 。于是,解上述方程可得:
。于是,解上述方程可得: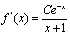 。
。
再由f(0)=1和题中等式可得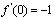 ,因此
,因此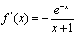 。
。
(3) 由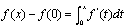 ,可得
,可得 。注意到。当
。注意到。当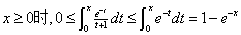 。故知
。故知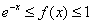 。
。
例8,1,5(1992,1,II)填空题:微分方程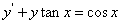 的通解为y=( )
的通解为y=( )
、解:方程为一阶线性方程,用 乘以方程两端,得
乘以方程两端,得 两端积分得
两端积分得 .
.
例8,1,6(1991,Ⅲ)求微分方程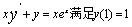 的特解。
的特解。
解:原方程可改写为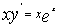 ,因此对方程两端从1到x积分得
,因此对方程两端从1到x积分得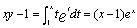 ,故
,故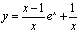 。
。
注:一般的,对求特解问题,先求通解,然后利用定律条件确定通解中的积分常数,但是,在实际计算中,如果直接作定积分,可避免确定定积分常数,直接得到特解。
例8,1,7(1999,Ⅲ)设微分方程 试求在(
试求在(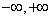 )内连续函数y=y(x),使之在
)内连续函数y=y(x),使之在 内满足方程,且满足条件y(0)=0.
内满足方程,且满足条件y(0)=0.
分析:所给方程为一阶线性非齐次方程。非齐次项为分段函数,故应分段求解。因y(0)=0.应先在 上求解,再注意到y(x)在(
上求解,再注意到y(x)在(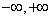 )上连续,即
)上连续,即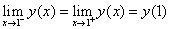 ,即可得到在
,即可得到在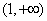 上的解。
上的解。
解:当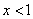 时,有
时,有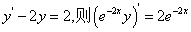 因此由y(0)=0可得
因此由y(0)=0可得 ,因此y(x)在(
,因此y(x)在(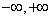 )上连续,所以
)上连续,所以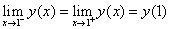 =
=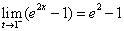 。
。
又当x>1时,有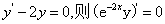 ,故在[1,x]上积分可得
,故在[1,x]上积分可得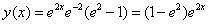 ,故得在(
,故得在(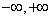 )的连续函数
)的连续函数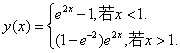
例:8,1,8(1996,Ⅲ)设f(x)为连续函数,
(1) 求初值问题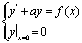 的解y(x),其中a是正常数;
的解y(x),其中a是正常数;
(2) 若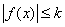 (k为常数),证明当
(k为常数),证明当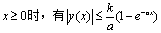 。
。
解:(1)在方程两端同乘 ,得
,得 ,故得
,故得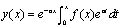
(2)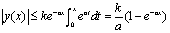 。
。
例8,1,9(1993,1,II)求微分方程 满足初始条件y(1)=1的特解。
满足初始条件y(1)=1的特解。
分析:首先注意到所给的方程为齐次方程,故可按齐次方程的解法求解。又若将方程改写为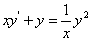 ,可见方程也是Bernoulli方程,因此也可按Bernoulli方程的解法求解。
,可见方程也是Bernoulli方程,因此也可按Bernoulli方程的解法求解。
解①:因方程为齐次方程,令y=xu,方程化为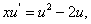 分离变量后,积分得
分离变量后,积分得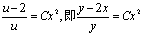 再利用y(1)=1得C=-1,故
再利用y(1)=1得C=-1,故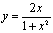 。
。
解②因方程为Bernoulli方程,令 ,解得
,解得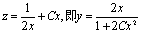 。再利用y(1)=1得C=
。再利用y(1)=1得C=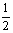 ,故得
,故得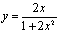
解③:原方程可改写为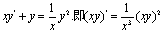 。令u=xy,则
。令u=xy,则 ,解得
,解得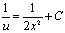 。因此
。因此 。利用
。利用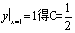 ,故得
,故得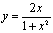 。
。
评注:本题的关键是判别方程的类型,解法③是针对方程的具体特点给出的特殊解法。
例8,1,10(1997,II)求微分方程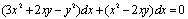 的通解。
的通解。
分析:可以判断此方程既是齐次方程,又是全微分方程,故他有若下几种基本解法。
解①:因方程为齐次方程,令y=xu,方程化为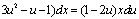 。解得
。解得 ,即
,即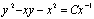

解②:因方程为全微分方程,可采用特殊路径积分法。取(0,0)为起点,(x,y)为终点,可得其通解为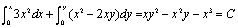 。
。
解③:用凑微分方法求解如下: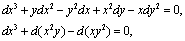 ,所以,方程的通解为
,所以,方程的通解为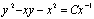 。
。
解④:用不点积分求解如下:设其通解为u(x,y)=C,则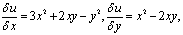 由第一式关于x积分得
由第一式关于x积分得 ,代入第二个式子,得
,代入第二个式子,得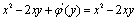 ,由此可得
,由此可得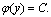 因此原方程的通解为
因此原方程的通解为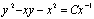
 。
。
评注:对于全微分方程,一般由上述三种解法,通常凑微分法比较简便。
例8,1,11(1994,1,II)设f(x)具有二阶连续导数,f(0)=0,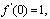 且
且 。为一全微分方程,求f(x)及此微分方程的通解。
。为一全微分方程,求f(x)及此微分方程的通解。
解:由全微分方程的充要条件知 。
。
由f(0)=0.,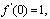 可得
可得
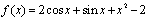 。
。
于是原方程为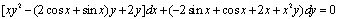 ,其通解为
,其通解为 。
。
例8,1,12(1998,II)设函数f(x)在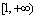 连续,若由曲线y=f(x),直线
连续,若由曲线y=f(x),直线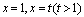 与x轴所围成的平面图形绕x轴旋转一周所成的旋转体体积为
与x轴所围成的平面图形绕x轴旋转一周所成的旋转体体积为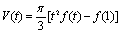 。试求y=f(x)所满足的微分方程,并求该方程满足条件
。试求y=f(x)所满足的微分方程,并求该方程满足条件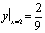 的解。
的解。
解:依题意得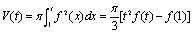 ,即
,即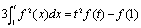 。两边对t求导得
。两边对t求导得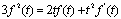 。此方程是Bernoulli方程,也是齐次微分方程。这里采用特殊解法:将方程化为
。此方程是Bernoulli方程,也是齐次微分方程。这里采用特殊解法:将方程化为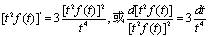 。注意到f(2)=
。注意到f(2)= ,两端关于x从2到x积分可得
,两端关于x从2到x积分可得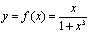 。
。
例8,1,13(2009,Ⅲ)设f(x)是可数函数,且f(x)>0,已知曲线y=f(x)与直线y=0,x=1及x=t(t>1)所围成的曲边梯形绕x轴旋转一周所得的立体的体积是曲边梯行面积值的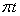 倍,求曲线方程。
倍,求曲线方程。
解:由题设可知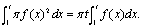 ,两边关于t求导两次可得
,两边关于t求导两次可得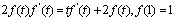 。记y=f(t),则(2y-t)
。记y=f(t),则(2y-t)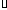
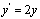 ,即
,即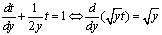 ,于是两边关于y在
,于是两边关于y在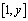 上积分可得
上积分可得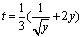 。
。
例8,1,12(2001,II)一个半球体的雪堆,其体积融化的速度与半球面面积S成正比,比例系数为K>0.假设在融化过程中雪堆始终保持半球体状,已知半径为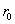 的雪堆在开始融化的3小时内,融化了其体积的
的雪堆在开始融化的3小时内,融化了其体积的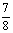 ,问雪堆全部融化需要多少时间?
,问雪堆全部融化需要多少时间?
解:设雪堆在时刻t的体积V= ,侧面积
,侧面积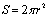 ,由题设知
,由题设知
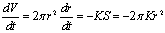 ,于是
,于是
积分得r=-Kt+C,又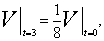 即
即 ,这样K=
,这样K=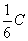 ,从而r=C-
,从而r=C-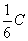 t 。因雪堆全部融化时r=0,故得t=6,即雪堆全部融化需六小时。
t 。因雪堆全部融化时r=0,故得t=6,即雪堆全部融化需六小时。
例8.1.15(1998,I,II)从船上向海中沉放探测仪器,安探测要求,需确定仪器的下沉速度y(从海平面算起)与下沉速度v之间的函数关系,设仪器在重力的作用下,从海平面由静止开始铅直下沉,在下沉过程中还受到阻力与浮力的作用,设仪器的质量为m,体积为B,海水比重为ρ,仪器所受的阻力与下沉速度成正比,比例系数为k(k)0)。试建立y与v所满足的微分方程,并求出函数关系式y=y(v)。
解:取沉放点为坐标原点o,oy轴正向铅直向下,则由牛顿第二定律得 ,将
,将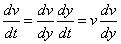 代入消去t,得v与y之间的微分方程
代入消去t,得v与y之间的微分方程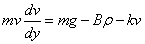 。 分离变量,积分得
。 分离变量,积分得 。由初始条件
。由初始条件 =0定出常数C,可得所求函数关系式为
=0定出常数C,可得所求函数关系式为 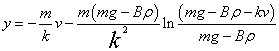 。
。
例;8.1.16(2000,II)某湖泊的水量为V,每年排入湖泊内含污物A的污水量为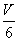 ,流入湖泊内不含A的水量为
,流入湖泊内不含A的水量为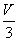 ,已知1999年底湖中A的含水量为5
,已知1999年底湖中A的含水量为5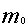 ,超过国家固定指标。为了治理污染,从20##年初起,限定排入湖泊中含A污水的浓度不超过
,超过国家固定指标。为了治理污染,从20##年初起,限定排入湖泊中含A污水的浓度不超过 ,问至少需经过多少年,湖泊中污染物A的含量可降至
,问至少需经过多少年,湖泊中污染物A的含量可降至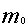 以内?(设湖水中A的浓度时均匀的)
以内?(设湖水中A的浓度时均匀的)
解:设从20##年初(令此时t=0)开始,第t年湖泊中污染物A的总量为m,浓度为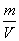 ,则在时间段【t,t+dt】内,排入湖泊中A的量为
,则在时间段【t,t+dt】内,排入湖泊中A的量为 ,流出湖泊的水中A的量为
,流出湖泊的水中A的量为 ,因而在此时间段内湖泊中污染物A的改变量为
,因而在此时间段内湖泊中污染物A的改变量为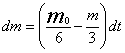 。注意到
。注意到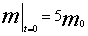 ,可得
,可得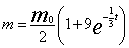 ,令
,令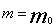 ,得t=6ln3,即至少经过6ln3 年,湖泊中污染物A的含量降至
,得t=6ln3,即至少经过6ln3 年,湖泊中污染物A的含量降至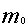 以内。
以内。
8.2 可降阶的高阶微分方程及其解法
一.基本内容
可降阶的微分方程主要有三种,其特征和解法总结如下:
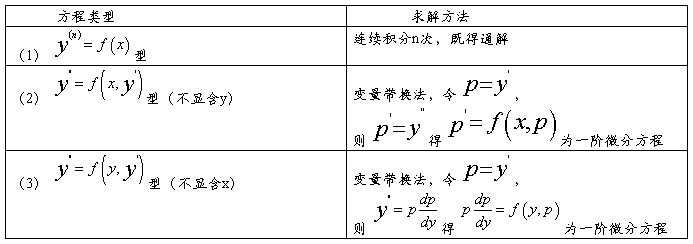
二.解题方法,技巧与例题分析
例 8.2.1(2007,II) 求微分方程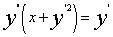 满足初始条件y(1)=
满足初始条件y(1)= (1)=1的特解。
(1)=1的特解。
解:令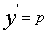 ,则
,则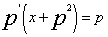 ,于是
,于是
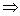
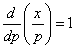 ,注意到x=1时p=1,所以
,注意到x=1时p=1,所以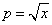 ,因此
,因此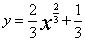
例8.2.2(1991,I,II)在上半平面求一条向上凹的曲线,其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点),且曲线在点(1,1)处的切线与x轴平行。
解:曲线y=y(x)在P(x,y)处的法线方程是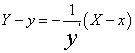 (
(
 )。它与x轴的交点是(x +y
)。它与x轴的交点是(x +y ,0),从而P点到x轴的法线段PQ的长度是
,0),从而P点到x轴的法线段PQ的长度是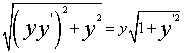 ,
, =0也满足上式。根据题意得微分方程
=0也满足上式。根据题意得微分方程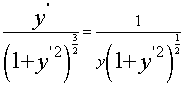 ,即
,即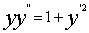 ,且当x=1时,y=1,
,且当x=1时,y=1,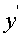 =0.令
=0.令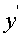 =p,则
=p,则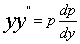 ,代入方程,得
,代入方程,得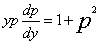 , 或
, 或 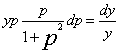 。
。
两端积分并注意到y=1时,p=0,即得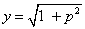 ,于是有
,于是有 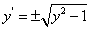 或
或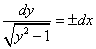 ,积分上式,并注意到x=1时,y=1得
,积分上式,并注意到x=1时,y=1得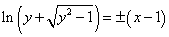 ,因此,所求的曲线方程为
,因此,所求的曲线方程为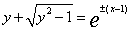 ,即
,即 。
。
注:将 代回原方程可得
代回原方程可得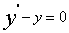 ,从而
,从而 再由y(1)=1,
再由y(1)=1,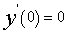 可得
可得 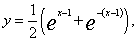 。
。
例 8.2.3(2002,I,II)填空题:微分方程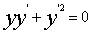 满足条件
满足条件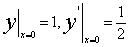 的特解是( )
的特解是( )
解:原方程可化为 ,两端关于x从0到x积分得
,两端关于x从0到x积分得  即
即 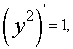 两端再对x从0到x积分得
两端再对x从0到x积分得 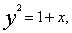
评注:此题属于类型(3)的可降介微分方程,但按一般解法比较复杂,根据方程的特殊结构给出的上述解法比较简单。
例8.2.4(1996,I,II)设对任意 x.>0 ,曲线 y=f(x)上点(x,f(x))处的切线在y轴上的截距等于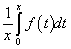 .求f(x)的一般表达式。
.求f(x)的一般表达式。
解:曲线y=f(x)上点(x,f(x))处的切线方程为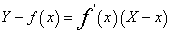 . 令X=0,得截距
. 令X=0,得截距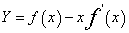 。由题意知
。由题意知 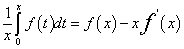 ,即
,即 。上式对x求导,化简得
。上式对x求导,化简得  ,积分得
,积分得 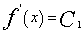 ,因此
,因此 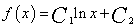 .
.
 例:8.2.5(1999,I,II)设函数y(x)(x》0)二阶可导且
例:8.2.5(1999,I,II)设函数y(x)(x》0)二阶可导且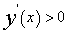 , y(0)=1,过曲线y=y(x)上任意一点P(x,y)作该曲线的切线即x轴的垂线,上述两直线与x轴所围成的三角形的面积即为
, y(0)=1,过曲线y=y(x)上任意一点P(x,y)作该曲线的切线即x轴的垂线,上述两直线与x轴所围成的三角形的面积即为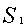 ,区间【0.x】上以y=y(x)为曲边的曲边梯形面积记为
,区间【0.x】上以y=y(x)为曲边的曲边梯形面积记为 ,并设
,并设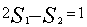 ,求此曲线的y=y(x)的方程。
,求此曲线的y=y(x)的方程。
解:
曲线y=y(x)上点(x,y)处的切线方程为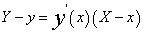 。它与x轴的交点为
。它与x轴的交点为 ,由于
,由于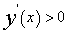 , y(0)=1,从而y(x)>0,于是
, y(0)=1,从而y(x)>0,于是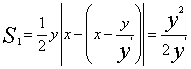 又
又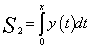 ,故
,故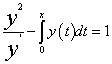 两边对x求导并简化得
两边对x求导并简化得 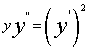 ,
,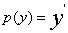 则上述方程可化为
则上述方程可化为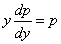 解之得
解之得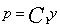 于是
于是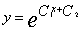 。注意到y(0)=1,
。注意到y(0)=1,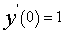 ,可得
,可得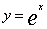 。
。
例:8.2.6(1993.I,II)设物体A从(0,1)出发,以速度大小为常数v沿y轴正向运动,物体B从点(-1,0)与A同时出发,其速度大小为2v方向始终指向A,势建立物体B的运动轨迹所满足的微分方程,并写出初始条件。
解: 轨迹如图所示。设在时刻t,B位于点(x,y)处,则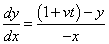 ,两边对x求导得
,两边对x求导得 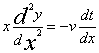 。由于
。由于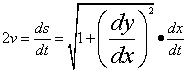 ,
, , 所以,要求的微分方程为
, 所以,要求的微分方程为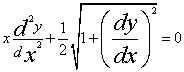 ,其初始条件为
,其初始条件为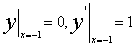 。
。
注:由方程和初始条件可以得到物体B的运动轨迹方程,作为习题。
8.3 线性微分方程解的结构
一.基本内容
这里只限于讨论二阶线性方程,其结论可推广到高阶的线性方程,二阶线性方程的一般形式为 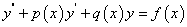 (1)
(1)
当f(x)=0时,有
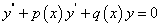 (2)
(2)
称之为与(1)对应的二阶线性齐次方程,同时称(1)为二阶线性非齐次方程。
1.如果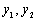 是齐次方程(2)的特解,则其线性组合
是齐次方程(2)的特解,则其线性组合
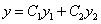 (
(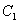 ,
, 是任意常数)
是任意常数)
仍是方程(2)的解,特别地,当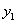 和
和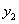 线性无关时,
线性无关时,
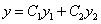 (
(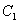 ,
, 是任意常数)
是任意常数)
是方程(2)的通解。
2.如果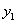 ,
,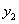 是非齐次方程(1)的两个解,则
是非齐次方程(1)的两个解,则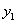 -
-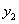 是齐次方程(2)的解。
是齐次方程(2)的解。
3.设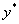 是非齐次方程(1)的一个特解,Y是齐次方程(2)的通解,则y=Y+
是非齐次方程(1)的一个特解,Y是齐次方程(2)的通解,则y=Y+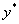 是非齐次方程(1)的通解
是非齐次方程(1)的通解
4.设方程(1)中,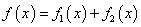 ,而y
,而y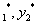 分别是方程
分别是方程
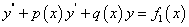 与
与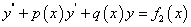
的特解,则 就是方程
就是方程

的特解。
注:结论2,3和4对一阶线性微分方程也成立。
对于二阶常系数齐次线性方程
 (p,q为常数) (3)
(p,q为常数) (3)
称代数方程
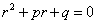
为方程(3)的特征方程,特征方程的解称为方程(3)的特征根。由特征根可得方程(3)通解的结构如下表:

注:对高阶线性常系数齐次微分方程有类似的通解结构。
二.解题方法,技巧与例题分析
例 8.3.1(1995,III)设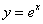 是微分方程
是微分方程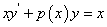 的一个解,求此微分方程满足条件
的一个解,求此微分方程满足条件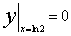 的特解。
的特解。
解:以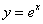 代入原方程,得
代入原方程,得 ,解出
,解出 ,将p(x)代入原方程得
,将p(x)代入原方程得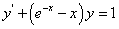 。
。
由于 是方程的一个特解,所以只需解其对齐次方程
是方程的一个特解,所以只需解其对齐次方程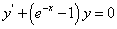 的解。将齐次方程分离变量,并积分得
的解。将齐次方程分离变量,并积分得
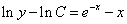 ,
,
即齐次方程的通解为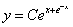 ,所以,原方程的通解为
,所以,原方程的通解为
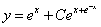
把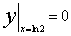 代入,得
代入,得 ,故所求特解为
,故所求特解为
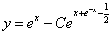 。
。
例 8,3,2(1989,I,II)选择题:设线性无关的函数 都是二阶非齐次线性方程
都是二阶非齐次线性方程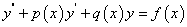 的解,
的解, 是任意常数,则该非齐次线性方程的通解是【】
是任意常数,则该非齐次线性方程的通解是【】
(A)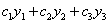 (B)
(B)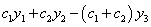
(C ) 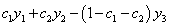 (D)
(D)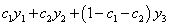
分析:根据线性方程解的结构定理知,对本题中的二阶线性方程,非齐次方程的通解为 ,其中
,其中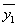 和
和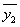 是对应的齐次方程的两个线性无关的特解,
是对应的齐次方程的两个线性无关的特解,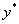 是非齐次方程的特解,又由于非齐次方程两个解之差事齐次方程的一个解,由此很快求出
是非齐次方程的特解,又由于非齐次方程两个解之差事齐次方程的一个解,由此很快求出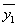 和
和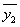 。
。
解:由题设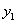 -
- 和
和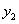 -
- 是对应齐次方程的两个解,且
是对应齐次方程的两个解,且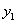 -
- 与
与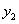 -
- 线性无关。事实上,若令
线性无关。事实上,若令
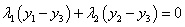 ,
,
则 
由 线性无关,则必有
线性无关,则必有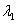 =
= =0,因此
=0,因此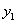 -
- 与
与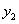 -
- 线性无关。从而
线性无关。从而
y=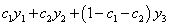
是原方程的通解。故应选(D)。
例 8.3.3 (1997,II)已知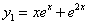 ,
,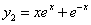 ,
, 是某二阶线性非齐次微分方程的三个解,求此微分方程。
是某二阶线性非齐次微分方程的三个解,求此微分方程。
解①:由线性微分方程解的结构定理知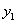 -
- =
=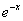 ,
, 为相应齐次微分方程的特解。因此,相应齐次方程有两个线性无关解
为相应齐次微分方程的特解。因此,相应齐次方程有两个线性无关解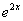 与
与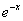 ,
, 是线性非齐次方程的一个特解,故
是线性非齐次方程的一个特解,故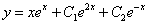 是所求非齐次方程的童鞋,从而有
是所求非齐次方程的童鞋,从而有
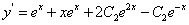 ,
,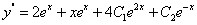 ,
,
消去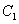 ,
, ,得所求方程为
,得所求方程为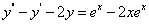 。
。
解②:由线性微分方程解的结构定理知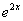 与
与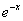 是相应齐次方程的两个无关解,
是相应齐次方程的两个无关解, 是线性非齐次方程的一个特解,故可设此方程为
是线性非齐次方程的一个特解,故可设此方程为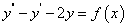 。
。
将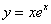 代入,得
代入,得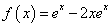 。因此所求方程为
。因此所求方程为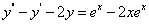 。
。
例 8.3.4(2000,II)选择题:具有特解 的三阶常系数线性微分方程是【】
的三阶常系数线性微分方程是【】
(A)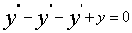 (B)
(B)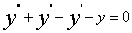
(C ) 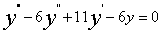 ( D)
( D) 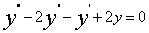
解:甴题设知r=-1,-1,1 为所求齐次线性微分方程对应特征方程的三个根,而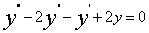 ,故应选(B).
,故应选(B).
评注:此题的另一种解法是,由条件知所求方程的通解为 ,然后通过消去
,然后通过消去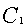 ,
,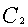 ,
, 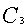 得所求方程。
得所求方程。
例: 8.3.5(2001,I) 填空题:设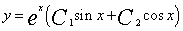 (
(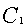 ,
,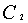 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为()
为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为()
解:由题设可知方程特征根为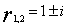 ,则其特征方程为
,则其特征方程为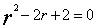 ,故所求方程为
,故所求方程为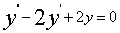 。
。
评注:此题可先求出 ,
,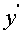 ,然后消去
,然后消去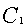 和
和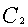 得出方程。
得出方程。
8.4高阶微分方程的解法
一.基本内容
1.二阶常系数线性微分方程的解法
二阶常系数微分方程
 , (p,q为常数)
, (p,q为常数)
当f(x)=0时,其解可由特征方程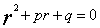 的根和解的结构定理直接得到。
的根和解的结构定理直接得到。
当f(x)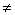 0时,其解法为:
0时,其解法为: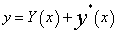 ,其中
,其中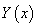 为对应齐次方程通解,
为对应齐次方程通解, 为非齐次方程的一个特解。对某些特殊的非齐次项f(x),特解
为非齐次方程的一个特解。对某些特殊的非齐次项f(x),特解 可用待定系数法求出,它的形式如下:
可用待定系数法求出,它的形式如下:

其中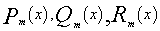 表示x的m次多项式。
表示x的m次多项式。
评注:由韦达公式可知特征方程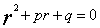 的根
的根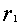 和
和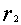 满足
满足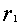 +
+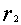 =-q ,
=-q , 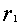
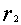 =q。因此方程
=q。因此方程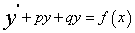 可以改写为
可以改写为 ,即
,即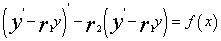 。若令u(x)=
。若令u(x)=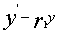 ,则二阶常系数非齐次方程可化为方程组,
,则二阶常系数非齐次方程可化为方程组,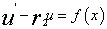 ,
,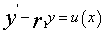 ,进行求解。
,进行求解。
2.Euler方程的解法
形如 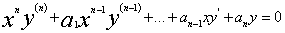 ,(x)0)
,(x)0)
的方程称为Euler方程,它的解法是做变换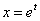 或
或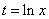 ,即将自变量换位t,则有
,即将自变量换位t,则有
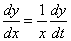
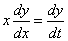
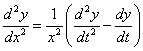
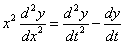
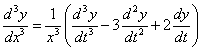
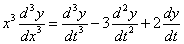
… … …
将这些关系式代入Euler方程,就换为n阶常系数线性方程,从而可利用n阶常系数线性方程的结构得到它的解。
二.解题方法,技巧与例题分析
例 8.4.1(1993,III)设二阶常系数线性微分方程
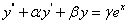
的一个特解为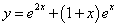 。试确定常数
。试确定常数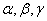 ,并求该方程的通解。
,并求该方程的通解。
解:由题设知原方程的特征根为1和2,所以特征方程为(r-1)(r-2)=0,即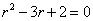 ,故知
,故知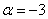 ,
,
为确定 ,只需将特解
,只需将特解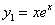 代入方程,得
代入方程,得 ,由此可知
,由此可知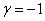 ,从而原方程的通解为
,从而原方程的通解为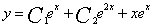 .
.
评注:本题也可将特解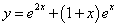 代入原方程,比较方程两端同类项的系数求出
代入原方程,比较方程两端同类项的系数求出
例 8.4.2(1987,I)求微分方程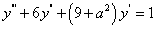 的通解。
的通解。
解:该方程对应的七次方程的特征方程为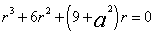 ,其根为
,其根为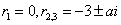 ,则齐次方程的通解为
,则齐次方程的通解为
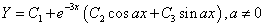 时;
时;
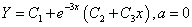 时。
时。
由于r=0为特征方程的单根,则可设非齐次方程的特解为
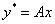 ,
,
代入原方程得 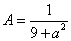
故原方程的特解为
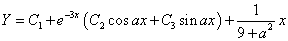 ,
,  时;
时;
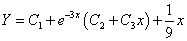 , a=0时
, a=0时
注:此题可令u= 变为二阶线性常系数方程进行求解。
变为二阶线性常系数方程进行求解。
例 8.4.3(1998,I)设函数y=f(x)满足微分方程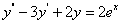 ,且其图形在点(0,1)处的切线与曲线
,且其图形在点(0,1)处的切线与曲线 在该点的切线重合,求函数f(x)。
在该点的切线重合,求函数f(x)。
解①:本题所给方程对应的齐次方程的特征方程为
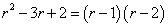 =0,
=0,
其根为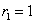 ,
,
则齐次方程的通解为 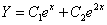 ,
,
由于r=1为特征方程的单根,则可设非齐次方程的特解为
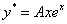
代入原方程 A=-2 ,
故原方程的通解为
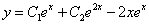 。
。
由题设曲线 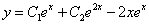 与
与 在点(0,1)处的切线重合可知,y(0)=1,
在点(0,1)处的切线重合可知,y(0)=1, 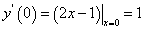 ,则有
,则有
1=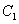 +
+  , -1=
, -1= 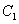 +2
+2 -2,
-2,
解之得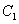 =1,
=1, ,故所求的解为
,故所求的解为
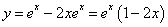 。
。
解②:令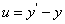 ,则得
,则得
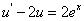
解得  ,
,
因此
 ,
,
解得 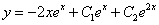
以下过程同解法①。
例:8.4.4(1991,III)求微分方程 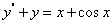 的通解。
的通解。
解:由于方程的特征方程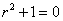 ,特征根为
,特征根为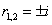 ,故知原方程对应的齐次方程的通解为
,故知原方程对应的齐次方程的通解为 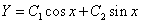
设非齐次方程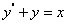 的特解为
的特解为 =Ax+B,代入方程得A=1,B=0,所以
=Ax+B,代入方程得A=1,B=0,所以 =x。
=x。
设非齐次方程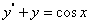 的特解为
的特解为 ,代入方程得E=0,D=
,代入方程得E=0,D=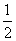 ,所以
,所以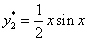
因此原方程的通解为
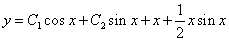
例 8.4.5(1998 ,II)利用代换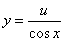 将方程
将方程
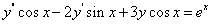 化简,并求出原方程的通解。
化简,并求出原方程的通解。
解:由 u=ycosx 两端对x求导,得
 ,
, 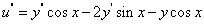 。
。
于是 原方程化为 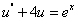 ,
,
其 通解为 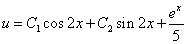 。
。
从而原方程的通解 为
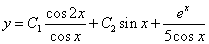 。
。
例 8.4.6 (2003,I,II)设函数y=y(x)在(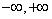 )内具有二阶导数,且
)内具有二阶导数,且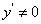 ,x=x(y)是
,x=x(y)是
y=y(x)的反函数。
(1)试讲x=x(y)所满足的微分方程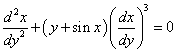 变换为y=y(x)满足的微分方程;
变换为y=y(x)满足的微分方程;
(2)将变换后的微分方程满足初始条件 y(0)=0,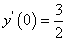 的解
的解
解:(1)由反函数导数公式 可知
可知
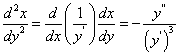 ,
,
代入原方程得
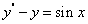 (*)
(*)
设方程(*)的特解为y*=A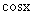 +B
+B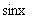 ,代入方程(*)求得A=0,B=-
,代入方程(*)求得A=0,B=-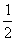 ,故y*=-
,故y*=-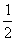
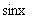 ,从而
,从而 的通解是
的通解是
y(x)=C1ex+C2e-x-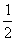
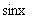
由y(0)=0,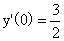 ,得C1=1,C2=-1,故所求初值问题的解为
,得C1=1,C2=-1,故所求初值问题的解为
y(x)=ex-e-x-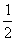
补 充 习 题
1.填空题:
⑴(2005,III,IV)微分方程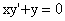 满足初始条件y⑴=2的特解为_
满足初始条件y⑴=2的特解为_
⑵(2005,I,II)微分方程 满足初始条件
满足初始条件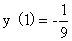 的特解为_
的特解为_
⑶(1996,III)微分方程 的通解为_
的通解为_
⑷(1995,III)微分方程 的通解为_
的通解为_
⑸(1996,I,II)微分方程
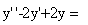 ex通解为_
ex通解为_
⑹(1999,I,II)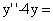 e2x的通解为_
e2x的通解为_
⑺(2004,I)欧拉方程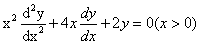 的通解为_
的通解为_
⑻(2007,I,II)二阶常系数非齐次线性微分方程 的通解为_
的通解为_
⑼(2007,III,IV)微分方程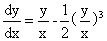 满足
满足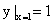 的特解为_
的特解为_
⑽(2000,I)微分方程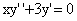 的通解为_
的通解为_
⑾(2009,I)若二阶常系数线性齐次微分方程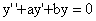 的通解为
的通解为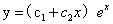 ,则非齐次方程
,则非齐次方程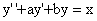 满足条件
满足条件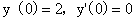 的解为y=_
的解为y=_
⑿(2011,I,II)微分方程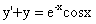 满足条件
满足条件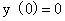 的解为y=_
的解为y=_
⒀(2012,II)微分方程 满足条件
满足条件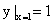 的解为_
的解为_
2.选择题:(在每小题给出的四个选项中,只有一个是符合题目要求的,把所选项前的字母填在题后的括号内)
(1)(2013,II)已知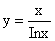 是微分方程
是微分方程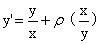 的解,则
的解,则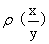 的表达式为
的表达式为
(A)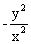 (B)
(B)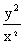 (C)
(C)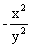 (D)
(D)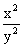
 【 】
【 】
(2)(2011,II)微分方程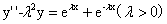 的特解形式为
的特解形式为
(A) (B)
(B)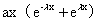
(C)x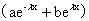 (D)
(D)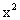
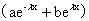 【 】
【 】
3.(1992,III)求微分方程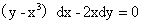 的通解
的通解
4.(1991,IV)求微分方程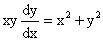 满足条件
满足条件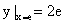 的特解
的特解
5.(1993,III)求微分方程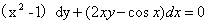 满足初始条件
满足初始条件 的特解
的特解
6.(1999,II)求初值问题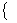
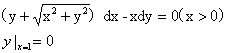 的解
的解
7.(1996,IV)求微分方程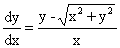 的通解
的通解
8.(1990,II)求微分方程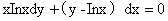 满足条件
满足条件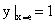 的特解
的特解
9.(2003,III)设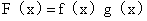 ,其中函数
,其中函数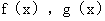 在
在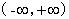 内满足以下条件:
内满足以下条件:

(1)求F(x)所满足的一阶微分方程;
(2)求出F(x)的表达式。
10.(1998,II)设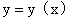 是一向上凸的连续曲线,其上任意一点(x,y)的曲率为
是一向上凸的连续曲线,其上任意一点(x,y)的曲率为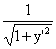 ,又此曲线上点(0,1)处的切线方程为y=x+1,求该曲线的方程,并求函数y=y(x)的极值
,又此曲线上点(0,1)处的切线方程为y=x+1,求该曲线的方程,并求函数y=y(x)的极值
11.
12.(1)(1996,III)求微分方程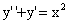 的通解
的通解
(2)(2000,III)求微分方程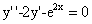 满足条件
满足条件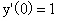 ,
,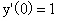 的特解
的特解
13.(1)(1990,I)求微分方程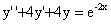 的通解
的通解
(2)(1996,I,II)求微分方程 的通解
的通解
(3)(1996,III)求微分方程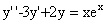 的通解
的通解
(4)(1994,III)求微分方程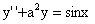 的通解,其中常数a>0
的通解,其中常数a>0
14.(1994,IV)设函数满足条件
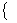
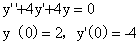
求广义积分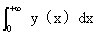
15.(2005,II)用变量代换 化简微分方程
化简微分方程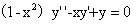 ,并求其满足
,并求其满足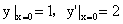 的特解
的特解
16.(1995,I,II)设曲线L位于第一象限内,L上任一点M处的切线与y轴相交,交点记为A.已知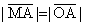 ,且过点
,且过点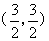 ,求L的方程
,求L的方程
17.(2003,IV)设y=f(x)是第一象限内连接点A(0,1),B(1,0)的一段连续曲线,M(x,y)为该曲线上任意一点,点C为M在x轴上的投影,O为坐标原点.若梯形OCMA的面积与曲边三角形CBM的面积之和为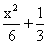 ,求f(x)的表达式
,求f(x)的表达式
18.(1995,III)设单位质点在水平面内作直线运动,初速度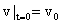 .已知阻力与速度成正比(比例系数为1),问t为多少时质点的速度为
.已知阻力与速度成正比(比例系数为1),问t为多少时质点的速度为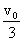 ?并求此时刻该质点所经过的路程
?并求此时刻该质点所经过的路程
19.(1997,I)在某一个人群中推广新技术是通过其中已掌握新技术的人进行的,设该人群的总人数为N,在t=0时刻已掌握新技术的人数为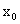 ,在任意时刻t已掌握新技术的人数为x(t)(将x(t)视为可微变量),其变化律与已掌握新技术人数和未掌握新技术人数之积成正比,比例系数k>0,求x(t)
,在任意时刻t已掌握新技术的人数为x(t)(将x(t)视为可微变量),其变化律与已掌握新技术人数和未掌握新技术人数之积成正比,比例系数k>0,求x(t)
20.(1997,II)设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内大于零,并且满足方程 (a为常数),又曲线y=f(x)与x=1,y=0所围的图形S的面积为2,求函数y=f(x),并问a为何值时,图形S绕x轴旋转一周所得的旋转体的体积最小
(a为常数),又曲线y=f(x)与x=1,y=0所围的图形S的面积为2,求函数y=f(x),并问a为何值时,图形S绕x轴旋转一周所得的旋转体的体积最小
21.(1997,II)设曲线L的极坐标方程为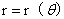 ,
,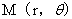 为L上任一点,
为L上任一点,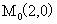 为L上一定点,若极径
为L上一定点,若极径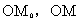 与曲线所围成的曲边扇形面积等于L上
与曲线所围成的曲边扇形面积等于L上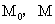 两点间弧长值的一半,求曲线L的方程
两点间弧长值的一半,求曲线L的方程
22.(1993,IV)假设
(1)函数 满足条件
满足条件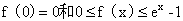
(2)平行于y轴的动直线MN与曲线y=f(x)和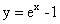 分别交于
分别交于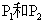
(3)曲线y=f(x),直线MN与x轴所围封闭图形的面积S恒等于线段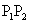 的长度,求函数y=f(x)的表达式
的长度,求函数y=f(x)的表达式
23.(2002,II)求微分方程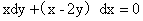 的一个解y=y(x),使得由曲线y=y(x)与直线x=1,x=2以及x轴所围成的平面图形绕x轴的旋转体体积最小
的一个解y=y(x),使得由曲线y=y(x)与直线x=1,x=2以及x轴所围成的平面图形绕x轴的旋转体体积最小
24.(2001,II)设L是一条平面曲线,其上任意一点P(x,y)(x>0)到坐标原点的距离恒等于该点处的切线在y轴上的截距,且L经过点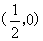
(1)试求曲线L的方程;
(2)求位于第一象限部分的一条切线,使该切线与L以及两坐标所围图形的面积最小
25.(2003,II)设位于第一象限的曲线y=f(x)过点 ,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分
,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分
(1)求曲线y=f(x)的方程
(2)已知曲线 上的弧长为
上的弧长为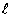 ,试用
,试用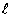 表示曲线的弧长s
表示曲线的弧长s
26.(2007,IV)设函数f(x)具有连续的一阶导数,且满足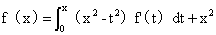 ,求f(x)的表达式
,求f(x)的表达式
27.(2012,I,II,III)已知f(x)满足方程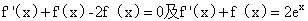
(1)求f(x)的表达式
(2)求曲线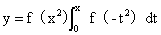 的拐点
的拐点
补充习题答案
1.(1)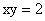 (2)
(2) (3)
(3)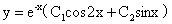 (4)
(4) (5)
(5)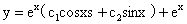 (6)
(6) (7)
(7) (8)
(8)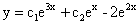 (9)
(9)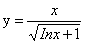 (10)
(10) (11)
(11) (12)
(12) (13)
(13)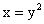
2.(1)A (2)C (3)
27.
