§1.2 常微分方程基本概念习题及解答
1. =2xy,并满足初始条件:x=0,y=1的特解。
=2xy,并满足初始条件:x=0,y=1的特解。
解: =2xdx 两边积分有:ln|y|=x
=2xdx 两边积分有:ln|y|=x +c
+c
y=e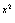 +e
+e =cex
=cex
 另外y=0也是原方程的解,c=0时,y=0
另外y=0也是原方程的解,c=0时,y=0
原方程的通解为y= cex ,x=0 y=1时 c=1
,x=0 y=1时 c=1
特解为y= e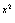 .
.
2. y dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。
dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。
解:y dx=-(x+1)dy
dx=-(x+1)dy 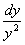 dy=-
dy=-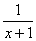 dx
dx
两边积分: - =-ln|x+1|+ln|c| y=
=-ln|x+1|+ln|c| y=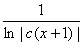
另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e
特解:y=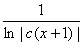
3. =
=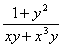
解:原方程为: =
=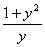

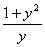 dy=
dy= dx
dx
两边积分:x(1+x )(1+y
)(1+y )=cx
)=cx
4. (1+x)ydx+(1-y)xdy=0
解:原方程为: 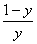 dy=-
dy=-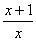 dx
dx
两边积分:ln|xy|+x-y=c
另外 x=0,y=0也是原方程的解。
5.(y+x)dy+(x-y)dx=0
解:原方程为:
 =-
=-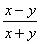
令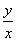 =u 则
=u 则 =u+x
=u+x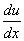 代入有:
代入有:
-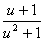 du=
du= dx
dx
ln(u +1)x
+1)x =c-2arctgu
=c-2arctgu
即 ln(y +x
+x )=c-2arctg
)=c-2arctg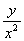 .
.
6. x -y+
-y+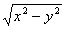 =0
=0
解:原方程为:  =
=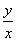 +
+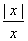 -
-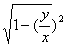
则令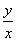 =u
=u  =u+ x
=u+ x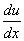
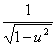 du=sgnx
du=sgnx  dx
dx
arcsin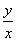 =sgnx ln|x|+c
=sgnx ln|x|+c
7. tgydx-ctgxdy=0
解:原方程为: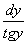 =
=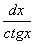
两边积分:ln|siny|=-ln|cosx|-ln|c|
siny=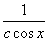 =
=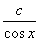 另外y=0也是原方程的解,而c=0时,y=0.
另外y=0也是原方程的解,而c=0时,y=0.
所以原方程的通解为sinycosx=c.
8  +
+ =0
=0
解:原方程为: =
= e
e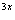
2 e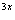 -3e
-3e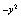 =c.
=c.
9.x(lnx-lny)dy-ydx=0
解:原方程为: =
=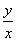 ln
ln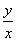
令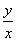 =u ,则
=u ,则 =u+ x
=u+ x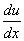
u+ x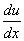 =ulnu
=ulnu
ln(lnu-1)=-ln|cx|
1+ln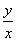 =cy.
=cy.
10.  =e
=e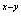
解:原方程为: =e
=e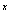 e
e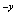
e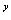 =ce
=ce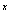
11  =(x+y)
=(x+y)
解:令x+y=u,则 =
=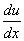 -1
-1
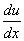 -1=u
-1=u
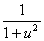 du=dx
du=dx
arctgu=x+c
arctg(x+y)=x+c
12.  =
=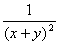
解:令x+y=u,则 =
=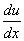 -1
-1
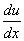 -1=
-1=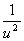
u-arctgu=x+c
y-arctg(x+y)=c.
13.  =
=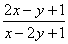
解: 原方程为:(x-2y+1)dy=(2x-y+1)dx
xdy+ydx-(2y-1)dy-(2x+1)dx=0
dxy-d(y -y)-dx
-y)-dx +x=c
+x=c
xy-y +y-x
+y-x -x=c
-x=c
14:  =
=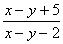
解:原方程为:(x-y-2)dy=(x-y+5)dx
xdy+ydx-(y+2)dy-(x+5)dx=0
dxy-d(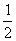 y
y +2y)-d(
+2y)-d(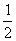 x
x +5x)=0
+5x)=0
y +4y+x
+4y+x +10x-2xy=c.
+10x-2xy=c.
15:  =(x+1)
=(x+1)  +(4y+1)
+(4y+1)  +8xy
+8xy
解:原方程为: =(x+4y)
=(x+4y) +3
+3
令x+4y=u 则 =
=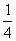
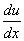 -
-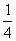
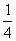
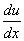 -
-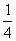 =u
=u +3
+3
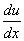 =4 u
=4 u +13
+13
u=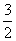 tg(6x+c)-1
tg(6x+c)-1
tg(6x+c)=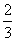 (x+4y+1).
(x+4y+1).
16:证明方程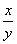
 =f(xy),经变换xy=u可化为变量分离方程,并由此求下列方程:
=f(xy),经变换xy=u可化为变量分离方程,并由此求下列方程:
1)y(1+x y
y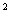 )dx=xdy
)dx=xdy
2)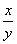
 =
=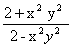
证明: 令xy=u,则x +y=
+y=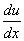
则 =
=
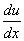 -
-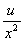 ,有:
,有:
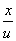
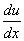 =f(u)+1
=f(u)+1
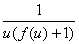 du=
du= dx
dx
所以原方程可化为变量分离方程。
1)令xy=u 则 =
=
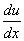 -
-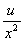 (1)
(1)
原方程可化为: =
=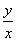 [1+(xy)
[1+(xy) ] (2)
] (2)
将1代入2式有:
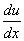 -
-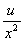 =
= (1+u
(1+u )
)
u=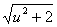 +cx
+cx
17.求一曲线,使它的切线坐标轴间的部分初切点分成相等的部分。
解:设(x +y )为所求曲线上任意一点,则切线方程为:y=y’(x- x )+ y
则与x轴,y轴交点分别为:
x= x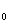 -
-  y= y
y= y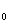 - x
- x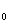 y’
y’
则 x=2 x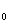 = x
= x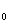 -
-  所以 xy=c
所以 xy=c
18.求曲线上任意一点切线与该点的向径夹角为0的曲线方程,其中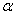 =
=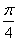 。
。
解:由题意得:y’=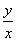
 dy=
dy= dx
dx
ln|y|=ln|xc| y=cx.
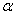 =
=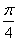 则y=tg
则y=tg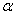 x 所以 c=1 y=x.
x 所以 c=1 y=x.
19.证明曲线上的切线的斜率与切点的横坐标成正比的曲线是抛物线。
证明:设(x,y)为所求曲线上的任意一点,则y’=kx
则:y=kx +c 即为所求。
+c 即为所求。
第二篇:高中化学必修一第一节 化学实验基本方法 教学过程讲义及习题(超具体超有用)
教 案

教 案

