常微分方程算法的应用
（杨牧原20096313）
一、常微分方程算法背景
科学研究和工程技术中许多问题在数学上往往归结为微分方程求解问题。为了确定微分方程的解，一般要加上定解条件，根据不同的情况，这些定解条件主要有初始条件和边界条件。只含初值条件作为定解条件的微分方程求解问题称为初值问题；例如在天文学中研究星体运动，空间技术中研究物体飞行等，都需要求解常微分方程初值问题。只含边界条件作为定解条件的微分方程求解问题称为边值问题。
除特殊情形外，微分方程一般求不出解析解，即使有的能求出解析解，其函数表示也比较复杂，计算量比较大，而且实际问题往往只要求在某一时刻解的函数值。为了解决这个问题，有两种方法可以逼近原方程的解。第一种方法是：将原微分方程化简为可以准确求解的微分方程，然后使用化简后的方程解近似原方程的解。第二种方法是：将求原微分方程的解析解，转化成求原微分方程的数值解，这是实际中最常用的方法。本课程设计所指常微分方程算法，即求微分方程解初值问题解的数值方法。
对于微分方程解初值问题解的数值方法，常用的有欧拉方法、改进的欧拉法、龙格库塔方法、单步法、线性多步法等。
二、数值解的一般概念
常微分方程初值问题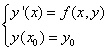
的数值解是指通过一定的近似方法得出准确解
在一列离散点
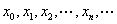上的近似值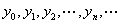
。数值解的特征是步进式，即
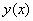在
点的近似值
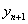是由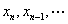
等若干点处的近似值
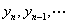的信息给出的递推公式。若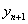依赖于前面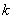
步的值
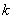，则称为步法；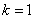
称为单步法。
利用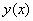在
的精确解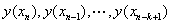
借助某种算法计算出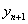，则称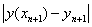
为该方法的局部截断误差。如果一个算法的局部截断误差是
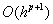，则称该方法是
阶的；而利用数值解得到的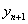与微分方程的精确解之差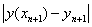称为整体截断误差，即是该数值方法的误差。
对于固定的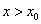
，取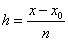
，用某种算法得到
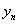，如有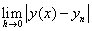
=0，则称该方法是收敛的。注意，因
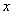是固定的，随着
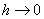，数值解的步数
。
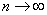在实际计算时由于舍入误差不可避免，实际得到数值解是
，稳定性即研究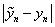
是否随着计算步骤
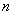的增加而增加。通常所提的稳定性是通过模型方程
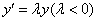来讨论的。若当某一步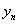有舍入误差时，在以后的计算中误差不会逐步扩大，则称这种稳定性为绝对稳定性。
三、常用的数值方法
（1）Euler法：
Euler法
的局部截断误差为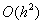
，整体截断误差为
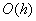，即一阶收敛。对于模型问题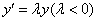，当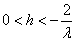
时，Euler法是数值稳定的。
隐式Euler法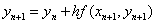
的误差与Euler法相同，但是无条件稳定：即对任意步长
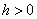，隐式Euler法都是稳定的。
梯形法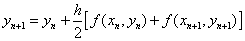
的误差比Euler法高一阶，也是无条件稳定的。
改进Euler法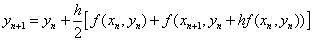
是一种预测－校正方法：
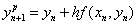——Euler法预测
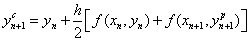——梯形法校正
它保持了梯形法的误差阶数，但不是无条件稳定的。
（2）龙格-库塔方法
龙格-库塔类算法采用区间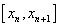
内若干点的斜率的加权平均来近似整个区间的平均斜率，一般形式为
如经典的4级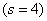
4阶（局部截断误差为
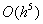）Runge-Kutta公式为
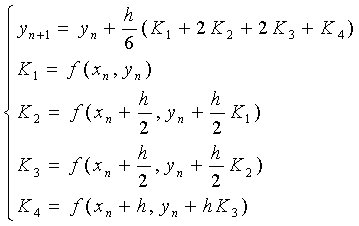
（3）线性多步法
线性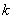步法具有一般形式
（2）
为隐式公式；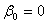
为显式公式。构造多步法公式有基于数值积分和Taylor展开两种途径。多步法（2）的局部截断误差为
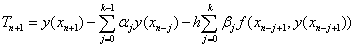
利用原微分方程后，成为
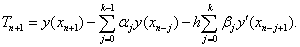
因此利用Taylor公式，分别对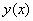和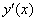
作Taylor展开，可确定线性多步（2）中的待定参数
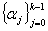和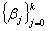
，使它达到最高阶精度（或指定精度）。
预测－校正格式：不论单步法还是多步法，隐式公式比显式公式的稳定性好，但隐式公式的计算比较困难。预测－校正格式是用显式公式进行预测，再用隐式公式进行校正。
四、常微分方程算法的MATLAB实现
本课程设计采用两个常微分方程实例，用MATLAB实现其数值解法。即用欧拉公式和四阶龙格-库塔法分别求解下列初值问题；
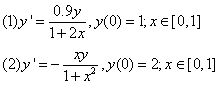
运行结果：
取步长h=0.1，计算（1）、（2）
用欧拉公式计算的（1）、（2）从y0到y10分别为：
y1 =
1.000000000000000
1.075000000000000
1.144107142857143
1.208463169642857
1.268886328125000
1.325986212890625
1.380231103417969
1.431989769796143
1.481558646442932
1.529180174364312
1.575055579595242
y2 =
2.000000000000000
2.198019801980198
2.620715917745621
3.342013876758177
4.494432454950652
6.292205436930913
9.068178423812199
13.328396475267596
19.830053292471302
29.690300785965320
44.535451178947980
用四阶龙格-库塔法公式计算的（1）、（2）从y0到y10分别为：
y3 =
1.000000000000000
1.071830686020710
1.138210603070936
1.200165937159814
1.258439052626425
1.313587198654128
1.366041104260767
1.416141729504544
1.464164360144417
1.510334991353230
1.554841814242189
y4 =
2.000000000000000
2.029485726123789
2.077698895268894
2.143376082752966
2.224971284406619
2.320806154955647
2.429195959276118
2.548539314792825
2.677371870326064
2.814390789711760
2.958458858618671
五、结论
算法分析：取步长为h=0.1，分别用欧拉及四阶龙格-库塔方法进行计算。欧拉初值公式为：y.n+1=y.n+h*f(t.n-1,y.n),y.0=a;四阶龙格-库塔公式为:k1=f(tn,yn), k2=f(tn+h/2,yn+h*k1/2),k3=f(tn+h/2,yn+h*k2/2),k4=f(tn+h,yn+h*k3), y.n+1=y.n+(h/6)*(k1+2*k2+2*k3+k4).
从上面的运行结果可知，四阶龙格库塔方法具有高得多的精确度。但需要指出的是，龙格库塔方法是基于泰勒展开法，因而求方程的解具有足够的光滑性。如果解的光滑性差，使用四阶龙格库塔方法求得数值解的精确度，可能不如改进的欧拉方法精确度高。因此，在实际的计算中，要根据具体问题的特性，选择合适的算法。
六、参考文献
[1] 朱晓临主编《数值分析》 中国科学技术大学出版社， 2010
[2] 关治，陆金甫编著《数值分析基础》 高等教育出版社，2008
附录：源程序
disp('取步长h=0.1，计算（1）、（2）')
y1=zeros(11,1);y2=zeros(11,1);
y1(1)=1; y2(1)=2; k=1;
for i=1:10
y1(k+1)=y1(k)+0.1*(0.9*y1(k)/(1+2*k*0.1));
y2(k+1)=y2(k)+(k*0.1)*y2(k)/(1+(k*0.1)*(k*0.1));
k=k+1;
end
disp('用欧拉公式计算的（1）、（2）从y0到y10分别为：')
y1
y2
y3=zeros(11,1);y4=zeros(11,1);
y3(1)=1; y4(1)=2;
k=1; h=0.1;
for i=1:10
k1=0.9*y3(k)/(1+2*h*k);
k2=0.9*(y3(k)+h*k1/2)/(1+2*(h*k+h/2));
k3=0.9*(y3(k)+h*k2/2)/(1+2*(h*k+h/2));
k4=0.9*(y3(k)+h*k3)/(1+2*(h*k+h));
y3(k+1)=y3(k)+h*(k1+2*k2+2*k3+k4)/6;
m1=(k*h)*y4(k)/(1+(k*h*k*h));
m2=(h*k+h/2)*(y4(k)+h*m1/2)/(1+(h*k+h/2)*(h*k+h/2));
m3=(h*k+h/2)*(y4(k)+h*m2/2)/(1+(h*k+h/2)*(h*k+h/2));
m4=(h*k+h)*(y4(k)+h*m3)/(1+(h*k+h)*(h*k+h));
y4(k+1)=y4(k)+h*(m1+2*m2+2*m3+m4)/6;
k=k+1;
end
disp('用四阶龙格-库塔法公式计算的（1）、（2）从y0到y10分别为：')
y3
y4
第二篇：非线性常微分方程边值问题的最优化算法
第27卷第4期
20xx年08月工程数学学报CHINESEJOURNALOFENGINEERINGMATHEMATICSVol.27No.4Aug.2010文章编号:1005-3085(2010)04-0663-06
非线性常微分方程边值问题的最优化算法?
侯祥林,钱颖,吴海涛
(沈阳建筑大学理学院，沈阳110168)
摘要:本文提出了一种新的优化方法以精确地解决微分方程的边值问题。针对非线性微分方程边值问题
打靶法的不足，以未知的部分初始条件为设计变量，以给定的边界函数值与设计变量之间的关系，形成复杂嵌套式程式化的目标函数，建立了求解未知初始条件的优化问题，并采用VisualBasic6.0语言编制了求解未知初始条件的程序，给出了典型算例，并通过比较，验证了本文求解方法的正确性。
中图分类号:O175.8;O224文献标识码:A关键词:非线性微分方程；边值问题；优化方法；程序设计分类号:AMS(2000)34B15
1引言
非线性常微分方程边值问题是工程中常见的理论和实际问题[1-5]，通常采用有限差分法和打靶法分析求解。目前应用最多的求解方法是打靶法[6]。无论单级和多级打靶求解方法，通过下面步骤求解：1)选取待求的初值；2)采用微分方程初值问题算法按步迭代计算，获得终点边界值；3)应用计算边界值与给定真实边界值的误差函数，重新调整待求的初值，直到使得误差函数达到一定精度为止。总的看这种计算过程比较繁琐。最优化方法是能良好解决工程实际问题的数学方法[7]。笔者曾提出动态设计变量优化方法通过巧妙进行动态设计变量处理，构造目标函数，已经解决了许多工程实际问题[8-10]。本文针对非线性微分方程边值问题，提出一种以待求初值为设计变量，以误差函数构造目标函数的直接最优化算法。并通过编制最优化算法通用程序实现非线性常微分方程边值问题的精确求解。
2微分方程边值问题的最优化算法原理与程序设计
2.1微分方程边值问题
设任意一个n阶非线性常微分方程
?????y(n)=fx,y,y,y,···,y(n?1),(1)
边界条件
y(k)(a)=y(k),k=i1,i2,···,in1,y(l)(b)=y(l),l=j1,j2,···,jm,···,jn2,(2)
其中i1,i2,···,in1和j1,j2,···,jm,···,jn2为小于n的互异正整数，且n1+n2=n。
收稿日期:2009-03-11.作者简介:侯祥林(19xx年5月生)，男，博士后，教授.研究方向：非线性系统分析与控制.?基金项目:辽宁省自然科学基金(20072011)；国家“十一五”科技支撑计划重点项目(2008BAJ09B02-2)；辽宁省教育厅项目(L2010445).
664
工程数学学报第27卷
?
??
求解方程(1)边界问题的实质是寻找一种可行的方法，确定其中一个边界点的所有y,y,y,···,y(n?1)的值，使得问题成为初值问题。对于x=a点，已知y(k)(a)=y(k),k=i1,i2,···,in1，n1个值，而y(l)(a),l=j1,j2,···,jm,···,jn2，n2个值是未知的。边值问题算法将确定y(l)(a),l=j1,j2,···,jm,···,jn2，这n2个未知量。下面将给出求法与算例。2.2算法原理
?
首先，设y1=y,y2=y,···,yn=y(n?1)，将(1)转化为状态方程
??y˙1=y2,??????y˙=y3,???2
(3)···,
?????y˙n?1=yn,?????y˙n=f(x,y1,y2,···,yn?1),边界条件转化为
yk(a)=yk,
构建最优化问题
minf(z),
n2
???2
yjm(z,b)?yjm(b),f(z)=
m=1
k=i1,i2,···,in1,yl(b)=yl,l=j1,j2,···,jn2.
(4)(5)
设计变量z=[z1,z2,···,zn2]T，表示待求的初始值yl(a),l=j1,j2,···,jn2。yjm(z,b),m=
1,2,···,n2，为含有待求设计变量的复杂嵌套显式的函数。其计算借助于数值积分Runge-Kutta[11]算法，由程式按步迭代计算获得的边界x=b处相应各阶函数值。这样，该问题转化为寻求待求设计变量，使目标函数获得极小值问题。其理想解条件为f(z)→0，即yl(z,b)=yl(b),l=j1,j2,···,jn2。因此其优化求解过程相当于求解非线性方程组yjm(z,b)=yjm(b),m=1,2,···,n2的解。2.3目标函数的形成程序
目标函数程式化的形成步骤为：给定自变量x，计算步长为h。给x∈[a,b]分段。h=(b?a)/M,xk=a+kh,k=0,1,2,···,M,x0=a,xM=b。
1)由已知初始条件yk(a)=yk(x0)=yk,k=1,2,···,in1和待求初始条件yjm(x0)=zm,m=1,2,···,in2；采用R-K方法进行一步计算，获得yk(x1),k=1,2,···,n，它们是关于z的函数；
2)由yk(x1),k=1,2,···,n，计算yk(x2),k=1,2,···,n，它们是关于z的函数；3)由yk(xi),k=1,2,···,n，计算yk(xi+1),k=1,2,···,n，它们是关于z的函数；4)由yk(xM?1),k=1,2,···,n，计算yk(xM),k=1,2,···,n；5)最后可以形成目标函数
f(z)=
2.4
坐标轮换方法概述
n2??i=1
?2
yjm(z,b)?yjm(b).
第4期侯祥林等：非线性常微分方程边值问题的最优化算法
665
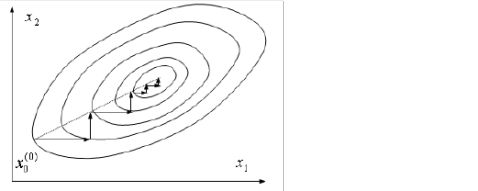
下面给出以二维问题为例的多维坐标轮换法优化过程计算原理，参见图1，在x1Ox2平
(0)(0)(0)面上，任取初始点x(0)=[x1,x2]T，从x(0)出发，先沿x1轴方向搜索，x2=x2固定
(0)(1)不变，仅改变x1使目标函数值下降，由minf(x1,x2)一维搜索获得相应的最优点x1=
(1)(0)(1)(1)(1)[x1,x2]T；然后再以x1为起点，x1=x1固定不变，仅改变x2，沿x2轴方向，由minf(x1,
(1)(1)(1)x2)一维搜索获得相应的最优点x2=[x1,x2]T；完成一轮搜索，进行收敛条件判定，
当满足精度时，停止迭代，否则从x12出发进行下轮搜索计算，直到满足精度获得最优
??T点x?1=[x1,x2]为止。对于n维问题有同样的计算过程。
图1:梯度法搜索过程示意图
2.5程序组成
论文采用VisualBasic编制计算程序[12]，程序模块组成含有：1)主程序；2)一维搜索子程序段；3)坐标轮换法子段；4)动态设计变量目标函数子段。
2.6解的存在性与精度问题
1)解的存在性问题：本文的优化方法与差分法和打靶法相比，仍属数值算法范畴，是基于微分方程边界问题的解存在为假设前提条件下的一种更为精确算法。本文不讨论微分方程边界问题解不存在的情况。
2)步长对精度的影响：本文微分方程迭代计算过程，均采用四阶显式Runge-Kutta法，它的稳定区域为(?2.78,0)，通常步长越小越稳定。在足够小步长条件下，计算误差随步骤增加而不断减小，具有稳定与相容性。将保证优化计算中获得的解具有收敛性。3算例分析
算例1线性常微分方程边值问题y+y=0,y(0)=0,y(π/2)=1。??
???本题为非线性常微分方程一个特例。设y1=y,y2=y，则方程转化为y1=y2,y2=
??y1。该题设计变量维数n=1，待求变量z1=y(0)=y2(0)，取步长h=π/2/10000，初
值z1(0)=0.5。设定黄金分割法精度为e=10?5，通过程序优化计算z1=0.99997。此时目标
?函数精度达到e=10?10。本题的真实解y(x)=sinx。准确值为y(0)=cos0=1.00000，优化
结果表明具有较高的计算精度。表1列出选取不同迭代步长h时，应用程序优化计算的设计变量结果和误差情况。可见迭代步长越小，将会导致优化计算结果的准确程度越高。
666
表1:
hπ/2/10000π/2/1000
工程数学学报第27卷
算例1中不同步长对于优化结果的影响
误差百分比0.0030.035
hπ/2/100π/2/10
?
优化计算的z1
?
优化计算的z1
误差百分比0.3423.365
0.999970.99965
0.996580.96635
算例2含一个未知量的非线性常微分方程边值问题
y?(1+x2)y=1,
?
?
??
y(0)=1,
?
y(1)=3.
设y1=y,y2=y，则方程转化为y1=y2,y2=1+(1+x2)y1。
?
本题设计变量维数为n=1，此时z1=y(0)=y2(0)。取步长为h=0.0001，设目标函数
?
精度为e=10?5，初值z1(0)=0.5，程序优化计算得z1=0.6419，即y(0)=0.6419。以此初值，应用R-K方法计算，列出x间隔为0.01-0.05的精确解，见表2。图2为优化计算后初值所确定的函数和导数随坐标变化过程。
表2:
x0.000.010.020.030.040.050.060.070.080.09
y11.00651.01321.02021.02731.03461.04211.04991.05781.066
y
?
算例2中应用优化后初值所计算的函数值y1.0743···1.11921.16951.22531.28691.35451.42841.50891.5965
y
?
x0.10···0.150.200.250.300.350.400.450.50
x0.550.600.650.700.750.800.850.900.910.92
y1.69161.79471.90642.02742.15842.30042.45442.62142.65652.6921
y
?
x0.930.940.950.960.970.980.991.00
y2.72842.76532.80282.84092.87972.91912.95923.0000
y
?
0.64190.66190.6820.70220.72240.74280.76320.78370.80430.825
0.8458···0.95151.06041.17331.29091.41391.54321.67991.8250
1.97992.14592.32452.51772.72732.95573.20553.47953.53753.5967
3.6573.71843.78113.84513.91033.97694.04484.1141
543210
y’
y
00.20.40.60.81
x
图2:优化计算后初值所确定的函数和导数随坐标的变化过程
第4期侯祥林等：非线性常微分方程边值问题的最优化算法
??
667
算例3Du?ng方程y+y+0.5y3=0。
?
首先以初始条件y(0)=1,y(0)=2，按步长为h=0.0001，以R-K算法直接计算出x=
???
1时，y(1)=1.4524,y(1)=?1.4243。形成含二个未知量的非线性常微分方程边值问题y+
??
y+0.5y3=0，边值条件y(1)=1.4524,y(1)=?1.4243，用优化算法反求y(0)和y(0)。本
?
00
题设计变量为n=2。设y(0)=z1,y(0)=z2，步长仍取为h=0.0001，任取z1=0.5,z2=0.5，黄金分割法精度为e=10?5，多维目标函数精度为e=10?10。应用优化程序分析，经
??
过17轮×2=34次优化计算，目标函数达到设定精度。得z1=0.9999,z2=1.9990，结果对真实初值具有非常高的逼近精度，表明方法有效。将优化过程中设计变量和目标函数的变化过程列在表3。
表3:
优化次数
0246810121416
z10.51.21161.09441.04751.02541.01381.00771.00421.0023
z20.51.60281.81331.9031.94741.97051.98351.99031.9942
opf2.01346566200.09632313340.01747092760.00427580580.00119965560.00035261040.00011107890.00003378050.0000101650
算例3优化求解过程
优化次数182022242628303234
z11.00121.00061.00031.00011.00001.00001.00000.99990.9999
z21.99631.99751.99821.99861.99871.99881.99891.99891.9990
opf0.00000308990.00000090470.00000033820.00000006650.00000002590.00000000900.00000000320.00000000110.0000000001
4结论
本文基于优化原理，提出了非线性常微分方程边值问题的直接优化算法。编制边值问题的通用的求解程序。真实地分析求解了待求未知量为1个和2个的线性和非线性常微分方程边值问题的算例。精确的计算结果，表明论文所提出算法求解这类问题的可行性。为进一步理论研究与工程应用提供良好条件。
参考文献：
[1]蔡遂林.常微分方程[M].杭州：浙江大学出版社，2008
CaiSL.OrdinaryDi?erentialEquation[M].Hangzhou:ZhejiangUniversityPress,2008[2]葛渭高.非线性常微分方程边值问题[M].北京：科学出版社，2007
GeWG.BoundaryValueProblemsinNonlinearOrdinaryDi?erentialEquations[M].Beijing:SciencePress,2007
[3]王文霞.一类二阶非线性积分一微分方程的边值问题[J].工程数学学报，2005,22(3):555-558
WangWX.Boundaryvalueproblemsforsecond-ordernonlinearintegro-di?erentialequations[J].ChineseJournalofEngineeringMathematics,2005,22(3):555-558
[4]GuptaCP.Solvabilityofathree-pointnonlinearboundaryvalueproblemforasecondorderordinary
di?erentialequation[J].MathAnalAppl,1992,168:540-551
668工程数学学报第27卷
[5]GuptaCP,Tro?mchukSI.Solvabilityofmulti-pointboundaryvalueproblemandrelatedaprioriesti-
mates[J].CanadApplMathQuart,1998,6(1):45-60
[6]凌复华等.常微分方程数值方法及其在力学中的应用[M].重庆：重庆大学出版社，1990
LingFH,etal.NumericalMethodsforOrdinaryDi?erentialEquations&itsApplicationinDynamics[M].Chongqing:ChongqingUniversityPress,1990
[7]郭科，陈聆，魏友华.最优化方法及其应用[M].北京：高等教育出版社，2007
GuoK,ChenL,WeiYH.OptimizationMethodanditsApplication[M].Beijing:HigherEducationPress,2007
[8]侯祥林，戴丽.旋转倒立双摆摆起控制量的动态设计变量优化[J].应用力学学报，2005,22(3):404-408
HouXL,DaiL.Dynamicdesignvariableoptimizationofswing-upcontrolaboutrotatingdouble-invertedpendulum[J].ChineseJournalofAppliedMechanics,2005,22(3):404-408
[9]侯祥林，陈长征，虞和济等.神经网络权值和阈值的优化方法[J].东北大学学报，1999,20(4):447-450
HouXL,ChenCZ,YuHJ,etal.Optimummethodaboutweightsandthresholdsofneuralnetwork[J].NortheasternUniversityJournals,1999,20(4):447-450
[10]侯祥林，李和玉，刘杰.最大值最小化问题优化算法与多自由度动力减振器参数计算[J].振动与冲击，2008,
27(1):100-103
HouXL,LiHY,LiuJ.Optimalalgorithmforminimizationofmaximumvalueproblemsandapplicationofdynamicabsorborwithmulti-dof[J].JournalofVibrationandShock,2008,27(1):100-103
[11]李庆扬，王能超，易大义.数值分析[M].武汉：华中科技大学出版社，2006
LiQY,WangNC,YiDY.NumericalAnalysis[M].Wuhan:HuazhongUniversityofScienceandTechnologyPress,2006
[12]林卓然.VB语言程序设计[M].北京：电子工业出版社，2003
LinZR.VBProgrammingLanguagep[M].Beijing:PublishingHouseofElectronicsIndustry,2003
OptimizationAlgorithmofBoundaryValueProblemforNonlinear
OrdinaryDi?erentialEquations
HOUXiang-lin,QIANYing,WUHai-tao
(SchoolofScience,ShenyangJianzhuUniversity,Shenyang110168)
Abstract:Inthispaper,anoptimizationmethodisappliedtoaccuratelysolveaboundaryvalueproblemofordinarydi?erentialequations.Inviewoftheweaknessoftheshootingmethod,thisstudytreatstheinitialconditionsoftheunknownpartsasdesignvariablesandconductscomplicatedobjectivefunctionbasedontherelationshipbetweenthegivenboundaryvaluesanddesignvariables.Andtherefore,anewoptimizationalgorithmtocomputeinitialconditionsofunknownpartsisproposed,whichis?nallyveri?edbyemployingVisualBasic6.0todesignauniverseprogram,providingtypicalexamplesandmakingcomparisonwiththeexistentresults.
Keywords:nonlinearordinarydi?erential;boundaryvalueproblem;optimizationalgorithm;programdesign
Received:11Mar2009.Accepted:22Oct2009.
Foundationitem:TheNatureScienceFoundationofLiaoningProvince(20072011);theNational‘eleven-?ve’Science&TechnologyResearchProgram(2008BAJ09B02-2);theEducationDepartmentProjectofLiaoningProvince(L2010445).