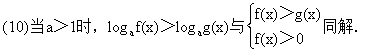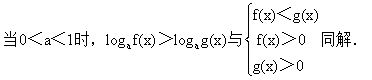1．不等式的定义：a-b>0a>b, a-b=0a=b, a-b<0a<b。?

　　① 其实质是运用实数运算来定义两个实数的大小关系。它是本章的基础，也是证明不等式与解不等式的主要依据。?

　　②可以结合函数单调性的证明这个熟悉的知识背景，来认识作差法比大小的理论基础是不等式的性质。?

　　作差后，为判断差的符号，需要分解因式，以便使用实数运算的符号法则。?

　　如证明y=x3为单增函数，?

　　设x1, x2∈(-∞,+∞), x1<x2，f(x1)-f(x2)=x13-x23=(x1-x2)(x12+x1x2+x22)=(x1-x2)[(x1+)2

+x22]?

　　再由(x1+)2+x22>0, x1-x2<0,可得f(x1)<f(x2), ∴ f(x)为单增。?

　　2．不等式的性质：?

　　① 不等式的性质可分为不等式基本性质和不等式运算性质两部分。

不等式基本性质有：?

　　(1) a>bb<a (对称性)?

　　(2) a>b, b>ca>c (传递性)?

　　(3) a>ba+c>b+c (c∈R)?

　　(4) c>0时，a>bac>bc?

　　　　c<0时，a>bac<bc。?

　　运算性质有：?

　　(1) a>b, c>da+c>b+d。?

　　(2) a>b>0, c>d>0ac>bd。?

　　(3) a>b>0an>bn?(n∈N, n>1)。?

　　(4) a>b>0>(n∈N, n>1)。?

　　应注意，上述性质中，条件与结论的逻辑关系有两种：“”和“”即推出关系和等价关系。一般地，证明不等式就是从条件出发施行一系列的推出变换。解不等式就是施行一系列的等价变换。因此，要正确理解和应用不等式性质。?

　　② 关于不等式的性质的考察，主要有以下三类问题：?

　　(1)根据给定的不等式条件，利用不等式的性质，判断不等式能否成立。?

　　(2)利用不等式的性质及实数的性质，函数性质，判断实数值的大小。?

　　(3)利用不等式的性质，判断不等式变换中条件与结论间的充分或必要关系。??

第二篇：不等式总结

不等式总结

一、不等式的性质

1．（不等式建立的基础）两个实数a与b之间的大小关系

  

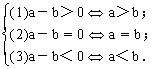
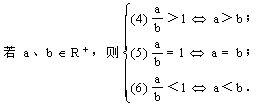
2．不等式的性质

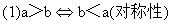
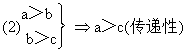
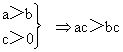
(4)                                   (乘法单调性)

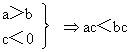
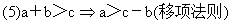
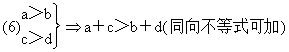   ---不等式相加

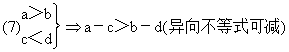    ---不等式相减

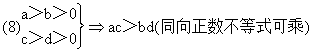---不等式相乘

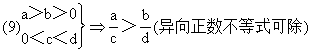  --不等式相除

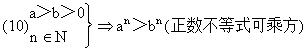     乘方法则

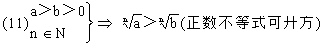  _{开方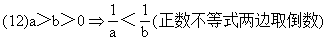   ----}倒数法则

3．绝对值不等式的性质

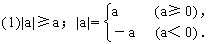
(2)如果a＞0，那么

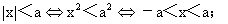
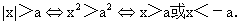
(3)|a·b|＝|a|·|b|．

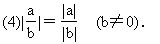
(5)|a|－|b|≤|a±b|≤|a|＋|b|．

(6)|a₁＋a₂＋……＋a_n|≤|a₁|＋|a₂|＋……＋|a_n|．

4. 基本不等式

（1）如果a，b是正数，那么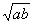≤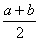，当且仅当a=b时，等号成立。

注意：基本不等式的证明是利用重要的不等式推导的，即

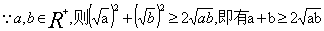
（2）基本不等式又称为均值定理、均值不等式等。其中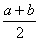称为a，b的算术平均数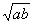，称为a，b的几何平均数。两个正数的算术平均数不小于它们的几何平均数。

（3）均值不等式中“当且仅当”的含义：

①当a=b，取等号，即a=b＝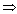

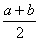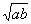
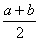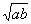
②仅当a=b时取等号，即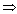＝a=b

（4）几种变形公式

ab≤(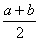)²≤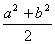(a,b∈R)  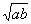  ≤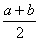≤(a＞0, b＞0)

5. 柯西不等式

（1）代数形式：

设a₁，a₂，b₁，b₂均为实数，(a₁²＋a₂²)( b₁² + b₂²)≥(a₁ b₁+ a₂ b₂) ² （注：等号成立条件：a₁ b₂= a₂ b₁）

（2）向量形式：|α||β|≥|α·β|，α=(a₁,a₂,…,a_n)，β=(b₁,b₂,…,b_n)（n∈N，n≥2）

等号成立条件：β为零向量，或α=λβ（λ∈R）。

（3）三角不等式：由|α|＋|β|≥|α+β|可得：设a₁，a₂，b₁，b₂均为实数，则

√(a₁²＋a₂²)＋√(b₁² + b₂²)≥√[(a₁+ b₁)²＋(a₂ + b₂)²] （注：等号成立条件：存在非负实数μ及λ使得μa₁=λb₁，μa₂=λb₂其中“√”表示平方根）

（4）平面三角不等式：设a₁，a₂，b₁，b₂ ，，c₂均为实数，则

√[ (a₁-b₁)²＋(a₂-b₂)²]＋√[ (b₁-c₁) ²＋(b₂-c₂)²]≥√[(a₁-c₁)²＋(a₂-c₂)²] （注：等号成立条件：存在非负实数μ及λ使得μ(a₁- b₁)=λ(b₁- c₁) , μ(a₂- b₂)=λ(b₂- c₂)其中“√”表示平方根）

(5)设α，β，γ为平面向量，则|α-β|+|β-γ|≥|α-γ|。当α-β，β-γ为非零向量时。（注：等号成立条件：存在正常数λ，使得α-β＝λ（β-γ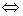）向量α-β与β-γ同向，即夹角为零。

（6）一般形式：设a₁，a₂，…，a_n，b₁，b₂ …，b_n均为实数，则

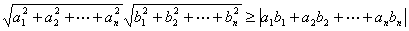
注：等号成立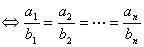

6. 排序不等式：

（1）定义：设有两组数 a₁ , a₂ ,…… a_n; b₁ , b₂ ,…… b_n 满足 a₁ ≤ a₂ ≤……≤ a_n, b₁ ≤ b₂ ≤……≤ b_n ，其中c₁,c₂,……,c_n是b₁,b₂,……，b_n的任一排列，则称a₁ b₁ + a₂ b₂+ ... + a_n b_n 为这两个实数组的顺序积之和（简称顺序和），称a₁ b_n + a₂b_{n-1}+ ... + a_n b₁  为这两个实数组的反序积之和（简称反序和），称a₁ c₁ + a₂ c₂ +…+ a_n c_n  为这两个实数组的乱序积之和（简称乱序和）

（2）定理：（排序不等式，又称排序原理）设有两组数 a₁ , a₂ ,… a_n; b₁ , b₂ ,… b_n 满足 a₁ ≤ a₂ ≤…≤ a_n, b₁ ≤ b₂ ≤…≤ b_n ，其中c₁,c₂,…,c_n是b₁,b₂,…，b_n的任一排列，那么

a₁ b_n + a₂b_{n-1}+ ... + a_n b₁ ≤ a₁ c₁ + a₂ c₂ +……+ a_n c_n ≤ a₁ b₁ + a₂ b₂ + ……+a_n b_n.

当且仅当 a₁ = a₂ = ... = a_n 或 b₁ = b₂ = ... = b_n 时等号成立，即反序和等于顺序和。

排序原理可简记作：反序和≤乱序和≤顺序和。

7. 贝努利不等式：

定理：设x＞-1，且x≠0，n为大于1的自然数，则(1+x)ⁿ≥1+nx.

二、不等式的证明

1．不等式证明的依据

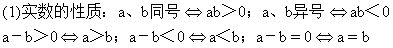
(2)不等式的性质(略)

(3)重要不等式：

①|a|≥0；a²≥0；(a－b)²≥0(a、b∈R)（非负数）

②a²＋b²≥2ab(a、b∈R，当且仅当a=b时取“=”号)

④ a³+b³+c³≥3abc(a,b,c∈R⁺)

⑤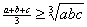

⑥ |a|－|b|≤|a±b|≤|a|＋|b|．

⑦ |a₁＋a₂＋……＋a_n|≤|a₁|＋|a₂|＋……＋|a_n|．

⑧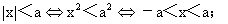

⑨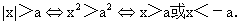

2．不等式的证明方法

(1) 比较法：要证明a＞b(a＜b)，只要证明a－b＞0(a－b＜0)，这种证明不等式的方法叫做比较法．

用比较法证明不等式的步骤是：作差——变形——判断符号．

(2) 综合法：从已知条件出发，依据不等式的性质和已证明过的不等式，推导出所要证明的不等式成立，这种证明不等式的方法叫做综合法．

(3) 分析法：从欲证的不等式出发，逐步分析使这不等式成立的充分条件，直到所需条件已判断为正确时，从而断定原不等式成立，这种证明不等式的方法叫做分析法．

（4）三角换元法：多用于条件不等式的证明，如果所给条件较复杂，一个变量不易用另一个变量表示，这时可考虑用三角代换，将两个变量都用同一个参数表示，此法如果运用恰当，可沟通三角与代数的联系，将复杂的代数问题转化为三角问题。

注意：根据具体问题，常用的三角换元技巧有：

① x²+y²=1,可设x=cosα,y=sinα；

② a≤ x²+y²≤b，可设x=rcosα,y=rsinα, a≤r²≤b

③ 对于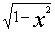，由于|x|≤1,可设x=cosα（0≤α≤π）或x=sinα(-π/2≤α≤π/2)

④ 对于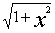,可设x=tanα(-π/2＜α＜π/2)或x=cotα(0＜α＜π)

⑤ 对于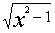,可设x=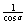 (0≤α＜π/2或π/2＜α≤π)或x= 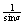(-π/2≤α＜0或0＜α≤π/2)

⑥ 对于x+y+z=xyz,由于在ΔABC中有tanA+tanB+tanC=tanAtanBtanC,可设x=tanA,y=tanB,z=tanC(A+B+C=π)。

（5）放缩法：要证明不等式A＜B，有时可以将它的一边放大或缩小，寻找一个中间量，如将A放大成C，即A＜C，后证C＜B，这种证法叫放缩法。常用技巧有：舍掉（或加进）一些项，在分式中放大或缩小分子或分母；应用基本不等式放缩。

    放缩法的理论依据主要有：不等式的传递性、等量加不等量为不等量、同分子（分母）异分母（分子）的两个分式大小的比较。

证明不等式除以上三种基本方法外，还有反证法、数学归纳法、综合分析法、放缩法、函数法、几何法、其它方法（换元法、判别式法、导数法、构造法）、柯西不等式等。

（5）利用基本不等式比较实数大小或证明不等式

① 利用均值定理求最值，必须满足三个条件：：“一正”各项均为正数 、“二定”和或积为常数、“三相等”等号必须成立。和定积最大，积定和最小。

② 构造定值条件的常用技巧：加项变换、拆项变换、统一换元、平方后利用不等式。

③ 基本不等式：

若x，y是正数，有x+y=S（和为定值），则当x=y时，积xy=取最大值；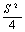

若x，y是正数，有xy=P（积为定值），则当x=y时，和x+y=取最小值；2。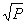

三、解不等式

1．解不等式问题的分类

(1)解一元一次不等式．

(2)解一元二次不等式．

(3)可以化为一元一次或一元二次不等式的不等式．

①解一元高次不等式；

②解分式不等式；

③解无理不等式；

④解指数不等式；

⑤解对数不等式；

⑥解带绝对值的不等式；

⑦解不等式组．

2．解不等式时应特别注意下列几点：

(1) 正确应用不等式的基本性质．

(2) 正确应用幂函数、指数函数和对数函数的增、减性．

(3) 注意代数式中未知数的取值范围．

3．不等式的同解性

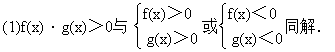
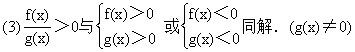
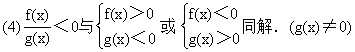
(5)|f(x)|＜g(x)与－g(x)＜f(x)＜g(x)同解．(g(x)＞0)

(6)|f(x)|＞g(x)①与f(x)＞g(x)或f(x)＜－g(x)(其中g(x)≥0)同解；②与g(x)＜0同解．

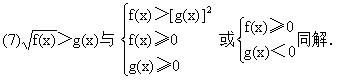
(9)当a＞1时，a^f(x)＞a^g(x)与f(x)＞g(x)同解，当0＜a＜1时，a^f(x)＞a^g(x)与f(x)＜g(x)同解．