不等式
一、知识点:
1. 实数的性质:
a?b?a?b?0
;a?b?a?b?0;a?b?a?b?0.
2. 不等式的性质:

3. 常用基本不等式:

4.利用重要不等式求最值的两个命题:
命题1:已知a,b都是正数,若ab是实值P,则当a=b=命题2:已知a,b都是正数,若a+b是实值S,则当a=b=
时,和a+b有最小值2s2
. .
时,积ab有最大值
s
2
4
注意:运用重要不等式求值时,要注意三个条件:一“正”二“定”三“等”,即各项均为正数,和或积为定值,取最值时等号能成立,以上三个条件缺一不可.
5.一元二次不等式的解法:设a>0,x1x2是方程ax2+bx+c=0的两个实根,且x1≤x2,则有
结论:ax2+bx+c>0?
6. 绝对值不等式 a?0?或a?0检验?2?b?4ac?0;ax2+bx+c<0???2a?0?b?4ac?0或a?0检验
(1)|x|<a(a>0)的解集为:{x|-a<x<a};
|x|>a(a>0)的解集为:{x|x>a或x<-a}。
(2)||a|?|b||?|a?b|?|a|?|b|
7. 不等式证明方法:
基本方法:比较法、综合法、分析法、反证法
辅助方法:换元法(三角换元、均值换元等)、放缩法、构造法、判别式法
特别提醒:不等式的证明,方法灵活多样,它可以和很多内容结合.高考解答题中,常渗透不等式证明的内容,最常用的思路是用分析法探求证明途径,再用综合法加以叙述。我们在利用不等式的性质或基本不等式时要注意等号、不等号成立的条件。
例:解下列不等式:
(1) x?7x?12?0; (2) ?x?2x?3?0;
(3) x?2x?1?0; (4) x?2x?2?0.
解:(1)方程x?7x?12?0的解为x1?3,x2?4.根据y?x?7x?12的图象,可得原不等式x?7x?12?0的解集是{x|x?3或x?4}.
22222222(2)不等式两边同乘以?1,原不等式可化为x?2x?3?0.
方程x?2x?3?0的解为x1??3,x2?1.
根据y?x?2x?3的图象,可得原不等式?x?2x?3?0的解集是{x|?3?x?1}.

222
(3)方程x?2x?1?0有两个相同的解x1?x2?1.
根据y?x?2x?1的图象,可得原不等式x?2x?1?0的解集为?.
(4)因为??0,所以方程x?2x?2?0无实数解,根据y?x?2x?2的图象,可得原不等式x?2x?2?0的解集为?.
练习1. (1)解不等式
(2)解不等式222222x?3x?3(若改为?0呢?) ?0;x?7x?7?1; 2x?3
x?7
?x?7?0,?x?7?0,解:(1)原不等式??或??{x|?7?x?3} x?3?0x?3?0??
(该题后的答案:{x|?7?x?3}).
(2)x?10
x?7?0即?{x|?7?x?10}.
8、最值定理
设x、y都为正数,则有
⑴ 若x?y?s(和为定值),则当x?y时,积xy取得最大值s
42.
⑵ 若xy?p(积为定值),则当x?y时,和x?
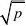
y取得最小值.
即:“积定,和有最小值;和定,积有最大值”
注意:一正、二定、三相等
几种常见解不等式的解法 重难点归纳
解不等式对学生的运算化简等价转化能力有较高的要求,随着高考命题原则向能力立意的进一步转化,
(1)熟练掌握一元一次不等式(组)、一元二次不等式(组)
(2)掌握用零点分段法解高次不等式和分式不等式,特别要注意因式的处理方法
(3)掌握无理不等式的三种类型的等价形式,指数和对数不等式的几种基本类型的解法
(4)
(5)
(6)对于含字母的不等式,要能按照正确的分类标准,进行分类讨论
典型题例示范讲解
例1:如果多项式f(x)可分解为n个一次式的积,则一元高次不等式f(x)?0(或f(x)?0)可用“穿根法”求解,但要注意处理好有重根的情况. 当分式不等式化为f(x)
g(x)?0(或?0)时,要注意它的等价变形
①f(x)
g(x)
f(x)?0?f(x)?g(x)?0 ②?f(x)?g(x)?0f(x)?0??或
?0?f(x)?0或f(x)?g(x)?0 g(x)?0g(x)g(x)?
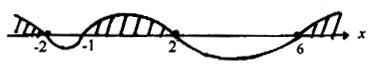
用“穿根法”解不等式时应注意:①各一次项中x的系数必为正;②对于偶次或奇次重根可转化为不含重根的不等式,也可直接用“穿根法”,但注意“奇穿偶不穿”,其法如下图.

不等式左右两边都是含有x的代数式,必须先把它们移到一边,使另一边为0再解. 例:解不等式:(1)2x3?x2?15x?0;(2)(x?4)(x?5)2(2?x)3?0. 解:(1)原不等式可化为
x(2x?5)(x?3)?0
把方程x(2x?5)(x?3)?0的三个根x1?0,x2??
过三个根,其解集如下图的阴影部分.
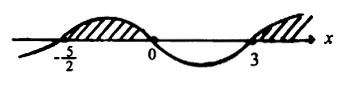
52,x3?3顺次标上数轴.然后从右上开始画线顺次经
∴原不等式解集为?x???5??x?0或x?3? 2?
(2)原不等式等价于
(x?4)(x?5)(x?2)?023
?x??5?x?5?0????(x?4)(x?2)?0??x??4或x?2
∴原不等式解集为?xx??5或?5?x??4或x?2?
解下列分式不等式:
例:(1)3
x?2?1?2
x?2; (2)x?4x?1
3x?7x?222?1
(1)解:原不等式等价于
3
x?2
??xx?2?3x?2?xx?2?0?x?5x?623(x?2)?x(x?2)
(x?2)(x?2)
(x?6)(x?1)?0?(x?2)(x?2)?0 ??(x?6)(x?1)(x?2)(x?2)?0?0??(x?2)(x?2)?(x?2)(x?2)?0
用“穿根法”
∴原不等式解集为(??,?2)???1,2???6,???。
2x?3x?1
3x?7x?222(2)解法一:原不等式等价于
22?0 ?(2x?3x?1)(3x?7x?2)?0
22???2x?3x?1?0?2x?3x?1?0??或? 22??3x?7x?2?0??3x?7x?2?0
?x?1
3或1
2?x?1或x?2
11∴原不等式解集为(??,)?(,1)?(2,??)。

32
解法二:原不等式等价于(2x?1)(x?1)
(3x?1)(x?2)?0
?(2x?1)(x?1)(3x?1)?(x?2)?0
用“穿根法” ∴原不等式解集为(??,)?(,1)?(2,??) 3211
例2:绝对值不等式,解此题的关键是去绝对值符号,而去绝对值符号有两种方法:一是根据绝对值的意义a???a(a?0)
??a(a?0) 二是根据绝对值的性质:x?a??a?x?a,xa?x?a或x??a,因此本题有如下两种解法. 例:解不等式x2?4?x?2
解:原不等式等价于 ?(x?2)?x?4?x?2 2
2???2?x?3?x?4?x?2即? ∴?故1?x?3. 2??x?1或x??2?x?4??(x?2)
例3:已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m、n∈[-1,1],m+n≠0时
>0 f(m)?f(n)m?n
(1)用定义证明f(x)在[-1,1]上是增函数;
(2)f(x+1
2)<f(1x?1);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围 技巧与方法(1)问单调性的证明,利用奇偶性灵活变通使用已知条件不等式是关键,(3)问利用单调性把
f(x)转化成“1
(1)证明任取x1<x2,且x1,x2∈[-1,1],则f(x1)-f(x2)=f(x1)+f(-x2)=f(x1)?f(?x2)
x1?x2·(x1-x2)
∵-1≤x1<x2≤1,
∴x1+(-x2)≠0,由已知f(x1)?f(?x2)
x1?x2>0,又 x1-x2<0,
∴f(x1)-f(x2)<0,即f(x)在[-1,1
(2)∵f(x)在[-1,1]上为增函数, 1??1?x??1?2?13??1 {x|-≤x<-1,x∈R} ∴??1?x?12?
11?x???2x?1?
(3)由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,
故对x∈[-1,1],恒有f(x)≤1,
所以要f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,即要t2-2at+1≥1成立,
故t-2at≥0,记g(a)=t-2at,对a∈[-1,1],g(a)≥0,
只需g(a)在[-1,1]上的最小值大于等于0,g(-1)≥0,g(1)≥0,
解得,t≤-2或t=0或t≥
∴t{t|t≤-2或t=0或t≥2} 22
例5:解关于x的不等式
解原不等式可化为a(x?1)x?2>1(a≠1) (a?1)x?(2?a)
x?2
a?2
a?1>0, ①当a>1时,原不等式与(x-
由于a?2
a?1?1?1
a?1?1?2 )(x-2)>0同解
∴原不等式的解为(-∞,a?2
a?1)∪(2,+∞
②当a<1时,原不等式与(x-
由于a?2
a?1?1?
a?21a?1?1?a?2a?1)(x-2) <0同解 , 1?2,解集为(a?2若a<0,a?1a?1
1若a=0时,?1??2,解集为?; a?1a?1a?1a?2,2);
若0<a<1,a?2
a?1?1?1
a?1?2,解集为(2,
a?2
a?1a?2a?1) a?2a?1综上所述当a>1时解集为()∪(2,+∞);当0<a<1时,解集为(2,);当a=0时,
解集为?;当a<0时,解集为(a?2
a?1,2
例6 设m?R,解关于x的不等式m2x2?2mx?3?0. 分析:进行分类讨论求解.
解:当m?0时,因?3?0一定成立,故原不等式的解集为R. 当m?0时,原不等式化为(mx?3)(mx?1)?0;
当m?0时,解得?
当m?0时,解得1
m3m?x?1m3m; .
?
?3m1??; m??x??∴当m?0时,原不等式的解集为?x??x?
当m?0时,原不等式的解集为?x
??1m?x??3??. m?
说明:解不等式时,由于m?R,因此不能完全按一元二次不等式的解法求解.因为当m?0时,原不等式化为?3?0,此时不等式的解集为R,所以解题时应分m?0与m?0两种情况来讨论.
的解是x?1.
例8 解关于x的不等式x2?(a?a2)x?a3?0.
分析:不等式中含有字母a,故需分类讨论.但解题思路与一般的一元二次不等式的解法完全一样:求出方程x2?(a?a2)x?a3?0的根,然后写出不等式的解,但由于方程的根含有字母a,故需比较两根的大小,从而引出讨论.
解:原不等式可化为(x?a)(x?a2)?0.
(1)当a?a2(即a?1或a?0)时,不等式的解集为:
?xx?a或x?a2?;
(2)当a?a2(即0?a?1)时,不等式的解集为:
?x2x?a或x?a; ?
(3)当a?a2(即a?0或1)时,不等式的解集为:
?xx?R且x?a?.
说明:对参数进行的讨论,是根据解题的需要而自然引出的,并非一开始就对参数加以分类、讨论.比如本题,为求不等式的解,需先求出方程的根x1?a,x2?a2,因此不等式的解就是x小于小根或x大于大根.但a与a两根的大小不能确定,因此需要讨论a?a,a?a,a?a三种情况. 2222
例9 不等式ax2?bx?2?0的解集为?x?1?x?2?,求a与b的值.
分析:此题为一元二次不等式逆向思维题,要使解集为?x?1?x?2?,不等式ax2?bx?2?0需满足条件a?0,??0,ax2?bx?2?0的两根为x1??1,x2?2.
解法一:设ax2?bx?2?0的两根为x1,x2,由韦达定理得:
b??bx?x?????1?212????aa 由题意:? ?22?x?x??????1?212??a??a
∴a?1,b??1,此时满足a?0,??b2?4a?(?2)?0.
解法二:构造解集为?x?1?x?2?的一元二次不等式:
(x?1)(x?2)?0,即x?x?2?0,此不等式与原不等式ax?bx?2?0应为同解不等式,故需满足: a
1?b
?1??2
?222 ∴a?1,b??1.
例10 解关于x的不等式ax2?(a?1)x?1?0.
分析:本题考查一元一次不等式与一元二次不等式的解法,因为含有字母系数,所以还考查分类思想. 解:分以下情况讨论
(1)当a?0时,原不等式变为:?x?1?0,∴x?1
(2)当a?0时,原不等式变为:(ax?1)(x?1)?0 ①
①当a?0时,①式变为(x?1
a)(x?1)?0,∴不等式的解为x?1或x?1
a.
②当a?0时,①式变为(x?
∵
1
a1a?1?1?aa1a)(x?1)?0. ② 1a?1,此时②的解为1?x?,∴当0?a?1时,1a.当a?1时,1a?1,此时②的解为?x?1.
说明:解本题要注意分类讨论思想的运用,关键是要找到分类的标准,就本题来说有三级分类:
?a?0
??a?0???a?R??0?a?1 ?
?a?0?a?0?a?1????a?1?????
分类应做到使所给参数a的集合的并集为全集,交集为空集,要做到不重不漏.另外,解本题还要注意在讨论a?0时,解一元二次不等式ax2?(a?1)x?1?0应首选做到将二次项系数变为正数再求解.
例11解不等式x2?3x?10?8?x.
分析:无理不等式转化为有理不等式,要注意平方的条件和根式有意义的条件,f(x)?g(x)可转化为f(x)?g(x)或f(x)?g(x),而f(x)?g(x)等价于:
?f(x)?0
?f(x)?0?或?g(x)?0. ?g(x)?0??2f(x)?[g(x)]?
解:原不等式等价于下面两个不等式组:
?8?x?0
?8?x?0?①?2 ②?x2?3x?10?0
?x?3x?10?0?22?x?3x?10?(8?x)
由①得??x?8
?x?5或x??2,∴x?8 ?
?x?8?74?x?8, 由②得∴?x?5或x??2 13?74?x?13.?
所以原不等式的解集为?x
??74????x?8或x?8?,即为?xx??. 1313???
f(x)?g(x)型的不等式求解,注意: 74说明:本题也可以转化为
?f(x)?0?
f(x)?g(x)??g(x)?0
?2?f(x)?[g(x)]
例12.已知关于x的不等式x2?mx?n?0的解集是{x|?5?x?1},求实数m,n之值. 解:?不等式x2?mx?n?0的解集是{x|?5?x?1}
?x1??5,x2?1是x?mx?n?0的两个实数根, ?m??4??5?1?m
. ?由韦达定理知:???
n??5?5?1?n??
2
练习.已知不等式ax2?bx?c?0的解集为{x|2?x?3}求不等式cx2?bx?a?0的解集. b?
2?3???a
?b??5a?
c??
解:由题意 ?2?3?, 即?c?6a.
a??a?0
??a?0
??
代入不等式cx2?bx?a?0得: 6ax2?5ax?a?0(a?0). 即6x2?5x?1?0,?所求不等式的解集为{x|?
13?x??
12.
1).恒成立问题
若不等式f?x??A在区间D上恒成立,则等价于在区间D上f?x?min?A 若不等式f?x??B在区间D上恒成立,则等价于在区间D上f?x?max?B 如(1)设实数x,y满足x2?(y?1)2?1,当x?y?c?0时,c的取值范围是______
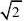
1,???)(答:; (2)不等式x?4
?x?3?a
对一切实数x恒成立,求实数a的取值范围_____
(答:a?1);
(3)若不等式2x?1?m(x2?1)对满足m?2的所有m都成立,则x的取值范围_____
(答:(
(4)若不等式(?1)na?2?值范围是_____
(答:[?2,));
23
7?12
,
3?12
));
(?1)n
n?1
对于任意正整数n恒成立,则实数a的取
(5)若不等式x2?2mx?2m?1?0对0?x?1的所有实数x都成立,求m的
取值范围.
(答:m??1
2)
2). 能成立问题
若在区间D上存在实数x使不等式f?x??A成立,则等价于在区间D上f?x?max?A;
若在区间D上存在实数x使不等式f?x??B成立,则等价于在区间D上的f?x?min?B.如 x?4?x?3?a已知不等式在实数集R上的解集不是空集,求实数a的取值
范围____
3). 恰成立问题
若不等式f?x??A在区间D上恰成立,
D;
若不等式f?x??B在区间D上恰成立,
D.
(答:a?1) 则等价于不等式f?x??A的解集为则等价于不等式f?x??B的解集为
