均值不等式应用
1. (1)若 ,则
,则 (2)若
(2)若 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
2. (1)若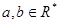 ,则
,则 (2)若
(2)若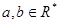 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
(3)若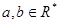 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
3.若 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
若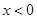 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
若 ,则
,则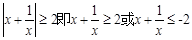 (当且仅当
(当且仅当 时取“=”)
时取“=”)
4.若 ,则
,则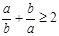 (当且仅当
(当且仅当 时取“=”)
时取“=”)
若 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
5.若 ,则
,则 (当且仅当
(当且仅当 时取“=”)
时取“=”)
『ps.(1)当两个正数的积为定植时,可以求它们的和的最小值,当两个正数的和为定植时,可以求它们的积的最小值,正所谓“积定和最小,和定积最大”.
(2)求最值的条件“一正,二定,三取等”
(3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用』
应用一:求最值
例1:求下列函数的值域
(1)y=3x 2+ (2)y=x+
解:(1)y=3x 2+≥2= ∴值域为[,+∞)
(2)当x>0时,y=x+≥2=2;
当x<0时, y=x+= -(- x-)≤-2=-2
∴值域为(-∞,-2]∪[2,+∞)
解题技巧
技巧一:凑项
例 已知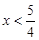 ,求函数
,求函数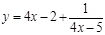 的最大值。
的最大值。
解:因 ,所以首先要“调整”符号,又
,所以首先要“调整”符号,又 不是常数,所以对
不是常数,所以对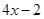 要进行拆、凑项,
要进行拆、凑项,
 ,
,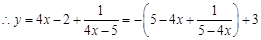

当且仅当 ,即
,即 时,上式等号成立,故当
时,上式等号成立,故当 时,
时, 。
。
评注:本题需要调整项的符号,又要配凑项的系数,使其积为定值。
技巧二:凑系数
例1. 当 时,求
时,求 的最大值。
的最大值。
解析:由 知,
知,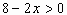 ,利用均值不等式求最值,必须和为定值或积为定值,此题为两个式子积的形式,但其和不是定值。注意到
,利用均值不等式求最值,必须和为定值或积为定值,此题为两个式子积的形式,但其和不是定值。注意到 为定值,故只需将
为定值,故只需将 凑上一个系数即可。
凑上一个系数即可。
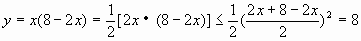
当 ,即x=2时取等号 当x=2时,
,即x=2时取等号 当x=2时, 的最大值为8。
的最大值为8。
评注:本题无法直接运用均值不等式求解,但凑系数后可得到和为定值,从而可利用均值不等式求最大值。
变式:设 ,求函数
,求函数 的最大值。
的最大值。
解:∵ ∴
∴ ∴
∴
当且仅当 即
即 时等号成立。
时等号成立。
技巧三: 分离
例3. 求 的值域。
的值域。
解析一:本题看似无法运用均值不等式,不妨将分子配方凑出含有(x+1)的项,再将其分离。

当 ,即
,即 时,
时, (当且仅当x=1时取“=”号)。
(当且仅当x=1时取“=”号)。
技巧四:换元
解析二:本题看似无法运用均值不等式,可先换元,令t=x+1,化简原式在分离求最值。
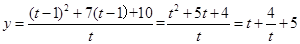
当 ,即t=
,即t= 时,
时, (当t=2即x=1时取“=”号)。
(当t=2即x=1时取“=”号)。
评注:分式函数求最值,通常直接将分子配凑后将式子分开或将分母换元后将式子分开再利用不等式求最值。即化为 ,g(x)恒正或恒负的形式,然后运用均值不等式来求最值。
,g(x)恒正或恒负的形式,然后运用均值不等式来求最值。
技巧五:在应用最值定理求最值时,若遇等号取不到的情况,结合函数 的单调性。
的单调性。
例:求函数 的值域。
的值域。
解:令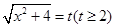 ,则
,则

因 ,但
,但 解得
解得 不在区间
不在区间 ,故等号不成立,考虑单调性。
,故等号不成立,考虑单调性。
因为 在区间
在区间 单调递增,所以在其子区间
单调递增,所以在其子区间 为单调递增函数,故
为单调递增函数,故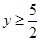 。
。
所以,所求函数的值域为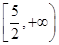 。
。
练习.求下列函数的最小值,并求取得最小值时,x 的值.
(1) (2)
(2)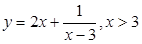 (3)
(3)
2.已知 ,求函数
,求函数 的最大值.;3.
的最大值.;3. ,求函数
,求函数 的最大值.
的最大值.
条件求最值
1.若实数满足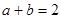 ,则
,则 的最小值是 .
的最小值是 .
分析:“和”到“积”是一个缩小的过程,而且 定值,因此考虑利用均值定理求最小值,
定值,因此考虑利用均值定理求最小值,
解: 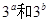 都是正数,
都是正数, ≥
≥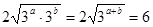
当 时等号成立,由
时等号成立,由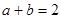 及
及 得
得 即当
即当 时,
时, 的最小值是6.
的最小值是6.
变式:若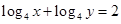 ,求
,求 的最小值.并求x,y的值
的最小值.并求x,y的值
技巧六:整体代换
多次连用最值定理求最值时,要注意取等号的条件的一致性,否则就会出错。。
2:已知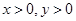 ,且
,且 ,求
,求 的最小值。
的最小值。
错解:
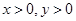 ,且
,且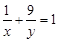 ,
,
 故
故 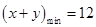 。
。
错因:解法中两次连用均值不等式,在 等号成立条件是
等号成立条件是 ,在
,在 等号成立条件是
等号成立条件是 即
即 ,取等号的条件的不一致,产生错误。因此,在利用均值不等式处理问题时,列出等号成立条件是解题的必要步骤,而且是检验转换是否有误的一种方法。
,取等号的条件的不一致,产生错误。因此,在利用均值不等式处理问题时,列出等号成立条件是解题的必要步骤,而且是检验转换是否有误的一种方法。
正解: ,
,
当且仅当 时,上式等号成立,又
时,上式等号成立,又 ,可得
,可得 时,
时, 。
。
变式: (1)若 且
且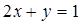 ,求
,求 的最小值
的最小值
(2)已知 且
且 ,求
,求 的最小值
的最小值
技巧七
已知x,y为正实数,且x 2+=1,求x的最大值.
分析:因条件和结论分别是二次和一次,故采用公式ab≤。
同时还应化简中y2前面的系数为 , x=x =x·
下面将x,分别看成两个因式:
x·≤== 即x=·x ≤
技巧八:
已知a,b为正实数,2b+ab+a=30,求函数y=的最小值.
分析:这是一个二元函数的最值问题,通常有两个途径,一是通过消元,转化为一元函数问题,再用单调性或基本不等式求解,对本题来说,这种途径是可行的;二是直接用基本不等式,对本题来说,因已知条件中既有和的形式,又有积的形式,不能一步到位求出最值,考虑用基本不等式放缩后,再通过解不等式的途径进行。
法一:a=, ab=·b=
由a>0得,0<b<15
令t=b+1,1<t<16,ab==-2(t+)+34∵t+≥2=8
∴ ab≤18 ∴ y≥ 当且仅当t=4,即b=3,a=6时,等号成立。
法二:由已知得:30-ab=a+2b∵ a+2b≥2 ∴ 30-ab≥2
令u= 则u2+2u-30≤0, -5≤u≤3
∴≤3,ab≤18,∴y≥
点评:①本题考查不等式
 的应用、不等式的解法及运算能力;②如何由已知不等式
的应用、不等式的解法及运算能力;②如何由已知不等式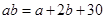
 出发求得
出发求得 的范围,关键是寻找到
的范围,关键是寻找到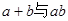 之间的关系,由此想到不等式
之间的关系,由此想到不等式
 ,这样将已知条件转换为含
,这样将已知条件转换为含 的不等式,进而解得
的不等式,进而解得 的范围.
的范围.
变式:1.已知a>0,b>0,ab-(a+b)=1,求a+b的最小值。
2.若直角三角形周长为1,求它的面积最大值。
技巧九、取平方
5、已知x,y为正实数,3x+2y=10,求函数W=+的最值.
解法一:若利用算术平均与平方平均之间的不等关系,≤,本题很简单
+ ≤==2
解法二:条件与结论均为和的形式,设法直接用基本不等式,应通过平方化函数式为积的形式,再向“和为定值”条件靠拢。
W>0,W2=3x+2y+2·=10+2·≤10+()2·()2 =10+(3x+2y)=20
∴ W≤=2
变式: 求函数 的最大值。
的最大值。
解析:注意到 与
与 的和为定值。
的和为定值。

又 ,所以
,所以
当且仅当 =
= ,即
,即 时取等号。 故
时取等号。 故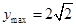 。
。
评注:本题将解析式两边平方构造出“和为定值”,为利用均值不等式创造了条件。
总之,我们利用均值不等式求最值时,一定要注意“一正二定三相等”,同时还要注意一些变形技巧,积极创造条件利用均值不等式。
应用二:利用均值不等式证明不等式
1.已知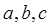 为两两不相等的实数,求证:
为两两不相等的实数,求证:
1)正数a,b,c满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc
例6:已知a、b、c ,且
,且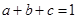 。求证:
。求证:
分析:不等式右边数字8,使我们联想到左边因式分别使用均值不等式可得三个“2”连乘,又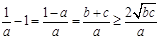 ,可由此变形入手。
,可由此变形入手。
解: a、b、c
a、b、c ,
,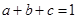 。
。
 。同理
。同理 ,
, 。上述三个不等式两边均为正,分别相乘,得
。上述三个不等式两边均为正,分别相乘,得
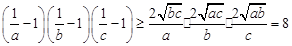 。当且仅当
。当且仅当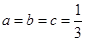 时取等号。
时取等号。
应用三:均值不等式与恒成立问题
例:已知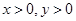 且
且 ,求使不等式
,求使不等式 恒成立的实数
恒成立的实数 的取值范围。
的取值范围。
解:令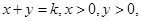
 ,
,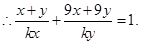

 。
。 ,
,
应用四:均值定理在比较大小中的应用:
例:若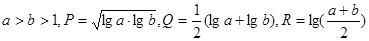 ,则
,则 的大小关系是 .
的大小关系是 .
分析:∵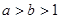 ∴
∴
 (
(
 ∴R>Q>P。
∴R>Q>P。
第二篇:不等式的实际应用
不等式的实际应用
主备人:刘玲 领导签字_____________
【学习目标】:掌握不等式解决的常见题型和方法
做差法 均值不等式法 二次函数法 【学习重点】 利用不等式解决实际问题
【学习难点】 把握题意,建立合理的不等式模型。
【课前准备及检测】
阅读教材,完成下面的问题。
1 比较aa?m,的大小,其中b>a>0,m>0. bb?m
2 某工厂第一年产量为A。第二年增长率为a,第三年的增长率为b。这两年的平均增长率为x,则( )
A x?a?ba?ba?ba?b B x? C x? D x? 2222
3 某金店用一不准确的天平(两臂不等长)称黄金,某顾客要购买10克黄金,售货员先将5克的砝码放在左盘,将黄金放在右盘,使之平衡后给顾客,然后又将5克的砝码放入右盘,将另一黄金放于左盘,使之平衡后又给顾客,则顾客时间所得黄金( )
A 大于10克 B 小于10克 C 等于10克 D 小于等于10 克
【合作探究】
题型一 用二次不等式解决实际问题
例1 有纯药液一桶,倒出8升后用水补满,然后又倒出4升后再用水补满,此时桶中的农药不超过容积的28%,问桶的容积最大为多少升?
题型二 用均值不等式解决实际问题。
例2 某公路段在某时间段内的车流量y(千辆/小时)之间有函数关系:
y?920v(v?0)。 2v?3v?1600
(1)在这段时间内,当汽车的平均速度v为多少时流量y最大?最大值是多少?
(2)为保证在该时间段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
【反思与总结】
解决实际应用题的一般步骤
【达标检测】
1 某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限一人,每天只限1次,某班有48名同学,老师打算组织同学们集体去游泳,除需购买游泳卡外,每次还要包1辆车,包车费均为40元,若使每位同学游泳8次,每人至少交多少钱?
【选做部分】
2 某出版社出版一种书,固定成本是5000元,每本书的变动成本是0.50元,售价为10.50元,该出版社销售科付出的总劳务费与销量的平方成正比,比例系数是
到不亏损,最低发行量应是多少?
1,出版社要做625
