二面角的求法
郧西四中 潘远兵
求二面角的大小是立体几何的一个重要内容,是高考的一个重点和热点,本文就二面角的求法谈谈自己的看法,希望同学们合理选择,熟练掌握,以提高解题速度。
一、 几何法:即作出二面角的平面角,再求解,此法解题过程为:作——证——算——答
根据辅助线的做法又可分为定义法、垂面法、三垂线法。
⑴定义法
在棱上找一点O在两个平面内分别作棱的垂线AOBO, ?AOB为??CD??的平面角,此法较多适用于两面是共底的等腰三角形或全等三角形。
例1 ABCD解:取BC的中点E,连接AE,DE,
∵正四面体ABCD,∴BC?AE,BC?ED于E,
∴?AED为二面角A?BC?D的平面角,
设正四面体的棱长为1,

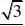
则AE?ADBEC1DE?AD?1,由余弦定理得cos?AED? 3∴?AED=arccos1. 3
(2)垂面法
过二面角内一点作棱的垂面,则这个垂面与二面角的两个面的交线的夹角就是二面角的平面角。
例2.自二面角内的一点到两个平面的距离都是6cm,两个垂足间的距离也是6cm,求此二面角的度数。
如图,P是二面角??L??内的一点,PA??,PB?,A,B分别为垂足,PA=PB=AB=6cm,L为二面角的棱,所以?APB=60,因为PA
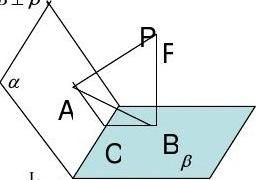
??,且PA,PB相交于P点,过PA和PB作平面分别交?,? 两个平面于AC和CB,则平面PACB?L, 所以?ACB是二面角的平面角。又PA?AC,PB?CB, 所以?PAC=?PBC=90 所以由APB=60,得?ACB=120, 即所求二面角的度数为120 (3)三垂线法
利用三垂线定理或逆定理作二面角的平面角,其特征是过其中一个平面内一点作另一个平面的垂线,然后过垂足或斜足作棱的垂线 ,从而构造二面角的平面角。
例3.如图,AB?平面BCD,BD?CD,若AB?BC?2BD,求二面角B?AC?D 1
解:过D作DE?AC于E,过E作EF?AC交BC于F,连结DF,
则C垂直于平面DEF,?FED为二面角B?AC?D的平面角,
∴AC?DF,
A又AB?平面BCD,
∴AB?DF,AB?CD,
∴DF?平面ABC,
∴DF?EF,DF?BC, B又∵AB?CD,BD?CD,
∴CD?平面ABD,∴CD?AD,
设BD?a,则AB?BC?2a,
在Rt?BCD中,
S?BCD?11BC?DF?BD?
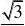
CD,∴DF?a,同理,Rt?
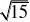
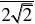
ACD中,DE?, 22DF??
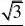
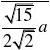

∴sin?FED?B?AC?
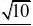
D DE二、射影面积法:通常使用于无棱的二面角的大小的计算。
即用公式cos?=S射
S原C
求解 例4. 如图ABCD是直角梯形,∠ABC=90°,SA⊥面ABCD. SA=AB=BC=1 AD=1 2求面SCD与面SBA所成的二面角的大小
-解:由于DA?平面SAB,CB?平面SAB,则?SCD在平面SAB的射影是?SAB,易求,SB=3,SD=CD?
则cos??S?SAB
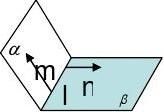
S?SCD12215,?SC上的高为,S?SCD??3?,又S?SAB?,?2224222226?=.???,即面SCD与面SBA所成的二面角的大66小为 2. 6三、向量法:(1)棱上取两点向量法 若m,n分别是二面角??l??的两个半平面内与棱l垂直的两向量,则二面角的大小就是向量m,n的夹角
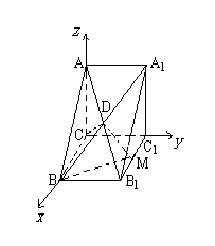
例5. 如图,直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=1,CB=2,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.
(Ⅰ)求证CD⊥平面BDM;(Ⅱ)求面B1BD与面CBD所成二面角的大小.
2
解:如图,以C为原点建立坐标系.
(Ⅰ)B(2,0,0),B1(2,1,0),A1(0,1,1),
D(2,1,1),M(2,1,0), 2222
?(21111,,),A1?(2,?1,?1),?(0,,?), 22222
则CD?A1B?0,CD?DM?0, ∴CD⊥A1B,CD⊥DM.
因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM.
(Ⅱ)设BD中点为G,连结B1G,则
??3211211231G(,CD?(,,),,),,B1G?(?,?,), 444222444
??B1?0,
???CD?B1G??又CD?BD,?cos??1???CD与B1G的夹角?等于所求的二面角的平面角.
所以所求的二面角等于??(2)法向量法 3.33. 3
设二面角??l??的两个半平面的法向量分别为m与n,即二面角?和m与n的夹角相等或互补。
例6. 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=2,AF=1,M是线段EF的中点。(Ⅰ)求证AM∥平面BDE;(Ⅱ)求二面角A—DF—B的大小; 解:(Ⅰ)建立如图所示的空间直角坐标系。设AC?BD?N,连接NE,
?2222则点N、E的坐标分别是((0,0,1), ∴NE=(?,,0)、,?,1), 2222
220)又点A、M的坐标分别是(22,、(,,1) 22
?22∴ AM=(?,?,1)∴NE=AM且NE与AM不共线,∴NE∥AM。 22
又∵NE?平面BDE, AM?平面BDE,∴AM∥平面BDF。
(Ⅱ)∵AF⊥AB,AB⊥AD,AF?AD?A,∴AB⊥平面ADF。 ∴AB?(?2,0,0)为平面DAF的法向量。
??22∵NE·DB =(?,?,1)·(?2,2,0)=0,∴NE·NF=22
?2(?,?,1)·(2,2,0)=0得:NE⊥DB,NE⊥NF,∴NE为平面BDF的法向量。∴22
??1cos<AB,NE >=AB与NE的夹角是60?。 2???
即所求二面角A—DF—B的大小是60?。
3
第二篇:二面角求法大全
二面角求法之面面观
求解二面角是立体几何中最基本、最重要的题型,也是各地高考中的“热点”问题,虽然对此可说是“千锤百炼”,但我们必须面对新的情境、新的变化,如何以基本方法的“不变”去应对题目中的“万变”就是我们研究的中心话题.
总的来说,求解二面角的大体步骤为:“作、证、求”.其中“作、证”是关键也是难点,“求”依靠的计算,也决不能忽视,否则因小失大,功亏一篑,也是十分遗憾之事.
1 定义法
即在二面角的棱上找一点,在二面角的两个面内分别作棱的射线即得二面角的平面角.定义法是“众法之源”,万变不离其宗,“树高千尺,叶落归根”,求二面角的一切方法盖源出定义这个“根”!.
例1 正方体ABCD-A1B1C1D1中,求二面角A-BD-C1的正切值为 .
分析与略解:“小题”不必“大做”,由图1知所求二面角为
二面角C-BD-C1的“补角”.教材中根本就没有“二面角的补角”
这个概念,但通过几何直观又很容易理解其意义,这就叫做直觉
思维,在立体几何中必须发展这种重要的思维能力.易知∠COC1
是二面角C-BD-C1的平面角,且tan∠COC1=2。
B C A1

C1 将题目略作变化,二面角A1-BD-C1的余弦值为 .
1
3在图1中,∠A1OC1是二面角A1-BD-C1的平面角,设出正方体的棱长,用余弦定理易求得 图1 cos∠A1OC1=
B Q P C Q P F C 1 例2(20xx年江苏试题)如图2(1),在正三角形ABC 中,E、F、P分别是AB、AC、BC上的点,满足AE: EB=CF:FA=CP:BP=1:2.如图2(2),将△AEF折起 到△A1EF的位置,使二面角A1-EF-B成直二面角,连
接A1B、A1P.
(Ⅰ)与(Ⅱ)略;(Ⅲ)求二面角B-A1P-F的余弦值。 图2(1) 图2(2)
分析与略解:在例1中,图形的对称和谐状态对解题产生了很好的启迪作用,在这里更离不开图形的这种对称和谐性.若取BP的中点Q,连接EQ,则在正三角形ABC中,很容易证得△BEQ≌△ PEQ≌△PEF≌△AEF,那么在图2(2)中,有A1Q=A1F.作FM⊥A1P于M,连接QH、QF,则易得△A1QP≌△A1FP,△QMP≌△FMP,所以∠PMQ=∠PMF=90o,∠QMF为二面角B-A1P-F的平面角,使题解取得了突破性的进展.设正三角形的边长为3,依次可求得A1P=5,QM=FM=
中,由余弦定理得cos∠QMF=?7
8255,在△QMF。
练习:2011广东高考理18.(本小题满分13分)
如图5.在锥体P-ABCD中,ABCD是边长为1的菱形,
且∠DAB=60?
,PA?PD?分别是BC,PC的中点. 1
(1) 证明:AD ?平面DEF; (2) 求二面角P-AD-B的余弦值. 解:(2) 由(1)知?PGB为二面角P?AD?B的平面角,
在Rt?PGA中
,PG2?
BG
2
BG中A,
127
t;在R??()?
24
1223
?1?()?;
24
在?
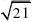
PGB中,cos?PGB?2 三垂线法
PG?BG?PB
2PG?BG
222
??
7
.
A
B
S
S
S
这是最典型也是最常用的方法,当然此法仍扎“根”于二面角平面角的定义. 此法最基本的一个模型为:如图3,设锐二面角??l??,过面?
内一点P作PA⊥?于A,作AB⊥l于B,连接PB,由三垂线定理得PB ⊥l,则∠PBA为二面角??l??的平面角,故称此法为三垂线法.
最重要的是在“变形(形状改变)”和“变位(位置变化)”中能迅速作
l
A 图3
出所求二面角的平面角,再在该角所在的三角形(最好是直角三角形,如图3中的Rt△PAB)中求解.对于钝二面角也完全可以用这种方法,锐角的补角不就是钝角吗?
例3(20xx年陕西试题)如图4,平面?⊥平面?,?∩?=l,A∈?,B∈?,点A在直线l上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=2,求:
(Ⅰ)略;(Ⅱ)二面角A1-AB-B1的正弦值.
分析与略解:所求二面角的棱为AB,不像图3的那样一看就明白 的状态,但本质却是一样的,对本质的观察能力反映的是思维的深刻性.
作A1E⊥AB1于AB1于E,则可证A1E⊥平面AB1B.过E作EF⊥A B交AB于F,连接A1F,则得A1F⊥AB,∴∠A1FE就是所求二面角的 平面角.
依次可求得AB1=B1B=,A1B=3,A1E=
22
1
A1图4
l,A1F=
32
,则在Rt△A1EF中,sin∠A1FE=
A1E. A1F3
与图3中的Rt△PAB比较,这里的Rt△A1EF就发生了“变形”和“变位”,所以要有应对各种变化,乃至更复杂变化的思想准备. 3 垂面法
事实上,图1中的平面COC1、图2(2)中的平面QMF、图3中的平面PAB、图4中的平面A1FE都是相关二面角棱的垂面,这种通过作二面角棱的垂面得平面角的方法就叫做垂面法.在某些情况下用这种方法可取得良好的效果.
例4空间的点P到二面角??l??的面?、?及棱l的距离分别
2393
P
?为4、3、,求二面角??l??的大小.
l
图5
2
分析与略解:如图5,分别作PA⊥?于A,PB⊥?于B,则易知 l⊥平面PAB,设l∩平面PAB=C,连接PC,则l⊥PC.
分别在Rt△PAC、Rt△PBC中,PC=
2393
,PA=4,PB=3,则AC=
233
,BC=
533
.
因为P、A、C、B四点共圆,且PC为直径,设PC=2R,二面角??l??的大小为?. 分别在△PAB、△ABC中,由余弦定理得
22222
AB=AC+BC-2·AC·BCcos?=PA+PB-2·PA·PBcos(???),
则可解得cos?=?4 面积法
12
,?=120o,二面角??l??的大小为120o.
1
如图1,设二面角C-BD-C1的大小为?,则在Rt△COC1中,cos??
?1C1O
2
CO
CO?BD
?
C1O?BD
S?CBDS?C1BD
,
在某些情况下用此法特别方便.
例5 如图6,平面?外的△A1B1C1在?内的射影是边长为1的正三角形ABC,且AA1=2,BB1=3,CC1=4,求△A1B1C1所在的平面与平面?所成锐二面角的余弦值
分析与略解:问题的情境很容易使人想到用面积法,分别在BB1、CC1取BD=CE=AA1, 则△A1B1C1≌△A1DE,可求得A1B=
4
1
1
2,A1C1=5,B1C1=
2,所以等腰△A1B1C1的面积为
,又正△ABC的面积为
34
.
1H M G
设所求二面角的大小为?,则cos?=5 变式二面角的求法
55
.
图6
以上列举了求解二面角的四种基本方法,但在现实中,问题往往不是那么简单与单纯,而是有诸多的变化,“源于基本方法,适应各种变化”就是我们总的策略. 5.1 “无棱”二面角的求法
严格地说,任何二面角都是有棱的,“无棱”其实是指二面角的棱处于隐含的状态.对于这样的问题,有两种处理办法:
(1)用面积法,见例5;
(2)找出隐含的棱,此法可称为“找棱法”.
在例5中,延长C1B1和C1A1分别交CB和CA的延长线于G、H,连GH. 作CM⊥GH于M,连C1M,C1M⊥GH,则∠CMC1是所求二面角的平面角. 由平几知识得CG=4,CH=2,则△CGH的面积为23,又△CGH的面积为
12
CH·CM.
3
又由余弦定理得GH=23,所以CM=2,则在Rt△CMC1中,cos?=
55
.
在原图中,面A1B1C1与?的公共点都不知道,所以必须找出它们的两个公共点,才能找到二面角的棱;而在另一些问题中,知道两个面的一个公共点,那么只须再找出另一个公共点就可以了.
面积法比找棱法似乎要简单些,但看问题不能简单化,例5的第二种解法是非常重要的一种方法,其中蕴涵的知识和技能的“营养”对于滋补人大大脑是十分有价值的,所以决不要忽视找棱法. 5.2 有关二面角的最值问题
求最值是代数、三角、解几的“热点”问题,殊不知立体几何中也有引人入胜的最值问题.
?
例6 二面角?-l-?的大小是变量?(0???),点B、C在l
2上,A、D分别在面?、?内,且AD⊥BC,AD与面?成△ABC的面积为定值S,求△BCD面积Q的最大值.
分析与略解:如图9,作AE⊥BC于E,连DE,则由AD⊥BC得
?
BC⊥平面ADE,则DE⊥BC,∠AED=?,∠ADE=.
6
?
6
角,若
图7
l在△AED中,由正弦定理得
DEAE
sin(???
sin
?6
)
?6
,所以
QS
sin(???
sin
?6
)
,Q?2Ssin(??
?6
?6
),
则当??
?
3
时,有Qmax=2S.
△BCD和△ABC有公共的底边BC,则它们的面积比等于对应高之比,这是简单的平几知识,但用在这里却发挥了以简驭繁的奇妙功能.三角函数与正弦定理给题目注入了新的活力.
4
