二面角求法之面面观
求解二面角是立体几何中最基本、最重要的题型,也是各地高考中的“热点”问题,虽然对此可说是“千锤百炼”,但我们必须面对新的情境、新的变化,如何以基本方法的“不变”去应对题目中的“万变”就是我们研究的中心话题.
总的来说,求解二面角的大体步骤为:“作、证、求”.其中“作、证”是关键也是难点,“求”依靠的计算,也决不能忽视,否则因小失大,功亏一篑,也是十分遗憾之事.
1 定义法
即在二面角的棱上找一点,在二面角的两个面内分别作棱的射线即得二面角的平面角.定义法是“众法之源”,万变不离其宗,“树高千尺,叶落归根”,求二面角的一切方法盖源出定义这个“根”!.
例1 正方体ABCD-A1B1C1D1中,求二面角A-BD-C1的正切值为 .
分析与略解:“小题”不必“大做”,由图1知所求二面角为
二面角C-BD-C1的“补角”.教材中根本就没有“二面角的补角”
这个概念,但通过几何直观又很容易理解其意义,这就叫做直觉
思维,在立体几何中必须发展这种重要的思维能力.易知∠COC1
是二面角C-BD-C1的平面角,且tan∠COC1=2。
B C A1

C1 将题目略作变化,二面角A1-BD-C1的余弦值为 .
1
3在图1中,∠A1OC1是二面角A1-BD-C1的平面角,设出正方体的棱长,用余弦定理易求得 图1 cos∠A1OC1=
B Q P C Q P F C 1 例2(20xx年江苏试题)如图2(1),在正三角形ABC 中,E、F、P分别是AB、AC、BC上的点,满足AE: EB=CF:FA=CP:BP=1:2.如图2(2),将△AEF折起 到△A1EF的位置,使二面角A1-EF-B成直二面角,连
接A1B、A1P.
(Ⅰ)与(Ⅱ)略;(Ⅲ)求二面角B-A1P-F的余弦值。 图2(1) 图2(2)
分析与略解:在例1中,图形的对称和谐状态对解题产生了很好的启迪作用,在这里更离不开图形的这种对称和谐性.若取BP的中点Q,连接EQ,则在正三角形ABC中,很容易证得△BEQ≌△ PEQ≌△PEF≌△AEF,那么在图2(2)中,有A1Q=A1F.作FM⊥A1P于M,连接QH、QF,则易得△A1QP≌△A1FP,△QMP≌△FMP,所以∠PMQ=∠PMF=90o,∠QMF为二面角B-A1P-F的平面角,使题解取得了突破性的进展.设正三角形的边长为3,依次可求得A1P=5,QM=FM=
中,由余弦定理得cos∠QMF=?7
8255,在△QMF。
练习:2011广东高考理18.(本小题满分13分)
如图5.在锥体P-ABCD中,ABCD是边长为1的菱形,
且∠DAB=60?
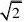
,PA?PD?分别是BC,PC的中点. 1
(1) 证明:AD ?平面DEF; (2) 求二面角P-AD-B的余弦值. 解:(2) 由(1)知?PGB为二面角P?AD?B的平面角,
在Rt?PGA中
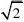
,PG2?
BG
2
BG中A,
127
t;在R??()?
24
1223
?1?()?;
24
在?
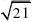
PGB中,cos?PGB?2 三垂线法
PG?BG?PB
2PG?BG
222
??
7
.
A
B
S
S
S
这是最典型也是最常用的方法,当然此法仍扎“根”于二面角平面角的定义. 此法最基本的一个模型为:如图3,设锐二面角??l??,过面?
内一点P作PA⊥?于A,作AB⊥l于B,连接PB,由三垂线定理得PB ⊥l,则∠PBA为二面角??l??的平面角,故称此法为三垂线法.
最重要的是在“变形(形状改变)”和“变位(位置变化)”中能迅速作
l
A 图3
出所求二面角的平面角,再在该角所在的三角形(最好是直角三角形,如图3中的Rt△PAB)中求解.对于钝二面角也完全可以用这种方法,锐角的补角不就是钝角吗?
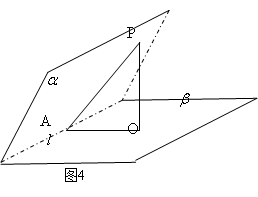
例3(20xx年陕西试题)如图4,平面?⊥平面?,?∩?=l,A∈?,B∈?,点A在直线l上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=2,求:
(Ⅰ)略;(Ⅱ)二面角A1-AB-B1的正弦值.
分析与略解:所求二面角的棱为AB,不像图3的那样一看就明白 的状态,但本质却是一样的,对本质的观察能力反映的是思维的深刻性.
作A1E⊥AB1于AB1于E,则可证A1E⊥平面AB1B.过E作EF⊥A B交AB于F,连接A1F,则得A1F⊥AB,∴∠A1FE就是所求二面角的 平面角.
依次可求得AB1=B1B=,A1B=3,A1E=
22
1
A1图4
l,A1F=
32
,则在Rt△A1EF中,sin∠A1FE=
A1E. A1F3
与图3中的Rt△PAB比较,这里的Rt△A1EF就发生了“变形”和“变位”,所以要有应对各种变化,乃至更复杂变化的思想准备. 3 垂面法
事实上,图1中的平面COC1、图2(2)中的平面QMF、图3中的平面PAB、图4中的平面A1FE都是相关二面角棱的垂面,这种通过作二面角棱的垂面得平面角的方法就叫做垂面法.在某些情况下用这种方法可取得良好的效果.
例4空间的点P到二面角??l??的面?、?及棱l的距离分别
2393
P
?为4、3、,求二面角??l??的大小.
l
图5
2
分析与略解:如图5,分别作PA⊥?于A,PB⊥?于B,则易知 l⊥平面PAB,设l∩平面PAB=C,连接PC,则l⊥PC.
分别在Rt△PAC、Rt△PBC中,PC=
2393
,PA=4,PB=3,则AC=
233
,BC=
533
.
因为P、A、C、B四点共圆,且PC为直径,设PC=2R,二面角??l??的大小为?. 分别在△PAB、△ABC中,由余弦定理得
22222
AB=AC+BC-2·AC·BCcos?=PA+PB-2·PA·PBcos(???),
则可解得cos?=?4 面积法
12
,?=120o,二面角??l??的大小为120o.
1
如图1,设二面角C-BD-C1的大小为?,则在Rt△COC1中,cos??
?1C1O
2
CO
CO?BD
?
C1O?BD
S?CBDS?C1BD
,
在某些情况下用此法特别方便.
例5 如图6,平面?外的△A1B1C1在?内的射影是边长为1的正三角形ABC,且AA1=2,BB1=3,CC1=4,求△A1B1C1所在的平面与平面?所成锐二面角的余弦值
分析与略解:问题的情境很容易使人想到用面积法,分别在BB1、CC1取BD=CE=AA1, 则△A1B1C1≌△A1DE,可求得A1B=
4
1
1
2,A1C1=5,B1C1=
2,所以等腰△A1B1C1的面积为
,又正△ABC的面积为
34
.
1H M G
设所求二面角的大小为?,则cos?=5 变式二面角的求法
55
.
图6
以上列举了求解二面角的四种基本方法,但在现实中,问题往往不是那么简单与单纯,而是有诸多的变化,“源于基本方法,适应各种变化”就是我们总的策略. 5.1 “无棱”二面角的求法
严格地说,任何二面角都是有棱的,“无棱”其实是指二面角的棱处于隐含的状态.对于这样的问题,有两种处理办法:
(1)用面积法,见例5;
(2)找出隐含的棱,此法可称为“找棱法”.
在例5中,延长C1B1和C1A1分别交CB和CA的延长线于G、H,连GH. 作CM⊥GH于M,连C1M,C1M⊥GH,则∠CMC1是所求二面角的平面角. 由平几知识得CG=4,CH=2,则△CGH的面积为23,又△CGH的面积为
12
CH·CM.
3
又由余弦定理得GH=23,所以CM=2,则在Rt△CMC1中,cos?=
55
.
在原图中,面A1B1C1与?的公共点都不知道,所以必须找出它们的两个公共点,才能找到二面角的棱;而在另一些问题中,知道两个面的一个公共点,那么只须再找出另一个公共点就可以了.
面积法比找棱法似乎要简单些,但看问题不能简单化,例5的第二种解法是非常重要的一种方法,其中蕴涵的知识和技能的“营养”对于滋补人大大脑是十分有价值的,所以决不要忽视找棱法. 5.2 有关二面角的最值问题
求最值是代数、三角、解几的“热点”问题,殊不知立体几何中也有引人入胜的最值问题.
?
例6 二面角?-l-?的大小是变量?(0???),点B、C在l
2上,A、D分别在面?、?内,且AD⊥BC,AD与面?成△ABC的面积为定值S,求△BCD面积Q的最大值.
分析与略解:如图9,作AE⊥BC于E,连DE,则由AD⊥BC得
?
BC⊥平面ADE,则DE⊥BC,∠AED=?,∠ADE=.
6
?
6
角,若
图7
l在△AED中,由正弦定理得
DEAE
sin(???
sin
?6
)
?6
,所以
QS
sin(???
sin
?6
)
,Q?2Ssin(??
?6
?6
),
则当??
?
3
时,有Qmax=2S.
△BCD和△ABC有公共的底边BC,则它们的面积比等于对应高之比,这是简单的平几知识,但用在这里却发挥了以简驭繁的奇妙功能.三角函数与正弦定理给题目注入了新的活力.
4
第二篇:二面角的求法
二面角的求法
1. 引言
二面角及其平面角的概念是立体几何最重要的概念之一,在历年高考中几乎都要涉及.尤其是在数学新课改的大环境下,要求对二面角求法的掌握变得更加灵活.二面角的概念发展、完善了空间角的概念;而二面角的平面角不但定量描述了两相交平面的相对位置,同时它也是空间中线线、线面、面面位置关系的一个汇集点.研究二面角的求法,可以进一步培养学生的空间想象能力和逻辑思维能力,为培养学生的创新意识和创新能力提供了一个良好的契机.
在求解二面角的问题中,通常首先要定位出二面角的平面角,而这也是学生在解题中感到最为陌生和棘手的问题.特别是若二面角的楞隐而不露其解题的难度又会增大.本文从二面角的概念定义入手,通过分类求解二面角的题型类别,探寻二面角的解题思路,并对二面角求解方法加以总结归类.
1.1 二面角的相关概念
 新教材
新教材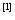 在二面角中给出的定义如下:
在二面角中给出的定义如下:
 从一条直线出发的两个半平面所组成的图形叫做二面角.
从一条直线出发的两个半平面所组成的图形叫做二面角.
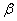 定义只给出二面角的定性描述,关于二面角的定量刻画还必须放到二面角的平面角中去研究.教材如下给出了二面角的平面角的概念:
定义只给出二面角的定性描述,关于二面角的定量刻画还必须放到二面角的平面角中去研究.教材如下给出了二面角的平面角的概念:
二面角的平面角是指在二面角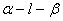 的棱上任取一点O,分别在两个半平面内作射线
的棱上任取一点O,分别在两个半平面内作射线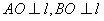 ,则
,则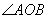 为二面角
为二面角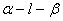 的平面角.
的平面角.
2. 二面角的求解方法
对二面角的求解通常是先定位二面角的平面角,从而将三维空间中的求角问题转化为二维空间并可以通过三角形的边角问题加以解决.定位出二面角为解题的关键环节,下面就二面角求解的步骤做初步介绍:
一、“找”:找出图形中二面角,若不能直接找到可以通过作辅助线补全图形定位二面角的平面角
二、“证”:证明所找出的二面角就是该二面角的平面角
三、“算”:计算出该平面角
由于定位二面角的难度较大,对于求解二面角还有一种思路就是绕开定位二面角这一环节,通过一些等价的结论或公式或用空间向量等方法来直接求出二面角的大小.本文将根据这两种解题思路对二面角的解题方法做一一介绍.
2.1 定位二面角的平面角,求解二面角
二面角常见题型中根据所求两面是否有公共棱可分为两类:有棱二面角、无棱二面角.对于前者的二面角的定位通常采用找点、连线或平移等手段来定位出二面角的平面角;而对于无棱二面角我们还必须通过构造图形如延展平面或找公垂面等方法使其有“无棱”而“现棱”再进一步定位二面角的平面角.
2.1.1 直接法
 对于图形中已有二面角的平面角,只要加以证明认定,然后可直接计算求解.
对于图形中已有二面角的平面角,只要加以证明认定,然后可直接计算求解.
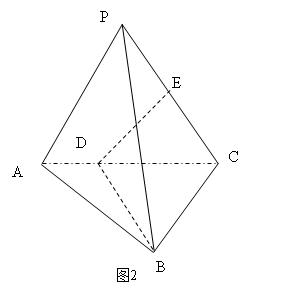
例1 如图2,已知PA^面ABC,
如图2,已知PA^面ABC,
AB^BC,PC的垂直平分线DE交AC于D,交PC于E.PA=AB=1,PB=BC求二面角E-BD-C的大小.
解: 由PE=EC,PB=BC知PC^BE,且PC^DE,可知PC^面BDE.
因BD?面BDE可得BD^PC.
由PA^面ABC,BD^面ABC知BD^PA,且BD^PC知BD^面PAC.又因DE,DC?面PAC,
故知BD^DE,BD^DC.于是可知∠CDE是二面角E-BD-C的平面角.
由PA=AB=1得PB=BC=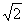 .因PA^面ABC,BC^AB,有BC^PB,可得PC=2.在RT?PAC中,∠ACP=
.因PA^面ABC,BC^AB,有BC^PB,可得PC=2.在RT?PAC中,∠ACP=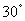 ,可得在RT?CDE中,∠CDE=
,可得在RT?CDE中,∠CDE=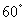 .
.
所以二面角E-BD-C的大小为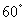
2.1.2 定义法
根据二面角平面角的定义,其解题步骤一般既是:定棱,找点,连线,解答。即:在二面角棱上选择恰当的点,过此点作出二面角的平面角,如抓住共底的等腰三角形的性质选择公共棱的中点连接得到二面角;在两个平面为共底且对应全等的三角形,可以选择公共垂足连线得到二面角的平面角等。
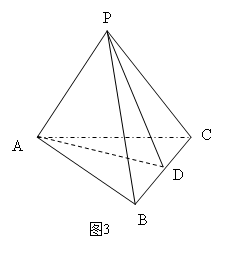 例2 在如图3所示的三棱锥P-ABC中,
例2 在如图3所示的三棱锥P-ABC中,
AB=AC=PB=PC=2,BC=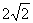 ,PA=
,PA=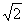 .求二面
.求二面
角P-BC-A的大小.
解:作BC中点D,连接PD,AD.因
PB=PC=AB=AC,知PD^BC,AD^BC,又有
面PBC与面ABC共棱可得∠PDA为二面角.
P-BC-A的平面角.而AB=2,BC=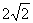 ,易知
,易知
AD=PD=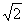 ,在RT?PAD中,
,在RT?PAD中,
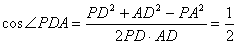
所以二面角P-BC-A的大小为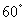 .
.
 2.1.3三垂线(逆)定理法
2.1.3三垂线(逆)定理法
根据三垂线定理及其逆定理,如图4所
示在半平面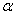 内找一点P,作PO^面
内找一点P,作PO^面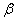 于O,并从垂足O作棱
于O,并从垂足O作棱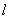 的垂线OA交棱于A点,连接PA,则∠PAO就是二面角
的垂线OA交棱于A点,连接PA,则∠PAO就是二面角 的平面角.
的平面角.
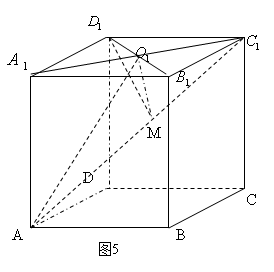
例3 在正方体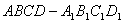 中,
中, 为面
为面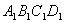 中心,求二面角
中心,求二面角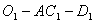 的大小.
的大小.
解:在正方体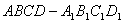 中
中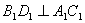 ,且
,且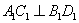 ,
,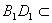
 面
面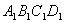 ,故
,故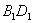
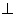
 ,
,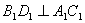
又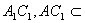 面
面 ,可知
,可知
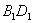
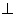

过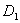 作
作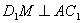 于
于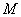 ,连接
,连接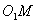 则由三垂线(逆)定理可知
则由三垂线(逆)定理可知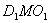 为二面角
为二面角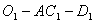 的平面角.不妨令
的平面角.不妨令 ,
,
于是,有
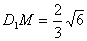 ,
,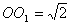 ,
,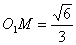 ,
,
可得
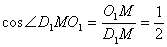
所以二面角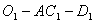 的大小为
的大小为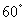
3.1.4垂面法
如果空间中有与二面角的棱垂直的平面,则该平面与两个半平面的交
线所成的角即为二面角的平面角.
上述结论可进一步引申:
推论1:空间中存在分别与二面角的两个半平面垂直的平面,则该平面与两个半平面
的交线所成的角即为二面角的平面角.
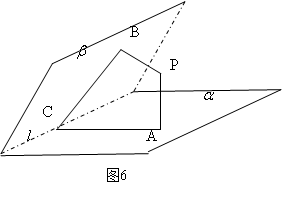 例4 如图6,二面角
例4 如图6,二面角 内一点
内一点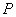 到两个半平面
到两个半平面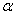 、
、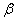 的距离分别为
的距离分别为 、
、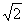 .到棱
.到棱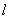 的距离为
的距离为 ,求二面角
,求二面角 的大小.
的大小.
解:作 于
于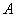 ,
,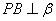 于
于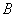 ,由
,由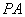 、
、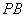 确定的平面
确定的平面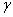 交
交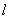 于C点,记
于C点,记 .
.
由 ,
,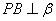 而
而 ,易知
,易知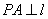
 且
且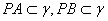 可得
可得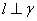 .则
.则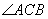 是二面角
是二面角 的平面角.
的平面角.
又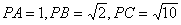 利用和角的余弦公式可求得
利用和角的余弦公式可求得
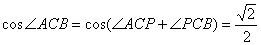
从而,知二面角 的大小为
的大小为 .
.
评注:以上四种方法是求解二面角的常用方法,也是在解决有棱二面角的通用方
法.对于方法4,下再给出解决无棱二面角的一个例子.
例5 如图7,在正三棱柱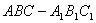 中,截面
中,截面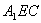 ^侧面
^侧面 ,若
,若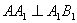 ,求平面
,求平面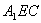 与平面
与平面 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
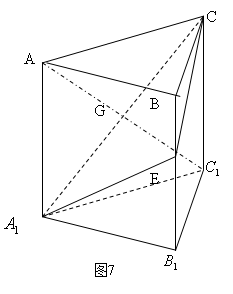 解: 设
解: 设 . 因为面
. 因为面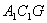 与面
与面 重合,由题意面
重合,由题意面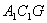 ^面
^面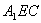 ,而
,而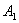 为面
为面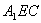 与面
与面 相交于棱上一点且
相交于棱上一点且 ,所以面
,所以面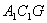 为所求二面角的一垂面,
为所求二面角的一垂面,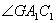 为所求二面角的平面角.
为所求二面角的平面角.
在正三棱柱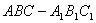 中,
中, ,可知
,可知
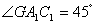
故所求二面角的大小为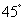 .
.
2.1.5 平移法
平移法
由空间中平行直线、平行平面的性质,利用中位线平移,平行四边形平移,
 定比分点平移等方法将所求二面角由难度较大的平面角定位转化为易知易求的平面角中进行求解.
定比分点平移等方法将所求二面角由难度较大的平面角定位转化为易知易求的平面角中进行求解.
例6(本题关键在利用平移棱
的垂线进行解题)
在正三棱柱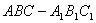
中,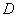 是
是 的中点,
的中点, ,求二面角
,求二面角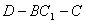 的大小.
的大小.
解:作 且交BD于F,则AE^平面
且交BD于F,则AE^平面 ,连接
,连接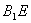 ,
, ,并记它们的交点为O连接OF,由
,并记它们的交点为O连接OF,由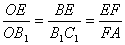 ,知
,知 .
.
由 知OF^
知OF^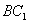 ,OE^
,OE^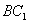 ,而
,而
 ,RT?
,RT? ?RT?
?RT? ,
,
因此
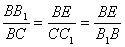
故有
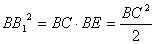
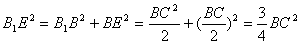
可得
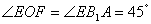
故二面角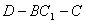 的大小为
的大小为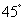 .
.
例7 在棱长为1的正方体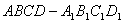 中,E是BC的中点,试求面
中,E是BC的中点,试求面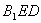 与平面
与平面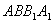 所成二面角的大小.
所成二面角的大小.
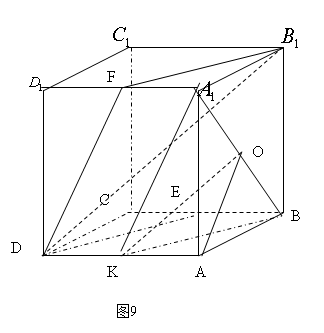 解: 取
解: 取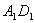 中点F,连FD,FB;
中点F,连FD,FB;
取AD中点K连接A?K,BK,A?B.显然,DE?BF为平行四边形.因为A?K//FD,KB//DE,知平面A?KB//平面DEB?F。
取A?B中点O,连接OK,OA,
由A?K=BK,A?A=BA知,
OK^A?B,OA^A?B故∠AOK为二面角的平面角.
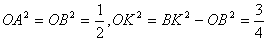
可得
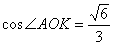
故平面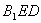 与平面
与平面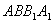 所成二面角的大小为
所成二面角的大小为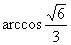 .
.
2.1.6 补体法
 通过补全一个恰当的图形或
通过补全一个恰当的图形或
延展平面使二面角更加容易定位或凸显,进而更方面求解,尤其在求解无棱二面角问题中更能现出其突出的优点.
例8 如图10,正三棱柱
如图10,正三棱柱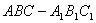 的各棱长均为1,M是棱CC?中点,求截面A?BM与底面ABC所成二面角的大小.
的各棱长均为1,M是棱CC?中点,求截面A?BM与底面ABC所成二面角的大小.
解:延长A?M与AC相交于P
点,则所求二面角即为A?-BP-A知AC=CP=BC=AB,则AB^BP, 故A?B^BP.∠ABA?是所求二面角的平面角.由AB=AA?,AA?^AB得∠ABA?=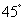
所求二面角的大小为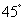 .
.
 2.1.7 无棱找棱法
2.1.7 无棱找棱法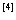
如图11中只现出两个局部半平面的一个公共点P,图中没有给出二面角的棱.此时,若在二面角的两个半平面内各存在一条直线且相互平行,则过P分别作这两条直线的垂线PQ和PR,则∠QPR就是二面角的平面角.
例9如图12,P-ABCD为正四棱锥,边长为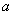 ,求平面PAB与平面PCD所成二面角的余弦值.
,求平面PAB与平面PCD所成二面角的余弦值.
解: 如图,过P点作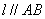 ,则
,则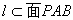 .
.
 故在P-ABCD中有
故在P-ABCD中有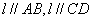 .
.
所以,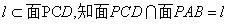 .
.
作AB中点E,CD中点F.连接PE,PF.易知PE^AB,PE^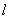 ,又PF^CD,PF^
,又PF^CD,PF^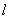 ,可知∠EPF为所求二面角的平面角.
,可知∠EPF为所求二面角的平面角.
由条件PE=PF=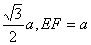 ,得到
,得到
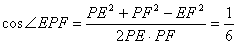
故平面PAB与平面PCD所成二面角的余弦值为 .
.
2.2不作平面角,直接求解二面角
对于有些定位二面角平面角比较困难的题目,可以绕过定位二面角的平面角这一环节,利用一些等价的公式或结论进行求解可以方面解题.
2.2.1 射影面积法
设二面角 的大小为
的大小为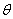 ,面
,面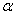 内有一个面积给S的封闭图形,给图形在面
内有一个面积给S的封闭图形,给图形在面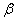 内的射影面积为
内的射影面积为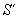 ,则
,则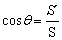 .
.
例10 求正四面体任意两个面所成二面角的大小.
解: 如图13,正四面体S-ABC,由正四面体的对称性,不妨求侧面与底面所成二面角的大小.易知
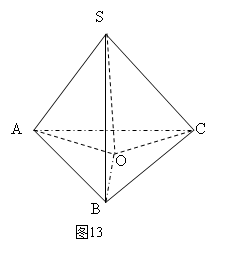
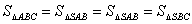
而S的射影为 的中心,所以
的中心,所以

于是有
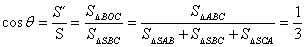
故正四面体任意两面所成二面角的大小为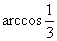 .
.
例11 如图14,在正方体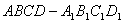 中,E为CC?中点,F在BB?上,且BF=
中,E为CC?中点,F在BB?上,且BF=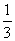 BB?,求平面A?EF在底面ABCD所成二面角的余弦值.
BB?,求平面A?EF在底面ABCD所成二面角的余弦值.
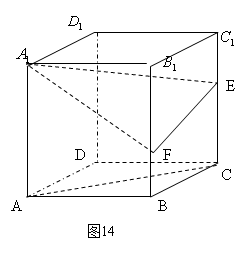 解:如图14所示,
解:如图14所示,
在正方体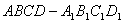 中,
中,
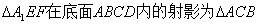 .
.
由射影面积公式知
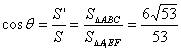
故所求二面角的余弦值为 .
.
2.2.2法向量法
若二面角 两个半平面
两个半平面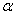 ,
,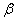 的法向量分别为
的法向量分别为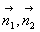 且知道二面角
且知道二面角 为锐角(钝角),则
为锐角(钝角),则
 .
.
例12 如图15,在矩形ABCD外存在一点P,使PA^面ABCD,PA=PB=1,BC=2.求二面角B-PC-D的大小.
解:由题意建立如图空间直角坐标系,则A(0,0,0) P(0,0,1) B(1,0,0) C(1,2,0) D(0,2,0),设面PAC的法向量为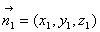 ,
,
 面PCD的法向量
面PCD的法向量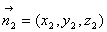
则有
由 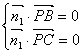
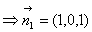
及 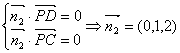
得

注意到B-PC-D为钝角,故B-PC-D的大小为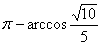 .
.
2.2.3 距离公式法
 2.2.3.1结论1
2.2.3.1结论1
如果二面角 的夹角为锐角(钝角),
的夹角为锐角(钝角),
(如图16)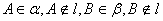
作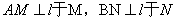 则异面直线AM,BN
则异面直线AM,BN
的夹角与二面角的平面角相等(互补).
2.2.3.2 异面直线两点间距离公式
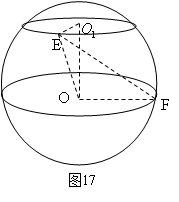
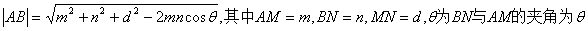 例13
例13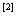 如图17,点E在北纬
如图17,点E在北纬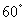 ,东经
,东经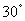 处,点
处,点
F在赤道上,且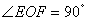 ,问点F在东经多少度?
,问点F在东经多少度?
解:由题意可知,本题关键在求二面角
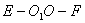 的大小,设地球半径为1即OE=OF=1,易知
的大小,设地球半径为1即OE=OF=1,易知
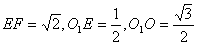 ,
,
由公式
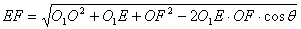
得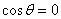 .故二面角
.故二面角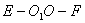 平面角为
平面角为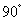 .
.
由题意可知F在东经 处.
处.
3.2.4向量法
在3.2.3.1中结论1可以进一步引用向量的方法解决
定理1 设二面角 为
为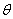 ,
,
 ,则,有
,则,有
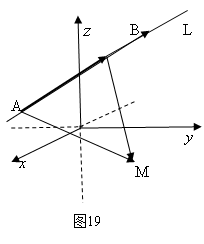
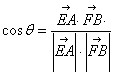
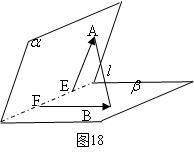
文 给出另一结论:
给出另一结论:
定理 2 如图19,空间任一条直线L,A,B是直线L上的两个点,M是空间
任一点,MN^L于N,则
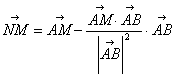
利用上述两结论我们可以利用空间坐标向量计算二面角,避免产生二面角的
平面角与其法向量夹角的误判,同时又避免了对垂足M,N坐标的判断.
 例14
例14 如图20,已知正方形ABCD和矩形ACEF坐在平面相垂直,
如图20,已知正方形ABCD和矩形ACEF坐在平面相垂直, ,M是线段EF中点,求二面角A-DF-B的大小.
,M是线段EF中点,求二面角A-DF-B的大小.
解: 如图建立空间直角坐标系
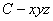 ,则
,则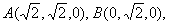
 .
.
作AM^DF于M,BN^DF的延长线于N,则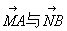 所成的角
所成的角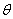 的大小与二面角A-DF-B的大小相等.
的大小与二面角A-DF-B的大小相等.
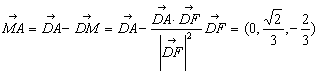
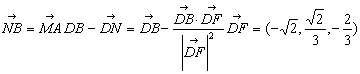
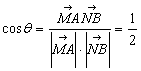
故二面角A-DF-B的大小为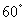 .
.
2.2.5 正三弦公式法
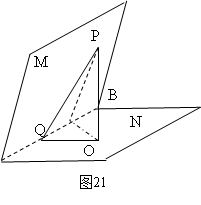 如图21所示,二面角M-AB-N中,PQ与AB所成的角为
如图21所示,二面角M-AB-N中,PQ与AB所成的角为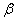 ,PQ与面N所
,PQ与面N所
成的角为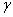 ,二面角M-AB-N为
,二面角M-AB-N为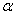 ,则有
,则有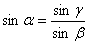 .
.
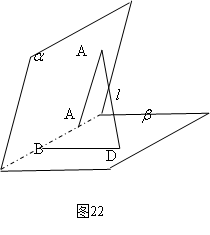
例15 如图22,在二面角 的棱上P在
的棱上P在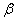 内引一条直线PC,PC与
内引一条直线PC,PC与
棱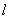 成
成 角,与平面
角,与平面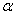 成
成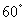 角,则二面角
角,则二面角 的大小为
的大小为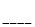
解:可以直接利用公式进行求解
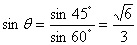
故可知二面角 的大小为
的大小为 .
.
2.2.6 构造面积公式
如图23在三棱锥P-ABC中,PA,PB,PC两两相互垂直,设

二面角A-BC-P为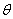 ,则有
,则有
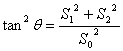
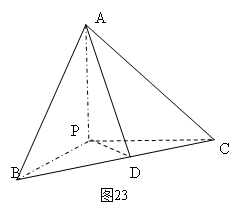
例16 如图15,在矩形ABCD外存在一点P,使PA^面ABCD,PA=PB=1,BC=2.求二面角B-PC-D的大小.
如图15,在矩形ABCD外存在一点P,使PA^面ABCD,PA=PB=1,BC=2.求二面角B-PC-D的大小.
解: 如图24,过E作EF^FD,垂足为F,过F作FG^PD交PC于G,连EG,
可证FP,PE,FG两两垂直,不难求得
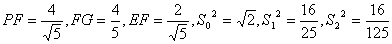
设二面角B-PC-D的大小为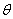 ,则,有
,则,有
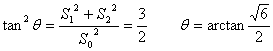
故二面角B-PC-D的大小为 .
.


小结
评注:本文给出了二面角的相关求法以及一些例题,对于二面角的解题策略按照求作二面角的平面角和无需定位二面角的平面角两种思路来分别加以介绍.本文试图按照这两种思路分二面角的两种题型加以说明概括.
这13种方法动用了数学上的集中解题思想:转化思想、类比思想、建构图像思想、将维思想等,下对以上这些方法和思想进一步加以归类,以便于后来者研究和总结.


