第四章 圆与方程
1、圆的定义:平面内到一定点的距离等于定长的点的集合叫圆,定点为圆心,定长为圆的
半径。
2
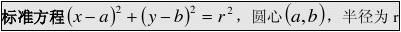
(1222 点M(x0,y0)与圆(x?a)?(y?b)?r的位置关系:
当(x0?a)?(y0?b)>r2,点在圆外
当(x0?a)?(y0?b)=r2,点在圆上
2当(x0?a)
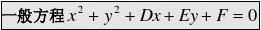
?(y0?b)<r,点在圆内 222222
(21DE?,半径为当D?E?4F?0时,方程表示圆,此时圆心为?r?D2?E2?4F ??,???22?2
?E2?4F?0时,表示一个点;
22当D?E?4F?0时,方程不表示任何图形。 当D
(3)求圆方程的方法:
一般都采用待定系数法:先设后求。确定一个圆需要三个独立条件,若利用圆的标准方程, 需求出a,b,r;若利用一般方程,需要求出D,E,F;
另外要注意多利用圆的几何性质:如弦的中垂线必经过原点,以此来确定圆心的位置。
3、直线与圆的位置关系:
直线与圆的位置关系有相离,相切,相交三种情况:
(1)设直线l:Ax?By?C?0,圆C:?x?a?2??y?b?2?r2,圆心C?a,b?到l的距离

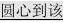
则有d?r?l与C相离
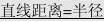
;d?r?l与C相切;d?r?l与C相交
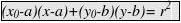
:①k不存在,验证是否成立②kk,得到方程【一定两解】
圆(x-a)2+(y-b)2=r2,圆上一点为(x0,y0),则过此点的切线方程为
4、圆与圆的位置关系:通过两圆半径的和(差),与圆心距(d)之间的大小比较来确定。
22设圆C1:?x?a1?2??y?b1?2?r2,C2:?x?a2???y?b2??R2
两圆的位置关系常通过两圆半径的和(差),与圆心距(d)之间的大小比较来确定。 2
当
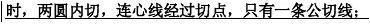
d?R?
当
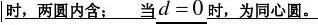
d?R?


注意:已知圆上两点,圆心必在中垂线上;已知两圆相切,两圆心与切点共线 圆的辅助线一般为连圆心与切线或者连圆心与弦中点
圆的方程
基础自测
1.方程x+y+ax+2ay+2a+a-1=0表示圆,则a的取值范围是 ( ) A.a<-2或a>C.-2<a<0 答案D
2.(2009·河南新郑模拟)圆x+y+2x-4y+1=0关于直线2ax-by+2=0(a、b∈R)对称,则ab的取值范围
是
( )
2
2
2
2
2
2 3
B.-
2
<a<0 3
2 3
D.-2<a<
1??
A.????
4??答案A
?1?
B.?0? ?4?
?1?
C.??,0? ?4?
1??
D.???,?
4??
( )
3.过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是 A.(x-3)+(y+1)=4 C.(x-1)+(y-1)=4 答案C
4.以点(2,-1)为圆心且与直线3x-4y+5=0相切的圆的方程为 A.(x-2)+(y+1)=3 C.(x-2)+(y+1)=9 答案C
2
2
2
2
2
2
2
2
B.(x+3)+(y-1)=4 D.(x+1)+(y+1)=4
222
2
22
2
( )
B.(x+2)+(y-1)=3
D.(x+2)+(y-1)=9
2
2
2
2
5.(2009·宜昌模拟)直线y=ax+b通过第一、三、四象限,则圆(x+a)+(y+b)=r (r>0)的圆心位于( )A.第一象限 C.第三象限

答案B
B.第二象限
D.第四象限
例1 已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )A.x+y-2x-3=0 C.x+y+2x-3=0 答案D
2
22
2
2
2
B.x+y+4x=0
2
2
D.x+y-4x=0
例2 已知圆x+y+x-6y+m=0和直线x+2y-3=0交于P,Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
解 方法一 将x=3-2y,
代入方程x+y+x-6y+m=0,得5y-20y+12+m=0.
设P(x1,y1),Q(x2,y2),则y1、y2满足条件:y1+y2=4,y1y2=
∵OP⊥OQ,∴x1x2+y1y2=0.而x1=3-2y1,x2=3-2y2.
∴x1x2=9-6(y1+y2)+4y1y2.
5?1?∴m=3,此时Δ>0,圆心坐标为??,3?,半径r=. 2?2?2222212?m. 5
方法二 如图所示,设弦PQ中点为M,
∵O1M⊥PQ,∴kO1M1???2.∴O1M的方程为:y-3=2?x??, 2??
?y?2x?4即:y=2x+4.由方程组?. x?2y?3?0?
解得M的坐标为(-1,2).
则以PQ为直径的圆可设为(x+1)+(y-2)=r.
∵OP⊥OQ,∴点O在以PQ为直径的圆上.
∴(0+1)+(0-2)=r,即r=5,MQ=r.
在Rt△O1MQ中,O1Q=O1M+MQ. 222222222222
1?(?6)2?4m?1?2∴???1??(3-2)+5= 4?2?
∴m=3.∴半径为5?1?,圆心为??,3?. 2?2?2
方法三 设过P、Q的圆系方程为
x+y+x-6y+m+?(x+2y-3)=0.由OP⊥OQ知,点O(0,0)在圆上.
∴m-3?=0,即m=3?.
∴圆的方程可化为x+y+x-6y+3?+?x+2?y-3?=0即x+(1+?)x+y+2(?-3)y=0. 222222
?1??2(3??)?∴圆心M???,又圆在PQ上. 22??
∴-1??5?1?+2(3-?)-3=0,∴?=1,∴m=3.∴圆心为??,3?,半径为. 22?2?
22例3 (12分)已知实数x、y满足方程x+y-4x+1=0.
(1)求y-x的最大值和最小值;
(2)求x+y的最大值和最小值.

22
解 (1)y-x可看作是直线y=x+b在y轴上的截距,当直线y=x+b与圆相切时,纵截距b取得最大值或最小值,此时2?0?b
2?3,,解得b=-2±6. 5分
所以y-x的最大值为-2+6,最小值为-2-6.
22 6分 (2)x+y表示圆上的一点与原点距离的平方,由平面几何知识知,在原点与圆心连线与圆的两个交点处取得最大值和最小值.
又圆心到原点的距离为2?0)2?(0?0)2=2,
所以x2+y2的最大值是(2+3)2=7+4,
x2+y2的最小值是(2-3)2=7-43.
圆与直线方程
例1 已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).
(1)求证:不论m为何值,圆心在同一直线l上;
(2)与l平行的直线中,哪些与圆相交、相切、相离;
(3)求证:任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
(1)证明 配方得:(x-3m)2+[y-(m-1)]2=25,
设圆心为(x,y),则??x?3m,消去
?y?m?1m得
l:x-3y-3=0,则圆心恒在直线l:x-3y-3=0上.
(2)解 设与l平行的直线是l1:x-3y+b=0,则圆心到直线l1的距离为
d=m?3(m?1)?b3?b
?.
∵圆的半径为r=5,
∴当d<r,即-5-3<b<5-3时,直线与圆相交;
当d=r,即b=±5-3时,直线与圆相切; 8分 12分
当d>r,即b<-5-3或b>5-3时,直线与圆相离.
(3)证明 对于任一条平行于l且与圆相交的直线l1:x-3y+b=0,由于圆心到直线l1的距离d=3?b
(4)弦长=2r2?d2且r和d均为常量.
∴任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
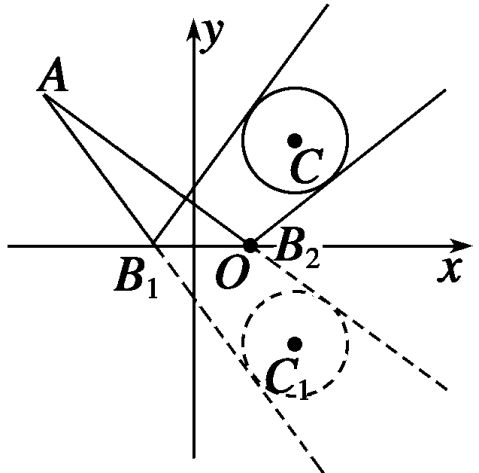
例2 从点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x+y-4x-4y+7=0相切,求光线l所在直线的方程.
解 方法一 如图所示,设l与x轴交于点B(b,0),则kAB=
反射光线的斜率k反=
2222?3,根据光的反射定律, b?333.∴反射光线所在直线的方程为y=(x-b),即3x-(b+3)y-3b=0. b?3b?3∵已知圆x+y-4x-4y+7=0的圆心为C(2,2),半径为1, ∴6?(b?3)?2?3b
9?(b?3)2=1,解得b1=-3,b2=1. 4
∴kAB=-34或kAB=-.∴l的方程为4x+3y+3=0或3x+4y-3=0. 43
2222方法二 已知圆C:x+y-4x-4y+7=0关于x轴对称的圆为C1:(x-2)+(y+2)=1,其圆心C1的坐标为(2,
-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切.
设l的方程为y-3=k(x+3),则
∴k1=-5k?5?k22=1,即12k+25k+12=0. 234,k2=-.则l的方程为4x+3y+3=0或3x+4y-3=0. 43
方法三 设入射光线方程为y-3=k(x+3),反射光线所在的直线方程为y=-kx+b,由于二者横截距相等,且后者与已知圆相切. ??3?3kb??kk5k?534?2,消去b得∴?=1.即12k+25k+12=0,∴k1=-,k2=-. 2k?2?b43?k2??12???k
则l的方程为4x+3y+3=0或3x+4y-3=0.
例3 已知圆C1:x+y-2mx+4y+m-5=0,圆C2:x+y+2x-2my+m-3=0,m为何值时,
(1)圆C1与圆C2相外切;(2)圆C1与圆C2内含?
解 对于圆C1与圆C2的方程,经配方后
C1:(x-m)+(y+2)=9; C2:(x+1)+(y-m)=4.
(1)如果C1与C2外切,则有m?1)2?(m?2)2=3+2.
(m+1)+(m+2)=25.m+3m-10=0,解得m=-5或m=2.
(2)如果C1与C2内含,则有m?1)2?(m?2)2<3-2.
(m+1)+(m+2)<1,m+3m+2<0,得-2<m<-1,
∴当m=-5或m=2时,圆C1与圆C2外切;
当-2<m<-1时,圆C1与圆C2内含.
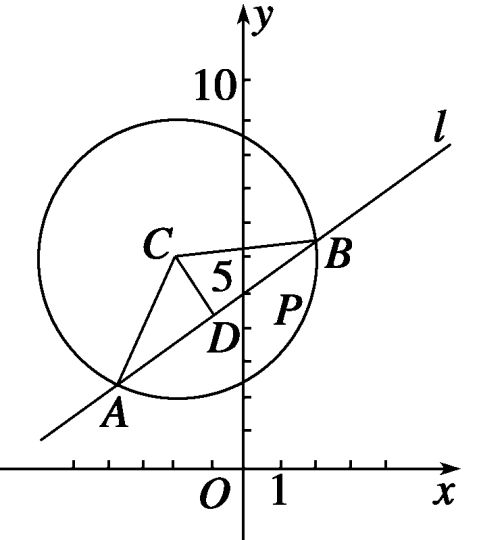
例4(12分)已知点P(0,5)及圆C:x+y+4x-12y+24=0.
(1)若直线l过P且被圆C截得的线段长为43,求l的方程;
(2)求过P点的圆C的弦的中点的轨迹方程.
22解 (1)方法一 如图所示,AB=4,D是AB的中点,CD⊥AB,AD=23,圆x+y+4x-12y+24=0可222222222222222222
化为(x+2)+(y-6)=16,圆心C(-2,6),半径r=4,故AC=4,
在Rt△ACD中,可得CD=2. 2分
设所求直线的斜率为k,则直线的方程为y-5=kx
, 22
即kx-y+5=0.
由点C到直线AB的距离公式:
?2k?6?5k2?(?1)2
=2,得k=
3. 4
此时直线l的方程为3x-4y+20=0.
4分 6分
又直线l的斜率不存在时,此时方程为x=0. 则y2
-12y+24=0,∴y1=6+23,y2=6-2, ∴y2-y1=43,故x=0满足题意. ∴所求直线的方程为3x-4y+20=0或x=0.
方法二 设所求直线的斜率为k,则直线的方程为y-5=kx,即y=kx+5, 联立直线与圆的方程??y?kx?5
?
x2?y2
?4x?12y?24?0, 消去y得(1+k2)x2
+(4-2k)x-11=0
①?
x2k?41?x2?设方程①的两根为x,由根与系数的关系得??1,x2?1?k2
???
x1x2??
111?k2由弦长公式得?k2|x1-x2|=1?k2)[(x1?x2)2?4x1x2]?43, 将②式代入,解得k=
3
4
,此时直线的方程为3x-4y+20=0. 又k不存在时也满足题意,此时直线方程为x=0. ∴所求直线的方程为x=0或3x-4y+20=0.
(2)设过P点的圆C的弦的中点为D(x,y),则CD⊥PD,即·=0, (x+2,y-6)·(x,y-5)=0,化简得所求轨迹方程为x2
+y2
+2x-11y+30=0.
3.求过点P(4,-1)且与圆C:x2
+y2
+2x-6y+5=0切于点M(1,2)的圆的方程.
解 方法一 设所求圆的圆心为A(m,n),半径为r, 则A,M,C三点共线,且有|MA|=|AP|=r,
因为圆C:x2
+y2
+2x-6y+5=0的圆心为C(-1,3),
8分2分
② 4分 8分
?n?22?3??则?m?11?1,
?(m?1)2?(n?2)2?(m?4)2?(n?1)2?r?
解得m=3,n=1,r=5,
所以所求圆的方程为(x-3)+(y-1)=5.
方法二 因为圆C:x+y+2x-6y+5=0过点M(1,2)的切线方程为2x-y=0,
所以设所求圆A的方程为
x+y+2x-6y+5+?(2x-y)=0,
因为点P(4,-1)在圆上,所以代入圆A的方程,
解得?=-4,
所以所求圆的方程为x+y-6x-2y+5=0.
4.(2008·全国Ⅰ文,10)若直线
A.a+b≤1
答案D
5.能够使得圆x+y-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c的一个值为 ( ) A.2 B. C.3 D.35 222222222222xy22?=1与圆x+y=1有公共点,则 ab22 D. ( ) B.a+b≥1 C.11≤1 ?a2b211≥1 ?a2b2答案C
第二篇:方程与方程组知识点总结及习题
方程与方程组
一.一元一次方程:在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫一元一次方程。
解一元一次方程的步骤:去分母,移项,合并同类项,未知数系数化为1。
二.二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
二元一次方程组:两个二元一次方程组成的方程组叫做二元一次方程组。 适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解。
二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解。 解二元一次方程组的方法:代入消元法/加减消元法。
三.一元二次方程:只有一个未知数,并且未知数的项的最高系数为2的方程 1 韦达定理
韦达定理就是在一元二次方程中,二根之和=-b/a,二根之积=c/a,也可以表示为x1+x2=-b/a,x1x2=c/a。它描述了根与系数的关系,在题目中很常用。 2 一元二次方程根的情况
利用根的判别式去了解根的分布情况,而△=b2-4ac,这里可以分为3种情况:
I 当△>0时,一元二次方程有2个不相等的实数根;
II 当△=0时,一元二次方程有2个相同的实数根;
III 当△<0时,一元二次方程没有实数根
3 一元二次方程的解法
(1)配方法
利用配方,使方程变为完全平方公式,在用直接开平方法去求出解 配方法的步骤:
先把常数项移到方程的右边,再把二次项的系数化为1,再同时加上1次项的系数的一半的平方,最后配成完全平方公式
(2)分解因式法
提取公因式,和十字相乘法。利用这点,把方程化为几个乘积的形式去解 分解因式法的步骤:
把方程右边化为0,然后看看是否能用提取公因式,公式法(这里指的是分解因式中的公式法)或十字相乘(利用根与系数的关系),如果可以,就可以化为乘积的形式
a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b(a2+ab+b2)
(3)公式法
这

以是在解一元二次方程的万能方法了,方程的根?b?X? 2a公式法的步骤:
就把一元二次方程的各系数分别代入,这里二次项的系数为a,一次项的系数为b,常数项的系数为c
一元一次方程
1.在①2x?1;②2x?1?3x;③π?3?π?3;④t?1?3中,等式有_______,方程有_______.(填入式子的序号)
2 某书店按标价的八折售出,仍可获利20﹪,若该书的进价为18元,则标价为( )
A. 27元 B. 28元 C. 29元 D,30元
3 小明把400元钱存入银行,年利率为1.8%,到期时小明得到利息36元,则她一共存了( )
A、6年 B、5年 C、4年 D、3年
4.求方程 3x+3 ? 1 1 6 ·? x-1 x+1 ÷ x =+1 x
5.(7分)去年入秋以来,云南省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务. 问原计划每天修水渠多少米?
二元一次方程组
6若方程(m?2)x
=___。
7方程组?
?2x?3y?k8已知关于x、y的方程组?的解的和是12,则k?_______。 3x?2y?k?2??3x?4y?7?ax?2y?10|m?1|?(n?3)yn?8?0是关于x、y的二元一次方程,则m=___,n的解x、y满足关系式y??x,则a=______________。
?2(x?y)?3(x?y)?139 ? 3x?y?2x?y?13?????
10.(8分)某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标
价如下表所示.

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
11、现有两种酒精溶液,甲种酒精溶液的浓度为30%,乙种酒精的浓度为80%,今要得到
浓度为50%的酒精溶液50千克,问甲、乙两种酒精溶液各取多少?
一元二次方程
12.方程y2?a?0的根是 ( )
(A
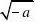
)(B)无解; (C)0; (D
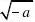
).
13.方程(x?1)(x?3)?1的两个根是 ( )
(A)x1?1,x2?3; (B)x1?2,x2?4;
(C
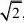
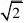
)x1?2?x2?2?(D
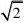
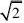
)x1??2?x2??2?14.如果二次三项式mx2?5x?7在实数范围内不能分解因式,那么m的取值范围是 ( )
(A)m?25
28; (B)m?0;
28
25,且m?0; (D)m?5
7,且m?0. (C)0?m?
15.已知关于x的方程x2?mx?5?0的一个根是5,那么m= .
16.因式分解:x2?1?2x?17.已知3x?x?1的值为2,则9x?3x?1的值为18.某工厂在第一季度的生产中,一月份的产值为150万元,二、三月份产值的月增长率相同.已知第一季度的总产值是650万元,求二、三月份的月增长率?现设二、三月份的月增长率为x,则根据题意可列出方程 .
19.已知关于x的方程m?m2?1?x2?mx?3?m?0有实根,求m的值.
20.关于x的一元二次方程(k?4)x?2x?1?0: (1)若方程有两个不相等的实数根,则k的取值范围; (2)当k是怎样的正整数时,方程没有实数根.
21.已知x为实数,且(x?2x)(x?2x?1)?6,求x的值.
22.已知三角形的边长1和2,第三边长为0.09y?0.21y?0.1?0的根,求这个三角形的周长. 222222
