第四章 圆与方程知识点
1. ★1、圆的定义:平面内到一定点的距离等于定长的点的集合叫做圆,定点为圆心,定长为圆的半径。
设M(x,y)为⊙A上任意一点,则圆的集合可以写作:P = {M | |MA| = r }
★2、圆的方程
(1)标准方程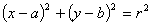 ,圆心
,圆心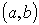 ,半径为r;
,半径为r;
点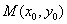 与圆
与圆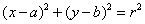 的位置关系:
的位置关系:
当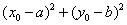 >
>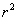 ,点在圆外; 当
,点在圆外; 当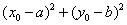 =
=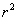 ,点在圆上
,点在圆上
当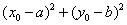 <
<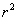 ,点在圆内;
,点在圆内;
(2)一般方程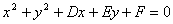
(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4 (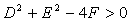 )
)
当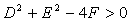 时,方程表示圆,此时圆心为
时,方程表示圆,此时圆心为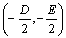 ,半径为
,半径为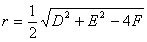
当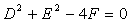 时,表示一个点;
时,表示一个点;
当 时,方程不表示任何图形。
时,方程不表示任何图形。
(3)求圆的方程的方法:
?待定系数法:先设后求。确定一个圆需要三个独立条件,若利用圆的标准方程,
需求出a,b,r;若利用一般方程,需要求出D,E,F;
?直接法:直接根据已知条件求出圆心坐标以及半径长度。
另外要注意多利用圆的几何性质:如弦的中垂线必经过圆心,以此来确定圆心的位置。
★3、直线与圆的位置关系:
直线与圆的位置关系有相离,相切,相交三种情况:
(1)设直线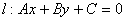 ,圆
,圆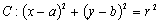 ,圆心
,圆心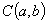 到l的距离为
到l的距离为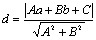 ,则有
,则有 ;
; ;
;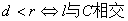
(2)过圆外一点的切线:设点斜式方程,用圆心到该直线距离=半径,求解k,
①若求得两个不同的解,带入所设切线的方程即可;
②若求得两个相同的解,带入切线方程,得到一条切线;接下来验证过该点的斜率不存在的直线(此 时,该直线一定为另一条切线)
(3) 过圆上一点的切线方程:圆(x-a)2+(y-b)2=r2,圆上一点为(x0,y0),则过此点的切线方程为(x0-a)(x-a)+(y0-b)(y-b)= r2

★4、圆与圆的位置关系:通过两圆半径的和(差),与圆心距(d)之间的大小比较来确定。
设圆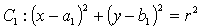 ,
,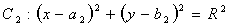
两圆的位置关系常通过两圆半径的和(差的绝对值),与圆心距(d)之间的大小比较来确定。(即几何法)
注意:已知圆上两点,圆心必在中垂线上;已知两圆相切,两圆心与切点共线
★5、.圆C1:x2+y2+D1x+E1y+F1=0 圆C2:x2+y2+D2x+E2y+F2=0
联立圆C1的方程与圆C2的方程得到一个二元一次方程
① 若两圆相交,则该二元一次方程表示:圆C1与圆C2公共弦所在的直线方程;
② 若两圆相切,则该二元一次方程表示:圆C1与圆C2的公切线的方程;
③ 若两圆外离,则该二元一次方程表示的直线具有一个性质:从直线上任意一点向两个圆引切线, 得到的切线长相等(反之,亦成立)
★6、已知一直线与圆相交,求弦的长度
①代数法:联立圆与直线的方程求出交点坐标,利用两点间的距离公式求弦长
②几何法:半弦长、弦心距、半径构成直角三角形(勾股定理)
③代数法:直线方程与圆的方程联立,消去一个未知数,得到一个一元二次方程;利用弦长公式:
|AB|=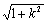
 |x1-x2| (或者|AB|=
|x1-x2| (或者|AB|=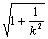
 |y1-y2|)求解
|y1-y2|)求解
★7、已知两圆相交,求公共弦的长度
①代数法:联立两圆的方程求出交点坐标;利用两点间的距离公式求弦长
②代数法:联立两圆的方程求出公共弦所在直线的方程(设公共弦的端点分别为A、B);公共弦直线方程 与任一圆的方程联立,消去一个未知数,得到一个一元二次方程;利用弦长公式:
|AB|=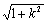
 |x1-x2| (或者|AB|=
|x1-x2| (或者|AB|=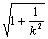
 |y1-y2|)求解
|y1-y2|)求解
③几何法:半弦长、弦心距、半径构成直角三角形(勾股定理)
④几何法:根据图像求解(两个直角三角形,两个未知数,解二元一次方程组)
★8、圆系与圆系方程
(1) 圆系:具有某种共同属性的圆的集合,称为圆系。
(2) 圆系方程:
(一).圆C1:x2+y2+D1x+E1y+F1=0 圆C2:x2+y2+D2x+E2y+F2=0
圆系方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 (λ≠-1) -- (Ⅰ)
①若圆 C1与圆C2交于P1、P2点,那么,方程(Ⅰ)代表过P1、P2两点的圆的方程。
②若圆 C1与圆C2交于P点(一个点),则方程(Ⅰ)代表与圆C1 、圆C2相切于P点的圆的方程。
(二).直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0相交或相切
则过它们的交点的圆系方程为:x2+y2+Dx+Ey+F+λ(Ax+By+C)=0
★9、直线与圆的方程的应用
用坐标法解决平面几何问题的“三部曲”:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论
、
第二篇:高中数学知识点总结_曲线与方程,圆的方程
曲线与方程、圆的方程
1.曲线C的方程为:f(x,y)=0?曲线C上任意一点P(x0,y0)的坐标满足方程f(x,y)=0,即f(x0,y0)=0;且以f(x,y)=0的任意一组解(x0,y0)为坐标的点P(x0,y0)在曲线C上。 依据该定义:已知点在曲线上即知点的坐标满足曲线方程;求证点在曲线上也只需证点的坐标满足曲线方程。求动点P(x,y)的轨迹方程即求点P的坐标(x,y)满足的方程(等式)。求动点轨迹方程的步骤:①建系,写(设)出相关点的坐标、线的方程,动点坐标一般设为(x,y),②分析动点满足的条件,并用等式描述这些条件,③化简,④验证:满足条件的点的坐标都是方程的解,且以方程的解为坐标的点都满足条件。
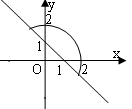
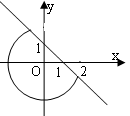
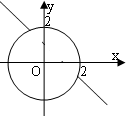
[举例1] 方程(x?y?1)x2?y2?4?0所表示的曲线是: ( )
A B C D ?x?y?1?022
解析:原方程等价于:?2,或x?y?4; 2
?x?y?4
其中当x?y?1?0需x?y?4有意义,等式才成立,即x?y
2222
?4,此时它表示直
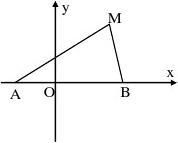
线x?y?1?0上不在圆x2?y2?4内的部分,这是极易出错的一个环节。选D。 [举例2] 已知点A(-1,0),B(2,0),动点M满足2∠MAB=∠MBA,求点M的轨迹方程。 解析:如何体现动点M满足的条件2∠MAB=∠MBA
是解决本题的关键。用动点M的坐标体现2∠MAB=∠MBA 的最佳载体是直线MA、MB的斜率。 设M(x,y),∠MAB=?,则∠MBA=2?,它们是直线
MA、MB的倾角还是倾角的补角,与点M在x轴的上方
还是下方有关;以下讨论:
① 若点M在x轴的上方, ??(00,900),y?0, 此时,直线MA的倾角为?,MB的倾角为?-2?,
?tan??kMA?
yx?1
,tan(??2?)?
yx?2
, (2??900)
2?
?
1?
yx?1
2y
2
?tan(??2?)??tan2?,??
yx?2
,
(x?1)
得: x?
2
y
2
3
?1,∵MA?MB,?x?1.
当2??900时, ?=450,?MAB为等腰直角三角形,此时点M的坐标为(2,3),它满足上述
方程.
②当点M在x轴的下方时, y<0,同理可得点M的轨迹方程为x?2y2
3?1(x?1),
③当点M在线段AB上时,也满足2∠MAB=∠MBA,此时y=0(-1<x<2). 综上所求点的轨迹方程为x?2y2
3?1(x?1)或y?0(?1?x?2).
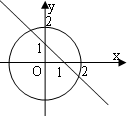
[巩固1]右图的曲线是以原点为圆心,1为半径的圆的一部分,
则它的方程是
A.(x??y2)·(y??x2)=0
B.(x??y2)·(y??x2)=0
C.(x??y2)·(y??x2)=0
D.(x??y2)·(y??x2)=0
[巩固2]已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足RP·PM=0,2PM+3MQ=0,当点P移动时,求M点的轨迹方程。
[迁移]正方体ABCD-A1B1C1D1的棱长为1,点M是棱AB的中点,点P是平面ABCD上的一动点,且点P到直线A1D1的距离两倍的平方比到点M的距离的平方大4,则点P的轨迹为: A.圆 B.椭圆 C.双曲线 D.抛物线
2.圆的标准方程刻画了圆的位置特点(圆心与半径),圆的一般方程反映了圆的代数特点(二元二次方程Ax2+By2+Cxy+Dx+Ey+F=0?A=B≠0,C=0,且D2+E2-4AF>0)。判断点P(x0,y0)与⊙M:(x-a)2+(y-b)2= r2的位置关系,用|PM|与r的大小,即:|PM|>r?(x0-a)2+(y0-b)2> r2?P在⊙M外;|PM|<r?(x0-a)2+(y0-b)2< r2?P在⊙M内;|PM|=r?(x0-a)2+(y0-b)2= r2?P在⊙M上。过两个定点A、B的圆,圆心在线段AB的中垂线上。
[举例1]一圆经过A(4,2),B(-1,3)两点,且在两坐标轴上的四个截距之和为2,则圆的方程为 。
解析:研究圆在坐标轴上的截距,宜用一般方程(因为与圆心、半径没有直接联系),设圆的方程为x2+y2+Dx+Ey+F=0,∵圆过点A、B,∴4D+2E+F+20=0 ①,-D+3E+F+10=0 ②, 圆在x轴上的截距即圆与x轴交点的横坐标,当y=0时,x2+Dx+F=0,x1+x2=-D
圆在y轴上的截距即圆与y轴交点的纵坐标,当x=0时,y2+Ey+F=0,y1+y2=-E
由题意知:-D-E=2 ③,解①②③得D=-2,E=0,F=-12。
[举例2]若存在实数k使得直线l:kx-y-k+2=0与圆C:x2+2ax+y2-a+2=0无公共点,则实数a的取值范围是: 。
解析:本题看似直线远的位置关系问题,其实不然。注意到直线l对任意的实数k恒过定点 M(1,2),要存在实数k使得直线l与⊙C相离,当且仅当M点在圆外;方程x2+2ax+y2-a+2=0
22222变形为:(x+a)+y= a+a-2, M点在⊙C外?(1+a)+4>a+a-2>0,解得:-7<a<-2或a>1.
注:本题中a2+a-2>0是极易疏漏的一个潜在要求。
[巩固1]过点A(3,-2),B(2,1)且圆心在直线x-2y-3=0上的圆的方程是 。
[巩固2]已知定点M(x0,y0)在第一象限,过M点的两圆与坐标轴相切,它们的半径分别为r1, r2,则r1r2= 。
[迁移] 关于曲线C:x4?y2?1给出下列说法:①关于直线y?0对称;②关于直线x?0对称;③关于点(0,0)对称;④关于直线y?x对称;⑤是封闭图形,面积小于?;⑥是封闭图形,面积大于?;则其中正确说法的序号是
3.涉及直线与圆的位置关系的问题,宜用圆心到直线的距离d来研究。d=r(r为圆的半径)?直线与圆相切;过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2;过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点A、B连线的直线方程为x0x+y0y=r。过⊙A外一点P作圆的切线PQ(Q为切点),则|PQ|=PA|2?r2。d<r?直线与圆相交,弦长|AB|=2r?d222;过直线Ax+By+C=0与圆:x2?y2?Dx?Ey?F=0的交点的圆系方程:x2?y2?Dx?Ey?F+?(Ax+By+C)=0 。d>r?直线与圆相离,圆周上的点到直线距离的最小值为d-r,最大值为d+r。
[举例1] 从直线x-y+3=0上的点向圆(x?2)2?(y?2)2?1引切线,则切线长的最小值是 32
22324322A. B. C. D. -1
解析:圆(x?2)2?(y?2)2?1的圆心A(-2,-2),直线x-y+3=0上任一点P,过引圆的切线PQ(Q为切点),则|PQ|=|PA|2?1,当且仅当|PA|最小时|PQ|最小,易见|PA|的最
32
22小值即A到直线x-y+3=0的距离,为,此时|PQ|=,选B。
[举例2] 能够使得圆x?y?2x?4y?1?0上恰有两个点到直线2x?y?c?0距离等于1的c的一个值为:A.2
C.3 D
.解析:本题如果设圆上一点的坐标,用点到直线的距离公式得到一个方程,进而研究方程解的个数,将是非常麻烦的。注意到圆心M(1,-2),半径r=2,结合图形容易知道,当且仅当M到直线l:2x?y?c?0的距离d∈(1,3)时,⊙M上恰有两个点到直线l的距离
|c|
522等于1,由d=∈(1,3)得:c?(?35,?5)?(5,35),选C。
[巩固1] 若直线(1+a)x+y+1=0与圆x2+y2-2x=0相切,则a的值为 ( )
(A)1,-1 (B)2,-2 (C)1 (D)-1
[巩固2]直线l1:y=kx+1与圆C:x+y+2kx+2my=0的两个交点A、B关于直线l2:x+y=0对称,则CA?CB= 。 22
[迁移]实数x,y满足x2?y2?2x?2y?1?0,则 A.[,??)
34
y?4x?2
的取值范围为
43]
( )
43,0)
B.[0,]
3
4
C.(??,?D.[?
4.判断两圆的位置关系用圆心距与它们半径和、差的大小。⊙M、⊙N的半径分别为r1、r2, |MN|>r1+r2?外离,|MN|=r1+r2?外切,|r1-r2|<|MN|<r1+r2?相交,此时,若⊙M: ⊙N:x?y?D2x?E2y?F2?0,过两圆交点的圆(系)x?y?D1x?E1y?F1?0,
的方程为:x2?y2?D1x?E1y?F1+?(x2?y2?D2x?E2y?F2)=0(⊙N除外)。 特别地:当?= -1时,该方程表示两圆的公共弦。连心线垂直平分公共弦。|MN|=|r1-r2|?内切,|MN|<|r1-r2|?内含。
[举例1]已知两圆O1:x+y=16,O2:(x-1)+(y+2)=9,两圆公共弦交直线O1O2于M点,则
O1分有向线段MO2所成的比λ= ( ) A.
65
2
2
2
2
2
2
2
2
B.
56
C.-
65
65
D.-,?
56
),有定比分点
解析:直线O1 O2:y= -2x,两圆公共弦:x-2y=6,于是有:M(坐标公式不难得到λ的值,选C。
125
[举例2] 若A?{(x,y)|x2?y2?16},B?{(x,y)|x2?(y?2)2?a?1}且A?B?B, 则a的取值范围是
( )
A.a?1 B.a?5 C.1?a?5 D.a?5 解析:集合A、B分别表示两个圆面(a=1时集B表示一个点),A∩B=B?B?A,即两圆内含;有两圆圆心分别为原点和(0,2),半径分别为4和a?1,于是有:2≤4-a?1,解得:1?a?5,选C。
[巩固1]圆心在直线x?y?4?0上,且经过两圆x2?y2?4x?3?0,x2?y2?4y?3?0的交点的圆的方程为
2
2
2
2
( )
A.x?y?6x?2y?3?0
C.x?y?6x?2y?3?0
2
2
B.x?y?6x?2y?3?0 D.x?y?6x?2y?3?0
2
2
[巩固2]若圆(x-a)2+(y-b)2=6始终平分圆x2+y2+2x+2y-3=0的周长,则动点M(a,b)的轨迹方程是
A.a2+b2-2a-2b+1=0 C.a2+b2-2a+2b+1=0
B.a2+b2+2a+2b+1=0 D.a2+b2+2a-2b+1=0
[迁移]与圆x2+y2?2x=0外切且与y轴相切的动圆圆心的轨迹方程为 。
5.圆的参数方程的本质是sin2?+ cos2?=1。参数方程的重要用途是设圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系。
[举例]已知圆x2?(y?1)2?1上任意一点P(x、y)都使不等式x+y+m?0成立,则m的取值范围是:A .[2?1,??) B ???,0? C (2,??) D [1? 2,??) ( )解析:不等式x+y+m?0恒成立?m? -(x+y)恒成立,以下求-(x+y)的最大值: 记x= cos?、y=1+ sin?,-(x+y)= -( cos?+1+ sin?)= -1-2sin(?+
sin?
2?cos??4)≤-1+2,选A。 [巩固1] f(?)?的最大值为。
a
b34[巩固2]在⊿ABC中,已知
+PC的最大值为 2cosBcosA??,c=10,P是⊿ABC的内切圆上一点,则PA2+PB2
[迁移]动点P,Q坐标分别为p?cos?,sin??,Q?3?sin?,?1?cos??,(?是参数),则|PQ|的最大值与最小值的和为 .
2 答案 1.[巩固1] D,[巩固2]y=4x (x>0),[迁移]在平面ABCD上建立平面直角坐标系,选C。
2、[巩固1] (x-1)2+(y+1)2= 5,[巩固2]∵点M在第一象限,∴过点M与两坐标轴相切的圆的方程可设为:(x-r)2+(y-r)2= r2 , ∵圆过M(x0,y0)点,∴(x0-r)2+(y0-r)2= r2,整理得: r2-2(x0+y0)r+ x02+y02=0,由题意知r1,r2为该方程的两根,故r1r2= x02+y02。[迁移]在曲线C
上任取一点M(x0,y0),x04+y02=1, ∵|x0|≤1, ∴x04≤x02, ∴x02+y02 ≥x04+y02=1,即点M在圆 x2+y2=1外,选①②③⑥;3、[巩固1]D,[巩固2]-1,[迁移]A;4、[巩固1]A,[巩固2] 圆x2+y2+2x+2y-3=0的圆心A(-1,-1),半径为5,⊙M始终平分⊙A的周长即
两圆的公共弦是⊙A的直径,A在直线:2(a+1)+2(b+1)y-(a2+b2)+3=0上,将a点坐标代入即得,选B;[迁移] y?4x(x?0)和y?0(x?0),5、[巩固1]1,[巩固2]易知⊿ABC为直角三角形,a=6,b=8,c=10,则内切圆半径r=2,以C为原点建系,设P(2cos?,2sin?), PA2+PB2+PC2=80-8sin?,最大值为88,[迁移] |PQ|的最大、最小值分别为?2,和为22,注:题中参数?是同一个,因此点P,Q是互相有关联的,不是分别在两上圆上的任意点.因此借助图形去直观地求解很容易出错。
