《数值分析》
实验报告册
姓名:
学号:
专业:
年级:
计算机科学学院
计算机应用教研室
20##年春季学期
目录
实验一................................................ 3
实验二................................................ 5
实验三................................................ 7
实验四............................................... 10
实验五............................................... 12
实验六............................................... 15
实验七……………………………………………………………………18
实验一
一、课题名称
非线性方程数值解法
二、目的和意义
学会常用的插值方法，求函数的近似表达式，以解决其它实际问题；明确插值多项式和分段插值多项式各自的优缺点；熟悉插值方法的程序编制；如果绘出插值函数的曲线，观察其光滑性。
三、计算公式
Lagrange插值公式：
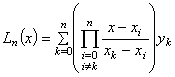
牛顿插值公式：
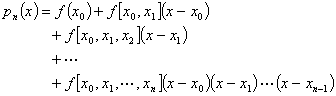
四、结构程序设计
程序设计:
#include"math.h"
float f(float x)
{
return((x*x*x-1)/3); /*牛顿迭代函数*/
}
main()
{
float x1,x2,eps,d;int k=0;
clrscr();
printf("\n input x1="); /*输入迭代初值*/
scanf("%f",&x1);
printf("\n input eps="); /*输入求解精度eps*/
scanf("%f",&eps);
do{
k++;
x1=x2;
x2=f(x1);
printf("\n %d %f\n",k,x2);
}while(fabs(x2-x1)＞=eps);
printf("the root of f(x)=0 is x=%f,k=%d\n",x2,k); /*输出x和迭代次数k*/
getch();
}
五、结果讨论和分析
计算结果分析：
将六种迭代格式分别代入程序试验：
（1）第一种格式：无论何值都无法求出，即发散
（2）第二种格式：初值为任意的x（x2＜=1），精度为0.00001
X=-0.347296，k=6
其他值为发散。
（3）第三种格式：初值为任意的x（x＞0），精度为0.0001
X=1.879372，k=10
其他值为发散。
（4）第四种格式：初值为任意值，精度为0.00001
X=-0.347296,k=5
（5）第五种格式：初值为任意值,精度为0.00001
X=-0.347296,k=4
（6）第六种格式：初值为任意值，精度为0.00001
X=-0.347296,k=4
由此可知不同的初值对公式的计算有影响，当初值不满足函数的收敛条件时，无法计算结果，函数发散。
精度的大小不同也使迭代函数迭代的次数不同，从而影响xn的近似程度。
实验二
一、课题名称
解线性方程组的直接方法
二、目的和意义
掌握线性方程组直接接法的基本思想；了解不同数值方法解线性方程组的原理、实现条件、使用范围、计算公式；培养编程与上机调试能力。
三、计算公式
消去法
四、结构程序设计
用追赶法求解线性方程组
#include"stdio.h"
main()
{
FILE*f;
double a[15],b[15],c[15],d[15];
double t;
int i,n;
f=fopen("zgf.dat","r");
fscanf(f,"%d",&n);
fscanf(f,"%lf%lf%lf",&b[1],&c[1],&d[1]);
for(i=2;i＜=n-1;i++)
{
fscanf(f,"%lf%lf%lf%lf",&a[i],&b[i],&c[i],&d[i]);
}
fscanf(f,"%lf%lf%lf",&a[n],&b[n],&d[n]);
fclose(f);
c[1]=c[1]/b[1];
d[1]=d[1]/b[1];
for(i=2;i＜=n-1;i++)
{
t=b[i]-c[i-1]*a[i];
c[i]=c[i]/t;
d[i]=(d[i]-d[i-1]*a[i])/t;
}
d[n]=(d[n]-d[n-1]*a[n])/(b[n]-c[n-1]*a[n]);
for(i==n-1;i＞=1;i--)d[i]=d[i]-c[i]*d[i+1];
printf("\n***************\n");
for(i=1;i＜=n;i++)
printf("d[%2d]=%lf\n",i,d[i]);
}
五、结果讨论和分析
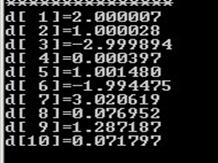
此方法通过有限步算术运算求出精确解，但实际计算由于舍入误差的影响，只能求出近似解。
实验三
一、课题名称
解线性方程组的迭代法
二、目的和意义
了解各迭代法的基本原理和特点，判断雅克比迭代、高斯-塞德尔迭代对任意初始向量的收敛性，完成雅克比迭代、高斯-塞德尔迭代算法的程序实现
三、计算公式
l 雅可比
xi(k+1)=1/aii(bi-Σaijxj(k))
l 高斯-塞德尔
xi(k+1)=1/aii(bi-Σaijxj(k+1)-Σaijxj(k))
l 超松弛迭代
xi(k+1)=（1-w）xi(k)+w*(bi-Σaijxj(k+1)-Σaijxj(k)) /aii
四、结构程序设计
高斯-塞德尔法：
#include"math.h"
#define M 8
#define N 9
main()
{
double a[M][N]={{4,2,-4,0,2,4,0,0,0},
{2,2,-1,-2,1,3,2,0,-6},
{-4,-1,14,1,-8,-3,5,6,20},
{0,-2,1,6,-1,-4,-3,3,23},
{2,1,-8,-1,22,4,-10,-3,9},
{4,3,-3,-4,4,11,1,-4,-22},
{0,2,5,-3,-10,1,14,2,-15},
{0,0,6,3,-3,-4,2,19,45}};
double x[M]={0,0,0,0,0,0,0,0};
double r,t,q,eps=0.0001;
int k,i,j,T=100;
for(i=0;i
{
for(j=0;j
printf("%1f",a[i][j]);
printf("\n");
}
for(k=0;k
{
r=0;
for(i=0;i
{
t=x[i];
q=0;
for(j=0;j
if(j!=i)q=q+a[i][j]*x[j];
x[i]=(a[i][N-1]-q)/a[i][i];
if(fabs(x[i]-t)＞r)r=fabs(x[i]-t);
}
if(r
printf("\nk=%d,",k);
for(i=0;i
printf("\nx[%d]=%lf",i,x[i]);
}
if(k==T)printf("\nNo");
else
for(i=0;i
printf("x(%d)=%15.7f\n",i+1,x[i]);
}
五、结果讨论和分析
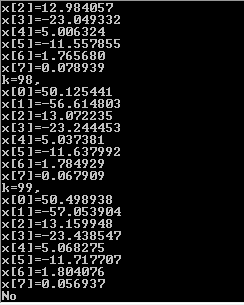
与直接法相比，迭代法适用于稀疏矩阵的线性方程组
实验四
一、课题名称
函数插值方法
二、目的和意义
了解多项式差值公式的存在唯一性条件及其余项表达式的推导，了解拉格朗日插值多项式的构造、计算及其基函数的特点，牛顿插值多项式的构造与应用，差商、差分的计算及基本性质。
三、计算公式
=
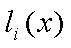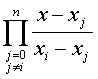，i=0,1,2…n
P(X)=p(x)+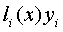
(p(x)的初值是0)。
四、结构程序设计
#include"stdio.h"
#include"math.h"
#include"string.h"
#include"conio.h"
#include"stdlib.h"
#define n 5
double x1[]={0.4,0.55,0.65,0.80,0.95,1.05};
double y1[]={0.41075,0.57815,0.69675,0.90,1.00,1.25382};
main()
{
double Lag(double x1[],double y1[],float t);
int m,k;float x,y;float X;double z;
printf("\nthe number of the interpolation points is m:");
scanf("%d",&m);
for(k=1;k＜=m;k++)
{
printf("\ninputX%d=",k);
scanf("%f",&X);
z=Lag(x1,y1,X);
printf("P(%f)=%f\n",X,z);
}
getch();
return(0);
}
double Lag(double x[],double y[],float X)
{
int i,j;
double L,P;
P=0.0;
for(i=0;i＜=n;i++)
{
L=1.0;
for(j=0;j＜=n;j++)
if(j!=i)
L=L*(X-x[j])/(x[i]-x[j]);
P=P+y[i]*L;
}
return (P);
}
五、结果讨论和分析
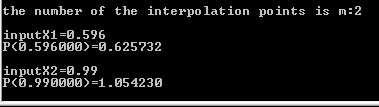
实验五
一、课题名称
曲线拟合的最小二乘法
二、的和意义
掌握曲线拟合的最小二乘法；了解最小二乘法亦可以用于解超定线性方程组；探索拟合函数的选择与拟合精度间的关系。
三、计算公式
e 22=Σε2i=Σ[φ(xi)-f(xi)]2
四、结构程序设计
#include "stdio.h"
#include "math.h"
#define num 10
float neiji(float b[num],float c[num])
{ int p;
float nj=0;
for(p=1;p
nj+=c[p]*b[p];
return nj;
}
float s[num],x[num],fai[num][num],afa[num];
float beida[num],a[num],xfai[num],yd[num],max,pcpfh;
void main()
{ int i,j,k,n,index,flag;
char conti;
conti=' ';
printf("请输入已知点的个数n=\n");
scanf("%d",&n);
printf("请输入x和y:");
for(i=1;i＜=n;i++)
{ printf("x[%d]=",i);
scanf("%f",&x[i]);
printf("y[%d]=",i);
scanf("%f","&y[i]");
}
while(conti==' ')
{ printf("请输入拟和次数=");
scanf("%d",&index);
pcpfh=0;
afa[1]=0;
a[0]=0;
for(i=1;i＜=n;i++)
{ afa[1]+=x[i];
a[0]+=yd[i];
fai[0][i]=1;
}
afa[1]=afa[1]/n;
a[0]=a[0]/n;
for(i=1;i＜=n;i++)
{
fai[1][i]=x[i]-afa[1];
}
a[1]=neiji(fai[1],yd)/neiji(fai[1],fai[1]);
for(k=1;k
{ for(i=1;i＜=n;i++)
xfai[i]=x[i]*fai[k][i];
afa[k+1]=neiji(fai[k],xfai)/neiji(fai[k],fai[k]);
beida[k]=neiji(fai[k],fai[k])/neiji(fai[k-1],fai[k-1]);
for(j=1;j＜=n;j++)
fai[k+1][j]=(x[j]-afa[k+1])*fai[k][j]-beida[k]*fai[k-1][j];
a[k+1]=neiji(fai[k+1],yd)/neiji(fai[k+1],fai[k+1]);
}
printf("%d次拟和结果为\n",index);
for(i=0;i＜=index;i++)
printf("a[%d]=%f\n",i,a[i]);
for(i=1;i＜=index;i++)
printf("afa[%d]=%f\n",i,afa[i]);
for(i=1;i
printf("beida[%d]=%f\n",i,beida[i]);
for(i=1;i＜=n;i++)
{ for(k=0;k＜=index;k++)
s[i]+=a[k]*fai[k][i];
yd[i]=fabs(yd[i]-s[i]);
pcpfh+=yd[i]*yd[i];
s[i]=0;
}
max=0;
for(i=1;i＜=n;i++)
if(yd[i]＞max)
{max=yd[i];
flag=i;
}
printf("当x=%f时,偏差最大=%f,偏差平方和为%f\n",x[flag],max,pcpfh);
printf("继续拟和请按space,按其他键退出");
conti=getchar();
conti=getchar();
}
}
五、结果讨论和分析
请输入已知点的个数n=10
请输入x和y：
x[1]=0
y[1]=0
……
请输入拟合次数=5
5次拟合结果为
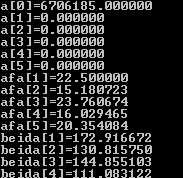
当x=0.000000时，偏差最大=6706185.000000，偏差平方和为449729146126336.000000.
实验六
一、课题名称
数值积分与数值微分
二、目的和意义
深刻认识数值积分法的意义；明确数值积分精度与步长的关系；根据定积分的计算方法，可以考虑二重积分的计算问题。
三、计算公式
Ｓｎ=1/6*[f(a)+4Σf(xk+1/2)+2Σf(xk)+f(b)]
Rn=64/63*c2n-1/63*cn
四、结构程序设计
Romberg算法:
#include"stdio.h"
#include"math.h"
#include"conio.h"
float f(float x)
{return(exp(x)/(4+x*x));}
main()
{
float a=0,b=1;
float h=b-a,T1,T2,s,x;
int i;T1=h/2*(f(a)+f(b));
for(i=0;i＜3;i++)
{
printf("h=%f,T=%f\n",h,T1);
s=0;
x=a+h/2;
while(x
{
s+=f(x);
x+=h;
}
T2=T1/2+h/2*s;
h/=2;T1=T2;
}
printf("h=%f,T=%f\n",h,T1);
return;
}
Simpson算法：
#include"stdio.h"
#include"math.h"
#include"conio.h"
#define Max_M 20
float f(float x)
{return(sin(x)/x);}
float Simpson(float a,float b,int n)
{
int k;float x,s1,s2,h=(b-a)/n;
x=a+h/2;
s1=f(x);s2=0;
for(k=1;k
{
s1=s1+f(a+k*h+h/a);
s2=s2+f(a+k*h);
}
s2=h*(f(a)+4*s1+2*s2+f(b))/6;
return(s2);
}
main()
{
int i,n;float a1,b1,s=0;
printf("\n Input the begin:");
scanf("%f",&a1);
printf("\n Input the end:");
scanf("%f",&b1);
do {
printf("\n input n divde value[divide(%f,%f)]:",a1,b1);
scanf("%d",&b1);
}
while(n＜=1&&n＞Max_M);
s=Simpson(a1,b1,n);
printf("solve is:%f",s);
getch();
return(s);
}
五、结果讨论和分析
用Romberg法得出结果为：
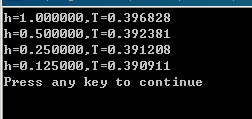
用Simpson法得出结果为：
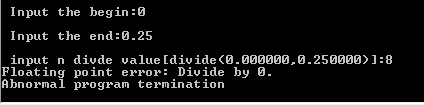
可见复化公式要先估计出步长，步长的大小将影响计算结果和精度
实验七
一、课题名称
常微分方程的数值解法
二、目的和意义
熟悉各种初值的问题的算法，编出算法程序；
明确各种算法的精度寓所选步长有密切关系；
通过计算更加了解各种算法的优越性；
三、计算公式
k1=f(xi,yi)
k2=f(xi+1/2+1/2,yi+h/2*k1)
k3=f(xi+1/2,yi+h/2*k2)
k4=f(xi+1,yi+h*k3)
Yi+1=yi+h*(k1,2*k2+2*k3+k4)/6
四、结构程序设计
Rung-kutta法：
#include"math.h"
#include"string.h"
#include"stdio.h"
#include"conio.h"
float f(float x,float y)
{
float y1;
y1=y-2*x/y;
return y1;
}
float Runge_Kutta(float x,float y,float h)
{
float k1,k2,k3,k4;
k1=f(x,y);k2=f(x+h/2,y+h*k1/2);
k3=f(x+h/2,y+h*k2/2);k4=f(x+h,y+h*k3);
return(y+h*(k1+2*k2+2*k3+k4)/6);
}
main()
{
int i=0;
float x,y,h,b;
clrscr();
printf("\n Input begin x0:");
scanf("%f",&x);
printf("\n Input begin y0:");
scanf("%f",&y);
printf("\n Input step h:");
scanf("%f",&h);
printf("\n Input end b:");
scanf("%f",&b);
printf("\n x0=%10f y0=%10f\n",x,y);
do
{
y=Runge_Kutta(x,y,h);
x=x+h;i++;
printf("x%d=%10f y%d=%10f\n",i,x,i,y);
}
while(x
getch();
return(y);
}
五、结果讨论和分析
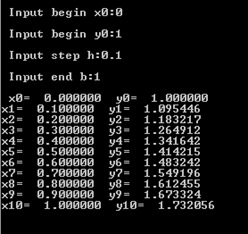
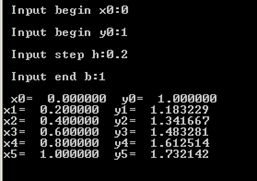
可见步长的选取会影响节点处数值解的误差