重 庆 交 通 大 学
学 生 实 验 报 告
实验课程名称 计 算 方 法 开课实验室 数学实验室 学 院 2011 年级 专业班
学 生 姓 名 学 号
开 课 时 间 2013 至 2014 学年 第 1 学期
目 录
实验一 xxxxx............................................................................ 1
实验二 xxxxx............................................................................ 3 实验三
实验四
xxxxxxx ....................................................................... 5 xxxxx............................................................................ 3
计算方法实验报告
实验一 列主元消去法
一、 实验目的:
1.认识并了解列主元消去法的相关知识及原理。
2.学习并使用列主元法解线性方程组。
二、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境。
三、实验内容及要求:
实验内容:用列主元消去法求解某个方程组。
考虑一:所解线性方程组为病态方程还是良态方程组。
四、实验步骤与结果分析
(一) 实验源程序
function x=liezhuyuan(A,b)
n=length(b);
x=zeros(n,1);
c=zeros(1,n);
t=0;
for i=1:n-1
max=abs(A(i,i));
m=i;
for j=i+1:n
if max<abs(A(j,i))
max=abs(A(j,i));
m=j;
end
end
if m~=i
for k=1:n
c(k)=A(i,k);
A(i,k)=A(m,k);
A(m,k)=c(k);
end
t=b(i);
b(i)=b(m);
b(m)=t;
end
for k=i+1:n
for j=i+1:n
A(k,j)=A(k,j)-A(i,j)*A(k,i)/A(i,i);
end
第1页
计算方法实验报告
b(k)=b(k)-b(i)*A(k,i)/A(i,i);
A(k,i)=0;
end
end
x(n)=b(n)/A(n,n);
for i=n-1:-1:1
sum=0;
for j=i+1:n
sum=sum+A(i,j)*x(j);
end
x(i)=(b(i)-sum)/A(i,i);
end
(二) 实验结果分析
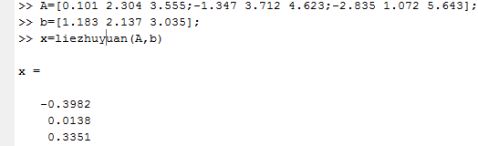
实验分析:在实验中,经过代码的多次调试与修改,终于得到了实验结果。但是,透过实验结果,我们看到实验结果的字长有限,导致实验与精确值之间存在误差,在以后的实验的实验中要想办法减小误差,提高解的精读。故,可以通过采用双倍字长进行运算来改善解的精读。同时,当方程组矩阵元素的数量级相差悬殊时,用列主元消去法会导致有效数字严重损失,可以先用系数矩阵每行元素的最大模除遍行或列各元素,然后施行列主元消去法。
第2页
计算方法实验报告
实验二 高斯-赛德尔迭代法
一、实验目的
1.了解并理解赛德尔迭代法及迭代法的收敛性。
2.学习并应用高斯-赛德尔迭代法求解线性方程。
二、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境。
三、实验内容及要求:
实验内容:用高斯-塞德尔迭代法求解某个线性方程组。 实验要求:考虑迭代的收敛速度及收敛性。
四、实验步骤与结果分析
(一) 实验源程序
function [x,k]=Gaussseidel(A,b,x0,emg,N)
if nargin<5
N=500;
else
N=N;
end
n=length(b);
x1=zeros(n,1);
x2=zeros(n,1);
x1=x0;
r=max(abs(b-A*x1));
k=0;
while(r>emg)&(k<N)
for i=1:n
sum=0;
for j=1:n
if j>i
sum=sum+A(i,j)*x1(j);
elseif j<i
sum=sum+A(i,j)*x1(j);
end
end
x2(i)=(b(i)-sum)/A(i,i);
end
r=max(abs(x2-x1));
第3页
计算方法实验报告
x1=x2;
k=k+1;
if k>N
wangring('迭代次数达到上限!');
return;
end
end
x=x1;
(三) 实验结果分析
结果分析:根据实验结果,经过40次的迭代计算得到了方程组的近似解。因为方程组的解的字长较短,使实验结果存在误差。在实验中,有些误差是不可以避免,而有些误差则可以通过改进方法等方式来改善。在本实验中,可以通过增加字长来减少误差。同时,也可以发现迭代次数较多。虽然迭代法的收敛与初始向量无关,但是它对于迭代次数却有很大影响,所以也要重视初始向量的选取。

第4页
计算方法实验报告
实验三 牛顿迭代法求方程的近似根
一、实验目的
1.了解牛顿迭代法的基本思想及相关知识。
2.学习并应用牛顿迭代求解非线性方程组的近似根的方法。
二、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境验环境。
三、实验内容:
用牛顿迭代法求某个非线性方程组的近似根。
四、算法描述:
五、实验结果与分析
(一) 实验源程序
f=input('输入函数:f(x)=');
n=input('请输入迭代次数:n=');
x0=input('请输入迭代初始值:x0=');
f1=diff(f);
for i=1:n
x=x0;
fx0=eval(f);
f1x0=(f1);
x0=x0-fx0/f1x0;
end
(二) 实验结果

第5页
计算方法实验报告
(二) 实验结果分析
对于非线性方程f(x)=0的根求解,可以使用牛顿迭代法、二分法或者弦线法等.在本 试验中使用牛顿迭代法进行求解非线性方程,根据试验结果,经过6次迭代之后得到 方程的近似解.但是将其代入方程时,发现其存在较大的误差.因此,在使用牛顿迭代 求解非线性方程时,可以通过增加迭代次数或者使用牛顿迭代法的修正形式(重根情 形)减小试验误差.科学的美丽有时在于我们可以通过实验而获得充实感吧.
第6页
计算方法实验报告
实验四 拉格朗日插值法
一、实验目的
1.了解拉格朗日插值的含义及其相关性质。
2.学习并使用拉格朗日插值法求解函数的一些点。.
二、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境。
三、实验内容:
用拉格朗日插值法求解某个函数表对应函数的一些点。.
四、算法描述:
五、实验结果与分析
(一) 实验源程序
function yy=Lagrange(x,y,xi)
m=length(x);n=length(y);
if m~=n,error('向量x与向量y的长度必须一致');end s=0;
for i=1:n
z=ones(1,length(xi));
for j=1:n
if j~=i
z=z.*(xi-x(j))/(x(i)-x(j));
end
end
s=s+z*y(i);
end
yy=s;
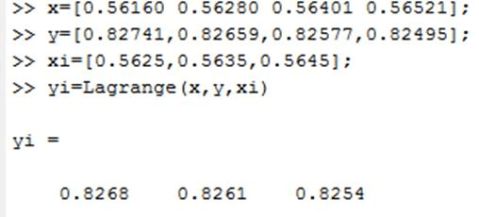
(二) 实验结果
第1页
计算方法实验报告
(二) 实验结果分析
在实际问题中经常遇到这种情况:可以断定所考虑函数在某个区间上存在且连续,但是却难以找到它的解析表达式,只能得到它在某些点处的函数(即一张函数表)。这时,可以通过插值法来分析函数性态或者直接求出其他一些点的函数值。根据实验结果,使用龙贝格插值法可以由一个函数表,求解出了其他某一些点。因此,可以广泛的应用插值法于生产实际与科学研究。
第2页
计算方法实验报告
实验五 龙贝格积分法
一、实验目的和意义
1.认识并了解龙贝格积分法.
2.学习并使用龙贝格积分法求解积分近似值。
二、实验内容
用龙贝格积分法求解某个定积分近似值。
三、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境。
四、实验要求:
五、实验源程序
function [s,n]=rombergl(a,b,epsl)
f=inline('4/(1+x^2)');
a=0;
b=1;
esp1=5e-6;
s=10;
s0=0;
k=2;
t=[];
t(1,1)=(b-a)*(f(b)+f(a))/2;
while abs(s-s0)>esp1
h=(b-a)/2^(k-1);
w=0;
if h~=0
for i=1:2^(k-1)-1
w=w+f(a+i*h);
end
t(k,1)=h*(f(a)/2+w+f(b)/2);
for l=2:k
for i=1:(k-l+1)
t(i,l)=(4^(l-1)*t(i+1,l-1)-t(i,l-1))/(4^(l-1)-1);
end
end
s=t(1,k);
第3页
计算方法实验报告
s0=t(1,k-1);
k=k+1;
n=k;
else
s0=s;
n=-k;
end
end
s
n
六、结果分析
由实验结果,使用龙贝格积分法快速成功的求解了某个定积分的近似值。虽然龙贝格算法规律较强,不需要存贮求积系数,占用存贮单元少,精度较高,但是每加速一次就要计算新分点的函数值,所以计算量较大。综合来看,龙贝格算法是计算定积分数值解的一种十分有效的方法,可以将其应用于积分或微分数值解相关的实际问题

第4页
计算方法实验报告
实验六 改进的欧拉法
一、实验目的和意义
1.了解欧拉公式及相关知识。
2.学习并使用改进的欧拉法求解常微分方程的数值解。
二、实验内容
用改进的欧拉法求解常微分方程的数值解并画出函数图像。
三、实验设备和实验环境
实验设备:笔记本电脑acer t3820。
实验环境:window7旗舰版电脑系统下matlab 2011b软件环境。
四、实验要求:
xxxxx。
xxxx。
五、实验源程序
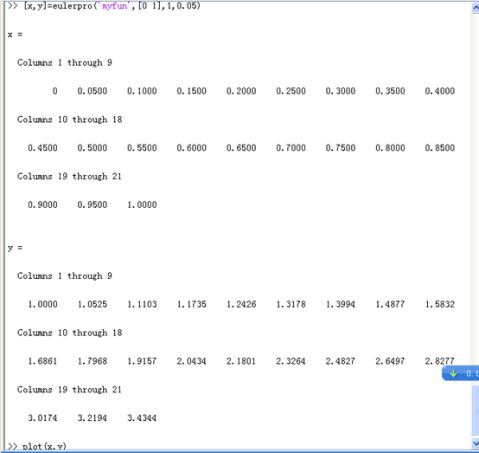
function [xout,yout]=eulerpro(ypfun,xspan,y0,h)
f=ypfun;
x=xspan(1):h:xspan(2);
n=length(x);
y=zeros(1,n);
y(1)=y0;
for i=1:n-1
yp=y(i)+h*feval(f,x(i),y(i));
yc=y(i)+h*feval(f,x(i+1),yp);
y(i+1)=(yp+yc)/2;
end
xout=x;
yout=y;
function f=myfun(x,y)
f=x+y;
第1页
计算方法实验报告
六、结果分析
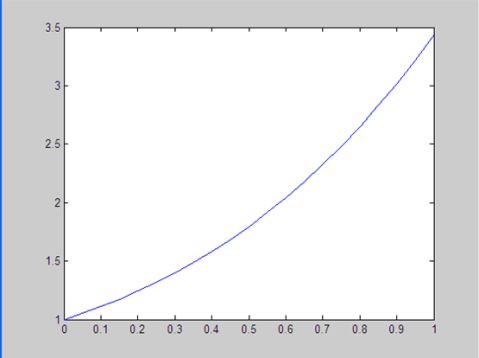
在实际中,很多问题的数学模型都是微分方程。常微分方程作为微分方程的基本类型之一,可以通过单步法或改进的欧拉法来进行求解。在实验中,使用改进的欧拉法求解出常微分方程中一些点,并画出了常微分方程的图像。在自然与工程界某些问题的数学表述都可以归结为常微分方程的定解问题,故可以将改进的欧拉法应用于自然与工程中的实际问题中。
第2页
第二篇:数值分析实验报告(1)
《数值分析》
实验报告册
姓名:
学号:
专业:
年级:

计算机科学学院
计算机应用教研室
2008年春季学期
目录
实验一................................................ 3
实验二................................................ 5
实验三................................................ 7
实验四............................................... 10
实验五............................................... 12
实验六............................................... 15
实验七……………………………………………………………………18
实验一
一、课题名称
非线性方程数值解法
二、目的和意义
学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;明确插值多项式和分段插值多项式各自的优缺点;熟悉插值方法的程序编制;如果绘出插值函数的曲线,观察其光滑性。
三、计算公式
Lagrange插值公式:

牛顿插值公式:
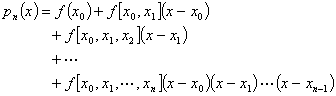
四、结构程序设计
程序设计:
#include"math.h"
float f(float x)
{
return((x*x*x-1)/3); /*牛顿迭代函数*/
}
main()
{
float x1,x2,eps,d;int k=0;
clrscr();
printf("\n input x1="); /*输入迭代初值*/
scanf("%f",&x1);
printf("\n input eps="); /*输入求解精度eps*/
scanf("%f",&eps);
do{
k++;
x1=x2;
x2=f(x1);
printf("\n %d %f\n",k,x2);
}while(fabs(x2-x1)>=eps);
printf("the root of f(x)=0 is x=%f,k=%d\n",x2,k); /*输出x和迭代次数k*/
getch();
}
五、结果讨论和分析
计算结果分析:
将六种迭代格式分别代入程序试验:
(1)第一种格式:无论何值都无法求出,即发散
(2)第二种格式:初值为任意的x(x2<=1),精度为0.00001
X=-0.347296,k=6
其他值为发散。
(3)第三种格式:初值为任意的x(x>0),精度为0.0001
X=1.879372,k=10
其他值为发散。
(4)第四种格式:初值为任意值,精度为0.00001
X=-0.347296,k=5
(5)第五种格式:初值为任意值,精度为0.00001
X=-0.347296,k=4
(6)第六种格式:初值为任意值,精度为0.00001
X=-0.347296,k=4
由此可知不同的初值对公式的计算有影响,当初值不满足函数的收敛条件时,无法计算结果,函数发散。
精度的大小不同也使迭代函数迭代的次数不同,从而影响xn的近似程度。
实验二
一、课题名称
解线性方程组的直接方法
二、目的和意义
掌握线性方程组直接接法的基本思想;了解不同数值方法解线性方程组的原理、实现条件、使用范围、计算公式;培养编程与上机调试能力。
三、计算公式
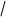 消去法
消去法
设a(k)kk=0,对k=1,2,……,n-1计算
 mik=a(k)ik/a(k)kk
mik=a(k)ik/a(k)kk
a(k+1)ij=a(k)ij-mika(k)kj i,j=k+1,k+2,……,n
b(k+1)i=b(k)i-mikb(k)k

 x
n=b
(n)
n/a
(n)
nn
x
n=b
(n)
n/a
(n)
nn
 x
i=(b
(i)
i-Σa
(i)
ijx
j)/a
(i)
ii i=n-1,n-2,……,1
x
i=(b
(i)
i-Σa
(i)
ijx
j)/a
(i)
ii i=n-1,n-2,……,1
平方根法 追赶法
lij=(aii-Σl2ik)1/2 Ly=f
lji=(aji-Σljklik)/lii j=i+1,i+2,……,n Ux=y
y1=f1/l1
y2=(fi-aiyi-1)/li i=2,3,……,n
四、结构程序设计
用追赶法求解线性方程组
#include"stdio.h"
main()
{
FILE*f;
double a[15],b[15],c[15],d[15];
double t;
int i,n;
f=fopen("zgf.dat","r");
fscanf(f,"%d",&n);
fscanf(f,"%lf%lf%lf",&b[1],&c[1],&d[1]);
for(i=2;i<=n-1;i++)
{
fscanf(f,"%lf%lf%lf%lf",&a[i],&b[i],&c[i],&d[i]);
}
fscanf(f,"%lf%lf%lf",&a[n],&b[n],&d[n]);
fclose(f);
c[1]=c[1]/b[1];
d[1]=d[1]/b[1];
for(i=2;i<=n-1;i++)
{
t=b[i]-c[i-1]*a[i];
c[i]=c[i]/t;
d[i]=(d[i]-d[i-1]*a[i])/t;
}
d[n]=(d[n]-d[n-1]*a[n])/(b[n]-c[n-1]*a[n]);
for(i==n-1;i>=1;i--)d[i]=d[i]-c[i]*d[i+1];
printf("\n***************\n");
for(i=1;i<=n;i++)
printf("d[%2d]=%lf\n",i,d[i]);
}
五、结果讨论和分析

此方法通过有限步算术运算求出 精确解,但实际计算由于舍入误差的影响,只能求出近似解。
实验三
一、课题名称
解线性方程组的迭代法
二、目的和意义
了解各迭代法的基本原理和特点,判断雅克比迭代、高斯-塞德尔迭代对任意初始向量的收敛性,完成雅克比迭代、高斯-塞德尔迭代算法的程序实现
三、计算公式
l 雅可比
xi(k+1)=1/aii(bi-Σaijxj(k))
l 高斯-塞德尔
xi(k+1)=1/aii(bi-Σaijxj(k+1)-Σaijxj(k))
l 超松弛迭代
xi(k+1)=(1-w)xi(k)+w*(bi-Σaijxj(k+1)-Σaijxj(k)) /aii
四、结构程序设计
高斯-塞德尔法:
#include"math.h"
#define M 8
#define N 9
main()
{
double a[M][N]={{4,2,-4,0,2,4,0,0,0},
{2,2,-1,-2,1,3,2,0,-6},
{-4,-1,14,1,-8,-3,5,6,20},
{0,-2,1,6,-1,-4,-3,3,23},
{2,1,-8,-1,22,4,-10,-3,9},
{4,3,-3,-4,4,11,1,-4,-22},
{0,2,5,-3,-10,1,14,2,-15},
{0,0,6,3,-3,-4,2,19,45}};
double x[M]={0,0,0,0,0,0,0,0};
double r,t,q,eps=0.0001;
int k,i,j,T=100;
for(i=0;i<M;i++)
{
for(j=0;j<N;j++)
printf("%1f",a[i][j]);
printf("\n");
}
for(k=0;k<T;k++)
{
r=0;
for(i=0;i<M;i++)
{
t=x[i];
q=0;
for(j=0;j<M;j++)
if(j!=i)q=q+a[i][j]*x[j];
x[i]=(a[i][N-1]-q)/a[i][i];
if(fabs(x[i]-t)>r)r=fabs(x[i]-t);
}
if(r<eps)break;
printf("\nk=%d,",k);
for(i=0;i<M;i++)
printf("\nx[%d]=%lf",i,x[i]);
}
if(k==T)printf("\nNo");
else
for(i=0;i<M;i++)
printf("x(%d)=%15.7f\n",i+1,x[i]);
}
五、结果讨论和分析

与直接法相比,迭代法适用于稀疏矩阵的线性方程组
实验四
一、课题名称
函数插值方法
二、目的和意义
了解多项式差值公式的存在唯一性条件及其余项表达式的推导,了解拉格朗日插值多项式的构造、计算及其基函数的特点,牛顿插值多项式的构造与应用,差商、差分的计算及基本性质。
三、计算公式
 =
= ,i=0,1,2…n
,i=0,1,2…n
P(X)=p(x)+ (p(x)的初值是0)。
(p(x)的初值是0)。
四、结构程序设计
#include"stdio.h"
#include"math.h"
#include"string.h"
#include"conio.h"
#include"stdlib.h"
#define n 5
double x1[]={0.4,0.55,0.65,0.80,0.95,1.05};
double y1[]={0.41075,0.57815,0.69675,0.90,1.00,1.25382};
main()
{
double Lag(double x1[],double y1[],float t);
int m,k;float x,y;float X;double z;
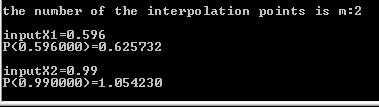
printf("\nthe number of the interpolation points is m:");
scanf("%d",&m);
for(k=1;k<=m;k++)
{
printf("\ninputX%d=",k);
scanf("%f",&X);
z=Lag(x1,y1,X);
printf("P(%f)=%f\n",X,z);
}
getch();
return(0);
}
double Lag(double x[],double y[],float X)
{
int i,j;
double L,P;
P=0.0;
for(i=0;i<=n;i++)
{
L=1.0;
for(j=0;j<=n;j++)
if(j!=i)
L=L*(X-x[j])/(x[i]-x[j]);
P=P+y[i]*L;
}
return (P);
}
五、结果讨论和分析
实验五
一、课题名称
曲线拟合的最小二乘法
二、的和意义
掌握曲线拟合的最小二乘法;了解最小二乘法亦可以用于解超定线性方程组;探索拟合函数的选择与拟合精度间的关系。
三、计算公式



 e 22=Σε2i=Σ[φ(xi)-f(xi)]2
e 22=Σε2i=Σ[φ(xi)-f(xi)]2
四、结构程序设计
#include "stdio.h"
#include "math.h"
#define num 10
float neiji(float b[num],float c[num])
{ int p;
float nj=0;
for(p=1;p<num;p++)
nj+=c[p]*b[p];
return nj;
}
float s[num],x[num],fai[num][num],afa[num];
float beida[num],a[num],xfai[num],yd[num],max,pcpfh;
void main()
{ int i,j,k,n,index,flag;
char conti;
conti=' ';
printf("请输入已知点的个数n=\n");
scanf("%d",&n);
printf("请输入x和y:");
for(i=1;i<=n;i++)
{ printf("x[%d]=",i);
scanf("%f",&x[i]);
printf("y[%d]=",i);
scanf("%f","&y[i]");
}
while(conti==' ')
{ printf("请输入拟和次数=");
scanf("%d",&index);
pcpfh=0;
afa[1]=0;
a[0]=0;
for(i=1;i<=n;i++)
{ afa[1]+=x[i];
a[0]+=yd[i];
fai[0][i]=1;
}
afa[1]=afa[1]/n;
a[0]=a[0]/n;
for(i=1;i<=n;i++)
{
fai[1][i]=x[i]-afa[1];
}
a[1]=neiji(fai[1],yd)/neiji(fai[1],fai[1]);
for(k=1;k<index;k++)
{ for(i=1;i<=n;i++)
xfai[i]=x[i]*fai[k][i];
afa[k+1]=neiji(fai[k],xfai)/neiji(fai[k],fai[k]);
beida[k]=neiji(fai[k],fai[k])/neiji(fai[k-1],fai[k-1]);
for(j=1;j<=n;j++)
fai[k+1][j]=(x[j]-afa[k+1])*fai[k][j]-beida[k]*fai[k-1][j];
a[k+1]=neiji(fai[k+1],yd)/neiji(fai[k+1],fai[k+1]);
}
printf("%d次拟和结果为\n",index);
for(i=0;i<=index;i++)
printf("a[%d]=%f\n",i,a[i]);
for(i=1;i<=index;i++)
printf("afa[%d]=%f\n",i,afa[i]);
for(i=1;i<index;i++)
printf("beida[%d]=%f\n",i,beida[i]);
for(i=1;i<=n;i++)
{ for(k=0;k<=index;k++)
s[i]+=a[k]*fai[k][i];
yd[i]=fabs(yd[i]-s[i]);
pcpfh+=yd[i]*yd[i];
s[i]=0;
}
max=0;
for(i=1;i<=n;i++)
if(yd[i]>max)
{max=yd[i];
flag=i;
}
printf("当x=%f时,偏差最大=%f,偏差平方和为%f\n",x[flag],max,pcpfh);
printf("继续拟和请按space,按其他键退出");
conti=getchar();
conti=getchar();
}
}
五、结果讨论和分析
请输入已知点的个数n=10
请输入x和y:
x[1]=0
y[1]=0
……
请输入拟合次数=5
5次拟合结果为

当x=0.000000时,偏差最大=6706185.000000,偏差平方和为449729146126336.000000.
实验六
一、课题名称
数值积分与数值微分
二、目的和意义
深刻认识数值积分法的意义;明确数值积分精度与步长的关系;根据定积分的计算方法,可以考虑二重积分的计算问题。
三、计算公式
Sn=1/6*[f(a)+4Σf(xk+1/2)+2Σf(xk)+f(b)]
Rn=64/63*c2n-1/63*cn
四、结构程序设计
Romberg算法:
#include"stdio.h"
#include"math.h"
#include"conio.h"
float f(float x)
{return(exp(x)/(4+x*x));}
main()
{
float a=0,b=1;
float h=b-a,T1,T2,s,x;
int i;T1=h/2*(f(a)+f(b));
for(i=0;i<3;i++)
{
printf("h=%f,T=%f\n",h,T1);
s=0;
x=a+h/2;
while(x<b)
{
s+=f(x);
x+=h;
}
T2=T1/2+h/2*s;
h/=2;T1=T2;
}
printf("h=%f,T=%f\n",h,T1);
return;
}
Simpson算法:
#include"stdio.h"
#include"math.h"
#include"conio.h"
#define Max_M 20
float f(float x)
{return(sin(x)/x);}
float Simpson(float a,float b,int n)
{
int k;float x,s1,s2,h=(b-a)/n;
x=a+h/2;
s1=f(x);s2=0;
for(k=1;k<n;k++)
{
s1=s1+f(a+k*h+h/a);
s2=s2+f(a+k*h);
}
s2=h*(f(a)+4*s1+2*s2+f(b))/6;
return(s2);
}
main()
{
int i,n;float a1,b1,s=0;
printf("\n Input the begin:");
scanf("%f",&a1);
printf("\n Input the end:");
scanf("%f",&b1);
do {
printf("\n input n divde value[divide(%f,%f)]:",a1,b1);
scanf("%d",&b1);
}
while(n<=1&&n>Max_M);
s=Simpson(a1,b1,n);
printf("solve is:%f",s);
getch();
return(s);
}
五、结果讨论和分析
用Romberg法得出结果为:

用Simpson法得出结果为:

可见复化公式要先估计出步长,步长的大小将影响计算结果和精度
实验七
一、课题名称
常微分方程的数值解法
二、目的和意义
熟悉各种初值的问题的算法,编出算法程序;
明确各种算法的精度寓所选步长有密切关系;
通过计算更加了解各种算法的优越性;
三、计算公式
k1=f(xi,yi)
k2=f(xi+1/2+1/2,yi+h/2*k1)
k3=f(xi+1/2,yi+h/2*k2)
k4=f(xi+1,yi+h*k3)
Yi+1=yi+h*(k1,2*k2+2*k3+k4)/6
四、结构程序设计
Rung-kutta法:
#include"math.h"
#include"string.h"
#include"stdio.h"
#include"conio.h"
float f(float x,float y)
{
float y1;
y1=y-2*x/y;
return y1;
}
float Runge_Kutta(float x,float y,float h)
{
float k1,k2,k3,k4;
k1=f(x,y);k2=f(x+h/2,y+h*k1/2);
k3=f(x+h/2,y+h*k2/2);k4=f(x+h,y+h*k3);
return(y+h*(k1+2*k2+2*k3+k4)/6);
}
main()
{
int i=0;
float x,y,h,b;
clrscr();
printf("\n Input begin x0:");
scanf("%f",&x);
printf("\n Input begin y0:");
scanf("%f",&y);
printf("\n Input step h:");
scanf("%f",&h);
printf("\n Input end b:");
scanf("%f",&b);
printf("\n x0=%10f y0=%10f\n",x,y);
do
{
y=Runge_Kutta(x,y,h);
x=x+h;i++;
printf("x%d=%10f y%d=%10f\n",i,x,i,y);
}
while(x<b);
getch();
return(y);
}
五、结果讨论和分析

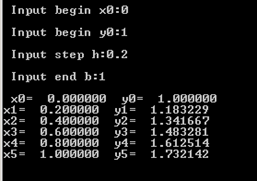
可见步长的选取会影响节点处数值解的误差
