考试重点
第一章:行列式的定义、行列式的计算;
第二章:1、求矩阵的逆阵(伴随矩阵法、初等变换法);
2、求矩阵的秩(用初等变换法);
3、求矩阵方程:Ax=B, xA=B, AxB=C;
第三章:证明向量组的线性相关性;
第四章:方程组Ax=0, Ax=b求解;
第五章:1、会求特征值与特征向量;
2、相似矩阵的性质;
3、实对称矩阵的对角化;
第六章:1、用正交变换把二次型化为标准形;
2、二次型的秩,二次型正定的定义;
3、矩阵正定的判断方法:
(1)各阶顺序主子式都大于零;(2)每个特征值都大于零



√ 行列式的计算:
① 若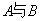 都是方阵(不必同阶),则
都是方阵(不必同阶),则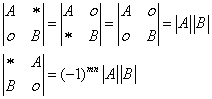
②上三角、下三角行列式等于主对角线上元素的乘积.
③关于副对角线: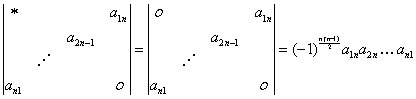
√ 逆矩阵的求法:
①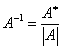
②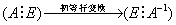
③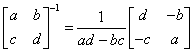
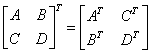
④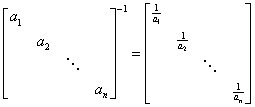

⑤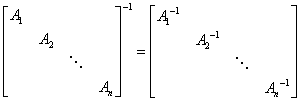

√ 设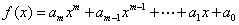 ,对
,对 阶矩阵
阶矩阵 规定:
规定: 为
为 的一个多项式.
的一个多项式.
√ 设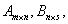
 的列向量为
的列向量为 ,
,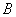 的列向量为
的列向量为 ,
,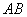 的列向量为
的列向量为 ,
,
√ 用对角矩阵 左乘一个矩阵,相当于用
左乘一个矩阵,相当于用 的对角线上的各元素依次乘此矩阵的行向量;
的对角线上的各元素依次乘此矩阵的行向量;
用对角矩阵 右乘一个矩阵,相当于用
右乘一个矩阵,相当于用 的对角线上的各元素依次乘此矩阵的列向量.
的对角线上的各元素依次乘此矩阵的列向量.
√ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘,
与分块对角阵相乘类似,即:

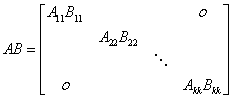
√ 判断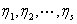 是
是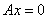 的基础解系的条件:
的基础解系的条件:
① 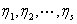 线性无关;
线性无关;
② 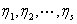 是
是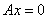 的解;
的解;
③  .
.
① 零向量是任何向量的线性组合,零向量与任何同维实向量正交.
② 单个零向量线性相关;单个非零向量线性无关.
③ 向量组 线性相关
线性相关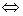 向量组中至少有一个向量可由其余
向量组中至少有一个向量可由其余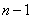 个向量线性表示.
个向量线性表示.
向量组 线性无关
线性无关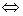 向量组中每一个向量
向量组中每一个向量 都不能由其余
都不能由其余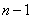 个向量线性表示.
个向量线性表示.
④ 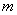 维列向量组
维列向量组 线性相关
线性相关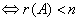 ;
;
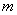 维列向量组
维列向量组 线性无关
线性无关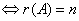 .
.
⑤ 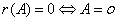 .
.
⑥ 若 线性无关,而
线性无关,而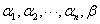 线性相关,则
线性相关,则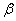 可由
可由 线性表示,且表示法惟一.
线性表示,且表示法惟一.
⑦ 矩阵的行向量组的秩等于列向量组的秩.
阶梯形矩阵的秩等于它的非零行的个数.
⑧ 矩阵的行初等变换不改变矩阵的秩,且不改变列 、行向量间的线性关系.
向量组等价  和
和 可以相互线性表示. 记作:
可以相互线性表示. 记作:
矩阵等价  经过有限次初等变换化为
经过有限次初等变换化为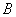 . 记作:
. 记作: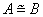
⑨ 矩阵 与
与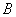 等价
等价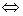
 作为向量组等价,即:秩相等的向量组不一定等价.
作为向量组等价,即:秩相等的向量组不一定等价.
矩阵 与
与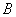 作为向量组等价
作为向量组等价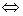
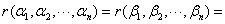
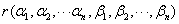
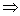
矩阵 与
与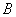 等价.
等价.
⑩ 向量组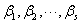 可由向量组
可由向量组 线性表示
线性表示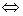
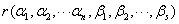
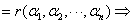
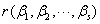 ≤
≤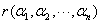 .
.
? 向量组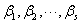 可由向量组
可由向量组 线性表示,且
线性表示,且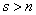 ,则
,则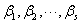 线性相关.
线性相关.
向量组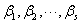 线性无关,且可由
线性无关,且可由 线性表示,则
线性表示,则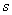 ≤
≤ .
.
? 向量组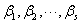 可由向量组
可由向量组 线性表示,且
线性表示,且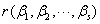
 ,则两向量组等价;
,则两向量组等价;
? 任一向量组和它的极大无关组等价.
? 向量组的任意两个极大无关组等价,且这两个组所含向量的个数相等.
? 若两个线性无关的向量组等价,则它们包含的向量个数相等.
? 若 是
是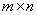 矩阵,则
矩阵,则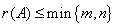 ,若
,若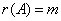 ,
, 的行向量线性无关;
的行向量线性无关;
若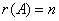 ,
, 的列向量线性无关,即:
的列向量线性无关,即:
 线性无关.
线性无关.
线性方程组的矩阵式  向量式
向量式 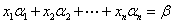
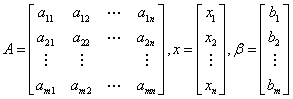
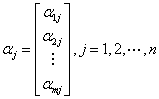
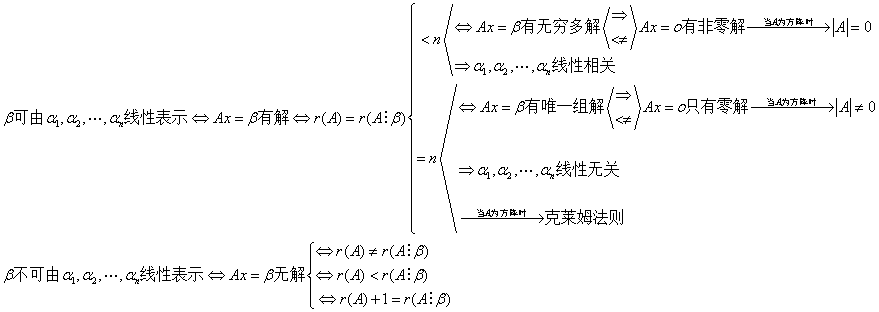

线性方程组解的性质:
√ 设 为
为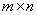 矩阵,若
矩阵,若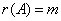 ,则
,则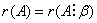 ,从而
,从而 一定有解.
一定有解.
当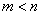 时,一定不是唯一解.
时,一定不是唯一解.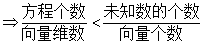 ,则该向量组线性相关.
,则该向量组线性相关.
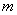 是
是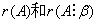 的上限.
的上限.
√ 矩阵的秩的性质:
① 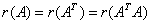
② 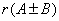 ≤
≤
③ 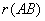 ≤
≤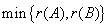
④ 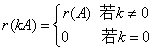
⑤ 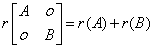
⑥ ≥
≥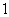
⑦ 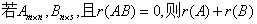 ≤
≤
⑧ 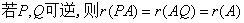
⑨ 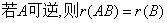
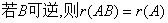
⑩ 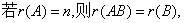 且
且 在矩阵乘法中有左消去律:
在矩阵乘法中有左消去律:
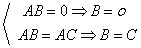
标准正交基 个
个 维线性无关的向量,两两正交,每个向量长度为1.
维线性无关的向量,两两正交,每个向量长度为1.

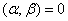 .
.
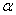 是单位向量
是单位向量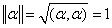 .
.
√ 内积的性质: ① 正定性: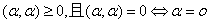
② 对称性: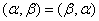
③ 双线性: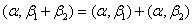
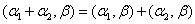
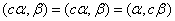
施密特  线性无关,
线性无关,
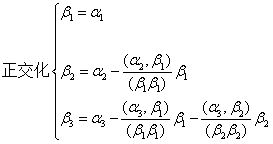
单位化: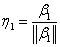
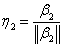
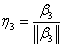
正交矩阵 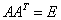 .
.
√  是正交矩阵的充要条件:
是正交矩阵的充要条件: 的
的 个行(列)向量构成
个行(列)向量构成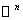 的一组标准正交基.
的一组标准正交基.
√ 正交矩阵的性质:① 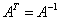 ;
;
② 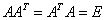 ;
;
③  是正交阵,则
是正交阵,则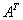 (或
(或 )也是正交阵;
)也是正交阵;
④ 两个正交阵之积仍是正交阵;
⑤ 正交阵的行列式等于1或-1.
 的特征矩阵
的特征矩阵 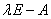 .
.
 的特征多项式
的特征多项式 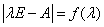 .
.
 的特征方程
的特征方程 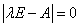 .
. 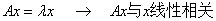
√ 上三角阵、下三角阵、对角阵的特征值就是主对角线上的 各元素.
各元素.
√ 若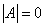 ,则
,则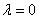 为
为 的特征值,且
的特征值,且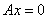 的基础解系即为属于
的基础解系即为属于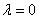 的线性无关的特征向量.
的线性无关的特征向量.
√ 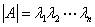
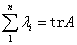
√ 若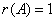 ,则
,则 一定可分解为
一定可分解为 =
=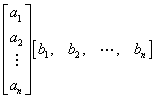 、
、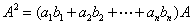 ,从而
,从而 的特征值为:
的特征值为: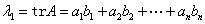 ,
, 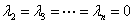 .
.
√ 若 的全部特征值
的全部特征值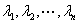 ,
,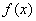 是多项式,则:
是多项式,则:
① 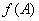 的全部特征值为
的全部特征值为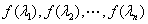 ;
;
② 当 可逆时,
可逆时, 的全部特征值为
的全部特征值为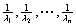 ,
,
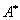 的全部特征值为
的全部特征值为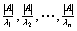 .
.
√ 
√ 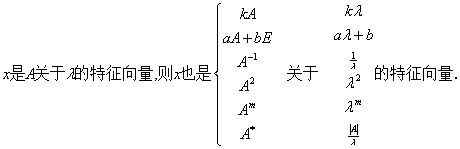
 与
与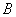 相似
相似 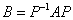 (
(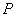 为可逆阵) 记为:
为可逆阵) 记为: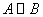
√  相似于对角阵的充要条件:
相似于对角阵的充要条件: 恰有
恰有 个线性无关的特征向量. 这时,
个线性无关的特征向量. 这时,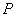 为
为 的特征向量拼成的矩阵,
的特征向量拼成的矩阵,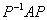 为对角阵,主对角线上的元素为
为对角阵,主对角线上的元素为 的特征值.
的特征值.
√  可对角化的充要条件:
可对角化的充要条件: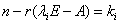
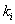 为
为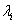 的重数.
的重数.
√ 若 阶矩阵
阶矩阵 有
有 个互异的特征值,则
个互异的特征值,则 与对角阵相似.
与对角阵相似.
 与
与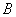 正交相似
正交相似 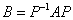 (
(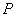 为正交矩阵)
为正交矩阵)
√ 相似矩阵的性质:① 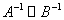 若
若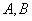 均可逆
均可逆
② 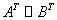
③ 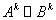 (
(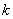 为整数)
为整数)
④ 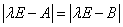 ,从而
,从而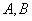 有相同的特征值,但特征向量不一定相同.即:
有相同的特征值,但特征向量不一定相同.即: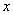 是
是 关于
关于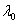 的特征向量,
的特征向量,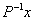 是
是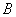 关于
关于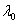 的特征向量.
的特征向量.
⑤ 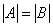 从而
从而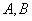 同时可逆或不可逆
同时可逆或不可逆
⑥ 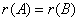
⑦ 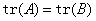
√ 数量矩阵只与自己相似.
√ 对称矩阵的性质:
① 特征值全是实数,特征向量是实向量;
② 与对角矩阵合同;
③ 不同特征值的特征向量必定正交;
④ 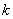 重特征值必定有
重特征值必定有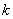 个线性无关的特征向量;
个线性无关的特征向量;
⑤ 必可用正交矩阵相似对角化(一定有 个线性无关的特征向量,
个线性无关的特征向量, 可能有重的特征值,重数=
可能有重的特征值,重数=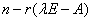 ).
).
二次型 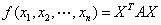
 为对称矩阵
为对称矩阵 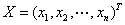
√ 用正交变换法化二次型为标准形:
① 求出 的特征值、特征向量;
的特征值、特征向量;
② 对 个特征向量单位化、正交化;
个特征向量单位化、正交化;
③ 构造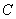 (正交矩阵),
(正交矩阵), ;
;
④ 作变换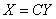 ,新的二次型为
,新的二次型为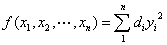 ,
, 的主对角上的元素
的主对角上的元素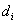 即为
即为 的特征值.
的特征值.
正定二次型 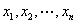 不全为零,
不全为零,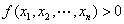 .
.
正定矩阵 正定二次型对应的矩阵.
√ 合同变换不改变二次型的正定性.
√ 成为正定矩阵的充要条件(之一成立):
① 正惯性指数为 ;
;
②  的特征值全大于
的特征值全大于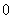 ;
;
③  的所有顺序主子式全大于
的所有顺序主子式全大于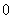 ;
;
④ 大于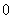 ).
).
√ 成为正定矩阵的必要条件: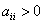 ;
; 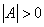 .
.
第二篇:20xx考研数学 线性代数超级总结-1
概念、性质、定理、公式必须清楚,解法必须熟练,计算必须准确 ?A可逆 ??r(A)?n
?A的列(行)向量线性无关 ??A的特征值全不为0
??Ax??只有零解 ? ?x??,Ax?? A?0?? n????R,Ax??总有唯一解
?ATA是正定矩阵 ??A?E
?A?pp???p p是初等阵12si???存在n阶矩阵B,使得AB?E 或 AB?E
注:全体n维实向量构成的集合R叫做n维向量空间. ○n
?A不可逆 ?r(A)?n ??A?0??A的列(行)向量线性相关
?0是A的特征值 ???Ax??有非零解,其基础解系即为A关于??0的特征向量
?r(aE?bA)?n ?注 aE?bA????(aE?bA)x??有非零解 ○
??=-a ?
向量组等价??矩阵等价(?)?具有?反身性、对称性、传递性 ????矩阵相似(?)?
矩阵合同(?)??
√ 关于e1,e2,???,en:
①称为?的标准基,?中的自然基,单位坐标向量p教材87;
②e1,e2,???,en线性无关; ③e1,e2,???,en?1;
④trE=n;
⑤任意一个n维向量都可以用e1,e2,???,en线性表示. nn
1
a11
Dn?
a12?a1na22?a2n?
?
an2?ann
?
j1j2?jn
a21?an1
?(?1)?(j1j2?jn)a1j1a2j2?anjn
√ 行列式的计算:
①行列式按行(列)展开定理:行列式等于它的任一行(列)的各元素与其对应的代数余子式的乘积之和. 推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.
AO
②若A与B都是方阵(不必同阶),则
OO
BA
==
A?
?A
OBBO
?
AO?
B
?AB
(拉普拉斯展开式)
BO
?(?1)mnAB
③上三角、下三角、主对角行列式等于主对角线上元素的乘积.
?
④关于副对角线:
a1n
a2n?1
?
?O
O
a2n?1
?an1
a1n
?(?1)O
n(n?1)a1na2n?an1 (即:所有取自不同行不
an1
同列的n个元素的乘积的代数和)
1x1
⑤范德蒙德行列式:x12
1x2
2x2?
???
1
2
???xi?xj?
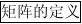
xn
1?j?i?n
?
xn
?x1n?1
n?1n?1x2?xn
?a11
?a21?由m?n个数排成的m行n列的表A?????am1
?A11?A12??????A1n
A21?A22?A2n
a12a22?am2
?a1n?
?
?a2n?
称为m?n矩阵.记作:A??aij?或Am?n

m?n??
?
?amn?
A?Aij
*
??
T
An1??
?An2?
,Aij为A中各个元素的代数余子式. ???
?Ann?
√ 逆矩阵的求法:
主?换位?ab?1?d?b?A
注: ?① A?1? ○ ????
ad?bc??ca?A副?变号?cd?
?
?1
2
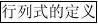
初等行变换
②(A?E)?????(E?A?1)
?a1
?③???
a2
?1
?a?1
??
???
?a3????
m
n
a2
????? ???a1??33?
(Am)n?(A)mn
a2
?1
?a1?
??
???
??1???1
1
a3
a2
??? ???
√ 方阵的幂的性质:AA?A
m?n
√ 设Am?n,Bn?s,A的列向量为?1,?2,???,?n,B的列向量为?1,?2,???,?s,
则AB?Cm?s
?b11b12?b1s???bb?b21222s???c,c,?,c??A??c ,(i?1,2,?,s)??为???1,?2,???,?n??12siii???????bb?bns??n1n2
Ax?ci的解?A??1,?2,???,?s???A?1,A?2,???,A?s???c1,c2,?,cs??c1,c2,?,cs可由?1,?2,???,?n线性表
示.即:C的列向量能由A的列向量线性表示,B为系数矩阵. 同理:C的行向量能由B的行向量线性表示,A为系数矩阵.
T
?a11
?a21?即: ????an1
a12a22?an2
?a1n???1??c1??a11?1?a12?2???a1n?2?c1
??????a??a????a??c?a2n???2??c2??2112222n22
? ??
???????????????????amn???n??cm??am1?1?am2?2???amn?2?cm
√ 用对角矩阵?左乘一个矩阵,相当于用?的对角线上的各元素依次乘此矩阵的行向量; 用对角矩阵?右乘一个矩阵,相当于用?的对角线上的各元素依次乘此矩阵的列向量. √ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘.
○○
○○
?AB??AT
√ 分块矩阵的转置矩阵:????T
CD???B
?A?1?A?
分块矩阵的逆矩阵:????
B???
?A?1?AC?????OB???O
?1?1
T
CT?
? DT?
?? ??B?1??B
A??
???1???A
?1?1
B?1?
? ?
?A?1A?1CB?1?O??AO?? ???1?1? ??
CBB?B?????BCA
?A11
分块对角阵相乘:A??
???B11,B???A22????A11B11
AB????
B22??n
?n?A11?,A??A22B22???
n?A22?
3
?A??BA*
分块对角阵的伴随矩阵:????B???*?? ??AB*??BA?????mn????(?1)BA*(?1)mnAB????
?
√ 矩阵方程的解法(A?0):设法化成(I)AX?B 或 (II)XA?B
(I)的解法:构造(A?B)?????(E?X)
初等行变换(II)的解法:将等式两边转置化为ATXT?BT,
用(I)的方法求出X,再转置得XT
① 零向量是任何向量的线性组合,零向量与任何同维实向量正交.
② 单个零向量线性相关;单个非零向量线性无关.
③ 部分相关,整体必相关;整体无关,部分必无关. (向量个数变动)
④ 原向量组无关,接长向量组无关;接长向量组相关,原向量组相关. (向量维数变动)
⑤ 两个向量线性相关?对应元素成比例;两两正交的非零向量组线性无关p教材114.
⑥ 向量组?1,?2,???,?n中任一向量?i(1≤i≤n)都是此向量组的线性组合.
⑦ 向量组?1,?2,???,?n线性相关?向量组中至少有一个向量可由其余n?1个向量线性表示.
向量组?1,?2,???,?n线性无关?向量组中每一个向量?i都不能由其余n?1个向量线性表示.
⑧ m维列向量组?1,?2,???,?n线性相关?r(A)?n;
m维列向量组?1,?2,???,?n线性无关?r(A)?n.
⑨ 若?1,?2,???,?n线性无关,而?1,?2,???,?n,?线性相关,则?可由?1,?2,???,?n线性表示,且表示法唯一. ⑩ 矩阵的行向量组的秩?列向量组的秩?矩阵的秩. 行阶梯形矩阵的秩等于它的非零行的个数.

可画出一条阶梯线,线的下方全为0;每个台阶只有一行,台阶数即是非零行的行数,阶梯线的竖线后面的第一个元素非零.当非零行的第一个非零元为

1,且这些非零元所在列的其他元素都是0? 矩阵的行初等变换不改变矩阵的秩,且不改变列向量间的线性关系;
矩阵的列初等变换不改变矩阵的秩,且不改变行向量间的线性关系.
即:矩阵的初等变换不改变矩阵的秩.
√ 矩阵的初等变换和初等矩阵的关系:
4
对A施行一次初等行变换得到的矩阵,等于用相应的初等矩阵左乘A;
对A施行一次初等列变换得到的矩阵,等于用相应的初等矩阵右乘A.
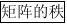
如果矩阵A存在不为零的r阶子式,且任意r?1阶子式均为零,则称矩阵A的秩为r.记作r(A)?r

向量组?1,?2,?,?n的极大无关组所含向量的个数,称为这个向量组的秩.记作r(?1,?2,?,?n

) A经过有限次初等变换化为B. 记作:A??B

?1,?2,???,?n和?1,?2,???,?n可以相互线性表示. 记作:??1,?2,???,?n?????1,?2,???,?n?
? 矩阵A与B等价?PAQ?B,P,Q可逆?r(A)?r(B),A,B为同型矩阵??A,B作为向量组等价,即:秩相
等的向量组不一定等价.
矩阵A与B作为向量组等价?r(?1,?2,???,?n)?r(?1,?2,???,?n)?r(?1,?2,????n,?1,?2,???,?n)?
矩阵A与B等价.
? 向量组?1,?2,???,?s可由向量组?1,?2,???,?n线性表示?AX?B有解○○○○
?r(?1,?2,???,?n)=r(?1,?2,????n,?1,?2,???,?s)?r(?1,?2,???,?s)≤r(?1,?2,???,?n).
? 向量组?1,?2,???,?s可由向量组?1,?2,???,?n线性表示,且s?n,则?1,?2,???,?s线性相关.
向量组?1,?2,???,?s线性无关,且可由?1,?2,???,?n线性表示,则s≤n.
? 向量组?1,?2,???,?s可由向量组?1,?2,???,?n线性表示,且r(?1,?2,???,?s)?r(?1,?2,???,?n),则两向量组等价;
p教材94,例10
? 任一向量组和它的极大无关组等价.向量组的任意两个极大无关组等价.
? 向量组的极大无关组不唯一,但极大无关组所含向量个数唯一确定.
? 若两个线性无关的向量组等价,则它们包含的向量个数相等.
? 设A是m?n矩阵,若r(A)?m,A的行向量线性无关;
若r(A)?n,A的列向量线性无关,即:?1,?2,???,?n线性无关.
√ 矩阵的秩的性质:
①若A?O?r(A)≥1 若A?O?r(A)?0 0≤r(Am?n)≤min(m,n) 5
②r(A)?r(AT)?r(ATA) p教材101,例15
③r(kA)?r(A) 若k?0 ④若Am?n,Bn?s,若r(AB)?0?? ⑤r(AB)≤min?r(A),r(B)? ?r(A)?r(B)?n B的列向量全部是Ax?0的解?
⑥若A可逆?r(AB)?r(B)
若B可逆?r(AB)?r(A) 即:可逆矩阵不影响矩阵的秩.
??Ax?? 只有零解???r(AB)?r(B) ⑦若r(Am?n)?n??; ???A在矩阵乘法中有左消去律?AB?O?B?O????AB?AC?B?C??
?r(AB)?r(B) 若r(Bn?s)?n?? B在矩阵乘法中有右消去律.?
⑧若r(A)?r?A与唯一的?
?Er?OO??Er等价,称??O??OO??为矩阵A的等价标准型. O?
6
