《线性代数及其应用》
一、行列式
1、余子式,代数余子式
2、几个定理(定理2.2,2.3,2.4)
按行展开: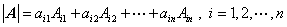
按列展开: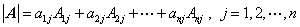
定理2.4 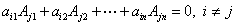 ;
;
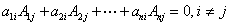 .
.
3、行列式的性质
(1) 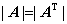 .
.
(2) 若行列式的某一列(行)可以拆成两列(行)之和,则行列式可以拆成两个行列式之和,即
 .
.
(2) 若行列式有两列(行)成比例,则行列式等于零.
(3) 初等变换性质
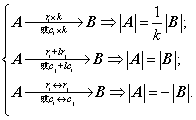
4、行列式计算:三角化法(性质);
降阶法(性质+展开定理);
范德蒙德、三对角行列式的结论.
5、分块矩阵的行列式
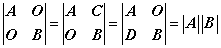
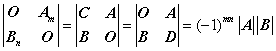
二、矩阵
1、矩阵及其运算(加法、数乘、乘法、幂、转置、方阵的行列式、分块运算)
(1) 乘法的结合律
(2) 方阵的幂的求解
(3) 转置的性质: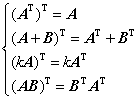
(4) 方阵的行列式: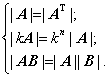
(5) 分块运算(转置、乘法--例3.13、3.14)
2、初等变换及初等矩阵
(1) 左行右列(矩阵的初等变换可用矩阵乘法来表示)

(2) 初等矩阵都是可逆的,且初等矩阵的逆仍是初等矩阵,即
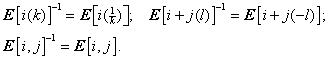
3、可逆矩阵
(1) 定义、性质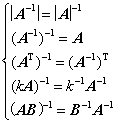
(2) 伴随矩阵 
(3) 判定: 可逆
可逆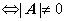
(4) 逆矩阵的求法 
(5) 分块矩阵的逆

(6) 矩阵方程的求解: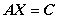 ,其中
,其中 可逆.
可逆.
法1  .
.
法2 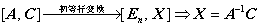 .
.
4、矩阵的秩与矩阵的相抵
(1) 矩阵的秩与性质(101页,105-107页)
① 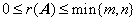 ;
;
② 子矩阵的秩不会超过原矩阵的秩;
③ 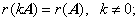
④ 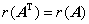 ;
;
⑤  ;
;
⑥ 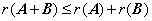 ;
;
⑦ 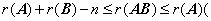 或
或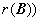 ;
;
若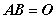 ,则
,则 ,其中
,其中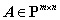 ,
,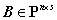 .
.
⑧ 设 ,则
,则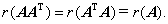
(2) 求矩阵的秩 (理论依据:矩阵的初等变换不改变矩阵的秩)
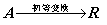 (行阶梯形矩阵),
(行阶梯形矩阵),
则 的非零行的个数.
的非零行的个数.
(3) 矩阵的相抵(等价)
① 
②  ,其中
,其中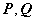 可逆.
可逆.
③ 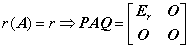 或
或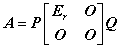 .
.
三、线性空间
1、向量组的线性相关性的判断(命题4.2、4.3、4.4、4.5、定理4.1、4.2、4.4)
(1) 证明方法--
(2) 基本结论
判断向量组线性相关(命题4.2,命题4.3(2),定理4.1及推论1,定理4.2)
充要: 线性相关
线性相关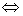 其中至少有一个向量可由其余向量线性表示.
其中至少有一个向量可由其余向量线性表示.
充分: 线性相关
线性相关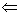

判断向量组线性无关(命题4.3(3),命题4.4的推论)
2、等价向量组
(1) (Ⅰ)可由(Ⅱ)线性表示,则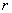 (Ⅰ)
(Ⅰ) 
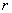 (Ⅱ).
(Ⅱ).
(2) (Ⅰ)与(Ⅱ)等价,则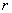 (Ⅰ)
(Ⅰ) (Ⅱ).
(Ⅱ).
3、子空间的验证
(1) 非空、加法和数量乘法的封闭;
(2) 命题4.1(生成子空间)--例4.9,例4.35
4、向量组的秩及极大无关组(命题4.6,定理4.4及推论2)、(线性)子空间的基与维数
(1) 写成列向量作初等行变换,确定向量组的秩与极大无关组.
(2) 对于 ,则
,则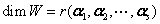 , 即生成子空间的维数
, 即生成子空间的维数
与基就是向量组 的秩与极大无关组.
的秩与极大无关组.
5、坐标的概念、基变换公式与坐标变换公式
坐标: 在基
在基 下的坐标
下的坐标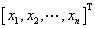 .
.
基变换公式:
坐标变换公式:
 或
或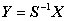
四、线性方程组(含参量、不含参量)
1、解的情况
(1) 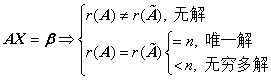
若 是方阵,则
是方阵,则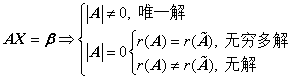
(2) 齐次线性方程组 有非零解
有非零解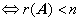 .
.
若 是方阵,则齐次线性方程组
是方阵,则齐次线性方程组 有非零解
有非零解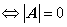 .
.
2、解的结构
齐次 :
:
(1) 解空间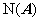 、
、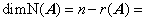 基础解系所含向量的个数
基础解系所含向量的个数
(2) 基础解系不唯一,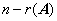 的线性无关的解均可作为
的线性无关的解均可作为 的一个基础解系.
的一个基础解系.
(2) 结构式:通解=基础解系的任意线性组合
非齐次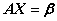 :
:
(1) 非-非=齐
(2) 结构式:通解=特解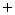 导出组
导出组 的通解
的通解
五、线性变换
1、线性变换的验证 (定义5.4)
2、线性变换在一个基下的矩阵(定义5.7)、命题5.8

3、线性变换在不同基下的矩阵之间的关系(相似) 定理5.9
六、内积空间
1、内积的概念、长度、正交(正交向量组必线性无关)
2、施密特正交化
3、正交矩阵
(1) 定义、性质;
(2)  阶实矩阵
阶实矩阵 是正交矩阵的充要条件是
是正交矩阵的充要条件是 的列(行)向量组是
的列(行)向量组是 的一个标准正交基. (命题6.2)
的一个标准正交基. (命题6.2)
七、矩阵的相似对角形
1、特征值和特征向量的定义、性质
(1)  ;
;
(2)  与
与 具有相同的特征值(特征向量未必相同);
具有相同的特征值(特征向量未必相同);

(3)
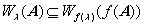 ;
; .
.
(4) 属于不同特征值的特征向量线性无关(定理5.3、定理5.4及推论).
2、相似矩阵的定义、性质(秩、行列式、迹、特征值相等,但特征向量未必相同)
相似的判定:若 与
与 可对角化(实对称矩阵),且
可对角化(实对称矩阵),且 与
与 具有相同的特征值,则
具有相同的特征值,则 与
与 相似.
相似.
若 与
与 相似,则矩阵多项式
相似,则矩阵多项式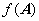 与
与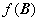 也相似.
也相似.
3、矩阵的相似对角化
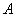 可对角化
可对角化
 有
有 个线性无关的特征向量
个线性无关的特征向量
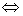 数域
数域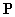 内有
内有 个特征值,每一个特征值的几何重数等于代数重数
个特征值,每一个特征值的几何重数等于代数重数
(充分条件)  有
有 个互不相同的特征值
个互不相同的特征值
 可对角化
可对角化
4、实对称矩阵
(1) 特征值: 阶实对称矩阵有
阶实对称矩阵有 个实特征值.
个实特征值.
(2) 特征向量:实对称矩阵的属于不同特征值的特征向量正交.
(3) 实对称矩阵必正交相似于实对角矩阵(几何重数等于代数重数).
(4) 若 与
与 均为实对称矩阵,则
均为实对称矩阵,则 与
与 正交相似(相似)
正交相似(相似)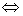
 与
与 具有相同的特征值.(正交相似
具有相同的特征值.(正交相似 既相似,又合同)
既相似,又合同)
八、二次型
1、二次型的矩阵及秩(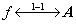 (对称))
(对称))
2、矩阵的合同:合同必相抵;
正交相似 既相似,又合同
既相似,又合同
实对称矩阵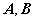 合同
合同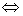
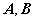 的正惯性指数与秩相同
的正惯性指数与秩相同
3、化二次型为标准形(不唯一)--正交替换法、配方法(满秩线性替换)
4、惯性定理:实二次型的规范形唯一(正、负惯性指数,符号差)
5、正定二次型
(1) 判定:① 定义;
②  的特征值都大于零(
的特征值都大于零( 的正惯性指数等于
的正惯性指数等于 );
);
③  与
与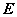 合同(与正定矩阵
合同(与正定矩阵 合同的实对称矩阵
合同的实对称矩阵 正定);
正定);
④ 存在可逆矩阵 ,使得
,使得 ;
;
⑤  的所有顺序主子式都大于零
的所有顺序主子式都大于零
(2) 必要条件: ;
;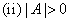
第二篇:线性代数学习总结
数学四 线 性 代 数 总 结
一、 行列式
1.n阶行列式的概念 a11 a12 …… a1n (1) n阶行列式的递归定义 a21 a22 …… a2n
有n ^ 2个数组成的n阶列式是一个算式,当 ……………… n=1时 an1 an2 …… ann
la11l=a11。当n≥2时
n
D=a11A11 + a12A12 + … + a1A1n=∑a1j A1j j=1
其中A1j=( -1 ) ^ 1+ j M1j ,为a1j的代数余子式。 a21… a2j-1 a2j+1… a2n a31… a3j-1 a3j+1… a3n
为a1j的余子式。 …………………… an1… anj-2 an j+1… ann
(2) n阶行列式的逆序定义
a11 a12 …… a1n
a21 a22 …… a2n
∑( -1 )^σ(i1,i2…in) a1i1 a2i2…anin ………………
an1 an2 …… ann (i1,i2…in)
2.行列式的性质
性质一 行列式的行和列互换后,行列式的值不变。
性质二 行列式的两行(或两列)互换,行列式改变符号。
推论 如果行列式中有两行(或列)的对应元素相同,则此行列式为零。 性质三 用数k乘以行列式的一行(列),等于以数k乘以此行列式。
推论 如果行列式某行(列)的所有元素的公因子,则公因子可以提到行 列式外面。
推论 如果行列式有两行(或两列)的对应元素成比列,则行列式等于零。 推论 如果行列式中以行(或一列)全为零,则行列式的值必为零。
性质四 如果行列式中的某行(或某列)均为两项之和,则行列式等于两个行列式之和。
推论 如果将行列式某一行(或某一列)的每一个元素都写成M(M≥2)个元素的和,则此行列式可以写成M个行列式的和。
性质五 将行列式的某一行(列)的每一个元素同乘以数k后加于另一行(列)对应位置的元素上,行列式的值不变。
性质六 如果行列式中某行(或列)中各元素是其余各行(或各列)分别乘一常数后各对应元素之和,则行列式的值为零。
性质七 行列式的任何一行(或列)的元素于另一行(或列)的对应元素的代数余子式的乘积之和必为零。
ai1Aj1 + ai2Aj2 + … +a1nAjn = 0 ( i≠j )
3.拉普拉斯展开式
行列式按k行(或列)展开,则 c
D = ∑ MiAi ( Mi为k阶子式,Ai为k阶代数余子式)
i=1
4. 利用拉普拉斯展开式的两种特殊情况
a11 … a1n 0 … 0 ………………………… a11 … a1n an1 … ann 0 … 0 ………… c11 … c1n b11 … b1n an1 … ann …………………………
cm1 …cmn bm1 …bmn
0 … 0 a11 … a1n ………………………… … ann =( -1 )^(mn) 0 … 0 a n1
c11 … c1n b11 … b1n ………………………… cm1…cmn bm1 …bmn
5. 重要公式及结论
b11 … b1n …………… bm1 …bmn
a11 … a1n …………… an1 … ann b11 … b1n …………… bm1 …bmn
(1)如果A,B均为n阶矩阵,则lABl = lAllBl,但AB≠BA。 (2) 如果A,B均为n阶矩阵,则lA±Bl ≠ lAl±lBl。 (3) 如果A为n阶矩阵,则lkAl = k^n lAl。 (4) 如果A为n阶矩阵,则lAl = lA′l
(5) 如果A为n阶可逆矩阵,则lAˉ;ˉ l =k^n / lAl 。 (6) 如果A*为A的伴随矩阵,则lA*l = lAl^(n-1)
lAl ( i = j )
(7) 如果A为n阶矩阵,则ai1Aj1 + ai2Aj2 + … +a
0 ( i≠j )
A C A O O A
(8) O B = lAl lBl ;( -1 )^(mn) lAl C B B O
O A
B C
=( -1 )^(mn) lAl lBl。
(9) a11 X a11 O a22 a22
= = O ann X ann
=a11 a22 … ann 。
O a1n O a1n 2n-1 = a 2n-1 = a an1 O an1 X
a11 O a22
O ann
X a1n a2n-1
an1 O
=( -1 ) ^ [n (n+1) / 2] a1n a2n-1 … an1 。 (10) 范德蒙行列式
1 1 1 … 1
a1 a2 a3 … an
a1^2 a2^2 a3^2 … an^2 = ∏ ( aj – ai ) 其中 ( ai≠aj) (i≠j) …………………………… 1≤i≤j≤n
a1^n-1 a2^n-1 a3^n-1 … an^n-1
6. 行列式的求值方法
(1)一般行列式的求值方法
将行列式化为上、下三角行列式;
将行列式中一列的其余元素化为零,在按该列展开,不断降阶计算; (2)n阶行列式的求值方法
行列式中较多元素是零时,利用行列式的定义计算;
当各行(或列)诸元素之和相等时,可将各行(或列)加到同一行(或列)中去; 各行(或列)加减同一行(或列)的倍数,适用于可变为三角形式或提取公因子的; 观察一次因式法; 升阶法; 降阶法; 拆项法;
递归法(归纳法);
