第一章 行列式
线性方程组的求解是线性代数的一个重要课题。行列式是由研究线性方程组产生的,它是一个重要的数学工具,它在数学及其他学科中都有着广泛的应用。
本章的教学基本要求:了解行列式的定义和性质,掌握利用行列式的性质及按行(列)展开定理计算行列式的方法,会计算简单的n阶行列式。理解和掌握克拉默(Cramer)法则。
本章的重点及难点:利用行列式的性质及按行(列)展开定理计算行列式的值,主要是三阶、四阶行列式的计算;利用克拉默法则求解线性方程组。
§ 1 二阶、三阶行列式
一、内容提要
1.二阶行列式的定义

其中 称为行列式的元素,
称为行列式的元素, 的两个下标表示该元素在行列式中的位置,第一个下标称为行标,表明该元素位于第i行;第二个下标称为列标,表明该元素位于第j列。
的两个下标表示该元素在行列式中的位置,第一个下标称为行标,表明该元素位于第i行;第二个下标称为列标,表明该元素位于第j列。
二阶行列式中,等式右端的表达式又称为行列式的展开式,二阶行列式的展开式可以用所谓对角线法则得到,即:



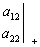 =
=
其中,实线上两个元素的乘积带正号,虚线上两个元素的乘积带负号,所得两项的代数和就是二阶行列式的展开式。
2.三阶行列式的定义


三阶行列式的展开式也可以用对角线法则得到,三阶行列式的对角线法则如下图所示:


其中每一条实线上三个元素的乘积带正号,每一条虚线上三个元素的乘积带负号,所得六项的代数和就是三阶行列式的展开式。
二、例题分析
例1 求解二元线性方程组

解: 由于系数行列式 

 ,
, 
所以方程组有唯一解为:  ,
,  。
。
例2 计算行列式 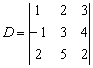
解 

例3 计算行列式
 ;
; ;
;  ;
; 
解: 由对角线法则有:  ;
;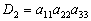 ;
;
 ;
;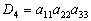
特别地: 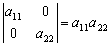 ;
; 
三、小结
对角线法则只适用与二阶与三阶行列式的计算。
由例3得结论:
(1)上(下)三角行列式等于主对角线上元素的乘积。
(2)对角行列式等于主对角线上元素的乘积。
§ 2 全排列及其逆序数
一、内容提要
排列 把 n个不同的元素排成一列,叫做这 n个元素的全排列,简称排列.
n个不同元素的所有排列的种数,通常用 表示.
表示.
 。
。
逆序 在一个排列 中,若
中,若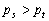 ,则称这两个数组成一个逆序.
,则称这两个数组成一个逆序.
逆序数 排列 中,所有逆序的总数称为此排列的逆序数。记为
中,所有逆序的总数称为此排列的逆序数。记为 。
。
排列 中,考虑元素
中,考虑元素 ,如果比
,如果比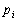 大的且排在
大的且排在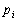 前面的元素有
前面的元素有 个,则称元素
个,则称元素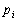 的逆序数是
的逆序数是 。记为
。记为 。
。
奇排列 逆序数为奇数的排列称为奇排列。
偶排列 逆序数为偶数的排列称为偶排列。
特别地,标准排列1,2,···,n的逆序数 。
。
规定,标准排列是偶排列。
二、例题分析
排列 中,考虑比
中,考虑比 大,且排在
大,且排在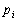 前面的元素的个数,就可以排列的逆序数。即
前面的元素的个数,就可以排列的逆序数。即
 (
( 前面比
前面比 大的数的个数)+(
大的数的个数)+( 前面比
前面比 大的数的个数)+ ···
大的数的个数)+ ···
··· + ( 前面比
前面比 大的数的个数)
大的数的个数)
 ;
;
同样,考虑比 小,且排在
小,且排在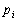 后面的元素的个数,就可以排列的逆序数。即
后面的元素的个数,就可以排列的逆序数。即
 (
( 后面比
后面比 小的数的个数)+(
小的数的个数)+( 后面比
后面比 小的数的个数)+ ···
小的数的个数)+ ···
··· + (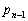 后面比
后面比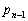 小的数的个数)。
小的数的个数)。
例4 求下列排列的逆序数,并确定它们的奇偶性。
(1)5 3 2 1 4; (2)n (n–1) ···2 1; (3)(2k) 1 (2k–1) 2 (2k–2) 3 (2k–3) ··· ( k+1) k。
解:(1)5 3 2 1 4
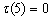 ,
, ,
,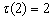 ,
,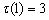 ,
, 。
。
因此, 。此排列为奇排列。
。此排列为奇排列。
(2)n (n–1) ···2 1
 ,
, ,
,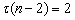 ,···,
,···, ,
, ,
, 。
。
因此, 。
。
当 时,排列为偶排列;
时,排列为偶排列;
当 时,排列为奇排列。
时,排列为奇排列。
(3)(2k) 1 (2k–1) 2 (2k–2) 3 (2k–3) ··· ( k+1) k
 ,
, 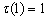 ,
,  ,
,
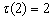 ,
,  ,
,
······, ······,
 ,
, 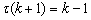 ,
,  。
。
因此,

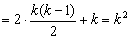 。
。
当k为偶数时,排列为偶排列;
当k为奇数时,排列为奇排列。
例5 设 的逆序数为k,问排列
的逆序数为k,问排列 的逆序数是多少?
的逆序数是多少?
解:若在排列 中,
中,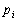 后面比
后面比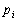 小的数共有
小的数共有 个
个 ,则在排列
,则在排列 中,
中,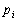 前面的数共有
前面的数共有 个,
个,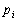 前面比
前面比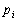 大的数共有
大的数共有 个
个 。由已知有
。由已知有
 。
。
所以排列 的逆序数为
的逆序数为

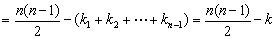 。
。
三、小结
求排列 的逆序数的方法:
的逆序数的方法:
(1) (
( 前面比
前面比 大的数的个数)+(
大的数的个数)+( 前面比
前面比 大的数的个数)+ ···
大的数的个数)+ ···
··· + ( 前面比
前面比 大的数的个数)
大的数的个数)
 ;
;
(2) (
( 后面比
后面比 小的数的个数)+(
小的数的个数)+( 后面比
后面比 小的数的个数)+ ···
小的数的个数)+ ···
··· + (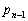 后面比
后面比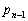 小的数的个数)。
小的数的个数)。
§ 3 n阶行列式的定义
一、内容提要
由n2个元素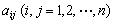 组成的记号
组成的记号

称为n阶行列式。其值等于所有取自不同行不同列的n个元素的乘积的代数和,各项的符号是:当这一项中的n个元素的行标排成标准排列后,若对应的列标构成的排列为偶数,则取正号;若对应的列标构成的排列为奇数,则取负号,即
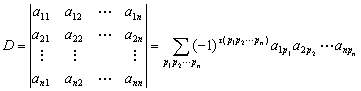 。
。
行列式简记为 。
。
一阶行列式为 。
。
n阶行列式中,等式右端的表达式又称为行列式的展开式,
二、例题分析
例6 判别 和
和 是否为六阶行列式中的项。
是否为六阶行列式中的项。
分析:判别是否为n阶行列式中的项,要考虑:
(1)n个元素是否位于不同行,不同列;
(2)确定其符号。
解: 不是六阶行列式中的项。
不是六阶行列式中的项。
这是因为, 与
与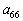 都位于第6列。
都位于第6列。
 是六阶行列式中的项。
是六阶行列式中的项。
首先, 中的6个元素位于不同行,不同列;再有,
中的6个元素位于不同行,不同列;再有,
 。
。
确定其符号: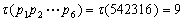 ,因此,应带负号。
,因此,应带负号。
N阶行列式的展开式是n!项的代数和,每项都是位于不同行不同列的n个元素的乘积。因此,对于含零元素较多的行列式,可直接用定义计算。但对于一般性的行列式,常用后面将要学到的性质与定理进行简化计算。
对于含零元素较多的行列式,用定义计算时,只需求出所有非零项,并进行代数和即可。
例7 计算行列式  。
。
解:这是一个4阶行列式。其展开式中项的一般形式为 。
。
若 ,则
,则 ,从而
,从而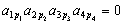 。所以,只有
。所以,只有 才可能不为零。
才可能不为零。
同理,要使 ,必须
,必须 ,
,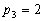 ,
, 。
。
即行列式的展开式中不为零的项仅为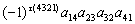 。因此,
。因此,

 。
。
例8 计算行列式
 。
。
解:这是一个1998阶行列式。
显然,在所有取自不同行不同列的1998个元素乘积 中,只有
中,只有

因此, 

 。
。
例9 利用行列式定义,证明
 。
。
证:由行列式定义知其值是n!项的代数和,每项是不同行不同列的n个元素的积。上述行列式中,除主对角元素乘积一项是奇数1外,其余各项(共n! -1项)的每项中至少有一个2,故均是偶数。n! –1个偶数之代数和仍是偶数。再和1相加,不可能是零。因此
 。
。
三、小结
1.行列式的实质是一种特定的算式,计算结果是一个数;
2.n阶行列式的展开式是n!项的代数和,每项都是位于不同行不同列的n个元素的乘积;
3. 项前面的符号为
项前面的符号为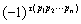 ;
;
4.对角线法则不适用于四阶及四阶以上的行列式展开式;
5.几个常用行列式结果:
(1)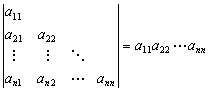 ,
,
(2) ,
,
(3) 。
。
§ 4 对 换
一、内容提要
在排列中,将任意两个元素对调,其余的元素不动,这种作出新排列的手续叫做对换。将相邻两个元素对换,叫做相邻对换。
定理1 一个排列中任意两个元素对换,排列改变奇偶性。
推论 奇排列调成标准排列的对换次数为奇数,偶排列调成标准排列的对换次数为偶数。
定理2 n 阶行列式也可定义为
 。
。
二、小结
行列式的两种定义,

 。
。
行列式更一般的定义为
 。
。
其中  。
。
§ 5 行列式的性质
一、内容提要
1.性质
性质1 行列式与它的转置行列式相等,即 。
。
性质2 互换行列式的两行(列),行列式变号。
以 表示行列式的第i行,以
表示行列式的第i行,以 表示第i列。
表示第i列。
互换第i行与第j行,记作 ;互换第i列与第j列,记作
;互换第i列与第j列,记作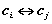 。
。
推论 如果行列式有两行(列)完全相同,则行列式为零。
性质3 行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘以此行列式。
即  ,
,
或  。
。
第i行乘以k,记作 ;第i列乘以k,记作
;第i列乘以k,记作 。
。
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。
第i行提出公因子k,记作 ;第i列提出公因子k,记作
;第i列提出公因子k,记作 。
。
性质4 行列式中如果有两行(列)元素成比例,则此行列式为零。
性质5 如果行列式的某一列(行)元素都是两数之和,例如第i列的元素都是两数之和:
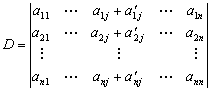 ,
,
则D等于下列两个行列式之和
 。
。
如果第i行的元素都是两数之和:
 ,
,
则D等于下列两个行列式之和
 。
。
性质6 把行列式的某一列(行)各元素乘以同一数,然后加到另一列(行)对应的元素上去,行列式不变。
例如,以数k乘第i列加到第j列(记作 )有
)有


以数k乘第i行加到第j行(记作 )有
)有

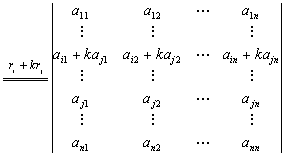 。
。
2.常用结论:
如果  ,
,  ,
,  。
。
则,
常记为  。
。
二、例题分析
例10 计算上三角行列式(主对角线以下元素全为0)

解: 利用性质1,得
 。
。
例11 计算  。
。
解  。
。
(第二、三行元素成比例)
例12 计算  。
。
解:由性质5有 
右边第一个行列式中,第一列乘 加到第2、3列;在第二个行列式的第一列中提出
加到第2、3列;在第二个行列式的第一列中提出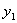 得
得

 。
。
例13 计算  。
。
分析:首先,利用性质将行列式化为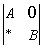 型,再利用
型,再利用 求出结果。
求出结果。
解:

 。
。
三、小结
(1)行列式的六个性质、两个推论是计算行列式的理论保证,要尽快熟练掌握它们。
(2) 。
。
§ 6行列式按行(列)展开
一、内容提要
在n阶行列式中,划去 所在的第i行和第j列的元素,剩余的元素按原有次序构成的
所在的第i行和第j列的元素,剩余的元素按原有次序构成的 阶行列式,称为元素
阶行列式,称为元素 的余子式,记为
的余子式,记为 。
。
 称为
称为 的代数余子式。
的代数余子式。
定理3 n 阶行列式 等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即
等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即  ;
;
或  。
。
推论 行列式某一行(列)的元素与另一行(列)的对应元素代数余子式乘积之和等于
零。即  ,
,
或  。
。
综合定理及推论,有展开式

或 
其中 
二、例题分析
在实际计算时,直接用定理展开行列式,通常并不能减少计算量,除非行列式中某一行(列)含有较多的0元素。因此,在具体计算时,我们总是先运用行列式的性质,将某一行(列)元素尽可能多地化为0,然后再利用定理,按该行(列)展开。
例14 计算行列式
 。
。
解:


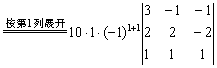

 .
.
下面通过例题介绍利用性质、定理计算行列式的几种常用方法。
1.化为上三角行列式法
利用性质,把行列式化为上三角行列式,是计算行列式的基本方法。
例15 计算行列式

解: 

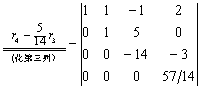

在化为上三角行列式时,要从第一列开始,一列一列进行。在化第i列时,利用性质2选择好 ,以便化
,以便化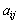 (
( )为0时,尽量避免出现分数,减少计算量。
)为0时,尽量避免出现分数,减少计算量。
例16 计算 
解: 

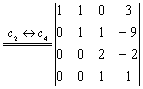
 = 4
= 4
观察行列式,抓住其特点,是快速准确计算行列式的第一保证。
例17 计算 
分析: 这个行列式有一个特点,各列4个数之和都是6。因此,把第2、3、4行都加到第一行,提出公因子6,然后再化简:
解:
 = 48。
= 48。
例18 计算 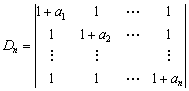 ,其中
,其中 。
。
解:从第1行到第n行,依次提出公因子 ,得
,得


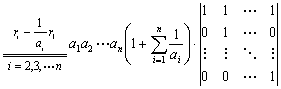
 。
。
2.拆分法
根据行列式的特点,利用性质5将行列式进行拆分计算。
例19 证明: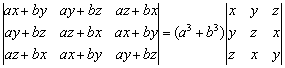 。
。
证:左边



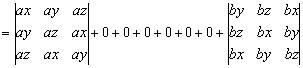

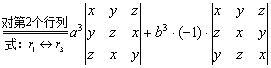

 .
.
例20计算行列式  。
。
解:按第1列拆分,


 。
。
3.递推公式法
有时,根据行列式的特点,得到递推公式,计算出行列式。
例21 计算 
解: 按第一列展开,得
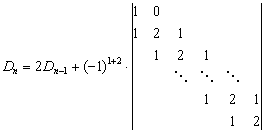
将右端第二项的行列式按第一行展开,得

即 
由此递推得 
于是 

从而 
4.数学归纳法
数学归纳法也是计算行列式的常用方法。
例22 证明行列式
 。
。
证:对阶数n使用数学归纳法。
当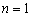 时,
时, ,故结论成立。
,故结论成立。
假设结论对 的自然数都成立,下面要证对n也成立。为此将
的自然数都成立,下面要证对n也成立。为此将 按第1列展开,得
按第1列展开,得

上式右端的第1个行列式为 ,而第2个行列式按第1行展开其值为
,而第2个行列式按第1行展开其值为 ,所以有
,所以有



 。
。
计算行列式要充分利用已知结果。
例23 计算行列式
解:从第 行开始,第
行开始,第 行经过
行经过 次相邻对换,换到第1行,第
次相邻对换,换到第1行,第 行经
行经 次对换换到第2行…,经
次对换换到第2行…,经 次行交换,得
次行交换,得
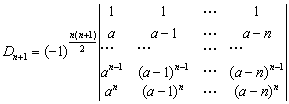
此行列式为范德蒙德行列式
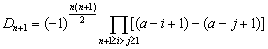
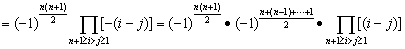

计算行列式,还应多进行一题多解。
例24证明:
 。
。
解法1:用数学归纳法证明
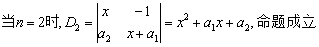
假设对于 阶行列式命题成立.
阶行列式命题成立.
即 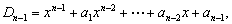



所以,对于 阶行列式命题成立.
阶行列式命题成立.
解法2:用递推法。
将 按第1列展开,得
按第1列展开,得


由此得递推公式:  。于是,
。于是,
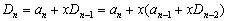

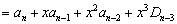

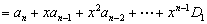

 。
。
解法3:




 .
.
解法4:将行列式按第n行展开也可以,读者自己试一试。
三、小结
行列式的计算方法灵活多样,技巧性强,前面所举例子的解法只是众多方法中的几种。读者可以想象并总结出另一些方法和技巧进行计算,并比较各种作法的繁简,逐步提高计算能力。
*补充 拉普拉斯(Laplace)定理
§6中的按行(列)展开定理只是把行列式按某一行(列)展开,下面再把它推广到按k行(k列)展开。首先应把元素的余子式和代数余子式的概念加以推广。
定义 在n阶行列式中,任取k行 与k列
与k列 ,将这些行与列相交处的元素按原来相对位置构成的k阶行列式
,将这些行与列相交处的元素按原来相对位置构成的k阶行列式
 ,
,
称为该行列式的一个k阶子式,记为N。划去这些行和列后所剩下的元素依原次序构成的一个 阶子式,称为N的余子式,记为M。称
阶子式,称为N的余子式,记为M。称 为N的代数余子式。
为N的代数余子式。
例如,对四阶行列式 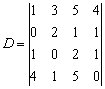
取第2、第3行与第2、第4列,得到一个二阶子式  。
。
N的余子式为 。
。
N的代数余子式为 。
。
一般在n阶行列式中取定k行,就有 个k阶子式。
个k阶子式。
定理(Laplace定理)在n阶行列式D中,任取k行(列),则由这k行(列)元素所有的k阶子式与其对应的代数余子式的乘积之和等于行列式D。
设取定的k行的所有子式为N1,N2,…,Nt,其所对应的代数余子式分别为A1,A2,…,At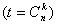 ,则
,则

例1 用拉普拉斯定理计算

解: 选取第1、2行,只有3个非零二阶子式
 ,
,  ,
,  ,
,
其对应的代数余子式为
 ,
, 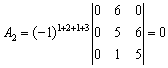 ,
,
 。
。
故 
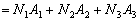 。
。

例2 计算2n阶行列式

解: 选取第n,n+1行应用拉普拉斯定理,只有一个非零二阶子式
 ,
,
其代数余子式为

故 
利用这个递推公式及 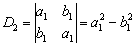 ,得
,得



 。
。
§ 7克拉默法则
一、内容提要
克拉默法则 如果n元线性方程组
 (*)
(*)
的系数行列式不等于零,即

则方程组(*)有唯一解,且其解为
 ,
, ,…,
,…,
其中 是把
是把 的第j列各元素依次换成方程组的常数项所得到的n阶行列式,即
的第j列各元素依次换成方程组的常数项所得到的n阶行列式,即
 , ( j=1, 2 , … , n )
, ( j=1, 2 , … , n )
定理4 如果n元线性方程组(*)的系数行列式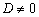 ,则方程组(*)一定有解,且解是唯一的。
,则方程组(*)一定有解,且解是唯一的。
定理4ˊ如果n元线性方程组(*)无解或有两个不同的解,则它的系数行列式必为零。
定理5 如果齐次线性方程组
 (**)
(**)
的系数行列式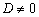 ,则齐次方程组(**)只有零解。
,则齐次方程组(**)只有零解。
定理5ˊ如果齐次线性方程组(**)有非零解,则它的系数行列式必为零。
二、例题分析
例25 求下列线性方程组的解

解:该方程组的系数行列式为范德蒙德行列式


 。
。
方程组有唯一解。容易看出,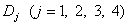 也是范德蒙德行列式:
也是范德蒙德行列式:

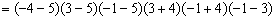
 ;
;

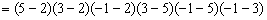
 ;
;


 ;
;
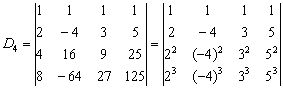

 。
。
故方程组的解为
 ,
, ,
, ,
,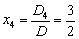 。
。
例26 讨论 为何值时,齐次线性方程组有唯一零解。
为何值时,齐次线性方程组有唯一零解。

解:方程组的系数行列式
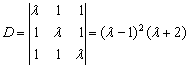
由此可知,当 且
且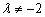 时,D≠0。此时,方程组有唯一零解。
时,D≠0。此时,方程组有唯一零解。
例27 给定平面上三个点(1,1),(2,–1),(3,1),求过这三个点且对称轴与Y轴平行的抛物线方程。
解: 因为抛物线的对称轴与Y轴平行,因此可设所求抛物线方程为  ,
,
于是有

这是以 为未知量的三元线性方程组,其系数行列式
为未知量的三元线性方程组,其系数行列式


最右边的行列式是范德蒙德行列式,所以
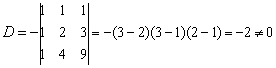
所以方程组有唯一解。
易得  ,
,
 ,
,
 。
。
故  ,
, ,
,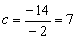
即所求抛物线方程为  。
。
三、小结
克拉默法则是线性方程组理论的一个很重要结果,它不仅给出了方程组(*)有唯一解的条件,并且给出了方程组的解与方程组的系数和常数项的关系,在后面的讨论中,还会看到它在更一般的线性方程组的研究中也起着重要的作用。
克拉默法则求解线性方程组必须满足如下两个条件:
(1)方程组中方程的个数与未知量的个数相同;
(2)方程组的系数行列式 。
。
习题一
(A组)
1.利用对角线法则计算下列行列式:
(1)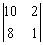 ; (2)
; (2) ;
;
(3) ; (4)
; (4)
2.用行列式解下列方程组:
(1) , (2)
, (2) 。
。
3.求下列排列的逆序数,并确定它们的奇偶性。
(1)2 1 7 9 8 6 3 5 4 ; (2)2 4 6 ··· 2 n (2n –1) (2n –3) ··· 3 1 。
4.在6阶行列式中, ,
, 这两项应带什么符号?
这两项应带什么符号?
5.计算下列行列式
(1)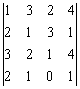 ; (2)
; (2)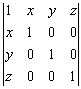 ;
;
(3) ; (4)
; (4) ;
;
(5) ; (6)
; (6) 。
。
6.用克莱姆法则解下列方程组:
(1) ; (2)
; (2) 。
。
(B组)
7.填空题:
(1)如果n阶行列式中,负项的个数为偶数,则n 。
。
(2)如果n阶行列式中等于零的元素个数大于 ,那么,此行列式的值为 。
,那么,此行列式的值为 。
(3)设 ,则
,则 。
。
(4)设 ,则
,则 。
。
(5)设 ,则
,则
 。
。
(6)设 ,则
,则
 。
。
8.计算下列行列式:
(1) ; (2)
; (2) ;
;
(3)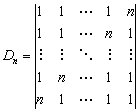 ; (4)
; (4) ;
;
(5) 。
。
