线性代数全公式
基本运算
①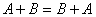
②
③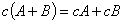
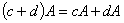
④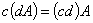
⑤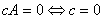 或
或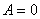 。
。


 。
。
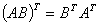
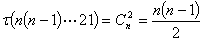
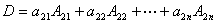
转置值不变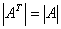
逆值变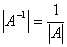
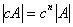
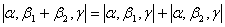
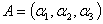 ,3阶矩阵
,3阶矩阵
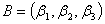
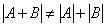
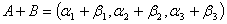
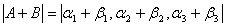


有关乘法的基本运算

线性性质 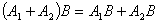 ,
,
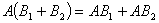
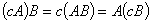
结合律 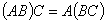
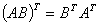
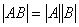
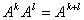

 不一定成立!
不一定成立!
 ,
,
 ,
,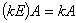
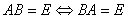
与数的乘法的不同之处
 不一定成立!
不一定成立!
无交换律 因式分解障碍是交换性
一个矩阵 的每个多项式可以因式分解,例如
的每个多项式可以因式分解,例如
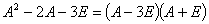
无消去律(矩阵和矩阵相乘)
当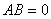 时
时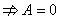 或
或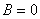
由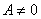 和
和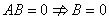
由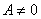 时
时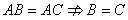 (无左消去律)
(无左消去律)
特别的 设 可逆,则
可逆,则 有消去律。
有消去律。
左消去律: 。
。
右消去律: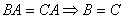 。
。
如果 列满秩,则
列满秩,则 有左消去律,即
有左消去律,即
①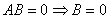
②
可逆矩阵的性质
i)当 可逆时,
可逆时,
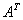 也可逆,且
也可逆,且 。
。
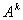 也可逆,且
也可逆,且 。
。
数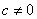 ,
, 也可逆,
也可逆,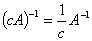 。
。
ii) ,
,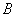 是两个
是两个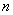 阶可逆矩阵
阶可逆矩阵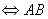 也可逆,且
也可逆,且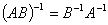 。
。
推论:设 ,
,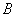 是两个
是两个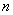 阶矩阵,则
阶矩阵,则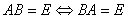
命题:初等矩阵都可逆,且

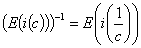
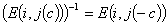
命题:准对角矩阵
 可逆
可逆 每个
每个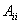 都可逆,记
都可逆,记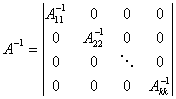
伴随矩阵的基本性质:
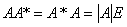
当 可逆时,
可逆时, 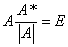 得
得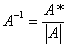 , (求逆矩阵的伴随矩阵法)
, (求逆矩阵的伴随矩阵法)
且得: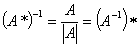
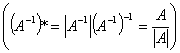
伴随矩阵的其他性质
①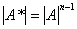 ,
, 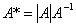
②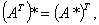
③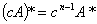 ,
,
④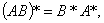
⑤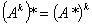 ,
,
⑥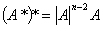 。
。 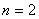 时,
时, 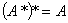
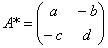
关于矩阵右上肩记号: ,
,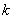 ,
,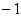 ,*
,*
i) 任何两个的次序可交换,
如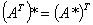 ,
,
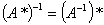 等
等
ii) 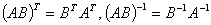 ,
,
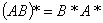
但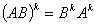 不一定成立!
不一定成立!
线性表示
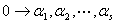
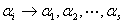
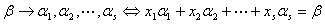 有解
有解
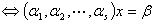 有解
有解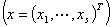
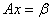 有解,即
有解,即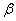 可用A的列向量组表示
可用A的列向量组表示
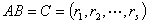 ,
,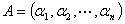 ,
,
则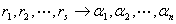 。
。
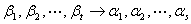 ,
,
则存在矩阵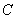 ,使得
,使得
线性表示关系有传递性 当 ,
,
则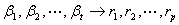 。
。
等价关系:如果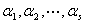 与
与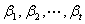 互相可表示
互相可表示 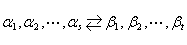
记作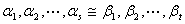 。
。
线性相关
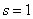 ,单个向量
,单个向量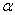 ,
,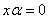
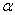 相关
相关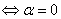
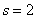 ,
,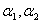 相关
相关 对应分量成比例
对应分量成比例 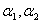 相关
相关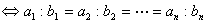
①向量个数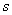 =维数
=维数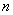 ,则
,则 线性相(无)关
线性相(无)关
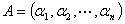 ,
,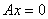 有非零解
有非零解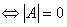
如果 ,则
,则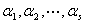 一定相关
一定相关
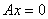 的方程个数
的方程个数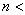 未知数个数
未知数个数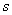
②如果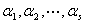 无关,则它的每一个部分组都无关
无关,则它的每一个部分组都无关
③如果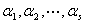 无关,而
无关,而 相关,则
相关,则
证明:设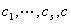 不全为0,使得
不全为0,使得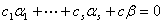
则其中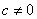 ,否则
,否则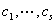 不全为0,
不全为0,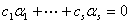 ,与条件
,与条件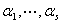 无关矛盾。于是
无关矛盾。于是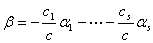 。
。
④当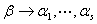 时,表示方式唯一
时,表示方式唯一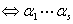 无关
无关
(表示方式不唯一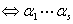 相关)
相关)
⑤若 ,并且
,并且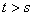 ,则
,则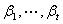 一定线性相关。
一定线性相关。
证明:记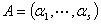 ,
,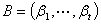 ,
,
则存在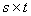 矩阵
矩阵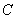 ,使得
,使得 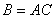 。
。
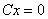 有
有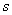 个方程,
个方程,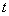 个未知数,
个未知数,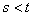 ,有非零解
,有非零解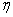 ,
,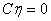 。
。
则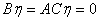 ,即
,即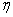 也是
也是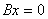 的非零解,从而
的非零解,从而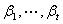 线性相关。
线性相关。
各性质的逆否形式
①如果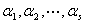 无关,则
无关,则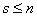 。
。
②如果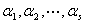 有相关的部分组,则它自己一定也相关。
有相关的部分组,则它自己一定也相关。
③如果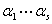 无关,而
无关,而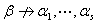 ,则
,则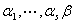 无关。
无关。
⑤如果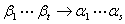 ,
,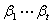 无关,则
无关,则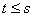 。
。
推论:若两个无关向量组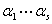 与
与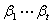 等价,则
等价,则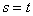 。
。
极大无关组
一个线性无关部分组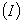 ,若
,若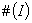 等于秩
等于秩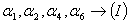 ,
,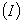 就一定是极大无关组
就一定是极大无关组
①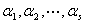 无关
无关
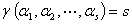
②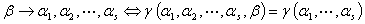
另一种说法: 取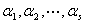 的一个极大无关组
的一个极大无关组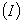
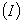 也是
也是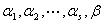 的极大无关组
的极大无关组
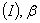 相关。
相关。
证明: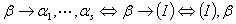 相关。
相关。
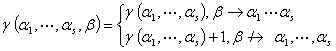
③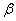 可用
可用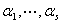 唯一表示
唯一表示
④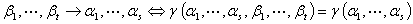
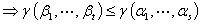
⑤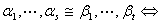

矩阵的秩的简单性质
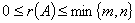

 行满秩:
行满秩: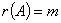
 列满秩:
列满秩: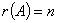
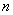 阶矩阵
阶矩阵 满秩:
满秩: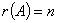
 满秩
满秩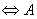 的行(列)向量组线性无关
的行(列)向量组线性无关
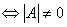
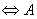 可逆
可逆
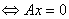 只有零解,
只有零解,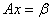 唯一解。
唯一解。
矩阵在运算中秩的变化
初等变换保持矩阵的秩
①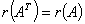
②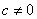 时,
时,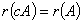
③
④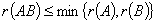
⑤ 可逆时,
可逆时,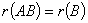
弱化条件:如果 列满秩,则
列满秩,则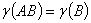
证:下面证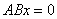 与
与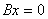 同解。
同解。
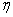 是
是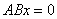 的解
的解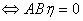
 是
是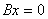 的解
的解
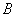 可逆时,
可逆时,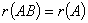
⑥若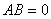 ,则
,则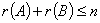 (
( 的列数,
的列数,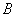 的行数)
的行数)
⑦ 列满秩时
列满秩时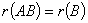
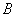 行满秩时
行满秩时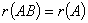
⑧
解的性质
1.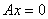 的解的性质。
的解的性质。
如果 是一组解,则它们的任意线性组合
是一组解,则它们的任意线性组合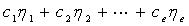 一定也是解。
一定也是解。
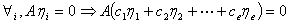
2.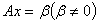
①如果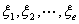 是
是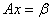 的一组解,则
的一组解,则
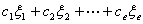 也是
也是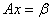 的解
的解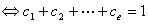
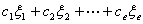 是
是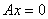 的解
的解
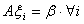
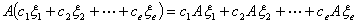

特别的: 当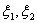 是
是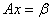 的两个解时,
的两个解时,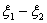 是
是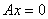 的解
的解
②如果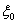 是
是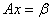 的解,则
的解,则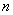 维向量
维向量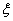 也是
也是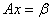 的解
的解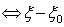 是
是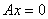 的解。
的解。
解的情况判别
方程: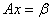 ,即
,即
有解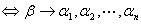
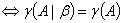

无解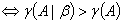 唯一解
唯一解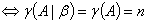 无穷多解
无穷多解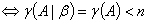
方程个数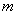 :
:
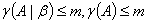
①当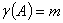 时,
时,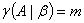 ,有解②当
,有解②当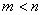 时,
时,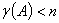 ,不会是唯一解
,不会是唯一解
对于齐次线性方程组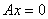 ,
,
只有零解 (即
(即 列满秩)(有非零解
列满秩)(有非零解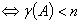 )
)
特征值特征向量
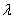 是
是 的特征值
的特征值 是
是 的特征多项式
的特征多项式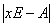 的根。
的根。
两种特殊情形:
(1) 是上(下)三角矩阵,对角矩阵时,特征值即对角线上的元素。
是上(下)三角矩阵,对角矩阵时,特征值即对角线上的元素。
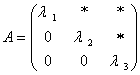
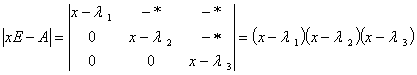
(2)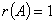 时:
时: 的特征值为
的特征值为
特征值的性质
命题: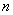 阶矩阵
阶矩阵 的特征值
的特征值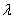 的重数
的重数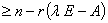
命题:设 的特征值为
的特征值为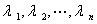 ,则
,则
①
②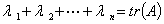
命题:设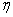 是
是 的特征向量,特征值为
的特征向量,特征值为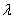 ,即
,即 ,则
,则
①对于 的每个多项式
的每个多项式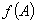 ,
,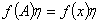
②当 可逆时,
可逆时,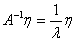 ,
,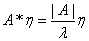
命题:设 的特征值为
的特征值为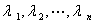 ,则
,则
①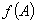 的特征值为
的特征值为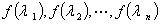
② 可逆时,
可逆时,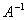 的特征值为
的特征值为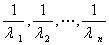
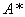 的特征值为
的特征值为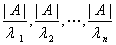
③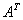 的特征值也是
的特征值也是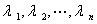
特征值的应用
①求行列式
②判别可逆性
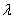 是
是 的特征值
的特征值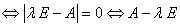 不可逆
不可逆
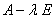 可逆
可逆 不是
不是 的特征值。
的特征值。
当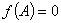 时,如果
时,如果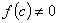 ,则
,则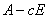 可逆
可逆
若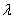 是
是 的特征值,则
的特征值,则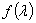 是
是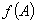 的特征值
的特征值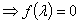 。
。
 不是
不是 的特征值
的特征值 可逆。
可逆。
n阶矩阵的相似关系
当 时,
时,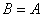 ,而
,而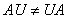 时,
时,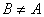 。
。
相似关系有i)对称性: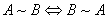
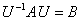 ,则
,则
ii)有传递性: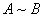 ,
, ,则
,则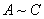
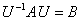 ,
,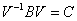 ,则
,则
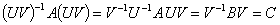
命题 当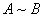 时,
时, 和
和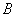 有许多相同的性质
有许多相同的性质
①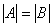
②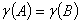
③ ,
,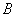 的特征多项式相同,从而特征值完全一致。
的特征多项式相同,从而特征值完全一致。
 与
与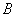 的特征向量的关系:
的特征向量的关系: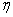 是
是 的属于
的属于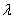 的特征向量
的特征向量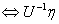 是
是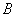 的属于
的属于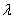 的特征向量。
的特征向量。

正定二次型与正定矩阵性质与判别
可逆线性变换替换保持正定性
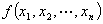 变为
变为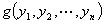 ,则它们同时正定或同时不正定
,则它们同时正定或同时不正定
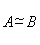 ,则
,则 ,
,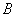 同时正定,同时不正定。
同时正定,同时不正定。
例如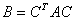 。如果
。如果 正定,则对每个
正定,则对每个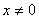
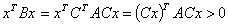
(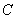 可逆,
可逆,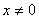 ,
,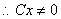 !)
!)
我们给出关于正定的以下性质
 正定
正定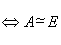
 存在实可逆矩阵
存在实可逆矩阵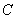 ,
,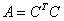 。
。
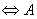 的正惯性指数
的正惯性指数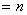 。
。
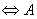 的特征值全大于
的特征值全大于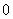 。
。
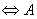 的每个顺序主子式全大于
的每个顺序主子式全大于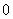 。
。
判断 正定的三种方法:
正定的三种方法:
①顺序主子式法。②特征值法。③定义法。
基本概念
对称矩阵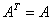 。
。
反对称矩阵 。
。
简单阶梯形矩阵:台角位置的元素都为1 ,台角正上方的元素都为0。
如果 是一个
是一个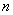 阶矩阵,
阶矩阵, 是阶梯形矩阵
是阶梯形矩阵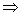
 是上三角矩阵,反之不一定
是上三角矩阵,反之不一定
矩阵消元法:(解的情况)
①写出增广矩阵 ,用初等行变换化
,用初等行变换化 为阶梯形矩阵
为阶梯形矩阵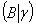 。
。
②用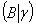 判别解的情况。
判别解的情况。
i)如果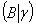 最下面的非零行为
最下面的非零行为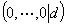 ,则无解,否则有解。
,则无解,否则有解。
ii)如果有解,记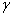 是
是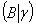 的非零行数,则
的非零行数,则
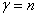 时唯一解。
时唯一解。
 时无穷多解。
时无穷多解。
iii)唯一解求解的方法(初等变换法)
去掉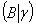 的零行,得
的零行,得 ,它是
,它是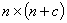 矩阵,
矩阵,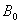 是
是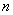 阶梯形矩阵,从而是上三角矩阵。
阶梯形矩阵,从而是上三角矩阵。
则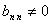
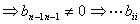 都不为
都不为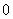 。
。
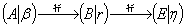
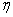 就是解。
就是解。
一个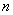 阶行列式
阶行列式 的值:
的值:
①是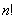 项的代数和
项的代数和
②每一项是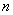 个元素的乘积,它们共有
个元素的乘积,它们共有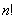 项
项 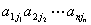 其中
其中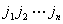 是
是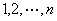 的一个全排列。
的一个全排列。
③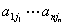 前面乘的应为
前面乘的应为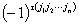
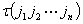 的逆序数
的逆序数
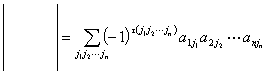
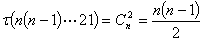
代数余子式
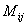 为
为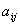 的余子式。
的余子式。
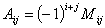
定理:一个行列式的值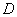 等于它的某一行(列),各元素与各自代数余子式乘积之和。
等于它的某一行(列),各元素与各自代数余子式乘积之和。
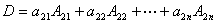
一行(列)的元素乘上另一行(列)的相应元素代数余子式之和为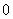 。
。
范德蒙行列式
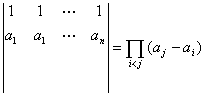
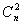 个
个
乘法相关
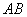 的
的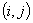 位元素是
位元素是 的第
的第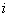 行和
行和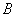 的第
的第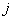 列对应元素乘积之和。
列对应元素乘积之和。

乘积矩阵的列向量与行向量
(1)设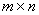 矩阵
矩阵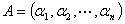 ,
,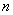 维列向量
维列向量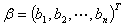 ,则
,则
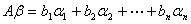
矩阵乘法应用于方程组
方程组的矩阵形式
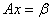 ,
,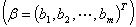
方程组的向量形式

(2)设 ,
,
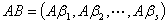
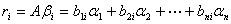
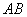 的第
的第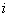 个列向量是
个列向量是 的列向量组的线性组合,组合系数是
的列向量组的线性组合,组合系数是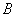 的第
的第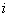 个列向量的各分量。
个列向量的各分量。
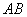 的第
的第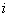 个行向量是
个行向量是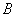 的行向量组的线性组合,组合系数是
的行向量组的线性组合,组合系数是 的第
的第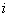 个行向量的各分量。
个行向量的各分量。
矩阵分解
当矩阵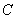 的每个列向量都是
的每个列向量都是 的列向量的线性组合时,可把
的列向量的线性组合时,可把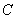 分解为
分解为 与一个矩阵
与一个矩阵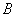 的乘积
的乘积
特别的在有关对角矩阵的乘法中的若干问题

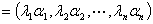
对角矩阵从右侧乘一矩阵 ,即用对角线上的元素依次乘
,即用对角线上的元素依次乘 的各列向量
的各列向量
对角矩阵从左侧乘一矩阵 ,即用对角线上的元素依次乘
,即用对角线上的元素依次乘 的各行向量
的各行向量
于是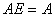 ,
,
 ,
,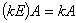
两个对角矩阵相乘只须把对角线上对应元素相乘
对角矩阵的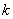 次方幂只须把每个对角线上元素作
次方幂只须把每个对角线上元素作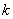 次方幂
次方幂
对一个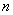 阶矩阵
阶矩阵 ,规定
,规定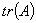 为
为 的对角线上元素之和称为
的对角线上元素之和称为 的迹数。
的迹数。
于是 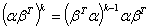
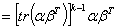
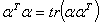
其他形式方阵的高次幂也有规律
例如: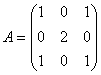
初等矩阵及其在乘法中的作用
(1)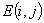 :交换
:交换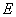 的第
的第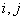 两行或交换
两行或交换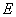 的第
的第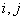 两列
两列
(2)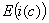 :用数
:用数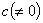 乘
乘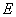 的第
的第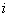 行或第
行或第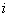 列
列
(3)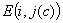 :把
:把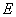 的第
的第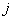 行的
行的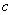 倍加到第
倍加到第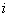 行上,或把
行上,或把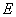 的第
的第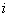 列的
列的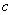 倍加到第
倍加到第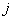 列上。
列上。
初等矩阵从左(右)侧乘一个矩阵 等同于对
等同于对 作一次相当的初等行(列)变换
作一次相当的初等行(列)变换
乘法的分块法则
一般法则:在计算两个矩阵 和
和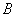 的乘积时,可以先把
的乘积时,可以先把 和
和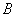 用纵横线分割成若干小矩阵来进行,要求
用纵横线分割成若干小矩阵来进行,要求 的纵向分割与
的纵向分割与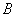 的横向分割一致。
的横向分割一致。

两种常用的情况
(1)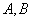 都分成4块
都分成4块
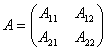 ,
,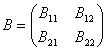
其中 的列数和
的列数和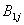 的行数相等,
的行数相等,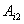 的列数和
的列数和 的行数相关。
的行数相关。
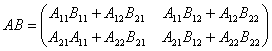
(2)准对角矩阵

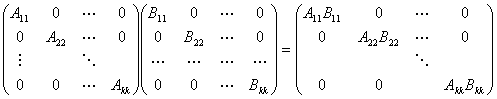
矩阵方程与可逆矩阵
两类基本的矩阵方程 (都需求 是方阵,且
是方阵,且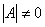 )
)
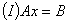
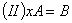
(I)的解法:
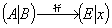
(II)的解法,先化为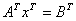 。
。
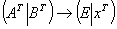 。
。
通过逆求解: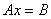 ,
,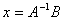
可逆矩阵及其逆矩阵
定义:设 是
是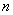 阶矩阵,如果存在
阶矩阵,如果存在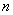 阶矩阵
阶矩阵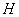 ,使得
,使得 ,且
,且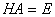 ,则称
,则称 是可逆矩阵,称
是可逆矩阵,称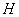 是
是 的逆矩阵,证作
的逆矩阵,证作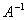 。
。
定理: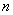 阶矩阵
阶矩阵 可逆
可逆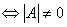
求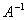 的方程(初等变换法)
的方程(初等变换法)
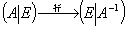
伴随矩阵
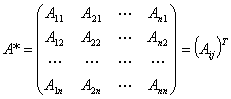
线性表示
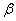 可以用
可以用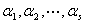 线性表示,即
线性表示,即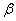 可以表示为
可以表示为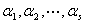 的线性组合,
的线性组合,
也就是存在 使得
使得 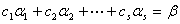
记号:
线性相关性
线性相关:存在向量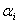 可用其它向量
可用其它向量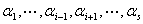 线性表示。
线性表示。
线性无关:每个向量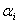 都不能用其它向量线性表示
都不能用其它向量线性表示
定义:如果存在不全为 的
的 ,使得
,使得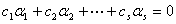 则称
则称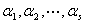 线性相关,否则称
线性相关,否则称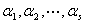 线性无关。
线性无关。
即: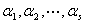 线性相(无)关
线性相(无)关 有(无)非零解
有(无)非零解
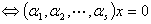 有(无)非零解
有(无)非零解
极大无关组和秩
定义: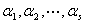 的一个部分组
的一个部分组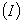 称为它的一个极大无关组,如果满足:
称为它的一个极大无关组,如果满足:
i)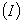 线性无关。 ii)
线性无关。 ii)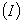 再扩大就相关。
再扩大就相关。
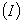
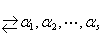
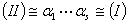
定义:规定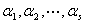 的秩
的秩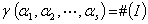 。
。
如果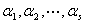 每个元素都是零向量,则规定其秩为
每个元素都是零向量,则规定其秩为 。
。
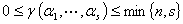
有相同线性关系的向量组
定义:两个向量若有相同个数的向量: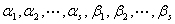 ,并且向量方程
,并且向量方程
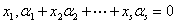 与
与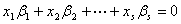 同解,则称它们有相同的线性关系。
同解,则称它们有相同的线性关系。
①对应的部分组有一致的相关性。
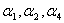 的对应部分组
的对应部分组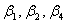 ,
,
若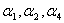 相关,有不全为
相关,有不全为 的
的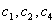 使得
使得
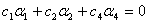 ,
,
即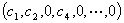 是
是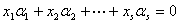 的解,
的解,
从而也是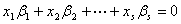 的解,则有
的解,则有
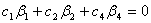 ,
, 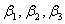 也相关。
也相关。
②极大无关组相对应,从而秩相等。 ③有一致的内在线表示关系。
设: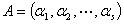 ,
,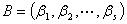 ,则
,则
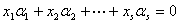 即
即 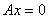 ,
,
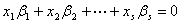 即
即 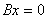 。
。
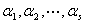 与
与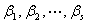 有相同的线性关系即
有相同的线性关系即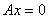 与
与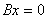 同解。
同解。
反之,当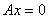 与
与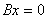 同解时,
同解时, 和
和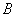 的列向量组有相同的线性关系。
的列向量组有相同的线性关系。
矩阵的秩
定理:矩阵 的行向量组的秩=列向量组的秩
的行向量组的秩=列向量组的秩
规定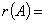 行(列)向量组的秩。
行(列)向量组的秩。
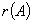 的计算:用初等变换化
的计算:用初等变换化 为阶梯形矩阵
为阶梯形矩阵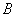 ,则
,则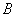 的非零行数即
的非零行数即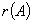 。
。
命题: 的非零子式阶数的最大值。
的非零子式阶数的最大值。
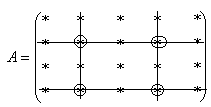
方程组的表达形式
1.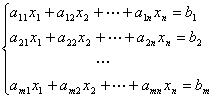
2.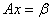
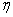 是解
是解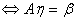
3. 有解
有解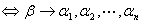
基础解系和通解
1.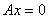 有非零解时的基础解系
有非零解时的基础解系
 是
是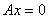 的基础解系的条件:
的基础解系的条件:
①每个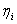 都是
都是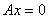 的解②
的解② 线性无关③
线性无关③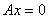 的每个解
的每个解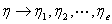 ③/
③/ 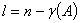
通解
①如果 是
是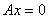 的一个基础解系,则
的一个基础解系,则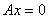 的通解为
的通解为
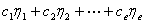 ,
,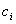 任意
任意
②如果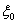 是
是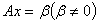 的一个解,
的一个解, 是
是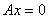 的基础解系,则
的基础解系,则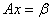 的通解为
的通解为
 ,
,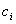 任意
任意
特征向量与特征值
定义:如果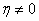 ,并且
,并且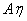 与
与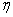 线性相关,则称
线性相关,则称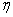 是
是 的一个特征向量。此时,有数
的一个特征向量。此时,有数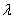 ,使得
,使得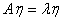 ,称
,称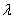 为
为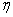 的特征值。
的特征值。
设 是数量矩阵
是数量矩阵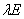 ,则对每个
,则对每个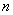 维列向量
维列向量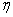 ,
,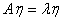 ,于是,任何非零列向量都是
,于是,任何非零列向量都是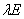 的特征向量,特征值都是
的特征向量,特征值都是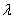 。
。
①特征值有限特征向量无穷多
若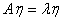 ,
,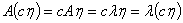
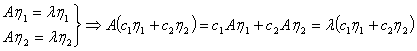
②每个特征向量有唯一特征值,而有许多特征向量有相同的特征值。
③计算时先求特征值,后求特征向量。
特征向量与特征值计算

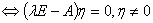
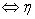 是
是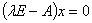 的非零解
的非零解
命题:①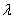 是
是 的特征值
的特征值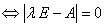
②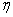 是属于
是属于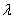 的特征向量
的特征向量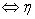 是
是 的非零解
的非零解
称多项式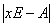 为
为 的特征多项式。
的特征多项式。
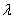 是
是 的特征值
的特征值 是
是 的特征多项式
的特征多项式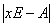 的根。
的根。
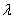 的重数:
的重数: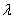 作为
作为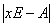 的根的重数。
的根的重数。
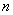 阶矩阵
阶矩阵 的特征值有
的特征值有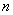 个:
个: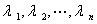 ,可能其中有的不是实数,有的是多重的。
,可能其中有的不是实数,有的是多重的。
计算步骤:
①求出特征多项式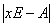 。
。
②求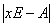 的根,得特征值。
的根,得特征值。
③对每个特征值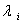 ,求
,求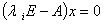 的非零解,得属于
的非零解,得属于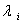 的特征向量。
的特征向量。
n阶矩阵的相似关系
设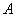 ,
, 是两个
是两个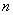 阶矩阵。如果存在
阶矩阵。如果存在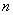 阶可逆矩阵
阶可逆矩阵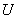 ,使得
,使得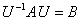 ,则称
,则称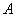 与
与 相似,记作
相似,记作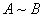 。
。
n阶矩阵的对角化
基本定理 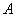 可对角化
可对角化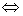
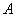 有
有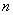 个线性无关的特征向量。
个线性无关的特征向量。
设可逆矩阵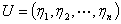 ,则
,则
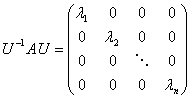
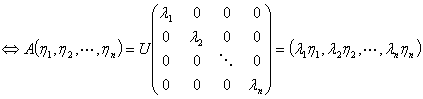
 ,
,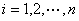
判别法则
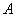 可对角化
可对角化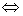 对于
对于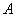 的每个特征值
的每个特征值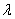 ,
,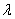 的重数
的重数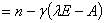 。
。
计算:对每个特征值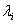 ,求出
,求出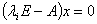 的一个基础解系,把它们合在一起,得到
的一个基础解系,把它们合在一起,得到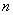 个线性无关的特征向量,
个线性无关的特征向量,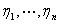 。令
。令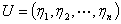 ,则
,则
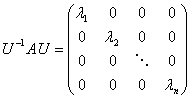 ,其中
,其中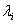 为
为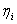 的特征值。
的特征值。
二次型(实二次型)
二次型及其矩阵
一个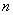 元二次型的一般形式为
元二次型的一般形式为
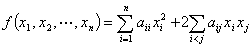
只有平方项的二次型称为标准二次型。
形如: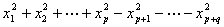 的
的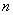 元二次型称为规范二次型。
元二次型称为规范二次型。
对每个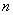 阶实矩阵
阶实矩阵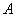 ,记
,记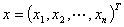 ,则
,则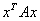 是一个二次型。
是一个二次型。
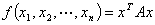
称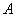 的秩
的秩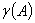 为这个二次型的秩。 标准二次型的矩阵是对角矩阵。 规范二次型的矩阵是规范对角矩阵。
为这个二次型的秩。 标准二次型的矩阵是对角矩阵。 规范二次型的矩阵是规范对角矩阵。
可逆线性变量替换
设有一个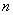 元二次型
元二次型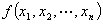 ,引进新的一组变量
,引进新的一组变量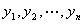 ,并把
,并把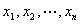 用它们表示。
用它们表示。
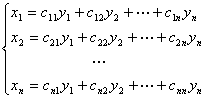 (并要求矩阵
(并要求矩阵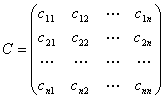 是可逆矩阵)
是可逆矩阵)
代入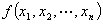 ,得到
,得到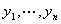 的一个二次型
的一个二次型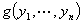 这样的操作称为对
这样的操作称为对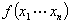 作了一次可逆线性变量替换。
作了一次可逆线性变量替换。
设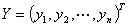 ,则上面的变换式可写成
,则上面的变换式可写成 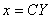
则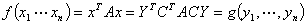
于是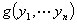 的矩阵为
的矩阵为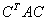
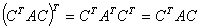
实对称矩阵的合同
两个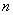 阶实对称矩阵
阶实对称矩阵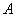 和
和 ,如果存在
,如果存在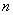 阶实可逆矩阵
阶实可逆矩阵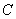 ,值得
,值得 。称
。称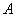 与
与 合同,记作
合同,记作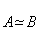 。
。
命题:二次型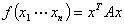 可用可逆线性变换替换化为
可用可逆线性变换替换化为
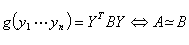
二次型的标准化和规范化
1.每个二次型都可以用可逆线性变量替换化为标准二次型和规范二次型。
也就是每个实对称矩阵都会同于对角矩阵和规范对角矩阵。
设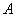 是一个实对称矩阵,则存在正交矩阵
是一个实对称矩阵,则存在正交矩阵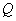 ,使得
,使得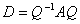 是对角矩阵。
是对角矩阵。
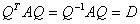
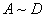 ,
,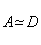
2.标准化和规范化的方法
①正交变换法
② 配方法
3.惯性定理与惯性指数
定理:一个二次型用可逆线性变换替换化出的标准形的各个平方项的系数中,大于0的个数和小于0的个数是由原二次型所决定的,分别称为原二次型的正、负惯性指数。
一个二次型化出的规范二次型在形式上是唯一的,也即相应的规范对角矩阵是唯一的。
用矩阵的语言来说:一个实对称矩阵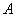 合同于唯一规范对角矩阵。
合同于唯一规范对角矩阵。
定理:二次型的正、负惯性指数在可逆线性变量替换下不变;两个二次型可互相转化的充要条件是它们的正、负惯性指数相等。
实对称矩阵的正(负)惯性指数就等于正(负)特征值的个数。
正定二次型与正定矩阵
定义:一个二次型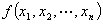 称为正定二次型,如果当
称为正定二次型,如果当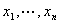 不全为0时,
不全为0时,
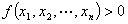 。
。
例如,标准二次型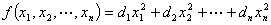 正定
正定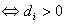 ,
,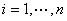
(必要性“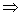 ”,取
”,取 ,
,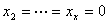 ,此时
,此时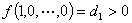 同样可证每个
同样可证每个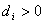 )
)
实对称矩阵正定即二次型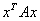 正定,也就是:当
正定,也就是:当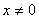 时,
时,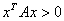 。
。
例如实对角矩阵 正定
正定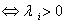 ,
,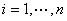
定义:设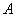 是一个
是一个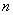 阶矩阵,记
阶矩阵,记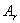 是
是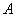 的西北角的
的西北角的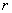 阶小方阵,称
阶小方阵,称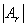 为
为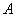 的第
的第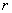 个顺序主子式(或
个顺序主子式(或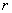 阶顺序主子式)。
阶顺序主子式)。
