线性代数公式总结
行列式
1. 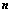 行列式共有
行列式共有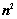 个元素,展开后有
个元素,展开后有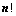 项,可分解为
项,可分解为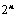 行列式;
行列式;
2. 代数余子式的性质:
①、 和
和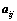 的大小无关;
的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0;
③、某行(列)的元素乘以该行(列)元素的代数余子式为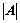 ;
;
3. 代数余子式和余子式的关系:
4. 设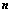 行列式
行列式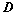 :
:
将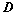 上、下翻转或左右翻转,所得行列式为
上、下翻转或左右翻转,所得行列式为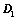 ,则
,则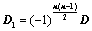 ;
;
将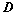 顺时针或逆时针旋转
顺时针或逆时针旋转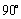 ,所得行列式为
,所得行列式为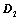 ,则
,则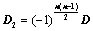 ;
;
将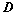 主对角线翻转后(转置),所得行列式为
主对角线翻转后(转置),所得行列式为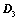 ,则
,则 ;
;
将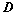 主副角线翻转后,所得行列式为
主副角线翻转后,所得行列式为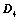 ,则
,则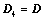 ;
;
5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
②、副对角行列式:副对角元素的乘积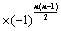 ;
;
③、上、下三角行列式(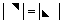 ):主对角元素的乘积;
):主对角元素的乘积;
④、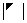 和
和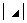 :副对角元素的乘积
:副对角元素的乘积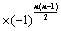 ;
;
⑤、拉普拉斯展开式: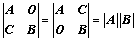 、
、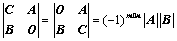
⑥、范德蒙行列式:大指标减小指标的连乘积;
⑦、特征值;
6. 对于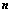 阶行列式
阶行列式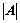 ,恒有:
,恒有: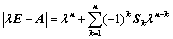 ,其中
,其中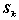 为
为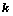 阶主子式;
阶主子式;
7. 证明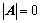 的方法:
的方法:
①、 ;
;
②、反证法;
③、构造齐次方程组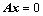 ,证明其有非零解;
,证明其有非零解;
④、利用秩,证明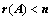 ;
;
⑤、证明0是其特征值;
…… …… 余下全文

 矩阵
矩阵 ,总可经过初等行变换化为行阶梯矩阵或行最简形矩阵,总可经过初等变换化为标准形,其标准形是唯一确定的:
,总可经过初等行变换化为行阶梯矩阵或行最简形矩阵,总可经过初等变换化为标准形,其标准形是唯一确定的: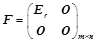 ;对于同型矩阵
;对于同型矩阵 ,若
,若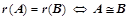 ;
;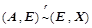 ,则
,则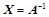 ;
; 做初等行变换,如果:
做初等行变换,如果: ;则
;则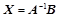 为矩阵方程
为矩阵方程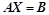 的解;
的解;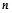 个未知数
个未知数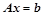 ,如果
,如果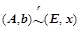 ,则
,则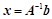 ;
;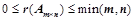 ;②、
;②、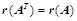 ;③、若
;③、若 ,则
,则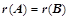 ;
;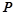 、
、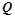 可逆,则
可逆,则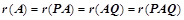 (可逆矩阵不影响矩阵的秩);
(可逆矩阵不影响矩阵的秩);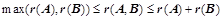 ;⑥、
;⑥、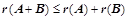 ;⑦、
;⑦、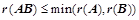 ;
;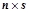 矩阵,且
矩阵,且 ,则:
,则: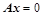 解;Ⅱ、
解;Ⅱ、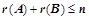
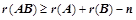 ;
;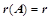 ,
,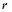 阶子式不为0,
阶子式不为0,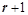 阶子式全部为0;(两句话)
阶子式全部为0;(两句话)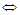
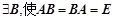
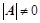 (是非奇异矩阵)
(是非奇异矩阵)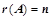 (是满秩矩阵)
(是满秩矩阵)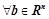 ,
,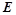 等价
等价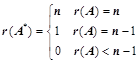 ;②、伴随矩阵的特征值:
;②、伴随矩阵的特征值: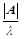 ;③、
;③、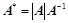 、
、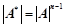
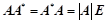 无条件恒成立;
无条件恒成立; 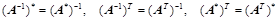
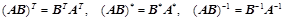
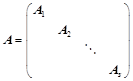 ,则:Ⅰ、
,则:Ⅰ、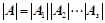 ;Ⅱ、
;Ⅱ、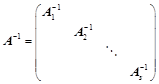 ;
; ;(主对角分块)③、
;(主对角分块)③、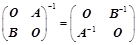 ;(副对角分块)
;(副对角分块)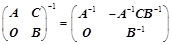 ;⑤、
;⑤、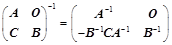 ;(拉普拉斯)
;(拉普拉斯)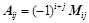
 行列式共有
行列式共有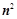 个元素,展开后有
个元素,展开后有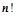 项,可分解为
项,可分解为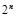 行列式;
行列式;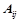 和
和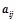 的大小无关;
的大小无关;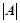 ;
;
 :
: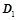 ,则
,则 ;
;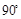 ,所得行列式为
,所得行列式为 ,则
,则 ;
;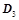 ,则
,则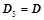 ;
;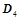 ,则
,则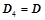 ;
;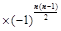 ;
;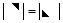 ):主对角元素的乘积;
):主对角元素的乘积;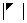 和
和 :副对角元素的乘积
:副对角元素的乘积 、
、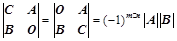
 ,其中
,其中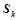 为
为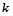 阶主子式;
阶主子式; 的方法:
的方法: ;
;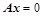 ,证明其有非零解;
,证明其有非零解;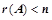 ;
; 是
是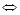
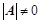 (是非奇异矩阵);
(是非奇异矩阵); (是满秩矩阵)
(是满秩矩阵) ,
,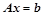 总有唯一解;
总有唯一解; 等价;
等价;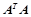 是正定矩阵;
是正定矩阵;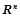 的一组基;
的一组基;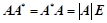 无条件恒成立;
无条件恒成立;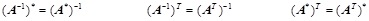
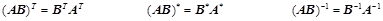
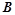 可逆:
可逆: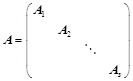 ,则:
,则: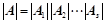 ;
;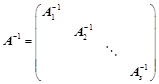 ;
;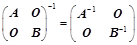 ;(主对角分块)
;(主对角分块)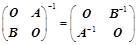 ;(副对角分块)
;(副对角分块)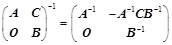 ;(拉普拉斯)
;(拉普拉斯)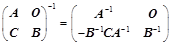 ;(拉普拉斯)
;(拉普拉斯) 矩阵
矩阵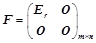 ;
;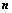 行列式共有
行列式共有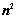 个元素,展开后有
个元素,展开后有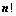 项,可分解为
项,可分解为 行列式;
行列式;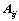 和
和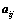 的大小无关;
的大小无关; ;
;
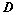 :
: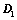 ,则
,则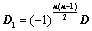 ;
; ,所得行列式为
,所得行列式为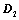 ,则
,则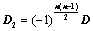 ;
;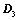 ,则
,则 ;
;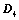 ,则
,则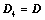 ;
;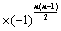 ;
; ):主对角元素的乘积;
):主对角元素的乘积;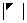 和
和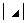 :副对角元素的乘积
:副对角元素的乘积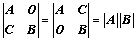 、
、
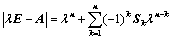 ,其中
,其中 为
为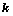 阶主子式;
阶主子式; 的方法:
的方法: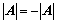 ;
;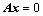 ,证明其有非零解;
,证明其有非零解;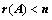 ;
;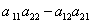 称为
称为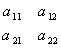 所确定的二阶行列式,并记作
所确定的二阶行列式,并记作 ,
,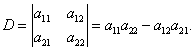 结果为一个数。(课本P1)
结果为一个数。(课本P1) 称为由数表
称为由数表 所确定的三阶行列式,记作
所确定的三阶行列式,记作 。
。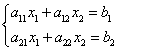
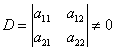
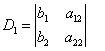
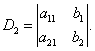
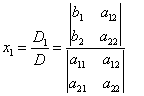 ,
,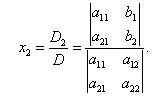 (课本P2)
(课本P2)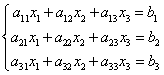 ,
,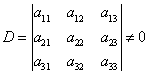 ,
,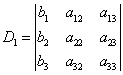 ,
,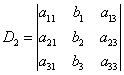 ,
,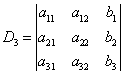 ,
,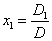 ,
,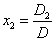 ,
,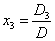 。(课本上没有)
。(课本上没有)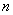 个不同的元素排成一列,叫做这
个不同的元素排成一列,叫做这 前面比它大的数码之和即分别算出
前面比它大的数码之和即分别算出 等于所有取自不同行、不同列的n个元素的乘积
等于所有取自不同行、不同列的n个元素的乘积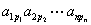 的代数和,其中p1 p2 … pn是1, 2, … ,n的一个排列,每一项的符号由其逆序数决定。
的代数和,其中p1 p2 … pn是1, 2, … ,n的一个排列,每一项的符号由其逆序数决定。 也可简记为
也可简记为 ,其中
,其中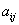 为行列式D的(i,j元)。(课本P6)
为行列式D的(i,j元)。(课本P6)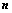 行列式共有
行列式共有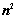 个元素,展开后有
个元素,展开后有 项,可分解为
项,可分解为 行列式;
行列式;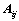 和
和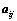 的大小无关;
的大小无关;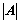 ;
;
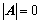 的方法:
的方法: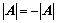 ;
; ,证明其有非零解;
,证明其有非零解;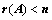 ;
;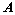 是
是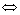
 (是非奇异矩阵);
(是非奇异矩阵);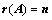 (是满秩矩阵)
(是满秩矩阵)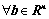 ,
,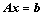 总有唯一解;
总有唯一解;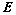 等价;
等价;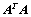 是正定矩阵;
是正定矩阵;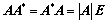 无条件恒成立;
无条件恒成立;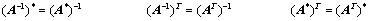
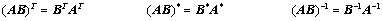
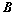 可逆:
可逆: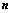 行列式共有
行列式共有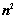 个元素,展开后有
个元素,展开后有 项,可分解为
项,可分解为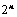 行列式;
行列式;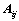 和
和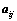 的大小无关;
的大小无关;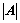 ;
;
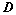 :
: ,则
,则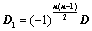 ;
; ,所得行列式为
,所得行列式为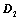 ,则
,则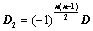 ;
;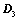 ,则
,则 ;
;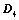 ,则
,则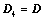 ;
; ;
; ):主对角元素的乘积;
):主对角元素的乘积;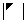 和
和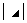 :副对角元素的乘积
:副对角元素的乘积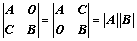 、
、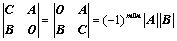
 ,其中
,其中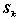 为
为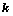 阶主子式;
阶主子式;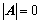 的方法:
的方法: ;
;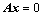 ,证明其有非零解;
,证明其有非零解; ;
;