泛函分析课程论文
泛函分析课程的知识体系总结各个知识点之间的区别和联系
(一)、度量空间和赋范线性空间
第一节 度量空间的进一步例子
1.距离空间的定义:设X是非空集合,若存在一个映射d:X×X→R,使得 x,y,z
x,y,z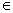 X,下列距离公理成立:
X,下列距离公理成立:
(1)非负性:d(x,y)≥0,d(x,y)=0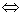 x=y;
x=y;
(2)对称性:d(x,y)=d(y,x);
(3)三角不等式:d(x,y)≤d(x,z)+d(z,y);
则称d(x,y)为x与y的距离,X为以d为距离的距离空间,记作(X,d)
2.几类空间
例1 离散的度量空间
例2 序列空间S
例3 有界函数空间B(A)
例4 可测函数空M(X)
例5 C[a,b]空间 即连续函数空间
例6 l2
第二节 度量空间中的极限,稠密集,可分空间
1. 开球
定义 设(X,d)为度量空间,d是距离,定义
U(x0, 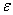 )={x ∈X | d(x, x0) <
)={x ∈X | d(x, x0) <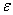 }
}
为x0的以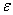 为半径的开球,亦称为x0的
为半径的开球,亦称为x0的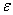 一领域.
一领域.
2. 极限
定义 若{xn } X,
X, 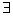 x
x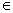 X, s.t.
X, s.t. 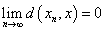 则称
则称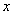 是点列{xn }的极限.
是点列{xn }的极限.
3. 有界集
定义 若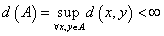 ,则称A有界
,则称A有界
4. 稠密集
定义 设X是度量空间,E和M是X中两个子集,令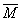 表示M的闭包,如果
表示M的闭包,如果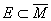 ,那么称集M在集E中稠密,当E=X时称M为X的一个稠密集。
,那么称集M在集E中稠密,当E=X时称M为X的一个稠密集。
5. 可分空间
定义 如果X有一个可数的稠密子集,则称X是可分空间。
第三节 连续映射
1.定义 设X=(X,d),Y=(Y, 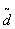 )是两个度量空间,T是X到Y中映射,x0
)是两个度量空间,T是X到Y中映射,x0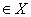 ,如果对于任意给定的正数
,如果对于任意给定的正数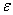 ,存在正数
,存在正数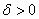 ,使对X中一切满足
,使对X中一切满足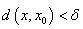 的x,有
的x,有
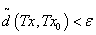 ,
,
则称T在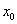 连续.
连续.
2.定理1 设T是度量空间(X,d)到度量空间 中的映射,那么T在
中的映射,那么T在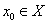 连续的充要条件为当
连续的充要条件为当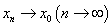 时,必有
时,必有
3.定理2 度量空间X到Y中的映射T是X上连续映射的充要条件为Y中任意开集M的原像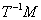 是X中的开集.
是X中的开集.
第四节 柯西(cauchy)点列和完备度量空间
1.定义 设X=(X,d)是度量空间,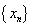 是X中点列,如果对任意给定的正数
是X中点列,如果对任意给定的正数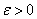 ,存在正整数
,存在正整数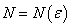 ,使当n,m>N时,必有
,使当n,m>N时,必有
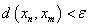 ,
,
则称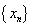 是X中的柯西点列或基本点列。如果度量空间(X,d)中每个柯西点列都在
是X中的柯西点列或基本点列。如果度量空间(X,d)中每个柯西点列都在
(X,d)中收敛,那么称(X,d)是完备的度量空间.
【注意】(1)Q不是完备集
(2)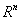 完备
完备
(3)cauchy列不一定收敛,但收敛列一定是cauchy列.
(4)C[a,b]完备
2.定理 完备度量空间X的子空间M是完备空间的充要条件为M是X中的闭子空间.
第五节 度量空间的完备化
1.定义 设(X,d),( 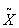 ,
,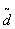 )是两个度量空间,如果存在X到
)是两个度量空间,如果存在X到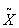 上的保距映射T,即
上的保距映射T,即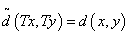 ,则称(X,d)和(
,则称(X,d)和( 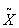 ,
,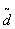 )等距同构,此时T称为X到
)等距同构,此时T称为X到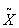 上等距同构映射。
上等距同构映射。
2.定理1(度量空间的完备化定理) 设X=(X,d)是度量空间,那么一定存在一完备度量空间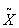 =(
=( 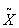 ,
,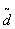 ),使X与
),使X与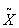 的某个稠密子空间W等距同构,并且
的某个稠密子空间W等距同构,并且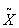 在等距同构意义下是唯一的,即若(
在等距同构意义下是唯一的,即若( 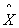 ,
,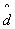 )也是一完备度量空间,且X与
)也是一完备度量空间,且X与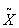 的某个稠密子空间等距同构,则(
的某个稠密子空间等距同构,则( 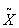 ,
,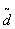 )与(
)与( 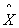 ,
,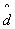 )等距同构。
)等距同构。
3.定理1’ 设X=(X,d)是度量空间,那么存在唯一的完备度量空间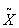 =(
=( 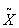 ,
,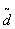 ),使X为
),使X为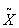 的稠密子空间。
的稠密子空间。
第六节 压缩映射原理及其应用
1.定义 设X是度量空间,T是X到X中的映射,如果存在一个数 ,0<
,0< <1,使得对所有的
<1,使得对所有的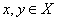 ,
,
 ,
,
则称T是压缩映射。
2.定理1(压缩映射定理)(即Barnach不动点定理) 设X是完备的度量空间,T是X上的压缩映射,那么T有且只有一个不动点(就是说,方程Tx=x,有且只有一个解).
补充定义:若Tx=x,则称x是T的不动点。
x是T的不动点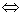 x是方程Tx=x的解。
x是方程Tx=x的解。
3.定理2 设函数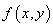 在带状域
在带状域
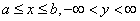
中处处连续,且处处有关于y的偏导数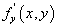 .如果还存在常数m和M满足
.如果还存在常数m和M满足
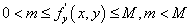 ,
,
则方程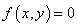 在区间
在区间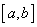 上必有唯一的连续函数
上必有唯一的连续函数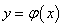 作为解:
作为解:

第七节 线性空间
1.定义1 设X是一非空集合,在X中定义了元素的加法运算和实数(或复数)与X中元素的乘法运算,满足下列条件:
(1)关于加法成为交换群,即对任意x,y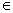 X,存在u
X,存在u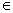 X与之相对应,记为u=x+y,称为x和y的和,满足
X与之相对应,记为u=x+y,称为x和y的和,满足
1)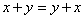 ;
;
2)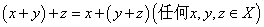 ;
;
3)在X中存在唯一元素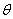 ,使对任何
,使对任何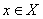 ,成立
,成立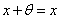 ,称
,称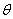 为X中零元素;
为X中零元素;
4)对X中每个元素x,存在唯一元素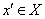 ,使
,使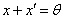 ,称
,称 为
为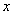 的负元素,记为
的负元素,记为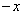 ;
;
(2)对于X中每个元素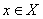 ,及任意实数(或复数)a,存在元素u
,及任意实数(或复数)a,存在元素u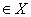 与之对应,记为
与之对应,记为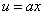 ,称为a与x的数积,满足
,称为a与x的数积,满足
1)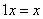 ;
;
2)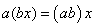 对任意实数(或复数)a和b成立;
对任意实数(或复数)a和b成立;
3)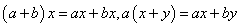 ,
,
则称X按上述加法和数乘运算成为线性空间或向量空间,其中的元素称为向量。如果数积运算只对实数(复数)有意义,则称X是实(复)线性空间。
例1 Rn,对Rn中任意两点x=(ξ1,ξ2,…,ξn ),y=(η1,η2,…,ηn)和任何实(复)数a,定义
x+y=(ξ1 +η1,ξ2 +η2,…,ξn +ηn),
ax=(aξ1 ,aξ2,…,aξn).
容易验证Rn按上述加法和数乘运算成实(复)线性空间.
2.定义2 设x1 ,x2,…,xn 是线性空间X中的向量,如果存在n个不全为零的数α1,α2,…,αn,使
α1 x1 +α2 x2 +…+αnxn =0, (1)
则称x1,x2 ,…,xn 线性相关,否则称为线性无关.
不难看出,x1,x2,…,xn 线性无关的充要条件为,若 ,
,
必有α1 =α2 =…=αn =0.
3.定义3 设M是线性空间X的一个子集,如果M 中任意有限个向量都线性无关,则称M 是X中线性无关子集.设M 和L为X中两个子集,若M 中任何向量与L中任何向量都线性无关,则称M和L线性无关.
4.定义4 设X是线性空间, M 是X中线性无关子集,如果·spanM= X,则称M 的基数为X的维数,记为dim X, M 称为X的一组基.如果M 的基数为有限数,则称X是有限维线性空间,否则称X是无限维线性空间.如果X只含零元素,称X为零维线性空间.
第八节 赋范线性空间和巴拿赫(Banach)空间
1.定义1 设X是实(或复)的线性空间,如果对每个向量x∈X,有一个确定的实数,记为‖x‖与之对应,并且满足:
1°‖x‖≥0,且‖x‖=0等价于x=0;
2°‖αx‖=|α|‖x‖其中α为任意实(复)数;
3°‖x+y‖≤‖x‖+‖y‖,x,y∈X,
则称‖x‖为向量x的范数,称X按范数‖x‖成为赋范线性空间.
2.引理1(H?lder不等式) 设p>1, 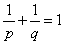 ,
, 那么f(t)g(t)在[a,b]上L可积,并且
那么f(t)g(t)在[a,b]上L可积,并且
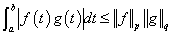
3引理2(Minkowski不等式) 设p≥1,f,g∈Lp[a,b],那么f+g∈Lp[a,b],并且成立不等式
‖f+g‖p ≤‖f‖p +‖g‖p
4.定理1 当p≥1时,Lp[a,b]按(6)中范数‖f‖p 成为赋范线性空间.
5.定理2 Lp [a,b](p≥1)是Banach空间.
6.定理3 设X是n维赋范线性空间,{e1,e2,…,en}是X的一组基,则存在常数M 和M′,使得对一切
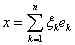
成立
 .
.
7.推论1 设在有限维线性空间上定义了两个范数‖x‖和‖x‖1 ,那么必存在常数M 和
M′,使得
M‖x‖≤‖x‖1 ≤M′‖x‖.
8. 定义2 设(R1,‖x‖1 )和(R2 ,‖x‖2 )是两个赋范线性空间.如果存在从R1 到R2 上的线性映射φ和正数c1 ,c2,使得对一切x∈R1,成立
c1 ‖φx‖2 ≤‖x‖1 ≤c2 ‖φx‖2
则称(R1 ,‖x‖1)和(R2,‖x‖2 )这两个赋范空间是拓扑同构的.
8.推论2 任何有限维赋范空间都和同维数欧氏空间拓扑同构.相同维数的有限维赋范空间彼此拓扑同构.
(二)有界线性算子和连续线性泛函
第一节 有界线性算子和连续线性泛函
定义1 设X和Y是两个同为实(或复)的线性空间,D是X的线性子空间,T为D到Y中的映射,如果对任何x,y∈D,及数α,有
T(x+y)= Tx+ Ty, (1)
T(αx)=αTx, (2)
则称T为D到Y中的线性算子,其中D称为T的定义域,记为D(T),TD称为T的值域,记为R(T),当T取值于实(或复)数域时,就称T为实(或复)线性泛函.
定义2 设X和Y是两个赋范线性空间,T是X的线性子空间D(T)到Y 中的线性算子,如果存在常数c,使对所有x∈D(T),有
‖Tx‖≤c‖x‖, (3)
则称T是D(T)到Y中的有界线性算子,当D(T)= X时,称T为X到Y中的有界线性算子,简称为有界算子.对于不满足条件(3)的算子,称为无界算子.本书主要讨论有界算子.
定理1 设T是赋范线性空间X到赋范线性空间Y中的线性算子,则T为有界算子的充要条件为T是X上连续算子.
定理2 设X是赋范线性空间,f是X上线性泛函,那么f是X上连续泛函的充要条件为f的零空间N(f)是X中的闭子空间
定义3 T为赋范线性空间X的子空间D(T)到赋范线性空
间Y中的线性算子,称
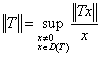 (4)
(4)
为算子T在D(T)上的范数.
引理1 设T是D(T)上有界线性算子,那么
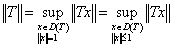 (6)
(6)
Ⅲ. 有界线性算子和连续线性泛函的例子
例6 赋范线性空间X上的相似算子Tx=αx是有界线性算子,且‖T‖=|α|,特别‖IX ‖=1,‖O‖=0.
第二节 有界线性算子空间和共轭空间
Ⅰ. 有界线性算子全体所成空间
定理1 当Y是Banach空间时,B(X→Y)也是Banach空间.
Ⅱ. 共轭空间
定义1 设X是赋范线性空间,令X′表示X上连续线性泛函全体所成的空间,称为X的共轭空间.
定理2 任何赋范线性空间的共轭空间是Banach空间.
定义2 设X和Y是两个赋范线性空间,T是X到Y中的线性算子,并且对所有x∈X,有
‖Tx‖=‖x‖,
则称T是X到Y中的保距算子,如果T又是映射到Y上的,则称T是同构映射,此时称X与Y同构.
第二篇:泛函分析总结
泛函分析知识点小结及应用
第七章 度量空间
§1 度量空间的进一步例子
一 度量空间的定义
设 是任一非空集合,若对于
是任一非空集合,若对于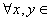
 ,都有唯一确定的实数
,都有唯一确定的实数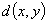 与之对应,且满足
与之对应,且满足
1.非负性: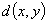
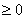 ,
,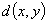 =0
=0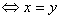 ;
;
2. 对称性:d(x,y)=d(y,x);
3.三角不等式:对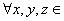
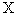 ,都有
,都有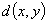
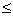
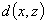 +
+ , 则称(
, 则称(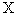 ,
,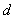 )为度量空间,
)为度量空间,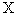 中的元素称为点。
中的元素称为点。
欧氏空间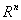 对
对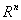 中任意两点
中任意两点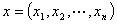 和
和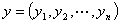 ,规定距离为
,规定距离为 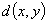 =
=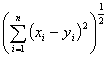 .
.
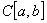 空间
空间 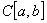 表示闭区间
表示闭区间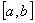 上实值(或复值)连续函数的全体.对
上实值(或复值)连续函数的全体.对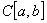 中任意两点
中任意两点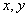 ,定义
,定义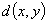 =
=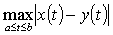 .
.
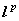 (
(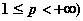 空间 记
空间 记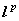 =
=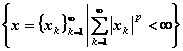 .
.
设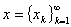 ,
,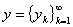
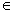
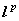 ,定义
,定义 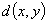 =
=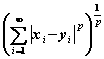 .
.
二 度量空间的进一步例子
例1 序列空间
令 表示实数列(或复数列)的全体,对
表示实数列(或复数列)的全体,对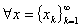 ,
,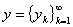 ,令
,令 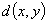 =
=
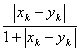 .
.
例2 有界函数空间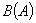
设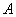 是一个给定的集合,令
是一个给定的集合,令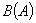 表示
表示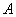 上有界实值(或复值)函数的全体.
上有界实值(或复值)函数的全体. 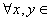
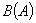 ,定义
,定义 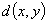 =
=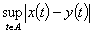 .
.
例3 可测函数空间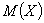
设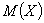 为
为 上实值(或复值)的可测函数的全体,
上实值(或复值)的可测函数的全体,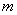 为Lebesgue测度,若
为Lebesgue测度,若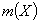
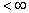 ,对任意两个可测函数
,对任意两个可测函数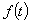 及
及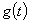 ,由于
,由于 ,故不等式左边为
,故不等式左边为 上可积函数. 令
上可积函数. 令
 =
=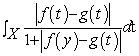 .
.
§2 度量空间中的极限
设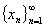 是
是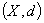 中点列,若
中点列,若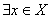 ,s.t.
,s.t.
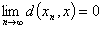 (
(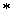 )
)
则称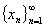 是收敛点列,
是收敛点列, 是点列
是点列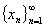 的极限.
的极限.
收敛点列的极限是唯一的. 若设 既牧敛于
既牧敛于 又收敛
又收敛 ,则因为
,则因为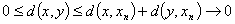
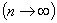 ,而有
,而有 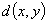 =0. 所以
=0. 所以 =
= .
.
注 (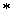 )式换一个表达方式:
)式换一个表达方式: =
=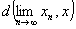 . 即当点列极限存在时,距离运算与极限运算可以换序. 更一般地有
. 即当点列极限存在时,距离运算与极限运算可以换序. 更一般地有
距离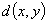 是
是 和
和 的连续函数.
的连续函数.
证明 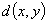
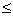
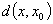 +
+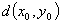 +
+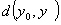
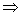
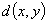 -
-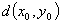
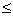
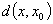 +
+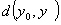 ;
;
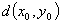
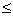
 +
+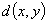 +
+
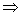
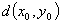 -
-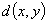
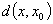 +
+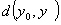 . 所以|
. 所以|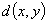 -
-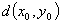 |
|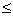
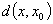 +
+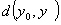
具体空间中点列收敛的具体意义:
1. 欧氏空间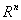
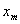 =
=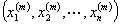 ,
,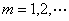 ,为
,为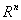 中的点列,
中的点列, =
=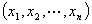
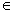
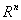 ,
, 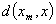 =
=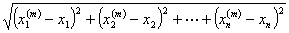 .
. 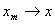
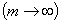
 对每个
对每个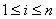 ,有
,有 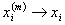
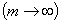 .
.
2. 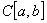 设
设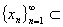
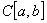 ,
,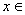
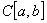 ,则
,则 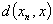 =
=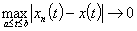
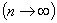

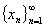 在
在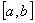 一致收敛于
一致收敛于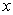 .
.
3. 序列空间 设
设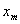 =
=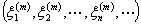 ,
,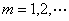 ,及
,及 =
=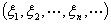 分别是
分别是 中的点列及点,则
中的点列及点,则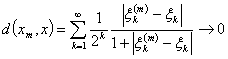
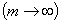

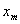 依坐标收敛于
依坐标收敛于 .
.
4. 可测函数空间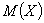 设
设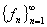
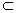
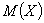 ,
,
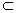
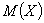 ,则因
,则因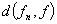 =
=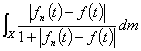 ,有
,有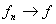

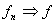 .
.
§3 度量空间中的稠密集 可分空间
定义 设 是度量空间,
是度量空间, 和
和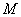 是
是 的两个子集,令
的两个子集,令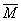 表示
表示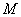 的闭包,若
的闭包,若
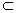
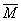 ,则称集
,则称集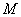 在集
在集 中稠密,当
中稠密,当 =
= 时,称
时,称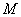 为
为 的一个稠密子集. 若
的一个稠密子集. 若 有一个可数的稠密子集,则称
有一个可数的稠密子集,则称 是可分空间.
是可分空间.
例1 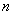 维欧氏空间
维欧氏空间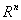 是可分空间. 事实上,坐标为有理数的点的全体是
是可分空间. 事实上,坐标为有理数的点的全体是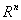 的可数稠密子集.
的可数稠密子集.
例2 离散距离空间 可分
可分 
 是可数集.
是可数集.
例3 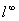 是不可分空间.
是不可分空间.
§4 连续映照
定义 设 =
=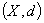 ,
,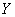 =
=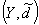 是两个度量空间,
是两个度量空间,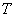 是
是 到
到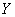 中的映射:
中的映射: =
=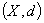
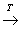
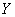 =
=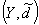 .
. 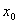
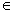
 ,若
,若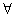
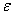
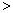 0,
0,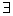
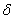
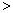 0,s.t.
0,s.t. 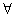

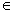
 且
且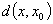

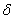 ,都有
,都有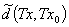

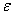 ,则称
,则称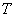 在
在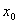 连续:
连续:
定理 1 设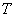 是度量空间
是度量空间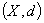 到度量空间
到度量空间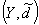 中的映射:
中的映射: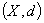
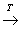
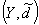 , 则
, 则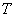 在
在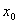 连续
连续  当
当
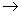
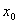 时,必有
时,必有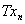
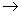
 .
.
定理2 度量空间 到
到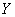 中的映照
中的映照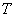 是
是 上的连续映射
上的连续映射  任意开集
任意开集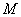
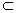
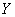 ,
,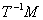 是
是 中的开集.
中的开集.
定理 度量空间
度量空间 到
到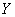 中的映照
中的映照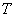 是
是 上的连续映照
上的连续映照  任意闭集
任意闭集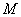
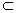
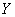 ,
,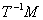 是
是 中的闭集.
中的闭集.
§5 柯西点列和完备度量空间
定义 1 设 =(
=( ,
,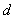 )是度量空间,
)是度量空间,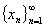 是
是 中的点列. 若
中的点列. 若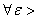 0,
0,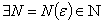 ,s.t.当
,s.t.当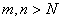 时,有
时,有

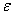 ,则称
,则称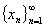 是
是 中的柯西点列或基本点列. 若度量空间(
中的柯西点列或基本点列. 若度量空间( ,
,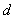 )中每个柯西点列都收敛,则称(
)中每个柯西点列都收敛,则称( ,
,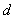 )是完备的度量空间.
)是完备的度量空间.
在一般空间中,柯西点列不一定收敛,如点列1, 1.4, 1,41, 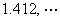 在
在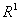 中收敛于
中收敛于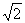 ,在有理数集中不收敛.
,在有理数集中不收敛.
但度量空间中每一个收敛点列都是柯西点列.
定理1 完备度量空间 的子空间
的子空间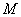 是完备度量空间
是完备度量空间 
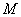 是
是 中的闭子空间.
中的闭子空间.
常见例子:(1)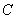 (收敛的实或复数列的全体)是完备度量空间
(收敛的实或复数列的全体)是完备度量空间
(2) 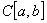 是完备的度量空间
是完备的度量空间
(3) 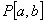 (实系数多项式全体)是不完备的度量空间
(实系数多项式全体)是不完备的度量空间
§6 度量空间的完备化
定义 1 设( ,
,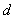 ),(
),(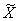 ,
,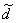 )是两个度量空间,若存在
)是两个度量空间,若存在 到
到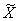 上的保距映射
上的保距映射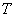 (
(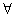
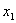 ,
,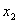
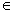
 ,有
,有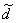 (
(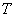
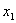 ,
,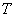
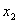 )=
)=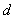 (
(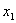 ,
,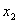 )),则称(
)),则称( ,
,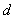 )和(
)和(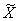 ,
,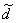 )等距同构,此时称
)等距同构,此时称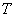 为
为 到
到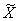 上的等距同构映照。
上的等距同构映照。
等距同构映照是1-1映射. 因设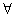
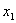 ,
,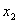
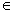
 ,且
,且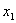
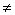
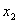 ,则因
,则因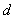 (
(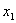 ,
,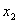 )
) 0及
0及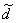 (
(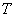
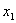 ,
,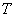
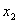 )=
)=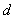 (
(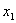 ,
,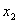 )
)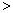 0,知
0,知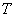
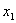
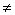
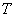
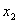 .
.
定理1 (度量空间的完备化定理) 设 =(
=( ,
,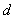 )是度量空间,那么一定存在一完备度量空间
)是度量空间,那么一定存在一完备度量空间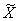 =(
=(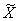 ,
,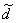 ),使
),使 与
与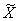 的其个稠密子空间
的其个稠密子空间 等距同构,并且
等距同构,并且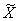 在等距同构意义下是唯一的,即若(
在等距同构意义下是唯一的,即若( ,
,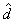 )也是一完备度量空间,且
)也是一完备度量空间,且 与
与 的其个稠密子空间
的其个稠密子空间 等距同构,则(
等距同构,则(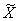 ,
,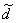 )与(
)与( ,
,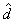 )等距同构.
)等距同构.
§7压缩映照原理及其应用
定义 设 是度量空间,
是度量空间,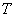 是
是 到
到 中的压映照,若存在一个数
中的压映照,若存在一个数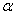 :0
:0
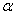
 1,s.t.
1,s.t. 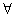
 、
、
 ,成立
,成立
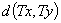
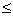
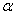
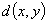
则称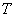 是
是 到
到 中的压缩映照(简称压缩映照).
中的压缩映照(简称压缩映照).
定理1.(压缩映射定理) 设 是完备度量空间,
是完备度量空间,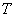 是
是 上的压缩映照,则
上的压缩映照,则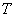 有且只有一个不动点(即方程
有且只有一个不动点(即方程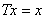 有且只有一个解).
有且只有一个解).
补充定义:若TX=X,则称X是T的不动点,即X是T的不动点 X是方程TX=X的解。
X是方程TX=X的解。
定理2. 设函数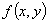 在带状域
在带状域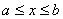 ,
,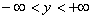 中处处连续,且处处有关于
中处处连续,且处处有关于 的偏导数
的偏导数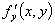 ,若存在常数
,若存在常数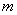 和
和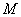 , 满足
, 满足 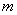

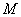 ,0
,0
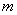
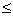
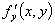
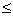
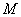 , 则方程
, 则方程 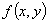 =0 在区间
=0 在区间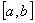 上必有唯一的连续函数
上必有唯一的连续函数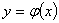 作为解:
作为解: 0,
0,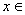
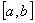 .
.
§8赋范线性空间和Banach空间
线性空间+范数Þ线性赋范空间线性赋范空间+完备性Þ巴拿赫空间
定义1 设X是任一非空集合,若K是一个数域(R或C),如果X对某种规定的加法和数乘两种运算封闭,且"x,y,zÎX, l,ÎmK, 满足:
1) x+y=y+x (加法交换律)
2) (x+y)+z+x+(x+y) (加法结合律)
3) Îq$X, 使x+q=x (零元素存在性)
4) $x’ÎX,使x+x’=q (逆元存在性)
5) l(mx)=mlx=m(lx) (数乘结合律)
6) 1x=x, 0x=q
7) (l+m)x=lx+mx (元素对数的加法分配律)
8) l(x+y)=lx+ly (数对元素的加法分配律)
则称x+y为x与y的和,lx为数l与x的数乘 , 称X为线性空间或向量空间 (实或复),X中的元素称为向量。
定义(范数,赋范线性空间) 设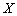 为是实(或复)数域
为是实(或复)数域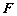 的线性空间,若对
的线性空间,若对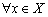 ,存在一个实数
,存在一个实数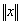 于之对应,且满足下列条件:
于之对应,且满足下列条件:
(1)  ; 且
; 且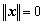

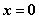 ; (非负性)
; (非负性)
(2) 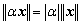 ,
,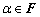 ; (正齐(次)性)
; (正齐(次)性)
(3)  ,
,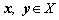 ; (三角不等式)
; (三角不等式)
则称 为
为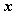 的范数(norm),称
的范数(norm),称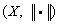 (或:
(或: )为赋范线性空间
)为赋范线性空间
定义 完备的赋范线性空间称为巴拿赫(Banach)空间。
例子: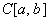 ,空间
,空间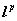 ,
,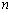 维Euclidean空间
维Euclidean空间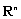 ,
,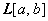 ,
,
都是Banach空间。
度量空间与赋范线性空间 区别:度量空间是定义了度量的线性空间,也就是两个元素之间的“长度”,满足非负性、对称性、三角不等式。赋范线性空间就是定义了范数的线性空间,其满足范数公理(非负性,齐次性,三角不等式)
联系:都是在线性空间的前提下讨论的。赋范线性空间是一种特殊的度量空间
