线性代数公式汇总
1、行列式
1.  行列式共有
行列式共有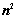 个元素,展开后有
个元素,展开后有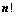 项,可分解为
项,可分解为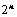 行列式;
行列式;
2. 代数余子式的性质:
①、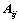 和
和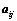 的大小无关;
的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0;
③、某行(列)的元素乘以该行(列)元素的代数余子式为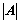 ;
;
3. 代数余子式和余子式的关系:
4. 设 行列式
行列式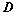 :
:
将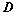 上、下翻转或左右翻转,所得行列式为
上、下翻转或左右翻转,所得行列式为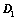 ,则
,则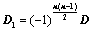 ;
;
将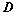 顺时针或逆时针旋转
顺时针或逆时针旋转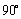 ,所得行列式为
,所得行列式为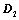 ,则
,则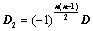 ;
;
将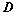 主对角线翻转后(转置),所得行列式为
主对角线翻转后(转置),所得行列式为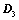 ,则
,则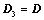 ;
;
将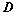 主副角线翻转后,所得行列式为
主副角线翻转后,所得行列式为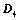 ,则
,则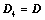 ;
;
5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
②、副对角行列式:副对角元素的乘积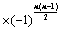 ;
;
③、上、下三角行列式(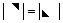 ):主对角元素的乘积;
):主对角元素的乘积;
④、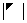 和
和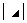 :副对角元素的乘积
:副对角元素的乘积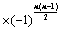 ;
;
⑤、拉普拉斯展开式: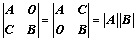 、
、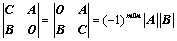
⑥、范德蒙行列式:大指标减小指标的连乘积;
⑦、特征值;
6. 对于 阶行列式
阶行列式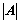 ,恒有:
,恒有: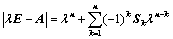 ,其中
,其中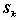 为
为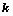 阶主子式;
阶主子式;
7. 证明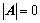 的方法:
的方法:
①、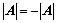 ;
;
②、反证法;
③、构造齐次方程组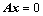 ,证明其有非零解;
,证明其有非零解;
④、利用秩,证明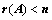 ;
;
⑤、证明0是其特征值;
2、矩阵
1.  是
是 阶可逆矩阵:
阶可逆矩阵:
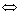
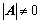 (是非奇异矩阵);
(是非奇异矩阵);
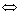
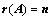 (是满秩矩阵)
(是满秩矩阵)
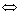
 的行(列)向量组线性无关;
的行(列)向量组线性无关;
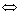 齐次方程组
齐次方程组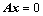 有非零解;
有非零解;
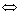
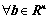 ,
,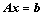 总有唯一解;
总有唯一解;
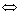
 与
与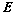 等价;
等价;
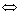
 可表示成若干个初等矩阵的乘积;
可表示成若干个初等矩阵的乘积;
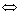
 的特征值全不为0;
的特征值全不为0;
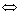
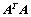 是正定矩阵;
是正定矩阵;
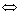
 的行(列)向量组是
的行(列)向量组是 的一组基;
的一组基;
 是
是 中某两组基的过渡矩阵;
中某两组基的过渡矩阵;
2. 对于 阶矩阵
阶矩阵 :
: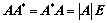 无条件恒成立;
无条件恒成立;
3. 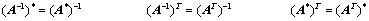
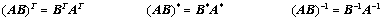
4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;
5. 关于分块矩阵的重要结论,其中均 、
、 可逆:
可逆:
若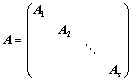 ,则:
,则:
Ⅰ、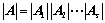 ;
;
Ⅱ、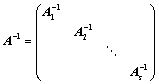 ;
;
②、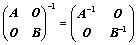 ;(主对角分块)
;(主对角分块)
③、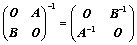 ;(副对角分块)
;(副对角分块)
④、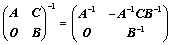 ;(拉普拉斯)
;(拉普拉斯)
⑤、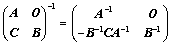 ;(拉普拉斯)
;(拉普拉斯)
3、矩阵的初等变换与线性方程组
1. 一个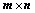 矩阵
矩阵 ,总可经过初等变换化为标准形,其标准形是唯一确定的:
,总可经过初等变换化为标准形,其标准形是唯一确定的: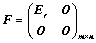 ;
;
等价类:所有与 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
对于同型矩阵 、
、 ,若
,若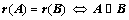 ;
;
2. 行最简形矩阵:
①、只能通过初等行变换获得;
②、每行首个非0元素必须为1;
③、每行首个非0元素所在列的其他元素必须为0;
3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)
①、若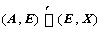 ,则
,则 可逆,且
可逆,且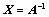 ;
;
②、对矩阵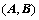 做初等行变化,当
做初等行变化,当 变为
变为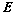 时,
时, 就变成
就变成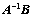 ,即:
,即: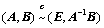 ;
;
③、求解线形方程组:对于 个未知数
个未知数 个方程
个方程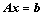 ,如果
,如果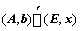 ,则
,则 可逆,且
可逆,且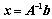 ;
;
4. 初等矩阵和对角矩阵的概念:
①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;
②、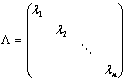 ,左乘矩阵
,左乘矩阵 ,
,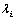 乘
乘 的各行元素;右乘,
的各行元素;右乘,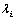 乘
乘 的各列元素;
的各列元素;
③、对调两行或两列,符号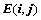 ,且
,且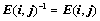 ,例如:
,例如: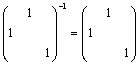 ;
;
④、倍乘某行或某列,符号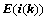 ,且
,且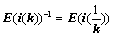 ,例如:
,例如: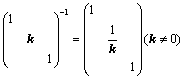 ;
;
⑤、倍加某行或某列,符号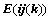 ,且
,且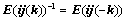 ,如:
,如: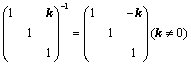 ;
;
5. 矩阵秩的基本性质:
①、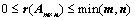 ;
;
②、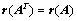 ;
;
③、若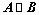 ,则
,则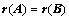 ;
;
④、若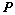 、
、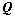 可逆,则
可逆,则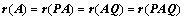 ;(可逆矩阵不影响矩阵的秩)
;(可逆矩阵不影响矩阵的秩)
⑤、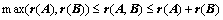 ;(※)
;(※)
⑥、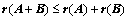 ;(※)
;(※)
⑦、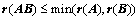 ;(※)
;(※)
⑧、如果 是
是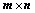 矩阵,
矩阵, 是
是 矩阵,且
矩阵,且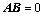 ,则:(※)
,则:(※)
Ⅰ、 的列向量全部是齐次方程组
的列向量全部是齐次方程组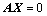 解(转置运算后的结论);
解(转置运算后的结论);
Ⅱ、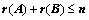
⑨、若 、
、 均为
均为 阶方阵,则
阶方阵,则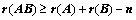 ;
;
6. 三种特殊矩阵的方幂:
①、秩为1的矩阵:一定可以分解为列矩阵(向量)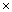 行矩阵(向量)的形式,再采用结合律;
行矩阵(向量)的形式,再采用结合律;
②、型如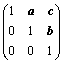 的矩阵:利用二项展开式;
的矩阵:利用二项展开式;
二项展开式: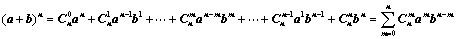 ;
;
注:Ⅰ、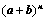 展开后有
展开后有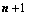 项;
项;
Ⅱ、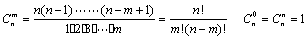
Ⅲ、组合的性质: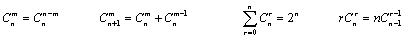 ;
;
③、利用特征值和相似对角化:
7. 伴随矩阵:
①、伴随矩阵的秩: ;
;
②、伴随矩阵的特征值: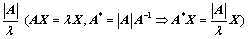 ;
;
③、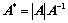 、
、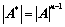
8. 关于 矩阵秩的描述:
矩阵秩的描述:
①、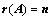 ,
, 中有
中有 阶子式不为0,
阶子式不为0,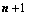 阶子式全部为0;(两句话)
阶子式全部为0;(两句话)
②、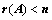 ,
, 中有
中有 阶子式全部为0;
阶子式全部为0;
③、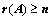 ,
, 中有
中有 阶子式不为0;
阶子式不为0;
9. 线性方程组: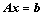 ,其中
,其中 为
为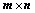 矩阵,则:
矩阵,则:
①、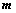 与方程的个数相同,即方程组
与方程的个数相同,即方程组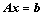 有
有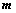 个方程;
个方程;
②、 与方程组得未知数个数相同,方程组
与方程组得未知数个数相同,方程组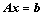 为
为 元方程;
元方程;
10. 线性方程组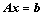 的求解:
的求解:
①、对增广矩阵 进行初等行变换(只能使用初等行变换);
进行初等行变换(只能使用初等行变换);
②、齐次解为对应齐次方程组的解;
③、特解:自由变量赋初值后求得;
11. 由 个未知数
个未知数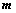 个方程的方程组构成
个方程的方程组构成 元线性方程:
元线性方程:
①、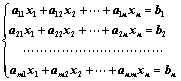 ;
;
②、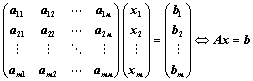 (向量方程,
(向量方程, 为
为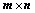 矩阵,
矩阵,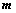 个方程,
个方程, 个未知数)
个未知数)
③、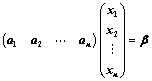 (全部按列分块,其中
(全部按列分块,其中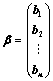 );
);
④、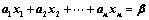 (线性表出)
(线性表出)
⑤、有解的充要条件: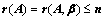 (
( 为未知数的个数或维数)
为未知数的个数或维数)
4、向量组的线性相关性
1. 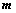 个
个 维列向量所组成的向量组
维列向量所组成的向量组 :
: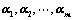 构成
构成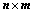 矩阵
矩阵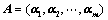 ;
;
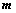 个
个 维行向量所组成的向量组
维行向量所组成的向量组 :
: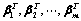 构成
构成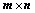 矩阵
矩阵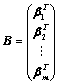 ;
;
含有有限个向量的有序向量组与矩阵一一对应;
2. ①、向量组的线性相关、无关 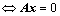 有、无非零解;(齐次线性方程组)
有、无非零解;(齐次线性方程组)
②、向量的线性表出 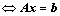 是否有解;(线性方程组)
是否有解;(线性方程组)
③、向量组的相互线性表示 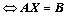 是否有解;(矩阵方程)
是否有解;(矩阵方程)
3. 矩阵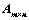 与
与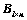 行向量组等价的充分必要条件是:齐次方程组
行向量组等价的充分必要条件是:齐次方程组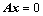 和
和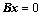 同解;(
同解;( 例14)
例14)
4. 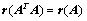 ;(
;( 例15)
例15)
5.  维向量线性相关的几何意义:
维向量线性相关的几何意义:
①、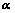 线性相关
线性相关 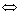
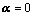 ;
;
②、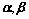 线性相关
线性相关 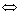
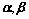 坐标成比例或共线(平行);
坐标成比例或共线(平行);
③、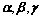 线性相关
线性相关 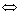
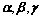 共面;
共面;
6. 线性相关与无关的两套定理:
若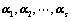 线性相关,则
线性相关,则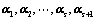 必线性相关;
必线性相关;
若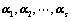 线性无关,则
线性无关,则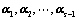 必线性无关;(向量的个数加加减减,二者为对偶)
必线性无关;(向量的个数加加减减,二者为对偶)
若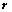 维向量组
维向量组 的每个向量上添上
的每个向量上添上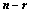 个分量,构成
个分量,构成 维向量组
维向量组 :
:
若 线性无关,则
线性无关,则 也线性无关;反之若
也线性无关;反之若 线性相关,则
线性相关,则 也线性相关;(向量组的维数加加减减)
也线性相关;(向量组的维数加加减减)
简言之:无关组延长后仍无关,反之,不确定;
7. 向量组 (个数为
(个数为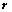 )能由向量组
)能由向量组 (个数为
(个数为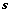 )线性表示,且
)线性表示,且 线性无关,则
线性无关,则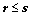 (二版
(二版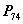 定理7);
定理7);
向量组 能由向量组
能由向量组 线性表示,则
线性表示,则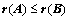 ;(
;(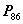 定理3)
定理3)
向量组 能由向量组
能由向量组 线性表示
线性表示
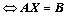 有解;
有解;
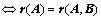 (
(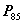 定理2)
定理2)
向量组 能由向量组
能由向量组 等价
等价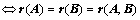 (
( 定理2推论)
定理2推论)
8. 方阵 可逆
可逆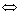 存在有限个初等矩阵
存在有限个初等矩阵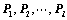 ,使
,使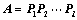 ;
;
①、矩阵行等价: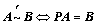 (左乘,
(左乘,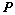 可逆)
可逆)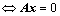 与
与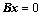 同解
同解
②、矩阵列等价: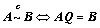 (右乘,
(右乘,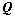 可逆);
可逆);
③、矩阵等价: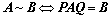 (
(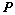 、
、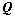 可逆);
可逆);
9. 对于矩阵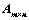 与
与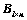 :
:
①、若 与
与 行等价,则
行等价,则 与
与 的行秩相等;
的行秩相等;
②、若 与
与 行等价,则
行等价,则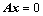 与
与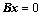 同解,且
同解,且 与
与 的任何对应的列向量组具有相同的线性相关性;
的任何对应的列向量组具有相同的线性相关性;
③、矩阵的初等变换不改变矩阵的秩;
④、矩阵 的行秩等于列秩;
的行秩等于列秩;
10. 若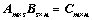 ,则:
,则:
①、 的列向量组能由
的列向量组能由 的列向量组线性表示,
的列向量组线性表示, 为系数矩阵;
为系数矩阵;
②、 的行向量组能由
的行向量组能由 的行向量组线性表示,
的行向量组线性表示,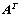 为系数矩阵;(转置)
为系数矩阵;(转置)
11. 齐次方程组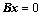 的解一定是
的解一定是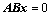 的解,考试中可以直接作为定理使用,而无需证明;
的解,考试中可以直接作为定理使用,而无需证明;
①、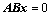 只有零解
只有零解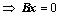 只有零解;
只有零解;
②、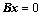 有非零解
有非零解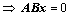 一定存在非零解;
一定存在非零解;
12. 设向量组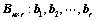 可由向量组
可由向量组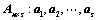 线性表示为:(
线性表示为:(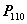 题19结论)
题19结论)
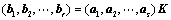 (
(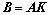 )
)
其中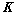 为
为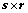 ,且
,且 线性无关,则
线性无关,则 组线性无关
组线性无关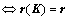 ;(
;( 与
与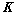 的列向量组具有相同线性相关性)
的列向量组具有相同线性相关性)
(必要性: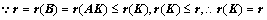 ;充分性:反证法)
;充分性:反证法)
注:当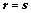 时,
时,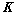 为方阵,可当作定理使用;
为方阵,可当作定理使用;
13. ①、对矩阵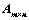 ,存在
,存在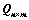 ,
,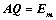
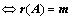 、
、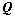 的列向量线性无关;(
的列向量线性无关;(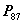 )
)
②、对矩阵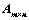 ,存在
,存在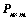 ,
,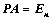
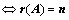 、
、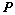 的行向量线性无关;
的行向量线性无关;
14. 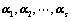 线性相关
线性相关
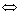 存在一组不全为0的数
存在一组不全为0的数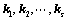 ,使得
,使得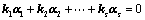 成立;(定义)
成立;(定义)
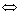
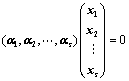 有非零解,即
有非零解,即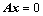 有非零解;
有非零解;
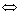
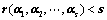 ,系数矩阵的秩小于未知数的个数;
,系数矩阵的秩小于未知数的个数;
15. 设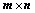 的矩阵
的矩阵 的秩为
的秩为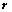 ,则
,则 元齐次线性方程组
元齐次线性方程组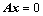 的解集
的解集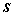 的秩为:
的秩为: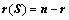 ;
;
16. 若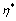 为
为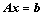 的一个解,
的一个解,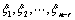 为
为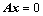 的一个基础解系,则
的一个基础解系,则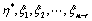 线性无关;(
线性无关;(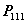 题33结论)
题33结论)
5、相似矩阵和二次型
1. 正交矩阵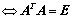 或
或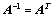 (定义),性质:
(定义),性质:
①、 的列向量都是单位向量,且两两正交,即
的列向量都是单位向量,且两两正交,即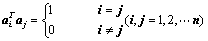 ;
;
②、若 为正交矩阵,则
为正交矩阵,则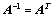 也为正交阵,且
也为正交阵,且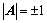 ;
;
③、若 、
、 正交阵,则
正交阵,则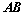 也是正交阵;
也是正交阵;
注意:求解正交阵,千万不要忘记施密特正交化和单位化;
2. 施密特正交化: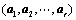
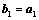 ;
;
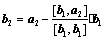

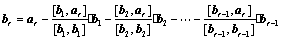 ;
;
3. 对于普通方阵,不同特征值对应的特征向量线性无关;
对于实对称阵,不同特征值对应的特征向量正交;
4. ①、 与
与 等价
等价 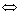
 经过初等变换得到
经过初等变换得到 ;
;
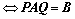 ,
,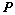 、
、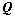 可逆;
可逆;
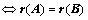 ,
, 、
、 同型;
同型;
②、 与
与 合同
合同 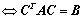 ,其中可逆;
,其中可逆;
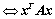 与
与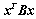 有相同的正、负惯性指数;
有相同的正、负惯性指数;
③、 与
与 相似
相似 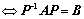 ;
;
5. 相似一定合同、合同未必相似;
若 为正交矩阵,则
为正交矩阵,则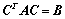
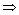
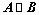 ,(合同、相似的约束条件不同,相似的更严格);
,(合同、相似的约束条件不同,相似的更严格);
6.  为对称阵,则
为对称阵,则 为二次型矩阵;
为二次型矩阵;
7.  元二次型
元二次型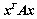 为正定:
为正定:
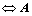 的正惯性指数为
的正惯性指数为 ;
;
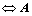 与
与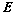 合同,即存在可逆矩阵
合同,即存在可逆矩阵 ,使
,使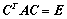 ;
;
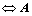 的所有特征值均为正数;
的所有特征值均为正数;
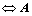 的各阶顺序主子式均大于0;
的各阶顺序主子式均大于0;
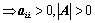 ;(必要条件)
;(必要条件)
加油~~~~~~~~~~~~~~
~~~~~~~
·
~
~
~
~
~
~
~
第二篇:线性代数部分公式合集
线性代数部分
梳理:条理化,给出一个系统的,有内在有机结构的理论体系。
沟通:突出各部分内容间的联系。
充实提高:围绕考试要求,介绍一些一般教材上没有的结果,教给大家常见问题的实用而简捷的方法。 大家要有这样的思想准备:发现我的讲解在体系上和你以前学习的有所不同,有的方法是你不知道的。但是我相信,只要你对它们了解了,掌握了,会提高你的解题能力的。
基本运算
①A?B?B?A
②?A?B??C?A??B?C?
③c?A?B??cA?cB ?c?d?A?cA?dA
④c?dA???cd?A
⑤cA?0?c?0或A?0。
?AT?T?A
?A?B?T?AT?BT
?cA?T?c?AT?。
?AB?T?BTAT
??n?n?1??21??C21?
n?n?n?
2
D?a21A21?a22A22???a2nA2n 转置值不变AT?A 逆值变A?1?1
A
cA?cnA
,?1??2,??,?1,??,?2,?
A???1,?2,?3?,3阶矩阵
B???1,?2,?3?
A?B?A?B
A?B???1??1,?2??2,?3??3?
- 1 -
A?B?1??1,?2??2,?3??3
A?
0B?A0
?B?AB
E?i,j?c???1
有关乘法的基本运算
Cij?ai1b1j?ai2b2j???ainbnj
线性性质 ?A1?A2?B?A1B?A2B,
A?B1?B2??AB1?AB2
?cA?B?c?AB??A?cB?
结合律 ?AB?C?A?BC?
?AB?T?BTAT
AB?AB
AkAl?Ak?l
?Ak?l?Akl
?AB?k?AkBk不一定成立!
AE?A,EA?A
A?kE??kA,?kE?A?kA
AB?E?BA?E
与数的乘法的不同之处
?AB?k?AkBk不一定成立!
无交换律 因式分解障碍是交换性
一个矩阵A的每个多项式可以因式分解,例如 A2?2A?3E??A?3E??A?E? 无消去律(矩阵和矩阵相乘)
当AB?0时??A?0或B?0
由A?0和AB?0??B?0
由A?0时AB?AC??B?C(无左消去律)
特别的 设A可逆,则A有消去律。
左消去律:AB?AC?B?C。 右消去律:BA?CA?B?C。
如果A列满秩,则A有左消去律,即
- 2 -
①AB?0?B?0 ②AB?AC?B?C
可逆矩阵的性质 i)当A可逆时,
A也可逆,且A
T
??
T?1
?A?1。 ?A?1。
?1
??
T
A也可逆,且A
k
??
k?1
??
k
数c?0,cA也可逆,?cA?
?
1?1
A。 c
?1
ii)A,B是两个n阶可逆矩阵?AB也可逆,且?AB?
?B?1A?1。
推论:设A,B是两个n阶矩阵,则AB?E?BA?E 命题:初等矩阵都可逆,且 ?E?i,j??
?1
?E?i,j? ??1???E??i?c???
????
?1
?E?i?c???
?1
?E?i,j?c????E?i,j??c??
命题:准对角矩阵
A11
A?
000
0A2200
00
00
可逆?每个Aii都可逆,记A
?1
?1A11
?1A22
00?0
000
?1Akk
?00Akk
?
000
00
伴随矩阵的基本性质: AA*?A*A?AE 当A可逆时, A
A* (求逆矩阵的伴随矩阵法) ?E A- 3 -
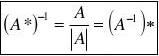
伴随矩阵的其他性质
??1?A*?A?1A?1???????1A??? A?? A*?AA
T?1 ②A*??A*?, T??
③cA*?cn?1A* ④?AB?*?B*A*,
⑤A*??A*?, kk??
?a?b? n?2时, ?A*?*?A A*????cd?? ?? 关于矩阵右上肩记号:T,k,?1,*
i) 任何两个的次序可交换,
如A*??A*?, TT??
?1 ?A*??A?1*等
TT?1?? ii) ?AB??BA, ?AB?T?B?1A?1,
?AB?*?B*A*
但AB?BA不一定成立! kkk
线性表示
0??1,?2,?,?s
?i??1,?2,?,?s
???1,?2,?,?s?x1?1?x2?2???xs?s??有解 ?
Ax???1,?2,?,?s?x??有解?x??x1,?,xs?T? ?有解,即?可用A的列向量组表示 AB?C??r1,r2,?,rs?,A???1,?2,?,?n?, 则r1,r2,?,rs??1,?2,?,?n。
- 4 -
?1,?2,?,?t??1,?2,?,?s,
则存在矩阵C,使得??1,?2,?,?t????1,?2,?,?s?C
线性表示关系有传递性 当?1,?2,?,?t??1,?2,?,?s?r1,r2,?,rp, 则?1,?2,?,?t?r1,r2,?,rp。 等价关系:如果?1,?2,?,?s与?1,?2,?,?t互相可表示 记作?1,?2,?,?s?
线性相关
s?1,单个向量?,x??0 ?1,?2,?,?s???1,?2,?,?t ?1,?2,?,?t。 ?相关???0
?1,?2相关?a1:b1?a2:b2???an:bn
s?2,?1,?2相关?对应分量成比例

A???1,?2,?,?n?,Ax?0有非零解?A?0 如果s?n,则?1,?2,?,?s一定相关
Ax?0的方程个数n?未知数个数s ②如果?1,?2,?,?s无关,则它的每一个部分组都无关 ③如果?1,?2,?,?s无关,而?1,?2,?,?s,?相关,则???1,?2,?,?s 证明:设c1,?,cs,c不全为0,使得c1?1???cs?s?c??0 则其中c?0,否则c1,?,cs不全为0,c1?1???cs?s?0,与条件?1,?,?s无关矛盾。
于是???cc1?1???s?s。 cc ④当???1,?,?s时,表示方式唯一??1??s无关
- 5 -
(表示方式不唯一??1??s相关)
⑤若?1,?,?t??1,?,?s,并且t?s,则?1,?,?t一定线性相关。 证明:记A???1,?,?s?,B???1,?,?t?,
则存在s?t矩阵C,使得 B?AC。
Cx?0有s个方程,t个未知数,s?t,有非零解?,C??0。 则B??AC??0,即?也是Bx?0的非零解,从而?1,?,?t线性相关。
各性质的逆否形式
①如果?1,?2,?,?s无关,则s?n。
②如果?1,?2,?,?s有相关的部分组,则它自己一定也相关。
③如果?1??s无关,而????1,?,?s,则?1,?,?s?无关。
⑤如果?1??t??1??s,?1??t无关,则t?s。
推论:若两个无关向量组?1??s与?1??t等价,则s?t。
极大无关组
一个线性无关部分组?I?,若#?I?等于秩?1,?2,?4,?6??I?,?I?就一定是极大无关组 ①?1,?2,?,?s无关?? ??1,?2,?,?s??s
②???1,?2,?,?s? ? ??1,?2,?,?s,???? ??1,?,?s?
另一种说法: 取?1,?2,?,?s的一个极大无关组?I?
?I?也是?1,?2,?,?s,?的极大无关组??I?,?相关。 证明:???1,?,?s????I???I?,?相关。
- 6 -
?? ?1,?,?s,???1??s ? ??1,?,?s,??????? ?,?,?1,?/?,?,???1s1s?
③?可用?1,?,?s唯一表示?? ??1,?,?s,?? ?? ??1,?,?s??s ④?1,?,?t??1,?,?s?? ??1,?,?s,?1,?,?t??? ??1,?,?s?
?? ??1,?,?t??? ??1,?,?s?
⑤?1,?,?s??1,?,?t?? ??1,?,?s??? ??1??s,?1??t??? ??1,?,?t?
矩阵的秩的简单性质
0?r?A??min?m,n?
r?A??0?A?0
A行满秩:r?A??m
A列满秩:r?A??n
n阶矩阵A满秩:r?A??n
A满秩?A的行(列)向量组线性无关
?A?0
?A可逆
?Ax?0只有零解,Ax?
矩阵在运算中秩的变化
初等变换保持矩阵的秩
①rA?唯一解。 ???r?A? T
②c?0时,r?cA??r?A?
③r?A?B??r?A??r?B?
④r?AB??min?r?A?,r?B??
⑤A可逆时,r?AB??r?B?
弱化条件:如果A列满秩,则??AB????B?
证:下面证ABx?0与Bx?0同解。
- 7 -
?是ABx?0的解?AB??0
?B??0??是Bx?0的解
B可逆时,r?AB??r?A?
⑥若AB?0,则r?A??r?B??n(A的列数,B的行数) ⑦A列满秩时r?AB??r?B?
B行满秩时r?AB??r?A?
⑧r?AB??n?r?A??r?B?
解的性质
1.Ax?0的解的性质。
如果?1,?2,?,?e是一组解,则它们的任意线性组合c1?1 ?i,A?i?0?A?c1?1?c2?2???ce?e??0 2.Ax??c2?2???ce?e一定也是解。 ????0?
①如果?1,?2,?,?e是Ax??的一组解,则
?的解?c1?c2???ce?1 c1?1?c2?2???ce?e也是Ax?
c1?1?c2?2???ce?e是Ax?0的解?c1?c2???ce?0 A?i????i
A?c1?1?c2?2???ce?e??c1A?1?c2A?2???ceA?e ??c1?c2???ce?? 特别的: 当?1,?2是Ax?
②如果?0是Ax?
解的情况判别
方程:Ax?
??的两个解时,?1??2是Ax?0的解 ?的解,则n维向量?也是Ax??的解????0是Ax?0的解。 ?,即x1?1?x2?2???xn?n?? ???1,?2,?,?n
???A|?????A?????1,?2,?,?n,??????1,?2,?,?n?
- 8 -
???A|?????A? ???A|?????A??n ???A|?????A??n
方程个数m:
??A|???m,??A??m
①当??A??m时,??A|???m,有解
②当m?n时,??A??n,不会是唯一解
对于齐次线性方程组Ax?0,
只有零解???A??n(即A列满秩)
(有非零解???A??n

)
特征值特征向量
两种特殊情形:
(1)A是上(下)三角矩阵,对角矩阵时,特征值即对角线上的元素。
?? 1**?
A???0? ??
?2?
?00? 3??
x?? 1?*?*
xE?A?0x?? 2????x?? 1??x?? 2??x?? 3?
00x?? 3
(2)r?A??1时:A的特征值为0,0,?,0,tr?A?
特征值的性质
命题:n阶矩阵A的特征值?的重数?n?r?? E?A? 命题:设A的特征值为? 1,? 2,?,? n,则
②? 1?? 2???? n?trA 命题:设?是A的特征向量,特征值为?,即A????,则
- 9 -
①对于A的每个多项式f?A?,f?A???f?x??
②当A可逆时,A?1??1?,A*??|A|
???
命题:设A的特征值为? 1,? 2,?,? n,则
①f?A?的特征值为f?? 1?,f?? 2?,?,f?? n?
②A可逆时,A?1的特征值为11
? ,?,?,1
1 2? n
A*的特征值为|A||A|
? ,,?,|A|
1? 2? n
③AT的特征值也是? 1,? 2,?,? n
特征值的应用
①求行列式|A|?? 1,? 2,?,? n
②判别可逆性

A?? E可逆??不是A的特征值。
当f?A??0时,如果f?c??0,则A?cE可逆
若?是A的特征值,则f???是f?A?的特征值?f????0。 f?c??0?c不是A的特征值?AcE可逆。
n阶矩阵的相似关系
当AU?UA时,B?A,而AU?UA时,B?A。 相似关系有i)对称性:A~B?B~A
U?1AU?B,则A?UBU?1
ii)有传递性:A~B,B~C,则A~C
U?1AU?B,V?1BV?C,则
?UV??1A?UV??V?1U?1AUV?V?1BV?C 命题 当A~B时,A和B有许多相同的性质
①A?B
②??A????B?
③A,B的特征多项式相同,从而特征值完全一致。
- 10 -
A与B的特征向量的关系:?是A的属于?的特征向量?U?1?是B的属于?的特征向量。
A?????BU?1???U?1?
? ?
正定二次型与正定矩阵性质与判别
可逆线性变换替换保持正定性 ?????? U?1A???U?1??U?1AUU?1???U?1?
f?x1,x2,?,xn?变为g?y1,y2,?,yn?,则它们同时正定或同时不正定
A~?B,则A,B同时正定,同时不正定。
例如B?CTAC。如果A正定,则对每个x?0
xTBx?xTCTACx??Cx?TACx?0
(C可逆,x?0,?Cx?0!)
我们给出关于正定的以下性质
A正定?A~?E
?存在实可逆矩阵C,A?CTC。
?A的正惯性指数?n。
?A的特征值全大于0。
?A的每个顺序主子式全大于0。
判断A正定的三种方法:
①顺序主子式法。
②特征值法。
③定义法。
- 11 -
基本概念
对称矩阵A?A。
反对称矩阵A??A。
简单阶梯形矩阵:台角位置的元素都为1 ,台角正上方的元素都为0。 如果A是一个n阶矩阵,A是阶梯形矩阵?A是上三角矩阵,反之不一定 矩阵消元法:(解的情况)
①写出增广矩阵A?,用初等行变换化A?为阶梯形矩阵B?。 ②用B?判别解的情况。
i)如果B?最下面的非零行为0,?,0d,则无解,否则有解。 ii)如果有解,记?是B?的非零行数,则
? ?n时唯一解。
??n时无穷多解。
iii)唯一解求解的方法(初等变换法)
去掉B的零行,得B0 ?0,它是n??n?c?矩阵,B0是n阶梯形矩阵,从而是上三角矩阵。 则bn n?0?bn?1 n?1?0??bii都不为0。
A????Br???E ?就是解。
TT????????????????????行??行??
a11
一个n阶行列式a12a22?a1n?a2n的值: a21
?
an1???an2?ann
①是n!项的代数和
②每一项是n个元素的乘积,它们共有n!项 a1j1a2j2?anjn其中j1j2?jn是1,2,?,n的一个全排列。 ③a1j1?anjn 前面乘的应为??1???j1j2?jn? ??j1j2?jn?的逆序数 ?
j1j2?jn???1???j1j2?jn?a1j1a2j2?anjn
??n?n?1??21??Cn2?
代数余子式
Mij为aij的余子式。 n?n?1? 2
- 12 -
Aij???1?i?jMij
定理:一个行列式的值D等于它的某一行(列),各元素与各自代数余子式乘积之和。
D?a21A21?a22A22???a2nA2n
一行(列)的元素乘上另一行(列)的相应元素代数余子式之和为0。
范德蒙行列式
1a11?1a1?an2??(aj?ai) Cn个
i?j
乘法相关
AB的?i,j?位元素是A的第i行和B的第j列对应元素乘积之和。
Cij?ai1b1j?ai2b2j???ainbnj
乘积矩阵的列向量与行向量
(1)设m?n矩阵A???1,?2,?,?n?,n维列向量???b1,b2,?,bn?,则 T
A??b1?1?b2?2???bn?n
矩阵乘法应用于方程组
方程组的矩阵形式
Ax??,???b1,b2,?,bm?T
? ?? 方程组的向量形式 x1?1?x2?2???xn?n?
(2)设AB?C,
AB??A?1,A?2,?,A?s?
ri?A?i?b1i?1?b2i?2???bni?n
AB的第i个列向量是A的列向量组的线性组合,组合系数是B的第i个列向量的各分量。 AB的第i个行向量是B的行向量组的线性组合,组合系数是A的第i个行向量的各分量。 矩阵分解
当矩阵C的每个列向量都是A的列向量的线性组合时,可把C分解为A与一个矩阵B的乘积
特别的在有关对角矩阵的乘法中的若干问题
- 13 -
0???200? ???1?1,?2?2,?,?n?n? 0?0??00?n??
对角矩阵从右侧乘一矩阵A,即用对角线上的元素依次乘A的各列向量 对角矩阵从左侧乘一矩阵A,即用对角线上的元素依次乘A的各行向量 于是AE?A,EA?A
A?kE??kA,?kE?A?kA
两个对角矩阵相乘只须把对角线上对应元素相乘
对角矩阵的k次方幂只须把每个对角线上元素作k次方幂
对一个n阶矩阵A,规定tr?A?为A的对角线上元素之和称为A的迹数。 于是 ??1??0 ??1,?2,?,?n??0??0?00?????????TkTk?1??T??tr???T????T ?T??tr???T? k?1
其他形式方阵的高次幂也有规律
?101??? 例如:A??020?
?101???
初等矩阵及其在乘法中的作用
(1)E?i,j?:交换E的第i,j两行或交换E的第i,j两列
(2)E?i(c)?:用数c??0?乘E的第i行或第i列
(3)E?i,j(c)?:把E的第j行的c倍加到第i行上,或把E的第i列的c倍加到第j列上。 初等矩阵从左(右)侧乘一个矩阵A等同于对A作一次相当的初等行(列)变换
乘法的分块法则
一般法则:在计算两个矩阵A和B的乘积时,可以先把A和B用纵横线分割成若干小矩阵来进行,要求
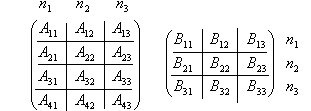
A的纵向分割与B的横向分割一致。
两种常用的情况
(1)A,B都分成4块
A??? ?A11
?A21A12??B11??,B???BA22??21B12?? ?B22?
- 14 -
其中Ai1的列数和B1j的行数相等,Ai2的列数和B2j的行数相关。
AB???AA?AB2221?2111
(2)准对角矩阵 ?A11B11?A12B21A11B12?A12B22?? ?A21B12?A22B22?
?A11??0 ???0?
?A11??0 ????0?0A2200A220???0?? ???Akk???0??B11???0??0????????Akk???0?0B220?00??A11B11???0??0?????????Bkk???0?0A22B22?0???0?? ??AkkBkk??0
矩阵方程与可逆矩阵
两类基本的矩阵方程 (都需求A是方阵,且A?0)
?I?Ax?B ?II?xA?B
(I)的解法:
AB???Ex
(II)的解法,先化为Ax?B。
ABTTT??行???TT???Ex?。 T
通过逆求解:Ax?B,x?AB
可逆矩阵及其逆矩阵
定义:设A是n阶矩阵,如果存在n阶矩阵H,使得AH?E,且HA?E,则称A是可逆矩阵,称H是A的逆矩阵,证作A。
求A的方程(初等变换法) ?1?1?1
??EA AE?
伴随矩阵 ??行??1?
- 15 -
?A11??A12 A*?????A?1n
线性表示
A21?A22?A2nAn1???An2?T?? ?Aij?????Ann?? ?可以用?1,?2,?,?s线性表示,即?可以表示为?1,?2,?,?s的线性组合,
也就是存在c1,c2,?,cs使得 c1?1?c2?2???cs?s?记号:???1,?2,?,?s ?
线性相关性
线性相关:存在向量?i可用其它向量?1,?,?i?1,?i?1,?,?s线性表示。 线性无关:每个向量?i都不能用其它向量线性表示 定义:如果存在不全为0的c1,c2,?,cs,使得c1?1?c2?2???cs?s?0则称?1,?2,?,?s线性相关,否则称?1,?2,?,?s线性无关。
即:?1,?2,?,?s线性相(无)关?x1?1???xs?s?0有(无)非零解
?
极大无关组和秩 ??1,?2,?,?s?x?0有(无)非零解
定义:?1,?2,?,?s的一个部分组?I?称为它的一个极大无关组,如果满足: i)?I?线性无关。
ii)?I?再扩大就相关。
?I????1,?2,?,?s ?II???1??s??I?
定义:规定?1,?2,?,?s的秩? ??1,?2,?,?s??#?I?。
如果?1,?2,?,?s每个元素都是零向量,则规定其秩为0。
0?? ??1,?,?s??min?n,s?
- 16 -
有相同线性关系的向量组
定义:两个向量若有相同个数的向量:?1,?2,?,?s,?1,?2,?,?s,并且向量方程 x1,?1?x2?2???xs?s?0与x1?1?x2?2???xs?s?0同解,则称它们有相同的线性关系。 ①对应的部分组有一致的相关性。
?1,?2,?4的对应部分组?1,?2,?4,
若?1,?2,?4相关,有不全为0的c1,c2,c4使得
c1?1?c2?2?c4?4?0,
即?c1,c2,0,c4,0,?,0?是x1?1?x2?2???xs?s?0的解, 从而也是x1?1?x2?2???xs?s?0的解,则有 c1?1?c2?2?c4?4?0,
?1,?2,?3也相关。
②极大无关组相对应,从而秩相等。
③有一致的内在线表示关系。
设:A???1,?2,?,?s?,B???1,?2,?,?s?,则
x1?1?x2?2???xs?s?0 即 Ax?0,
x1?1?x2?2???xs?s?0 即 Bx?0。
?1,?2,?,?s与?1,?2,?,?s有相同的线性关系即Ax?0与Bx?0同解。 反之,当Ax?0与Bx?0同解时,A和B的列向量组有相同的线性关系。
矩阵的秩
定理:矩阵A的行向量组的秩=列向量组的秩
规定r?A??行(列)向量组的秩。
r?A?的计算:用初等变换化A为阶梯形矩阵B,则B的非零行数即r?A?。 命题:r?A??A的非零子式阶数的最大值。
- 17 -
方程组的表达形式
?a11x1?a12x2???a1nxn?b1?ax?ax???ax?b?2112222nn2 1.?????am1x1?am2x2???amnxn?bm
2.Ax?? ?是解?A???
? 有解????1,?2,?,?n 3.x1?1?x2?2???xn?n?
基础解系和通解
1.Ax?0有非零解时的基础解系
?1,?2,?,?e是Ax?0的基础解系的条件: ①每个?i都是Ax?0的解
②?1,?2,?,?e线性无关
③Ax?0的每个解???1,?2,?,?e
③l?n???A? /
通解
①如果?1,?2,?,?e是Ax?0的一个基础解系,则Ax?0的通解为
c1?1?c2?2???ce?e,ci任意 ②如果?0是Ax?????0?的一个解,?1,?2,?,?e是Ax?0的基础解系,则Ax??的通解为
?0?c1?1?c2?2???ce?e,ci任意
特征向量与特征值
并且A?与?线性相关,则称?是A的一个特征向量。此时,有数?,使得A????, 定义:如果??0,
- 18 -
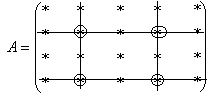
称?为?的特征值。
设A是数量矩阵?E,则对每个n维列向量?,A????,于是,任何非零列向量都是?E的特征向量,特征值都是?。
①特征值有限特征向量无穷多
若A????,A?c???cA??c?????c??
A?1???1? ??A?c1?1?c2?2??c1A?1?c2A?2???c1?1?c2?2? A?2???2?
②每个特征向量有唯一特征值,而有许多特征向量有相同的特征值。
③计算时先求特征值,后求特征向量。
特征向量与特征值计算
A????,??0
???E?A???0,??0
??是??E?A?x?0的非零解
命题:①?是A的特征值?? E?A?0
②?是属于?的特征向量??是?? E?A?x?0的非零解
称多项式xE?A为A的特征多项式。
?是A的特征值??是A的特征多项式xE?A的根。 ?的重数:?作为xE?A的根的重数。
n阶矩阵A的特征值有n个:? 1,? 2,?,? n,可能其中有的不是实数,有的是多重的。
计算步骤:
①求出特征多项式xE?A。
②求xE?A的根,得特征值。
③对每个特征值? i,求?? iE?A?x?0的非零解,得属于? i的特征向量。
n阶矩阵的相似关系
设A,B是两个n阶矩阵。如果存在n阶可逆矩阵U,使得U?1AU?B,则称A与B相似,记作A~B。
- 19 -
n阶矩阵的对角化
基本定理 A可对角化?A有n个线性无关的特征向量。 设可逆矩阵U???1,?2,?,?n?,则
??1??0?1
UAU??
0??0?
?2
00
0??00?
?0?
?0?n??
??1
??0
?A??1,?2,?,?n??U?
0??0?
?2
00
0??00?
???1?1,?2?2,?,?n?n? ??0?0?n??
?A?i??i?i,i?1,2,?,n 判别法则
A可对角化?对于A的每个特征值?,?的重数?n????E?A?。
计算:对每个特征值?i,求出??iE?A?x?0的一个基础解系,把它们合在一起,得到n个线性无关的特征向量,?1,?,?n。令U???1,?2,?,?n?,则
??1
??0?1
UAU??
0??0?
?2
00
0??00?
,其中?i为?i的特征值。 ??0?0?n??
二次型(实二次型) 二次型及其矩阵
一个n元二次型的一般形式为 f?x1,x2,?,xn??
?a
i?1
n
ii
xi2?2?aijxixj
i?j
只有平方项的二次型称为标准二次型。
形如:x1?x2???xp?xp?1???xp?q的n元二次型称为规范二次型。 对每个n阶实矩阵A,记x??x1,x2,?,xn?,则xAx是一个二次型。
T
T
22222
f?x1,x2,?,xn??xAx
T
称A的秩??A?为这个二次型的秩。 标准二次型的矩阵是对角矩阵。
- 20 -
规范二次型的矩阵是规范对角矩阵。
可逆线性变量替换
设有一个n元二次型f?x1,x2,?,xn?,引进新的一组变量y1,y2,?,yn,并把x1,x2,?,xn用它们表示。
?x1?c11y1?c12y2???c1nyn?c11??x?cy?cy???cy?c21?22112222nn (并要求矩阵C?? ??????c??n1?xn?cn1y1?cn2y2???cnnyn?c1n??c22?c2n?是可逆矩阵) ?????cn2?cnn??c12
代入f?x1,x2,?,xn?,得到y1,?,yn的一个二次型g?y1,?,yn?这样的操作称为对f?x1?xn?作了一次可逆线性变量替换。
设Y??y1,y2,?,yn?,则上面的变换式可写成 T
x?CY
则f?x1?xn??xAx?YCACY?g?y1,?,yn? TTT
于是g?y1,?yn?的矩阵为CAC T
CAC?T?T?CTATCT?CTAC
实对称矩阵的合同
两个n阶实对称矩阵A和B,如果存在n阶实可逆矩阵C,值得CAC?B。称A与B合同,记作T
A~?B。
命题:二次型f?x1?xn??xAx可用可逆线性变换替换化为 T
g?y1?yn??YBY?A~?B T
二次型的标准化和规范化
1.每个二次型都可以用可逆线性变量替换化为标准二次型和规范二次型。
也就是每个实对称矩阵都会同于对角矩阵和规范对角矩阵。
设A是一个实对称矩阵,则存在正交矩阵Q,使得D?QAQ是对角矩阵。
QAQ?QAQ?D A~D,A~?D T?1?1
2.标准化和规范化的方法
①正交变换法
- 21 -
② 配方法
3.惯性定理与惯性指数
定理:一个二次型用可逆线性变换替换化出的标准形的各个平方项的系数中,大于0的个数和小于0的个数是由原二次型所决定的,分别称为原二次型的正、负惯性指数。
一个二次型化出的规范二次型在形式上是唯一的,也即相应的规范对角矩阵是唯一的。 用矩阵的语言来说:一个实对称矩阵A合同于唯一规范对角矩阵。
定理:二次型的正、负惯性指数在可逆线性变量替换下不变;两个二次型可互相转化的充要条件是它们的正、负惯性指数相等。
实对称矩阵的正(负)惯性指数就等于正(负)特征值的个数。
正定二次型与正定矩阵
定义:一个二次型f?x1,x2,?,xn?称为正定二次型,如果当x1,?,xn不全为0时,
f?x1,x2,?,xn??0。
例如,标准二次型f?x1,x2,?,xn??d1x1?d2x2???dnxn正定?di?0,i?1,?,n 222
(必要性“?”,取x1?1,x2???xx?0,此时f?1,0,?,0??d1?0同样可证每个di?0) 实对称矩阵正定即二次型xAx正定,也就是:当x?0时,xAx?0。 TT
?? 1??0 例如实对角矩阵?0??0?0? 2000??00?正定?? i?0,i?1,?,n ??0?0? n??0
定义:设A是一个n阶矩阵,记Ar是A的西北角的r阶小方阵,称Ar为A的第r个顺序主子式(或r阶顺序主子式)。
附录一 内积,正交矩阵,实对称矩阵的对角化
一.向量的内积
1.定义
两个n维实向量?,?的内积是一个数,记作??,??,规定为它们对应分量乘积之和。
?a1??b1??????a2??b2?T 设????,????,则 ??,???a1b1?a2b2???anbn ??? ???????a??b??n??n?
2.性质
①对称性:??,?????,??
- 22 -
②双线性性质:??1??2,?????1,?????2,??
??,?1??2????,?1????,?2?
?c?,???c??,?????,c??
③正交性:??,???0,且??,???0???0 ??,???
3.长度与正交
向量?的长度?ai?1n2i ??,???ai2 i?1n
?0???0 c??c
单位向量:长度为1的向量
?2????1??0??2??????, ?0?,?1?,?0??0??0??2??????????2?
若??0,则1??是单位向量,称为?的单位化。 ??1 两个向量?,?如果内积为0:??,???0,称它们是正交的。
如果n维向量组?1,?2,?,?s两两正交,并且每个都是单位向量,则称为单位正交向量组。 例1.如果向量组?1,?2,?,?s两两正交,并且每个向量都不为零向量,则它们线性无关。 证:记A?? ?1,?2,?,?s?,则
?1??0T AA???0
?0?20022000?00??0?? 0?2s??
则rAA?s,?r?A??s即r??1,?,?s??s。 T??
例2.若A是一个实的矩阵,则rAA?r?A?。 T??
二.正交矩阵
- 23 -
一个实n阶矩阵A如果满足AAT?E,就称为正交矩阵。AT?A?1 定理 A是正交矩阵?A的行向量组是单位正交向量组。
?A的列向量组是单位正交向量组。
例3.正交矩阵A保持内积,即
?A?,A?????,??
A??
证:?A?,A????TATA???T????,??
?1?
例4.(04)A是3阶正交矩阵,并且a??
11?1,求Ax??0?的解。
??0??
三.施密特正交化方法
这是把一个线性无关的向量组改造为与之等价的单位正交向量组的方法。
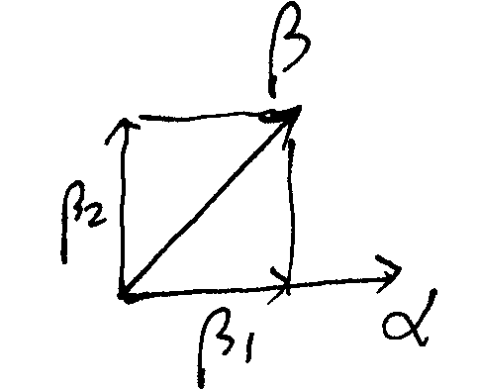
?2????1???c?
设?1,?2,?3线性无关
①正交化:令?1??1
?2??2???
1,?2?
??1
1,?1 (设?2??2?k?1,??2,?1????2,?1??k??1,?1?
当k???
2,?1?
?时,?2,?1正交。)
1,?1 ???
3??3?1,?3???,??
???23
1??2 1,1?2,?2 ②单位化:令??1?
1??,??
2?2,?3?3
1?2?3
则?1,?2,?3是与?1,?2,?3等价的单位正交向量组。
- 24 -
四.实对称矩阵的对角化
设A是一个实的对称矩阵,则
①A的每个特征值都是实数。
②对每个特征值?,重数?n?r??E?A?。即A可以对角化。
③属于不同特征值的特征向量互相正交。
于是:存在正交矩阵Q,使得QAQ是对角矩阵。
对每个特征值?,找??E?A?x?0的一个单位正交基础的解,合在一起构造正交矩阵。 设A是6阶的有3个特征值?1(二重),?2(三重),?1(一重)
找?1的2个单位正交特征向量?1,?2。
找?2的3个单位正交特征向量?3,?4,?5。
找?3的一个单位特征向量?6。
Q???1,?2,?3,?4,?5,?6?
例5.(04)A是3阶实对称矩阵,r?A??2,6是它的一个二重特征值, ?1
?1??2??1??????? ?1?,?1?和??2?都是属于6的特征向量。
?0??1??3???????
(1)求A的另一个特征值。
(2)求A。
解:(1)另一个特征值为0。
?x1??? (2)设?x2?是属于0的特征向量,则
?x??3?
?x1?x2?0? ?2x1?x2?x3?0
?x?2x?3x?023?1
此方程组n?3,r?A??2,n?r?A??1,基础解系包含一个解,任何两个解都相关。 于是,每个非零解都是属于0的特征向量。
?110??101??1??????? ?211???01?1? ????1?是一个解。
?1?23??000???1???????
- 25 -
?121??6120????? A?11?1???660? ?01?1??060?????
?110660??100422?????11266???01024?2? ?21?1?1?1000??0012?24?????
2??42?? A??24?2?
?2?24???
附录二 向量空间
1.n维向量空间及其子空间
记为R由全部n维实向量构成的集合,这是一个规定了加法和数乘这两种线性运算的集合,我们把它称为n维向量空间。
设V是R的一个子集,如果它满足
(1)当?1,?2都属于V时,?1??2也属于V。
(2)对V的每个元素?和任何实数c,c?也在V中。
则称V为R的一个子空间。
例如n元齐次方程组AX?0的全部解构成R的一个子空间,称为AX?0的解空间。
但是非齐次方程组AX?
nnnnn?的全部解则不构成Rn的子空间。 对于R中的一组元素?1,?2,?,?s,记它们的全部线性组合的集合为
L??1,?2,?,?s??c1?1?c2?2???cs?sci任意,它也是R的一个子空间。 n??
2.基,维数,坐标
设V是R的一个非0子空间(即它含有非0元素),称V的秩为其维数,记作dimV。
称V的排了次序的极大无关组为V的基。
例如AX?0的解空间的维数为n?r?A?,它的每个有序的基础解系构成基。
又如dim?L??1,?2,?,?s???r??1,?2,?,?s?,?1,?2,?,?s的每个有序的极大无关组构成基。
- 26 - n
设?1,?2,?,?k是V的一个基,则V的每个元素?都可以用?1,?2,?,?k唯一线性表示: ??c1?1?c2?2???ck?k
称其中的系数?c1,c2,?,ck?为?关于基?1,?2,?,?k的坐标,它是一个k维向量。 坐标有线性性质:
(1)两个向量和的坐标等于它们的坐标的和:
如果向量?和?关于基?1,?2,?,?k的坐标分别为?c1,c2,?,ck?和?d1,d2,?,dk?,则???关于基?1,?2,?,?k的坐标为
?c1?d1,c2?d2,?,ck?dk???c1,c2,?,ck???d1,d2,?,dk?
(2)向量的数乘的坐标等于坐标乘数:
如果向量?关于基?1,?2,?,?k的坐标为?c1,c2,?,ck?,则c?关于基?1,?2,?,?k的坐标为?cc1,cc2,?,cck??c?c1,c2,?,ck?。
坐标的意义:设V中的一个向量组?1,?2,?,?t关于基?1,?2,?,?k的坐标依次为?1,?2,?,?t,则?1,?2,?,?t和?1,?2,?,?t有相同的线性关系。
于是,我们可以用坐标来判断向量组的相关性,计算秩和极大无关组等等。
3.过渡矩阵,坐标变换公式
设?1,?2,?,?k和?1,?2,?,?k都是V的一个基,并设?1在?1,?2,?,?k中的坐标为?c1i,c2i,?,cki?,构造矩阵
?c11??c21 C?????c?k1?c1k??c22?c2k?, ?????ck2?ckk??c12
称C为?1,?2,?,?k到?1,?2,?,?k的过渡矩阵。
??1,?2,?,?k????1,?2,?,?k?C。
1 如果V中向量?在其?1,?2,?,?k和?
T,?2,?,?Tk中的坐标分别为 x??x1,x2,?,xk?和y??y1,y2,?,yk?,则
????1,?2,?,?k?x
- 27 -
????1,?2,?,?k?y???1,?2,?,?k?Cy
于是关系式:
x?Cy
称为坐标变换公式。
4.规范正交基
如果V的一基?1,?2,?,?k是单位正交向量组,则称为规范正交基。
两个向量的内积等于在规范正交基下的它们坐标的内积。
设?的坐标为?c1,c2,?,ck?,?的坐标为?d1,d2,?,dk?,
则??,???c1d1?c2d2???ckdk
两个规范正交基之间的过渡矩阵是正交矩阵。
做题思路
先化简再计算
例5.(03)设n维列向量???a,0,?,0,a?,a?0。规定A?E???,B?E?TT1??T。已知aAB?E,求a。
注意化简技巧(中间过程也很重要)
?10??01 例13.(00)己知A*??10??0?3?00100??0??1?1,求矩阵B,使得ABA?BA?3E. ?0?8??
证明一个矩阵可逆切入点 行列式=0 ,证明Ax=E ,
证明两式相等切入点 AB=某个等式=BA
(从对称性想到AB可逆BA也可逆的着手点AB?E?BA?E)
例20.设n阶矩阵A和B满足等式AB?aA?bB,ab?0, 证明:AB?BA
- 28 -
