数学极限总结
§2.1数列的极限
定义1 对于数列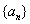 ,如果当
,如果当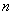 无限增大时,通项
无限增大时,通项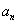 无限趋近于一个确定的常数A,则称A为数列
无限趋近于一个确定的常数A,则称A为数列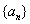 的极限,或称数列
的极限,或称数列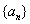 收敛于A,记作
收敛于A,记作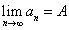 或
或 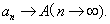
若数列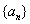 没有极限,则称该数列发散。
没有极限,则称该数列发散。
定义2(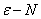 定义) 如果数列
定义) 如果数列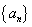 与常数A有下列关系:对于任意给定的正数
与常数A有下列关系:对于任意给定的正数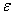 (无论它多么小)总存在正整数N,使得对于
(无论它多么小)总存在正整数N,使得对于 时的一切
时的一切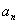 ,不等式
,不等式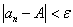 都成立,则称常数A是数列
都成立,则称常数A是数列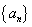 的极限。或称数列
的极限。或称数列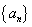 收敛于A,记为
收敛于A,记为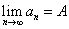 。
。
§2.2函数的极限
定义2(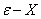 定义)如果对于任意给定的正数
定义)如果对于任意给定的正数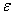 (不论它多么小),总存在着正数
(不论它多么小),总存在着正数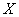 ,使得对于适合不等式
,使得对于适合不等式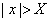 的一切
的一切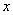 ,对应的函数值
,对应的函数值 都满足不等式
都满足不等式 ,那么常数
,那么常数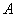 就叫做函数
就叫做函数 当
当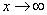 时的极限,记作
时的极限,记作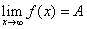 或
或 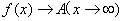 。
。
定义3(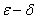 定义)如果对于任意给定的正数
定义)如果对于任意给定的正数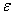 (不论它多么小),总存在着正数
(不论它多么小),总存在着正数 ,使得对于适合不等式
,使得对于适合不等式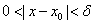 的一切
的一切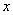 ,对应的函数值
,对应的函数值 都满足不等式
都满足不等式 ,那么常数
,那么常数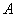 就叫做函数
就叫做函数 当
当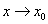 时的极限,记作
时的极限,记作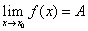 或
或 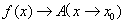 。
。
单侧极限
若函数 当自变量
当自变量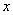 从
从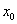 的左侧(右侧)无限趋近于
的左侧(右侧)无限趋近于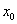 时,相应的函数值
时,相应的函数值 无限接近于一个确定的常数A,则称A为函数
无限接近于一个确定的常数A,则称A为函数 在
在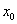 处的左(右)极限,记作
处的左(右)极限,记作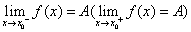 ,或
,或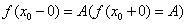 。
。
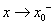 表示
表示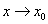 且
且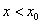 ;
;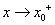 表示
表示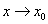 且
且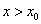 。
。
定理 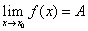 的充要条件是
的充要条件是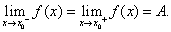
§2.3无穷小量与无穷大量
一.无穷小量
定义1 以零为极限的变量称为无穷小量,简称为无穷小。
注:(1)说一个变量是无穷小,要指明自变量的变化过程。
(2)无穷小是变量,表达的是量的变化趋势,而不是量的大小,因此,一个数不管多么小,都不是无穷小。
(3)零是唯一例外的常数中的无穷小。
2.无穷小的运算性质
定理1 有限个无穷小的代数和是无穷小。
注意,无穷多个无穷小的代数和不一定是无穷小。如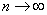 时,
时,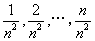 均为无穷小,但
均为无穷小,但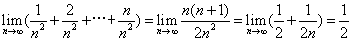
定理2 无穷小与有界量之积是无穷小。
推论1 常数与无穷小之积是无穷小。
推论2 有限个无穷小之积仍是无穷小。
…… …… 余下全文

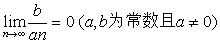 ;
;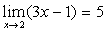 ;
; ;等等
;等等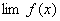 ,
,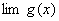 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)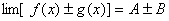
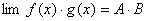
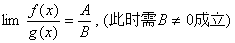
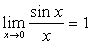
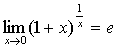 ;
; 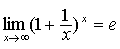
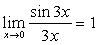 ,
,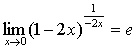 ,
,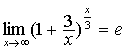 ;等等。
;等等。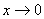 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有: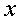 ~
~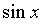 ~
~ ~
~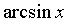 ~
~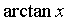 ~
~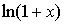 ~
~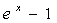 。
。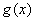 时(
时(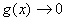 ),仍有上面的等价
),仍有上面的等价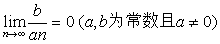 ;;;等等
;;;等等

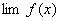 ,
, 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)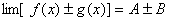
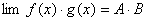
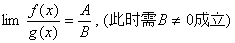
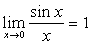
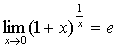 ;
; 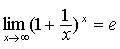
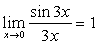 ,
,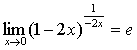 ,
, ;等等。
;等等。 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有: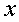 ~
~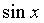 ~
~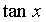 ~
~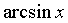 ~
~ ~
~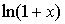 ~
~ 。
。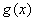 时(
时(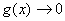 ),仍有上面的等价
),仍有上面的等价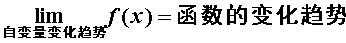
 函数的变化趋势主要有四种:
函数的变化趋势主要有四种: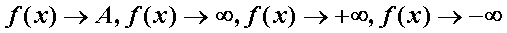
 当
当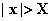 时;(
时;(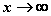 )
) 时;(
时;(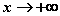 )
)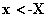 时;(
时;(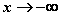 )
)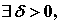 当
当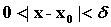 时;(
时;(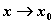 )
)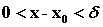 时;(
时;( )
)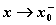 )
)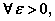
 恒时:
恒时: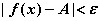 (
(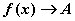 )
)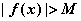 (
(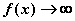 )
)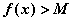 (
(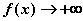 )
)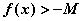 (
(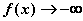 )
)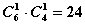 种中的任意一种。当然还有一种最特殊的函数极限,即数列的极限。它是一种自变量的变化不连续的特殊情形。
种中的任意一种。当然还有一种最特殊的函数极限,即数列的极限。它是一种自变量的变化不连续的特殊情形。