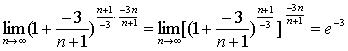极限计算方法总结
靳一东
《高等数学》是理工科院校最重要的基础课之一,极限是《高等数学》的重要组成部分。求极限方法众多,非常灵活,给函授学员的学习带来较大困难,而极限学的好坏直接关系到《高等数学》后面内容的学习。下面先对极限概念和一些结果进行总结,然后通过例题给出求极限的各种方法,以便学员更好地掌握这部分知识。
一、极限定义、运算法则和一些结果
1.定义:(各种类型的极限的严格定义参见《高等数学》函授教材,这里不一一叙述)。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如: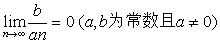 ;
;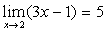 ;
; ;等等
;等等
(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 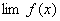 ,
,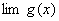 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)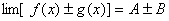
(2)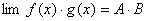
(3)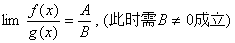
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 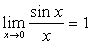
(2) 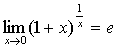 ;
; 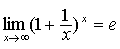
说明:不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式,
作者简介:靳一东,男,(1964—),副教授。
例如: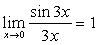 ,
,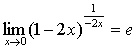 ,
,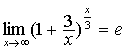 ;等等。
;等等。
4.等价无穷小
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当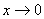 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
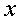 ~
~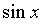 ~
~ ~
~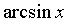 ~
~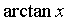 ~
~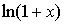 ~
~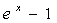 。
。
说明:当上面每个函数中的自变量x换成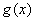 时(
时(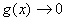 ),仍有上面的等价
),仍有上面的等价
…… …… 余下全文

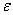 〉0,总存在一个正整数N,当n〉N时,都有
〉0,总存在一个正整数N,当n〉N时,都有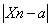 <
<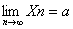 .
.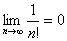 .
.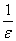 即可,
即可, ,其中
,其中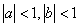 .
.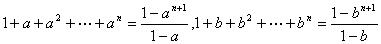 ,
,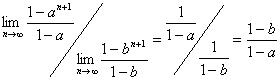 ,
, 对求极限的学习和深入研究,我总结出十二种求极限的方法.
对求极限的学习和深入研究,我总结出十二种求极限的方法. 
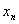 }收敛
}收敛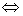
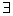 a,
a,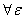 〉0,
〉0,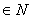
 ,当n〉N时,有
,当n〉N时,有 -a
-a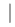 〈
〈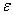 .
. 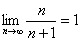
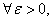 要使不等式
要使不等式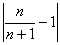 =
=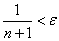 成立:解得n
成立:解得n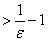 ,取N=
,取N= ,于是
,于是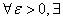 N=
N=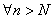 ,有
,有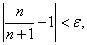 即
即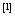
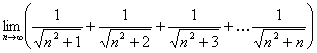
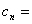
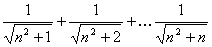

 ,于是
,于是  由
由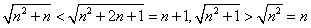 .
. 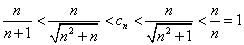
 已知:
已知: ∴
∴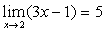

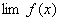 ,
,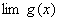 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
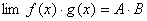


 。
。
 。
。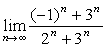
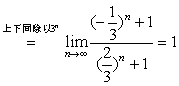 。
。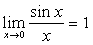
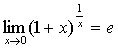 ;
; 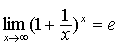
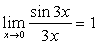 ,
,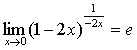 ,
,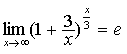 ;等等。
;等等。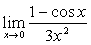
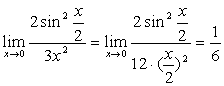 。
。
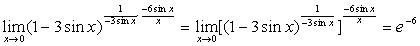 。
。