极限计算方法总结
数学是专接本公共课重要的基础课之一,极限是数学的重要组成部分。求极限方法众多,非常灵活,给函授学员的学习带来较大困难,而极限在专接本公共课数学考试中占13%-20%左右;学的好坏会关系到公共课数学的成绩。下面先对极限概念和一些结果进行总结,然后通过例题给出求极限的各种方法,以便学员更好地掌握这部分知识。
一、极限定义、运算法则和一些结果
1.定义:(各种类型的极限的严格定义参见《高等数学》函授教材,这里不一一叙述)。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如: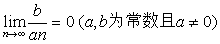 ;;;等等
;;;等等


(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 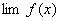 ,
, 都存在,极限值分别为A,B,则下面极限都存在,且有 (1)
都存在,极限值分别为A,B,则下面极限都存在,且有 (1)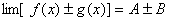
(2)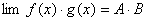
(3)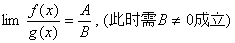
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 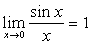
(2) 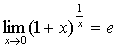 ;
; 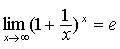
说明:不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式,
作者简介:靳一东,男,(1964—),副教授。
例如: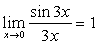 ,
,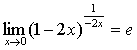 ,
, ;等等。
;等等。
4.等价无穷小
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
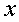 ~
~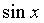 ~
~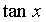 ~
~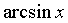 ~
~ ~
~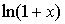 ~
~ 。
。
说明:当上面每个函数中的自变量x换成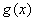 时(
时(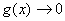 ),仍有上面的等价
),仍有上面的等价
关系成立,例如:当 时,
时, 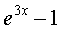 ~
~ 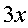 ;
;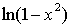 ~
~ 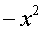 。
。
定理4 如果函数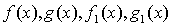 都是
都是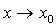 时的无穷小,且
时的无穷小,且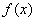 ~
~ ,
,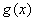 ~
~ ,则当
,则当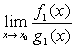 存在时,
存在时,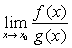 也存在且等于
也存在且等于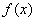
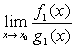 ,即
,即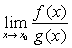 =
=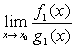 。
。
5.洛比达法则
定理5 假设当自变量x趋近于某一定值(或无穷大)时,函数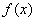 和
和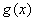 满足:(1)
满足:(1)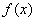 和
和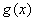 的极限都是0或都是无穷大;
的极限都是0或都是无穷大;
(2)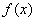 和
和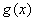 都可导,且
都可导,且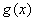 的导数不为0;
的导数不为0;
(3)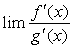 存在(或是无穷大);
存在(或是无穷大);
则极限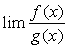 也一定存在,且等于
也一定存在,且等于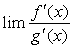 ,即
,即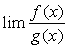 =
=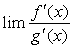 。
。
说明:定理5称为洛比达法则,用该法则求极限时,应注意条件是否满足,只要有一条不满足,洛比达法则就不能应用。特别要注意条件(1)是否满足,即验证所求极限是否为“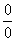 ”型或“
”型或“ ”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
”型;条件(2)一般都满足,而条件(3)则在求导完毕后可以知道是否满足。另外,洛比达法则可以连续使用,但每次使用之前都需要注意条件。
6.连续性
定理6 一切连续函数在其定义去间内的点处都连续,即如果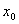 是函数
是函数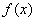 的定义去间内的一点,则有
的定义去间内的一点,则有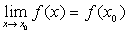 。
。
7.极限存在准则
定理7(准则1) 单调有界数列必有极限。
定理8(准则2) 已知 为三个数列,且满足:
为三个数列,且满足:
(1) 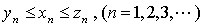
(2)  ,
,
则极限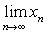 一定存在,且极限值也是a ,即
一定存在,且极限值也是a ,即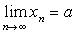 。
。
二、求极限方法举例
1. 用初等方法变形后,再利用极限运算法则求极限
例1 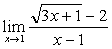
解:原式= 。
。
注:本题也可以用洛比达法则。
例2 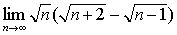
解:原式= 。
。
例3 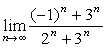
解:原式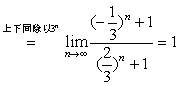 。
。
2. 利用函数的连续性(定理6)求极限
例4 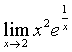
解:因为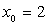 是函数
是函数 的一个连续点,
的一个连续点,
所以 原式=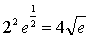 。
。
3. 利用两个重要极限求极限
例5 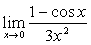
解:原式=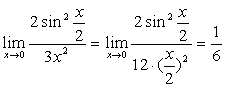 。
。
注:本题也可以用洛比达法则。
例6 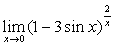
解:原式= 。
。
例7 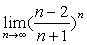
解:原式=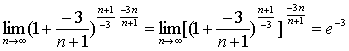 。
。
4. 利用定理2求极限
例8 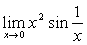
解:原式=0 (定理2的结果)。
5. 利用等价无穷小代换(定理4)求极限
例9 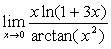
解: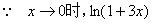 ~
~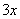 ,
,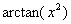 ~
~ ,
,
 原式=
原式=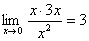 。
。
例10 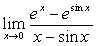
解:原式= 。
。
注:下面的解法是错误的:
原式=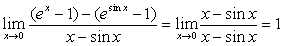 。
。
正如下面例题解法错误一样:
 。
。
例11 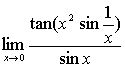
解: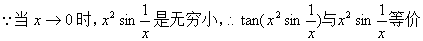 ,
,
所以, 原式=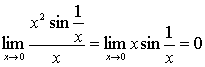 。(最后一步用到定理2)
。(最后一步用到定理2)
6. 利用洛比达法则求极限
说明:当所求极限中的函数比较复杂时,也可能用到前面的重要极限、等价无穷小代换等方法。同时,洛比达法则还可以连续使用。
例12 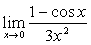 (例4)
(例4)
解:原式=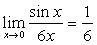 。(最后一步用到了重要极限)
。(最后一步用到了重要极限)
例13 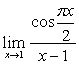
解:原式=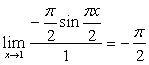 。
。
例14 
解:原式=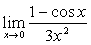 =
=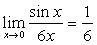 。(连续用洛比达法则,最后用重要极限)
。(连续用洛比达法则,最后用重要极限)
例15 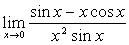
解:
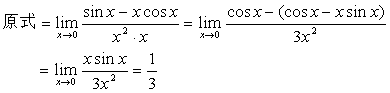
例18 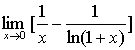
解:错误解法:原式=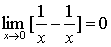 。
。
正确解法:
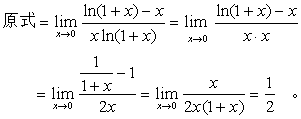
应该注意,洛比达法则并不是总可以用,如下例。
例19 
解:易见:该极限是“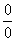 ”型,但用洛比达法则后得到:
”型,但用洛比达法则后得到: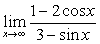 ,此极限
,此极限
不存在,而原来极限却是存在的。正确做法如下:
原式=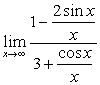 (分子、分母同时除以x)
(分子、分母同时除以x)
= (利用定理1和定理2)
(利用定理1和定理2)
7. 利用极限存在准则求极限
例20 已知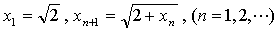 ,求
,求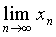
解:易证:数列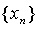 单调递增,且有界(0<
单调递增,且有界(0<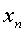 <2),由准则1极限
<2),由准则1极限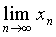 存在,设
存在,设 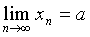 。对已知的递推公式
。对已知的递推公式  两边求极限,得:
两边求极限,得:
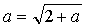 ,解得:
,解得: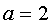 或
或 (不合题意,舍去)
(不合题意,舍去)
所以 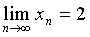 。
。
例21 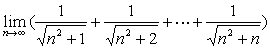
解: 易见: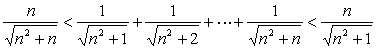
因为 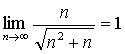 ,
,
所以由准则2得: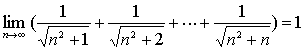 。
。
第二篇:归纳函数极限的计算方法
函数极限的计算方法
摘 要 :本文总结出了求极限的几种方法,比如用定义、公式、定理、性质求极限.
关键词:函数极限;计算方法;洛必达法则; 四则运算
The sum of the Method of Computing Function Limit
Abstract:The write sums up in this article several ways of extacting the limit by the means of definition, formula,nature, theorem and so on.
Key Words:Function Limit;Computing method;L’Hospital rules; Four fundamental rules
前言
极限的概念是高等数学中一个最基本、最重要的概念,极限理论是研究连续、导数、积分、级数等的基本工具,因此正确理解和运用极限的概念、掌握极限的求法,对学好数学分析是十分重要的.求极限的方法很多且非常灵活,本文归纳了函数极限计算的一些常见方法和技巧.
1.预备知识
1.1函数极限的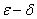 定义
定义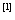
设函数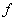 在点
在点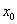 的某个空心邻域
的某个空心邻域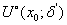 内有定义,
内有定义, 为定数,若对任给的
为定数,若对任给的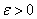 ,存在正数
,存在正数 ,使得当
,使得当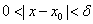 时有
时有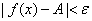 ,则称函数当趋于
,则称函数当趋于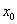 时以
时以 为极限,记作
为极限,记作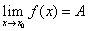 或
或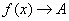
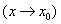 .
.
2.求函数极限的方法总结
极限是描述函数的变化趋势,以基于图形或直观结合定义可以求出一些简单的函数的极限;但是结构较为复杂的函数的图形不易画出,基于直观也就无法得出极限,本着化繁为简的思想,产生了极限的四则运算法则;由“数列的单调有界准则”和“迫敛准则”产生了两个重要极限和无穷小量的性质—有界函数与无穷小量的积仍是无穷小量;由中值定理得出了罗必达法则.以上也是我们求极限的理论依据,但在个依据下求极限又有各自的技巧.
2.1依据函数极限的迫敛性求极限
函数极限的迫敛性 设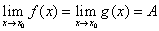 ,且在某
,且在某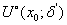 内有
内有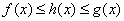 ,则
,则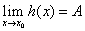 .
.
例1求极限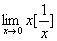
解:当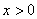 时,有
时,有
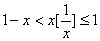
而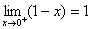 ,由函数迫敛性可得
,由函数迫敛性可得

同理可得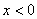 时,
时, ,即
,即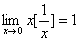
注:依据函数极限的迫敛性求极限时,需判断该函数的上下范围,这时通常用到以下不等式:
2.2 依据极限的四则运算求极限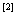
依据极限的四则运算法则求极限的题目,除了直接使用极限的四则运算法则外,往往还有以下几种类型:
分母极限为0:可先采用“约简分式”或“分子、分母有理化”进行恒等变形,将分母极限化为非零,然后再运用法则:
例2 求极限 (
(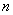 和
和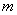 都是正整数)
都是正整数)
解:原式=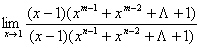
=
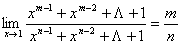
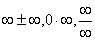 等未定型:因“
等未定型:因“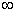 ”不是一个数,故该类型的题目不能直接使用运算法则,但可以利用“无穷大量的导数”、“分式有理化”或“通分”等方法,将其转化为极限存在后,再运用法则计算.
”不是一个数,故该类型的题目不能直接使用运算法则,但可以利用“无穷大量的导数”、“分式有理化”或“通分”等方法,将其转化为极限存在后,再运用法则计算.
例3求极限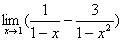
解:原式=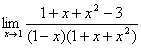
=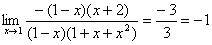
2.3 依据两个重要极限求极限
两个重要的极限: ,
, .
.
函数经过一定变形,若能出现以下情况:

时,也可采用重要极限来求.
例4 求极限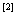

解:原式=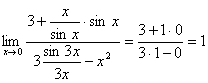
例5 求极限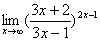
解:原式=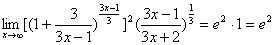
2.4依据等价无穷小替换求极限
求函数极限,若能恰当采用等价无穷小的代换,可以起到变难为易,化繁为简的作用.需要记住一些常见的等价无穷小, 如当 时:
时:
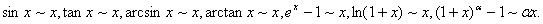
例6 求极限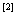
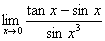
解:原式
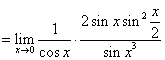
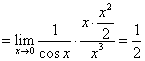
注:用等价无穷小替换求极限时,应注意只能用分子、分母整个部分去代换,或是把函数化成积的形式实行无穷小代换,对极限式的相加相减部分不能随意替代.
2.5 依据洛必达法则求极限
洛必达法则 :
:
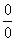 型不定式极限 若函数
型不定式极限 若函数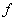 和
和 满足:
满足:
(i)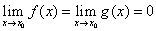 ;
;
(ii)在点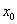 的某空心邻域
的某空心邻域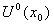 内两者都可导, 且
内两者都可导, 且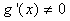
(iii)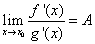 (
( 可为实数, 也可为
可为实数, 也可为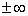 或
或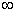 ), 则
), 则
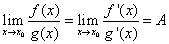
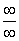 型不定式极限 若函数
型不定式极限 若函数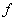 和
和 满足:
满足:
(i)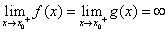 ;
;
(ii)在点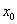 的某右邻域
的某右邻域 内两者都可导, 且
内两者都可导, 且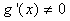
(iii)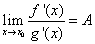 (
( 可为实数, 也可为
可为实数, 也可为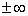 或
或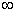 ), 则
), 则
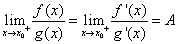
因此函数为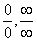 型,通常可采用此法,如下:
型,通常可采用此法,如下:
例7计算极限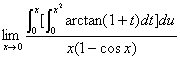
解:原式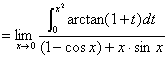
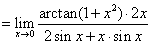
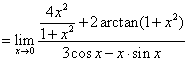
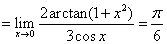
注:“洛必达法则”是求函数极限的有力工具,但在运用中,由于积、商、复合函数的求导会使分子、分母的项数增加, 导致求极限过程繁琐,因此用 法则求
法则求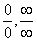 型的极限是不够的,需综合运用其它方法才能发挥作用.
型的极限是不够的,需综合运用其它方法才能发挥作用.
2.6 依据麦克劳林展开式求极限
一般常见函数的麦克劳林公式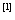 :
:
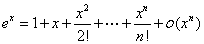
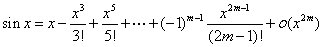
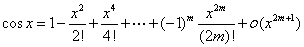
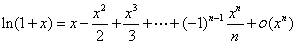
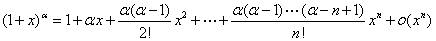
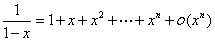
利用洛必达法则求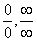 型极限时,其结果是化成某阶导数的比,而麦克劳林展开式的各项系数正分别含着各阶导数的值,因此对
型极限时,其结果是化成某阶导数的比,而麦克劳林展开式的各项系数正分别含着各阶导数的值,因此对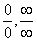 型函数极限也可采用此法.
型函数极限也可采用此法.
例8 求极限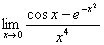
解: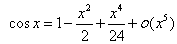
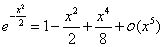
原式=
注:若本题采用洛必达法则去做,会导致计算过程繁杂.
2.7 运用函数的连续性求极限
函数的连续性定义 : 设函数
: 设函数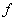 在某
在某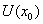 内有定义, 若
内有定义, 若
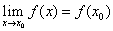 ,
,
则称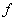 在点
在点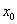 连续.
连续.
若函数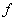 在区间
在区间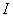 上的每一点都连续, 则称
上的每一点都连续, 则称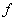 为
为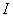 上的连续函数.
上的连续函数.
例9 计算极限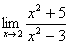
思路: 为连续函数,
为连续函数, 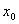 为
为 的定义区间上的一点,则
的定义区间上的一点,则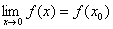 .
.
解:原式=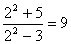
2.8 运用导数的定义求极限
导数的定义 : 设函数
: 设函数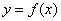 在点
在点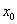 的某邻域内有定义, 若极限
的某邻域内有定义, 若极限
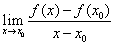
存在, 则称函数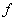 在点
在点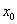 处可导, 并称该极限值为函数
处可导, 并称该极限值为函数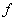 在点
在点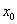 处的导数, 记作
处的导数, 记作 .
.
若函数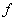 在区间
在区间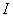 上的每一点都可导(对区间端点, 仅考虑相应的单侧导数), 则称
上的每一点都可导(对区间端点, 仅考虑相应的单侧导数), 则称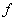 为
为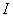 上的可导函数.
上的可导函数.
例10 计算
思路:对具有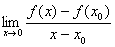 或
或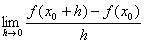 形式的极限,可由导数的定义来进行计算.
形式的极限,可由导数的定义来进行计算.
解:原式=
2.9运用定积分的定义求极限
定积分的定义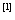 : 设
: 设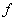 是定义在
是定义在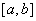 上的一个函数,
上的一个函数, 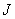 是一个确定的实数.若对任意给的正数
是一个确定的实数.若对任意给的正数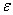 , 总存在某一正数
, 总存在某一正数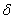 , 使得对
, 使得对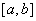 的任何分割
的任何分割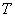 , 以及在其上任意选取的点集
, 以及在其上任意选取的点集 , 只要
, 只要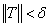 , 就有
, 就有
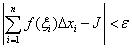
则称函数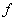 在区间
在区间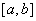 上可积或黎曼可积;数
上可积或黎曼可积;数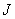 称为
称为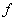 在区间
在区间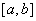 上的定积分或黎曼积分, 记作
上的定积分或黎曼积分, 记作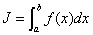
例11 计算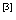

思路:和式极限,利用定积分定义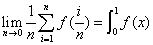
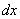 求得极限.
求得极限.
解:原式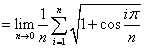

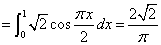
2.10 运用微分中值定理求极限
拉格朗日中值定理 : 若函数
: 若函数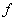 满足如下条件:
满足如下条件:
(i)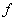 在闭区间
在闭区间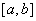 上连续;
上连续;
(ii)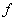 在开区间
在开区间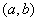 内可导,则在内至少存在一点
内可导,则在内至少存在一点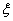 ,使得
,使得
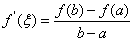 .
.
例12:计算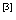
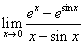
思路:对函数 在区间
在区间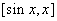 上运用拉格朗日中值定理,即可求得.
上运用拉格朗日中值定理,即可求得.
解:原式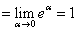 (其中
(其中 在
在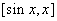 区间内)
区间内)
综上所述,求极限时,在不同的函数类型下,所采用的技巧是各不相同的,对同一题也可能有多种求法,有难有易,有时甚至需要结合上述各种方法,才能简单有效的求出,因此学会判断极限的类型和对以上的解法的灵活运用是必要的.
参考文献
[1]华东师范大学数学系. 数学分析(第五版)[M]. 高等教育出版社,2001.
[2]钱志良. 谈极限的求法[J]. 常州信息职业技术学院学报,2003.
[3]李占光. 函数极限的计算方法[J]. 长沙民政职业技术学院学报,2004.
