基本不等式知识点总结
向量不等式:
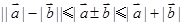
【注意】: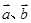 同向或有
同向或有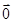
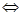
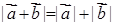
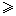
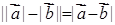 ;
;
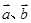 反向或有
反向或有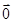
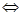
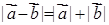
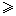
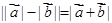 ;
;
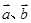 不共线
不共线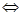
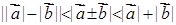 .(这些和实数集中类似)
.(这些和实数集中类似)
代数不等式:
 同号或有
同号或有
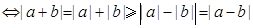 ;
;
 异号或有
异号或有
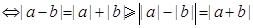 .
.
绝对值不等式: 
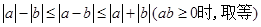
双向不等式: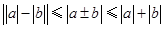
(左边当 时取得等号,右边当
时取得等号,右边当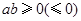 时取得等号.)
时取得等号.)
放缩不等式:
① ,则
,则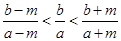 .
.
【说明】: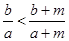 (
(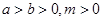 ,糖水的浓度问题).
,糖水的浓度问题).
【拓展】: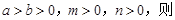
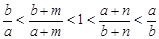 .
.
②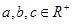 ,
,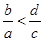 ,则
,则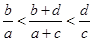 ;
;
③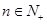 ,
,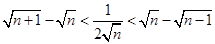 ;
;
④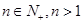 ,
,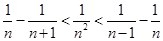 .
.
⑤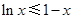
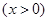 ,
,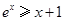
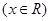 .
.
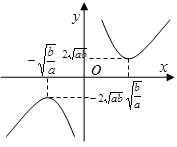 函数
函数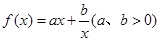 图象及性质
图象及性质
(1)函数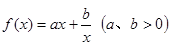 图象如图:
图象如图:
(2)函数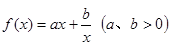 性质:
性质:
①值域: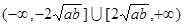 ;
;
②单调递增区间: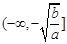 ,
,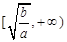 ;单调递减区间:
;单调递减区间: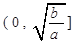 ,
,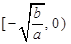 .
.
基本不等式知识点总结
重要不等式
1、和积不等式: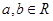
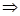
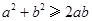 (当且仅当
(当且仅当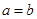 时取到“
时取到“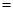 ”).
”).
【变形】:①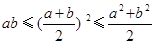 (当a = b时,
(当a = b时,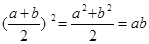 )
)
【注意】:  ,
,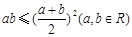
2、均值不等式:
两个正数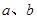 的调和平均数、几何平均数、算术平均数、均方根之间的关系,即“平方平均
的调和平均数、几何平均数、算术平均数、均方根之间的关系,即“平方平均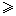 算术平均
算术平均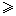 几何平均
几何平均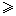 调和平均”
调和平均”
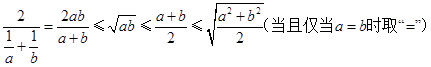
*.若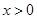 ,则
,则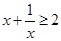 (当且仅当
(当且仅当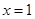 时取“=”);
时取“=”);
若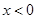 ,则
,则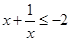 (当且仅当
(当且仅当 时取“=”)
时取“=”)
若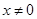 ,则
,则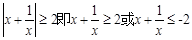 (当且仅当
(当且仅当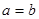 时取“=”)
时取“=”)
*.若 ,则
,则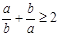 (当且仅当
(当且仅当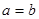 时取“=”)
时取“=”)
若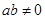 ,则
,则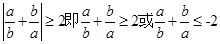 (当且仅当
(当且仅当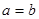 时取“=”)
时取“=”)
3、含立方的几个重要不等式(a、b、c为正数):
 (
(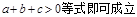 ,
, );
);
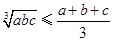
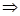
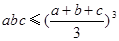
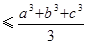
*不等式的变形在证明过程中或求最值时,有广泛应用,如:当 时,
时,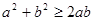 同时除以ab得
同时除以ab得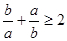 或
或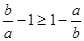 。
。
*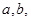 均为正数,
均为正数,
八种变式: ①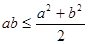 ; ②
; ②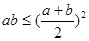 ; ③
; ③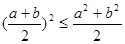
④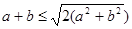 ;⑤若b>0,则
;⑤若b>0,则 ;⑥a>0,b>0,则
;⑥a>0,b>0,则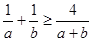 ;⑦若a>0,b>0,则
;⑦若a>0,b>0,则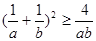 ; ⑧ 若
; ⑧ 若 ,则
,则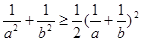 。
。
上述八个不等式中等号成立的条件都是“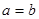 ”。
”。
最值定理
(积定和最小)
①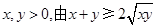 ,若积
,若积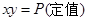 ,则当
,则当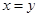 时和
时和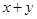 有最小值
有最小值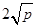 ;
;
(和定积最大)
②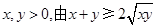 ,若和
,若和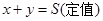 ,则当
,则当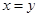 是积
是积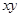 有最大值
有最大值 .
.
【推广】:已知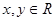 ,则有
,则有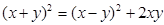 .
.
(1)若积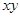 是定值,则当
是定值,则当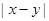 最大时,
最大时,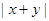 最大;当
最大;当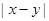 最小时,
最小时,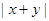 最小.
最小.
(2)若和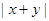 是定值,则当
是定值,则当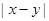 最大时,
最大时,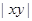 最小;当
最小;当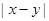 最小时,
最小时,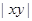 最大.
最大.
③已知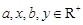 ,若
,若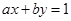 ,则有则
,则有则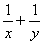 的最小值为:
的最小值为: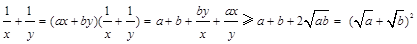
④已知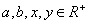 ,若
,若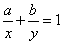 则
则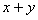 和
和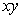 的最小值为:
的最小值为:
①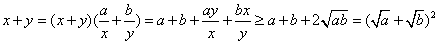 .
.
②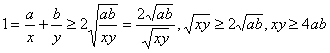
应用基本不等式求最值的“八种变形技巧”:
⑴凑系数(乘、除变量系数).例1.当 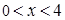 时,求函的数
时,求函的数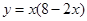 最大值.
最大值.
⑵凑项(加、减常数项):例2.已知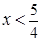 ,求函数
,求函数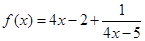 的最大值.
的最大值.
⑶调整分子:例3.求函数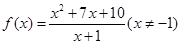 的值域;
的值域;
⑷变用公式:基本不等式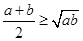 有几个常用变形,
有几个常用变形, ,
,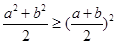 不易想到,应重视;
不易想到,应重视;
例4.求函数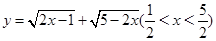 的最大值;
的最大值;
⑸连用公式:例5.已知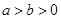 ,求
,求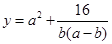 的最小值;
的最小值;
⑹对数变换:例6.已知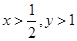 ,且
,且 ,求
,求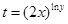 的最大值;
的最大值;
⑺三角变换:例7.已知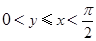 ,且
,且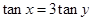 ,求
,求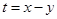 的最大值;
的最大值;
⑻常数代换(逆用条件):例8.已知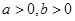 ,且
,且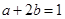 ,求
,求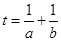 的最小值.
的最小值.
“单调性”补了“基本不等式”的漏洞:
⑴平方和为定值
若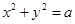 (
(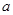 为定值,
为定值,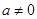 ),可设
),可设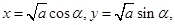 ,其中
,其中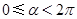 .
.
①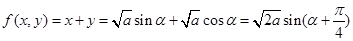 在
在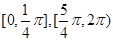 上是增函数,在
上是增函数,在 上是减函数;
上是减函数;
②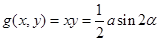 在
在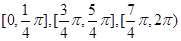 上是增函数,在
上是增函数,在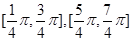 上是减函数;
上是减函数;
③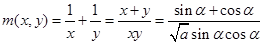 .令
.令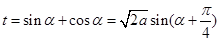 ,其中
,其中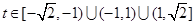 .由
.由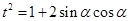 ,得
,得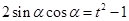 ,从而
,从而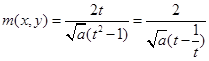 在
在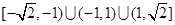 上是减函数.
上是减函数.
⑵和为定值
若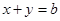 (
(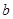 为定值,
为定值, ),则
),则
①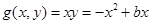 在
在 上是增函数,在
上是增函数,在 上是减函数;
上是减函数;
②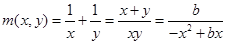 .当
.当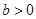 时,在
时,在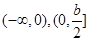 上是减函数,在
上是减函数,在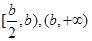 上是增函数;当
上是增函数;当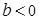 时,在
时,在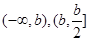 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
③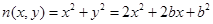 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
⑶积为定值
若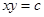 (
(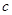 为定值,
为定值,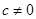 ),则
),则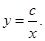
①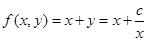 .当
.当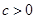 时,在
时,在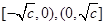 上是减函数,在
上是减函数,在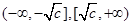 上是增函数;当
上是增函数;当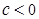 时,在
时,在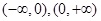 上是增函数;
上是增函数;
②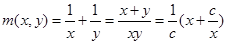 .当
.当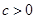 时,在
时,在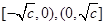 上是减函数,在
上是减函数,在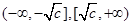 上是增函数;当
上是增函数;当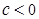 时,在
时,在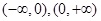 上是减函数;
上是减函数;
③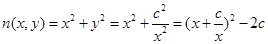 在
在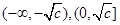 上是减函数,在
上是减函数,在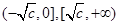 上是增函数.
上是增函数.
⑷倒数和为定值
若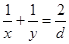 (
(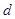 为定值,
为定值,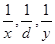 ),则
),则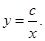 成等差数列且均不为零,可设公差为
成等差数列且均不为零,可设公差为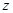 ,其中
,其中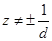 ,则
,则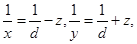 得
得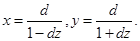 .
.
①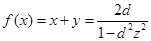 .当
.当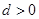 时,在
时,在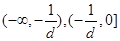 上是减函数,在
上是减函数,在 上是增函数;当
上是增函数;当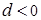 时,在
时,在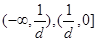 上是增函数,在
上是增函数,在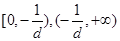 上减函数;
上减函数;
②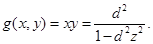 .当
.当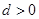 时,在
时,在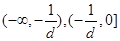 上是减函数,在
上是减函数,在 上是增函数;当
上是增函数;当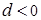 时,在
时,在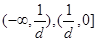 上是减函数,在
上是减函数,在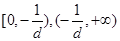 上是增函数;
上是增函数;
③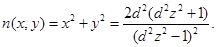 .令
.令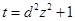 ,其中
,其中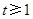 且
且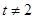 ,从而
,从而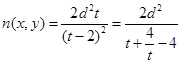 在
在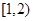 上是增函数,在
上是增函数,在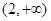 上是减函数.
上是减函数.
第二篇:不等式知识点归纳
新课标——回归教材
不等式
1、不等式的性质:
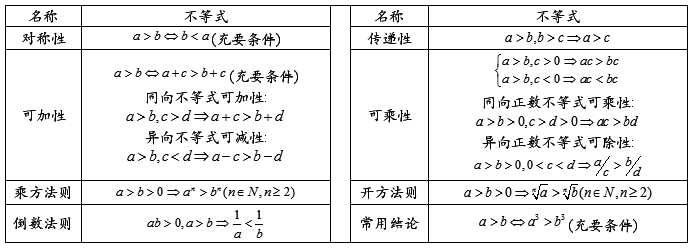
注:表中是等价关系的是解、证明不等式的依据,其它的仅仅是证明不等式的依据.
典例:1)对于实数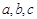 中,给出下列命题:①
中,给出下列命题:①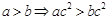 ;②
;②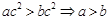 ;
;
③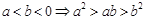 ;④
;④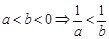 ;⑤
;⑤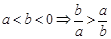 ;
;
⑥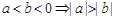 ;⑦
;⑦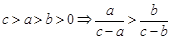 ;⑧
;⑧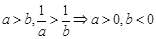 .
.
其中正确的命题是 ②③⑥⑦⑧ .
2)已知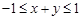 ,
, ,则
,则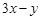 的取值范围是
的取值范围是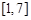 ;
;
3)已知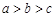 ,且
,且 则
则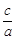 的取值范围是
的取值范围是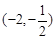 .
.
2、不等式大小比较的常用方法:
(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;
(2)作商(常用于分数指数幂的代数式);
(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;
(7)寻找中间量或放缩法;(8)图象法.其中比较法(作差、作商)是最基本的方法.
典例:1)设 ,比较
,比较 的大小
的大小
答案:①当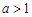 时,
时,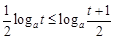 (在
(在 时取“=”);
时取“=”);
②当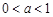 时,
时,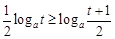 (在
(在 时取“=”);
时取“=”);
2)已知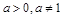 ,试比较
,试比较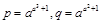 的大小.( 答:
的大小.( 答: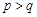 )
)
3)设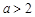 ,
,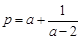 ,
,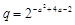 ,试比较
,试比较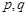 的大小(答:
的大小(答: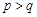 );
);
4)比较1+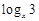 与
与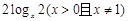 的大小.
的大小.
答:当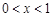 或
或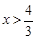 时,1+
时,1+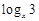 >
>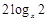 ;
;
当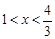 时,1+
时,1+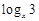 <
<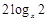 ;当
;当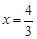 时,1+
时,1+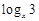 =
=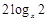
5)若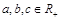 ,且
,且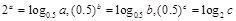 ,比较
,比较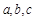 的大小.(答:
的大小.(答: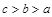 )
)
3.利用重要不等式求函数最值:“一正二定三相等,和定积最大,积定和最小”.
典例:1)下列命题中正确的是( B )
A. 的最小值是2 B.
的最小值是2 B.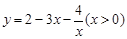 的最大值是
的最大值是
C.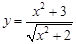 的最小值是2 D.
的最小值是2 D.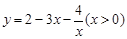 的最小值是
的最小值是 ;
;
2)若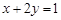 ,则
,则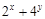 的最小值是
的最小值是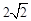 ;
;
3)已知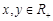 ,且
,且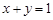 ,则
,则 的最小值为18;
的最小值为18;
变式①:已知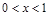 ,则
,则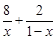 的最小值为 18 ;
的最小值为 18 ;
②:已知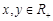 ,且
,且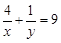 ,则
,则 的最大值为 1 ;
的最大值为 1 ;
③:已知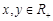 ,且
,且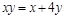 ,则
,则 的最小值为 9 ;
的最小值为 9 ;
4.常用不等式有:(1)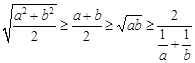
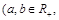 当
当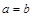 时取=号)
时取=号)
(2)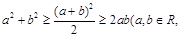 当
当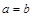 时取=号)
时取=号)
上式从左至右的结构特征为:“平方和”不小于“和平方之半”不小于“积两倍”.
(3)真分数性质定理:若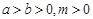 ,则
,则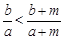 (糖水的浓度问题).
(糖水的浓度问题).
典例:若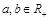 ,满足
,满足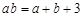 ,则
,则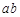 的取值范围是
的取值范围是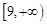 .
.
5、证明不等式的方法:比较法、分析法、综合法和放缩法.
比较法的步骤是:作差(商)后通过分解因式、配方、通分等手段变形判断符号或与1的大小,然后作出结论.)
常用的放缩技巧有: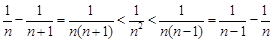 (右边当
(右边当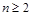 时成立)
时成立)
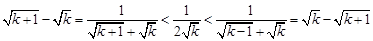
典例:1)已知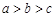 ,求证:
,求证: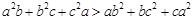 ;
;
2)已知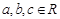 ,求证:
,求证: ;
;
3)已知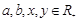 ,且
,且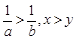 ,求证:
,求证: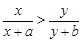 ;
;
4)若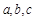 是不全相等的正数,求证:
是不全相等的正数,求证: ;
;
5)若 ,求证:
,求证: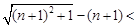
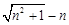 ;
;
6)求证: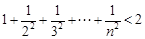 .
.
6.常系数一元二次不等式的解法:判别式-图象法
步骤:(1)化一般形式: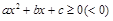 ,其中
,其中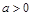 ;
;
(2)求根的情况: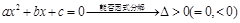 ;
;
(3)由图写解集:考虑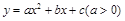 图象得解.
图象得解.
典例:解不等式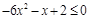 .(答:
.(答: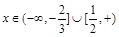 )
)
注:解一元二次不等式的过程实际上是一种函数、方程与不等式思维的转换过程,从中我们不难看出“三个二次”关系是核心,即一元二次不等式解集定值端点(非正负无穷大)是对应一元二次方程(函数)的根(零点).
典例:若关于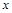 的不等式
的不等式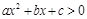 的解集为
的解集为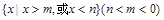 ,解关于
,解关于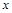 的不等式
的不等式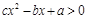 .(答:
.(答: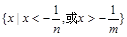 )
)
7.简单的一元高次不等式的解法:标根法:
其步骤是:(1)分解成若干个一次因式的积,并使每一个因式中最高次项的系数为正;
(2)将每一个一次因式的根标在数轴上,从最大根右上方依次通过每一点画曲线(奇穿偶回);
(3)根据曲线显现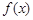 的符号变化规律,写出不等式的解集.
的符号变化规律,写出不等式的解集.
典例:1)解不等式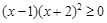 .(答:
.(答: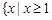 或
或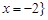 );
);
2)不等式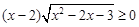 的解集是
的解集是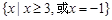 ;
;
3)设函数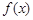 、
、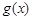 的定义域都是
的定义域都是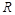 ,且
,且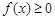 的解集为
的解集为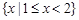 ,
,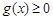 的解集为
的解集为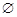 ,则不等式
,则不等式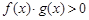 的解集为
的解集为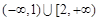 ;
;
4)要使满足关于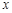 的不等式
的不等式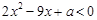 (解集非空)的每一个
(解集非空)的每一个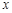 的值至少满足不等式
的值至少满足不等式 和
和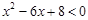 中的一个,则实数
中的一个,则实数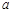 的取值范围是
的取值范围是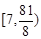 .
.
8.分式不等式的解法:
分式不等式的一般解题思路是先移项使右边为0,再通分并将分子分母分解因式,并使每一个因式中最高次项的系数为正,最后用标根法求解.解分式不等式时,一般不能去分母,但分母恒为正或恒为负时可去分母.
典例:1)解不等式 (答:
(答: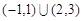 );
);
2)关于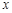 的不等式
的不等式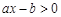 的解集为
的解集为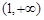 ,则关于
,则关于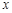 的不等式
的不等式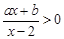 的解集为
的解集为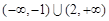 .
.
注:和一元二次不等式一样,不等式解集的端点值往往是不等式对应方程的根或不等式有意义范围的端点值.
9.绝对值不等式的解法:(了解)
(1)分域讨论法(最后结果应取各段的并集)
典例:解不等式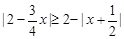 ;(答:
;(答: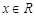 );
);
(3)利用绝对值的定义;(3)数形结合;
典例:解不等式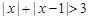 ;(答:
;(答: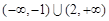 )
)
(4)两边平方
典例:若不等式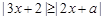 对
对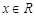 恒成立,则实数
恒成立,则实数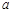 的取值范围为
的取值范围为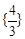
10、含参不等式的解法:通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”
注意:①解完之后要写上:“综上,原不等式的解集是…”.
②按参数讨论,最后应按参数取值分别说明其解集;但若按未知数讨论,最后应求并集.
典例:1)若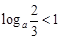 ,则
,则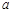 的取值范围是
的取值范围是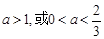 ;
;
2)解不等式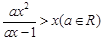 .
.
(答: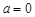 时,
时,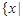
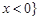 ;
; 时,
时, 或
或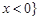 ;
;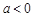 时,
时, 或
或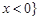 )
)
含参数的一元二次不等式的解法:三级讨论法.
一般地,设关于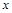 的含参数
的含参数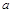 的一元二次形式的不等式为:
的一元二次形式的不等式为: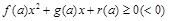 .
.
(1)第一级讨论:讨论二次项系数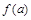 是否为零;
是否为零;
(2)第二级讨论:若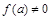 时,先观察其左边能否因式分解,否则讨论
时,先观察其左边能否因式分解,否则讨论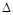 的符号;
的符号;
(3)第三级讨论:若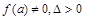 时,先观察两根
时,先观察两根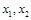 大小是否确定,否则讨论两根的大小.
大小是否确定,否则讨论两根的大小.
注意:每一级的讨论中,都有三种情况可能出现,即“>”,“=”,“<”,应做到不重不漏.
典例:1)解关于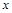 的不等式
的不等式 .
.
答:①当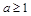 时,
时,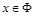 ;②当
;②当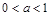 时,
时,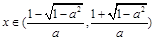 ;
;
③当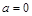 时,
时, ;④当
;④当 时,
时,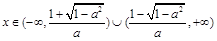
⑤当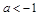 时,
时,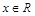
2)解关于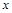 的不等式
的不等式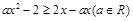 .
.
答:①当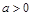 时,
时,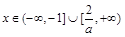 ;②当
;②当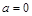 时,
时,
③当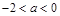 时,
时,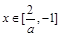 ;④当
;④当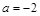 时,
时,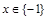 ;⑤当
;⑤当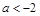 时,
时,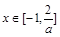
提醒:解不等式是求不等式的解集,最后务必有集合的形式表示.
11.不等式的恒成立、能成立、恰成立等问题:不等式恒成立问题的常规处理方式?
常应用函数方程思想和“分离变量法”转化为最值问题,也可抓住所给不等式的结构特征,利用数形结合法.
1).恒成立问题★★★
若不等式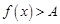 在区间
在区间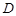 上恒成立,则等价于在区间
上恒成立,则等价于在区间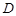 上
上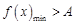
若不等式 在区间
在区间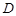 上恒成立,则等价于在区间
上恒成立,则等价于在区间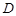 上
上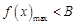
典例:1)设实数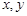 满足
满足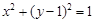 ,当
,当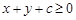 时,
时,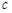 的取值范围是
的取值范围是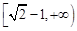 ;
;
2)不等式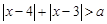 对一切实数
对一切实数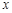 恒成立,求实数
恒成立,求实数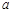 的取值范围
的取值范围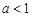 ;
;
3)若 对满足
对满足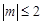 的所有
的所有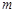 都成立,则
都成立,则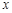 的取值范围
的取值范围 ;
;
4)若不等式 对于任意正整数
对于任意正整数 恒成立,则实数
恒成立,则实数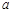 的取值范围是
的取值范围是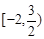
5)若不等式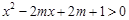 对
对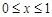 恒成立,则
恒成立,则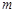 的取值范围
的取值范围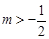
2).能成立问题
若在区间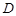 上存在实数
上存在实数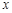 使不等式
使不等式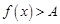 成立,则等价于在区间
成立,则等价于在区间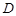 上
上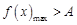 ;
;
若在区间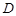 上存在实数
上存在实数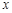 使不等式
使不等式 成立,则等价于在区间
成立,则等价于在区间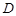 上的
上的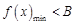 .
.
注意:若方程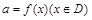 有解,则等价于
有解,则等价于
典例:1)已知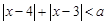 在实数集
在实数集 上的解集不是空集,求实数
上的解集不是空集,求实数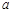 的取值范围
的取值范围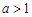
2)已知 函数
函数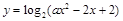 的定义域为
的定义域为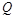 .
.
①若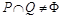 ,求实数
,求实数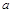 的取值范围.(答:
的取值范围.(答: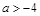 )
)
②若方程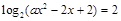 在
在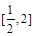 内有解,求实数的取值范围.(答:
内有解,求实数的取值范围.(答: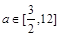 )
)
3).恰成立问题
若不等式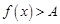 在区间
在区间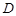 上恰成立,则等价于不等式
上恰成立,则等价于不等式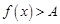 的解集为
的解集为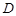 ;
;
若不等式 在区间
在区间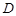 上恰成立,则等价于不等式
上恰成立,则等价于不等式 的解集为
的解集为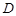 .
.
12..简单的线性规划问题:
(1)二元一次不等式(组)表示平面区域
①一般地,二元一次不等式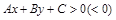 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线 某一侧的所有点组成的平面区域(半平面)不含边界线;
某一侧的所有点组成的平面区域(半平面)不含边界线;
