高数积分总结
一、不定积分
1、不定积分的概念也性质
定义1:如果在区间I上,可导函数F(x)的导函数为f(x),即对任一x?I,都有
F`(x)=f(x)或dF(x)=f(x)dx,
那么函数F(x)就称为f(x)(或f(x)dx)在区间I上的原函数。
定义2:在区间I上,函数f(x)的带有任意常数项的原函数称为f(x)(或者f(x)dx)在区间I上的不定积分,记作
?f(x)dx。
性质1:设函数f(x)及g(x)的原函数存在,则
?[f(x)?g(x)]dx??f(x)dx??g(x)dx。
性质2:设函数f(x)的原函数存在,k为非零常数,则
?kf(x)dx?k?f(x)dx。
2、换元积分法
(1)第一类换元法:
定理1:设f(u)具有原函数,???(x)可导,则有换元公式
?f[?(x)]?'(x)dx?[?f(?)d?]??
?(x)。
例:求?2cos2xdx
解 ?2cos2xdx??cos2x?2dx??cos2x?(2x)'dx??cos?d? 将??2x代入,既得
?2cos2xdx?sin2x?C
(2)第二类换元法:
定理2:设x??(t)是单调的、可导的函数,并且?'(t)?0.又设f[?(t)]?'(t)具有原函数,则有换元公式
?f(x)dx?[?f[?(t)]?'(t)dt]
?1其中?(x)是x??(t)的反函数。 t???1(x),
例:求?dx
x?a22(a?0)
22解 ∵1?tant?sect, ????设x??tant???t??,那么 2??2
x2?a2?a2?a2tan2t?a?tan2t?asect,dx?asec2tdt, 于是
?asec2t??dt??sectdt 22asectx?adx
∴?
∵sect?
∴?dxdxx?a22?lnsect?tant?C x2?a2,且sect?tant?0 a???C?ln(x?x2?a2)?C,C?C?lna 11??22?xx?a?ln???aax2?a2?
3、分部积分法
定义:设函数???(x)及???(x)具有连续导数。那么,两个函数乘积的导数公式为
????'??'????'
移项得 ??'?(??)'??'? 对这个等式两边求不定积分,得
???'dx??????'?dx
此公式为分部积分公式。
例:求?xcosxdx
解 ?xcosxdx?xsinx??sinxdx
∴xcosxdx?xsinx?cosx?C ?
分部积分的顺序:反对幂三指。
4、有理函数的积分 例:求?x?1dx 2x?5x?6
2解 ∵x?5x?6?(x?3)(x?2),故设
x?1AB?? x2?5x?6x?3x?2
其中A,B为待定系数。上式两端去分母后,得
x?1?A(x?2)?B(x?3)
即 x?1?(A?B)x?2A?3B 比较上式两端同次幂的系数,既有
?A?B?1 ??2A?3B??1
从而解得 A?4,B??3
于是
x?13??4??dx?4lnx?3?3lnx?2?C ?x2?5x?6dx????x?3x?2?
其他有些函数可以化做有理函数。
5、积分表的查询
二、定积分
1、定积分的定义和性质
(1)定义:设函数f(x)在?a,b?上有界,在?a,b?中任意插入若干个分点
a?x0?x1?x2???xn?1?xn?b
把区间?a,b?分成n个小区间
?x0,x1?,?x1,x2?,?,?xn?1,xn?
各个小区间的长度依次为
?x1?x1?x0,?x2?x2?x1,?,?xn?xn?xn?1
在每个小区间?xi?1,xi?上任取一点?i?xi?1??i?xi?,作函数值f(?i)与小区间长度?xi的乘积f(?i)?xi?i?1,2,?,n?,并作出和
S??f(?i)?xi i?1n
记??max??x1,?x2,?,?xn?,如果不论对?a,b?怎么划分,也不论在小区间xi?1,xi上点?i怎么选取,只要当??0时,和S总趋于确定??
的极限I,那么称这个极限I为函数
(简称积分),记作f(x)在区间?a,b?上的定积分?b
af(x)dx,即
n?
其中
变量,baf(x)dx?I?lim?f(?i)?xi ??0i?1f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分a叫做积分下限,b叫做积分上限,?a,b?叫做积分区间。
f(x)在区间?a,b?上有界,且只有有限个间断点,则f(x)定理1:设f(x)在区间?a,b?上连续,则f(x)在?a,b?上可积。 定理2:设
在?a,b?上可积。
(2)性质1:
性质2:??f(x)?g(x)?dx??abbaf(x)dx??g(x)dx ab?kf(x)dx?k?abbaf(x)dx (k是常数)
性质3:设a?c?b,则
?b
af(x)dx??f(x)dx??f(x)dx accb
性质4:如果在区间?a,b?上f(x)?1,则
?1dx??dx?b?a aabb
性质5:如果在区间?a,b?上,f(x)?0,则
?
?b
abaf(x)dx?0?a?b? 推论1:如果在区间?a,b?上,f(x)?g(x),则 f(x)dx??g(x)dx?a?b? ab
推论2: ?b
af(x)dx??f(x)dx(a?b) ab
性质6:设M及m分别是函数
最小值,则 f(x)在区间?a,b?上的最大值和
m(b?a)??f(x)dx?M(b?a)(a?b) ab
性质7(定积分中值定理):如果函数f(x)在积分区间?a,b?上连续,则在?a,b?上至少存在一个点?,使下式成立
?b
af(x)dx?f(?)(b?a)(a???b)
2、微积分基本公式
(1)积分上限函数及其导数
定理1:如果函数f(x)在区间?a,b?上连续,则积分上限的函数
??x???f(t)dt ax
在?a,b?上可导,并且它的导数
dx?'(x)?f(t)dt?f(x)(a?x?b) ?adx
定理2:如果函数f(x)在区间?a,b?上连续,则函数
?(x)??f(t)dt ax
就是f(x)在区间?a,b?上的一个原函数。
f(x)在区间?a,b?上的一个原函(2)牛顿-莱布尼茨公式 定理3:如果函数F(x)是连续函数
数,则
?
(1)定积分的换元法 定理:
三、多元函数微分
四、重积分
五、曲面和曲线积分 baf(x)dx?F(b)?F(a) 3、定积分的换元法和分部积分法
第二篇:高等数学一-微积分总结
 导数
导数
微分学
微分
微积分
不定积分
积分学
定积分
无穷级数
第一章函数及其特性
1.1 集合
一、定义:由具有共同特性的个体(元素)组成。
 二、表达方式: 集合A,B,C……(大写字母)
二、表达方式: 集合A,B,C……(大写字母)
元素a,b,c……(小写字母)
A={a,b,c}
元素的排列无重复,无顺序。
 a属于A记作a
a属于A记作a A,1不属于A记作1
A,1不属于A记作1 A或1
A或1 A
A
 三、分类 有限集
三、分类 有限集
无限集
空集Ф
四、集合的运算
1、子集:存在A、B两个集合,如果A中所有元素都在B中,则A叫做B的子集,A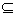 B或B
B或B A(空集是任何集合的子集)。
A(空集是任何集合的子集)。
2、交集: 存在A、B两个集合,由既在A中又在B中的元素组成的集合。A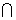 B,A
B,A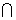 B
B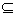 A,A
A,A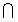 B
B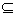 B,Ф
B,Ф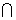 B=Ф(空集与任何集合的交集是Ф)。
B=Ф(空集与任何集合的交集是Ф)。
3、并集:存在A、B两个集合,由所有在A、B中的元素组成的集合。A B,A
B,A B
B A,A
A,A B
B B,Ф
B,Ф B=B。
B=B。
4、补集:存在A、B两个集合,且A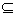 B,由在B当中但不在A中的元素组成的集合,叫A的补集,B叫全集。记作AB或
B,由在B当中但不在A中的元素组成的集合,叫A的补集,B叫全集。记作AB或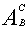 , AB
, AB A=Ф, AB
A=Ф, AB  A=B
A=B


 五、数、数轴、区间、邻域
五、数、数轴、区间、邻域
 1、数 实数
1、数 实数
虚数: 规定i2= -1,i叫虚数单位,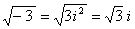
2、数轴:规定了原点、正方向和单位长度的直线。
3、区间
(1)闭区间a≤x≤b,x [a, b]
[a, b]
(2)开区间a< x< b, x (a, b)
(a, b)
 (3)半开区间 a≤x< b, x
(3)半开区间 a≤x< b, x [a, b)
[a, b)
a< x≤b, x (a, b]
(a, b]
 (4)无限区间 x≤a, x
(4)无限区间 x≤a, x (-∞, a]
(-∞, a]
x≥b, x [ b, +∞)
[ b, +∞)
x R, x
R, x (-∞, +∞)
(-∞, +∞)

 4、邻域:以
x = x0为圆心,以
δ
> 0(
δ为非常小的正数)为半径作圆,与数轴相交于A、B两点,
x0 -
δ
< x0 < x0 +
δ叫x
0的δ邻域。
4、邻域:以
x = x0为圆心,以
δ
> 0(
δ为非常小的正数)为半径作圆,与数轴相交于A、B两点,
x0 -
δ
< x0 < x0 +
δ叫x
0的δ邻域。

 例1 已知A={x
例1 已知A={x -2≤x< 3},B={x
-2≤x< 3},B={x -1< x≤5},求A
-1< x≤5},求A B, A
B, A B
B
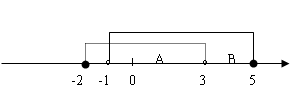 解:A、B集合中x的取值范围在数轴表示如下
解:A、B集合中x的取值范围在数轴表示如下

 所以A
所以A B={x
B={x -1< x< 3}, A
-1< x< 3}, A B={x
B={x -2≤x≤5}
-2≤x≤5}
例2 已知A、B为两非空集合,则A B=A是A=B的[ (2) ]
B=A是A=B的[ (2) ]
(1)充分条件 (2)充分必要条件 (3)必要条件 (4)无关条件
注:如果A成立,那么B成立,即“A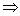 B”,那么条件A是B成立的充分条件;如要使B成立,必须有条件A,但只有A不一定能使B成立,则称A是B成立的必要条件;如果“A
B”,那么条件A是B成立的充分条件;如要使B成立,必须有条件A,但只有A不一定能使B成立,则称A是B成立的必要条件;如果“A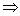 B”,又有“B
B”,又有“B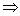 A”,则称条件A是B成立的充分必要条件。
A”,则称条件A是B成立的充分必要条件。
例3 已知集合M={0,1,2},则下列写法正确的是[ D ]
A、 {1} M B、 1
M B、 1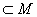 C、 1
C、 1 M D、{1}
M D、{1}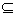 M
M
1.2 函数及其几何特性
一、定义:在一过程中,存在两个变量x、y,y是按照某一对应规则f随x的变化而变化,y就叫做关于x的函数(一元函数),表达式:y=f (x)
x叫自变量,定义域Df (x取值范围)
y叫因变量,值域DR (y取值范围)
二、求定义域
例1 求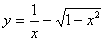 的定义域。
的定义域。
解: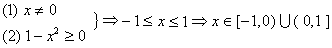
例2 求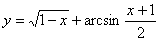 的定义域
的定义域
解: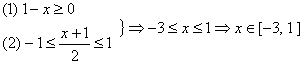
例3 求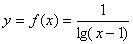 的定义域
的定义域
解: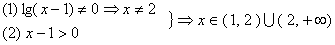
注:真数等于1时,对数值等于0。
三、图象
四、几何特性
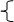 1、单调性。对于y=f(x), x
1、单调性。对于y=f(x), x Df, if y随x的增加而增加,则y=f(x)在Df内单调增。
Df, if y随x的增加而增加,则y=f(x)在Df内单调增。
y随x的增加而减少,则y=f(x)在Df内单调减。
2、有界性。对于y=f(x), x Df, 对于任一x
Df, 对于任一x Df,满足A≤f(x)≤B,则y=f(x)在Df内有界,A叫下界,B叫上界。
Df,满足A≤f(x)≤B,则y=f(x)在Df内有界,A叫下界,B叫上界。
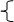 3、奇偶性。对于y=f(x), x
3、奇偶性。对于y=f(x), x Df, 且Df为对称区间, if f(-x)=f(x),则y=f(x)为偶函数。
Df, 且Df为对称区间, if f(-x)=f(x),则y=f(x)为偶函数。
f(-x)= -f(x),则y=f(x)为奇函数。
如两者均不符合,则y=f(x)为非奇非偶函数。
注:偶函数的图象关于y轴对称,奇函数的图象关于原点对称。
4、周期性。(三角函数的周期性)
对于y=f(x), x Df, if 存在T>0,满足f(x+T)=f(x), 则y=f(x)是周期函数,T叫最小正周期。
Df, if 存在T>0,满足f(x+T)=f(x), 则y=f(x)是周期函数,T叫最小正周期。
例1 讨论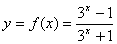 的奇偶性(x
的奇偶性(x R)
R)
解: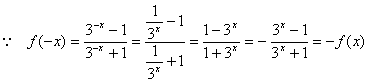
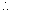 原函数是奇函数
原函数是奇函数
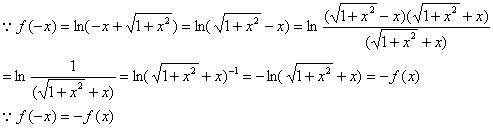 例2 讨论
例2 讨论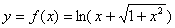 的奇偶性(x
的奇偶性(x R)。
R)。
解:
 原函数是奇函数
原函数是奇函数
1.3 五种基本的初等函数
一、幂函数
1、形如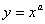 ,a为常数。
,a为常数。
2、幂函数的定义域、值域、几何特性依a的取值而定。
如a取以下值:

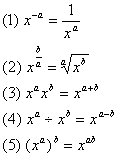 3、运算法则
3、运算法则
(a, b为正整数)
二、指数函数
1、形如 且
且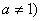
2、x R,y>0
R,y>0
3、当x=0时,y=1,则图象一定过点(0,1)
 4、几何特性。单调性 0<a<1 单调减
4、几何特性。单调性 0<a<1 单调减
a>1 单调增
 5、图象
5、图象
6、运算法则(同幂函数)
三、对数函数
1、形如 且
且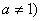
2、x>0,y R
R
3、当x=1时,y=0,则图象一定过点(0,1)
当x=a时,y=1
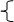 4、几何特性。单调性 0<a<1 单调减
4、几何特性。单调性 0<a<1 单调减
a>1 单调增
 5、图象
5、图象
6、两种特殊的对数
(1)当a=10时,y=log10x=lgx(常用对数)
(2) 当a=e时,y=logex=lnx(自然对数,e≈2.718)
7、运算法则
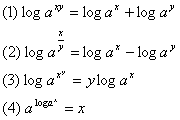
四、三角函数(掌握其几何特性、特殊三角函数的图象、基本运算)
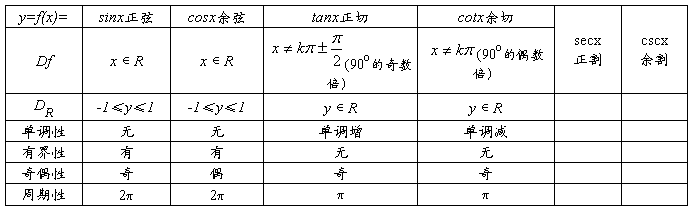
特殊角的三角函数值

图象:
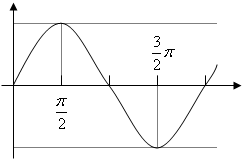
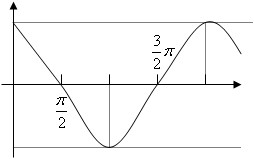 sinx cosx
sinx cosx
1 1
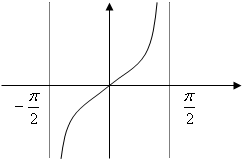 -1 -1
-1 -1
tanx
常用公式:

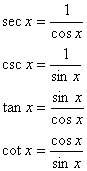
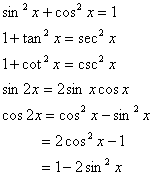
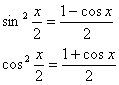
两种特殊的三角形式求周期:
(1) y=Asin(ωx+θ), 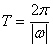
(2) y=|sinx|, T=π
五、反三角函数

图象:
arctanx arccotx
arccotx
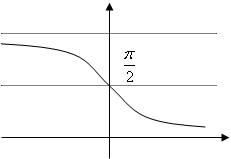 π
π
-
通过以上五种基本函数有限次的加、减、乘、除、乘方、开方、复合,就构成了初等函数。
1.4 复合函数、反函数、分段函数
一、复合函数
由y=f(u), u=g(x), 可得到y=f [g(x)],叫做y关于x的复合函数,u叫中间变量。
例1 已知 , 求f(x). 例2 已知f(x+1)=x(x-1), 求f(x)
, 求f(x). 例2 已知f(x+1)=x(x-1), 求f(x)
解:设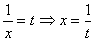 解:令t=x+1, 则x=t-1
解:令t=x+1, 则x=t-1


注:t和x都是代表变量,习惯性用x表示自变量,因此最后答案直接用x代替t.
例3 已知f(x-1)=x2+x+1, 求 例4 已知f(x)的定义域为[0, 4],求f(x2)的解:令t=x-1, 则x=t+1 定义域。
例4 已知f(x)的定义域为[0, 4],求f(x2)的解:令t=x-1, 则x=t+1 定义域。

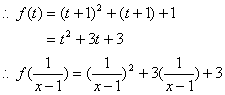

例5 已知f(x+2)=x2-2x+3, 求f [f(2)].
解法①:令t=x+2, 则x=t-2 解法②:由f(2)可知f(x+2)中x=0
f(t)=(t-2)2-2(t-2)+3=t2-6t+11 ∴ f(2)=02-2×0+3=3
则f(2)=22-6×2+11=3 则由f [f(2)]=f(3)又可知x=1
所以f [f(2)]=f(3)=32-6×3+11=2 ∴ f [f(2)]= f(3)= 12-2×1+3=2
二、反函数
已知y=f(x)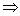 x=F(y)即y=F(x), 则y=F(x)叫y=f(x)的反函数,可记作f -1(x).
x=F(y)即y=F(x), 则y=F(x)叫y=f(x)的反函数,可记作f -1(x).
1、反函数与原函数的图象关于直线y=x对称。
2、两组反函数
(1) y=ax与y=logax, 指数函数与对数函数互为反函数。

(2) y=sinx与 y=arcsinx (- ≤x≤
≤x≤ )
)
 例:求
例:求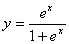 的反函数。
的反函数。
解:由原函数可得
即反函数为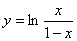
三、分段函数(关键在分段点)
1.5 几种简单经济函数的建立
价格P,需求量D,产量Q,总收益R,总成本C,总利润L
本书中设定需求量与产量为理想状态的关系,即D=Q
一、需求函数:D=D(P)
二、总收益函数: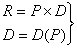
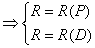
三、总成本函数:C=变动成本+固定成本
四、总利润函数:L=R-C
例:已知需求函数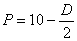 ,求R(P), R(D).
,求R(P), R(D).
解: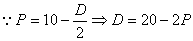
R=P×D=P×(20-2P)=-2P2+20P
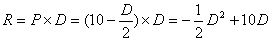
∴R(P)= -2P2+20P
R(D)= 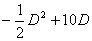
第二章函数的极限、连续性
2.1 函数的极限
一、数列的极限
1、数列:按自然数的顺序排列的一列数,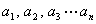 .
. 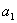 首项,
首项,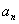 通项公式。
通项公式。
2、数列的极限:对于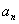 ,当n→(趋向于)∞时,if
,当n→(趋向于)∞时,if 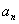 →A, 则A叫
→A, 则A叫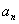 当n→∞时的极限。
当n→∞时的极限。
记作: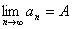
二、函数的极限
1、对于y=f(x), 当x→∞时,if f(x) →A, 则A叫f(x)当x→∞时的极限,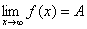
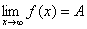 的充分必要条件:
的充分必要条件:
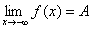 ,即左右极限存在且相等。
,即左右极限存在且相等。
例:判断 是否存在。
是否存在。
解:由arctanx的图象可知
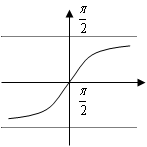 当x→-∞时,
当x→-∞时,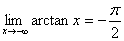
当x→+∞时,
所以 不存在。
不存在。
2、对于y=f(x), 当x→xo时, if f(x) →B, 则B叫做f(x)当x→xo时的极限,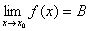
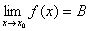 的充分必要条件:
的充分必要条件: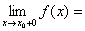
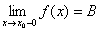 ,即左右极限存在且相等。
,即左右极限存在且相等。
例1 已知 ,判断
,判断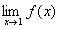 是否存在。
是否存在。
解:
∴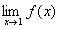 存在
存在
例2 判断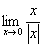 是否存在。
是否存在。
解: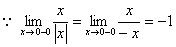
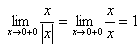
∴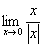 不存在
不存在
三、函数的极限的计算
1、运算法则:已知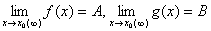

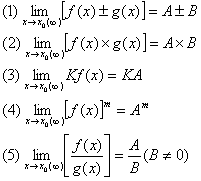 (K是常数)
(K是常数)
2、判别法则
(1)夹逼准则:在xo的邻域存在f(x), g(x), w(x),且g(x)≤f(x)≤w(x)
if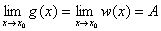 , 则
, 则
(2)单调有界函数必有极限
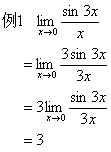
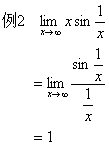

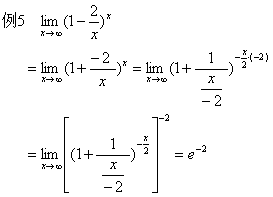
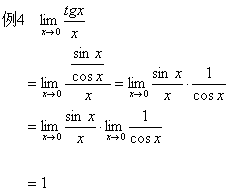


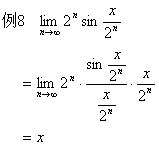
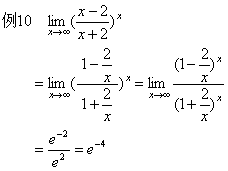
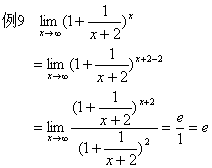
三、一般初等函数求极限
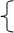 1、当x→xo时,if f(x)在xo有意义,则极限等于f(xo).
1、当x→xo时,if f(x)在xo有意义,则极限等于f(xo).
f(x)在xo无意义,则对f(x)进行恒等变换,将f(x)变换为在xo有意义或公式的形式。
2、当x→∞时,利用公式或利用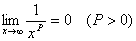 来求极限。
来求极限。
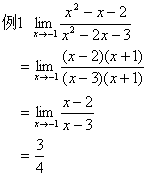
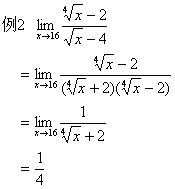
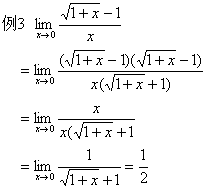

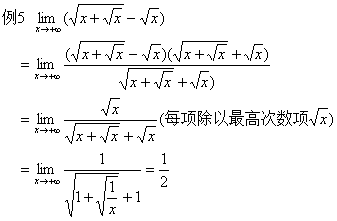

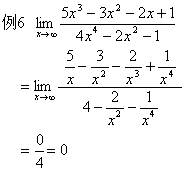
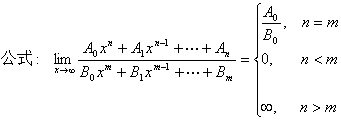
四、分段函数求极限(以x→xo为例)
1、如果xo不是分段点,则按初等函数定。
2、如果xo是分段点,则利用充分必要条件。
例1 已知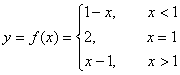 ,求
,求
解:(1) 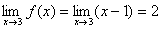
(2) 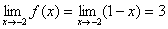
(3) 当x→1时,1为分段点,利用左右极限存在且相等的充分必要条件:
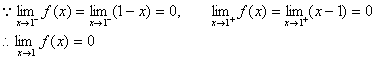
例2 已知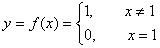 ,求
,求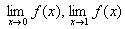
解: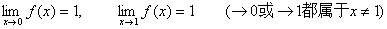
2.2 无穷大量、无穷小量
一、定义:对于y=f(x), 当x→xo(x→∞)时
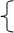 if f(x)→∞, 则称f(x)是当x→xo(x→∞)时的无穷大量。
if f(x)→∞, 则称f(x)是当x→xo(x→∞)时的无穷大量。
if f(x)→0, 则称f(x)是当x→xo(x→∞)时的无穷小量。
注:当x→0时,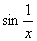 既不是无穷大量,也不是无穷小量,是一个有界函数。
既不是无穷大量,也不是无穷小量,是一个有界函数。
当x→∞时,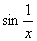 是无穷小量。
是无穷小量。
二、两者间的关系:当x在同一变化趋势下时,两者互为倒数。
已知当x→xo时,如果f(x)→∞(0),则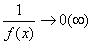
三、无穷小量的性质
1、有限个无穷小量的和、差、积仍是无穷小量。
2、无穷小量与有界函数的积,仍为无穷小量。
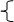 三角函数的角度 →0时,用公式来求极限。
三角函数的角度 →0时,用公式来求极限。
→∞时,把三角函数当成有界函数,配无穷小量来求极限。

3、如果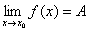 , 则在xo的邻域内f(x)-A=ω(x)(无穷小量),即f(x)与A之间相差一个无穷小量。
, 则在xo的邻域内f(x)-A=ω(x)(无穷小量),即f(x)与A之间相差一个无穷小量。
四、无穷小量的阶次的比较
已知x→xo(x→∞)时,f(x)→0, g(x)→0, 取

例1 当x→0时,比较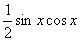 与x的阶次。
与x的阶次。
解: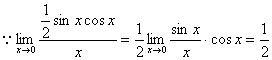
∴ 两者同阶
例2 当x→0时,比较ln(1+x)与x的阶次。
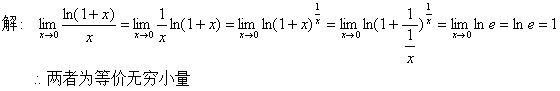
2.3 函数的连续性
一、定义:对于y=f(x)在xo的邻域内有定义,当x取xo+Δx时,y=f(xo+Δx), 则
Δy=f(xo+Δx)-f(xo). if Δx→0, 则Δy→0, 即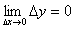 , 则称y=f(x)在xo连续。
, 则称y=f(x)在xo连续。
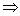 if
if 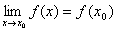 , 则y=f(x)在xo处是连续函数。
, 则y=f(x)在xo处是连续函数。
由定义可得出函数连续的三个必要条件:
(1) y=f(x)在xo有意义
(2)当x→xo时,极限存在
(3)极限等于f(xo)
1、初等函数的连续性
在定义域内一定连续。
2、分段函数的连续性
(1)如果xo不是分段点,则当初等函数看待。
(2)如果xo是分段点,则利用由定义得出的三个必要条件来判断。
例1 求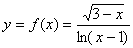 的连续区间。
的连续区间。

例2 已知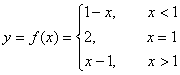 ,讨论y=f(x)在x=1处的连续性。
,讨论y=f(x)在x=1处的连续性。
解:(1)当x=1时,f(1)=2
(2)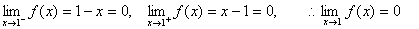

例3 已知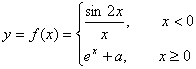 ,求a的值,使f(x)在(-∞,+∞)内连续。
,求a的值,使f(x)在(-∞,+∞)内连续。
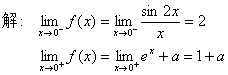
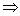 a=1时,f(x)在(-∞,+∞)内连续
a=1时,f(x)在(-∞,+∞)内连续
二、在闭区间连续函数的性质
1、如果y=f(x)在[a, b]连续,则在[a, b]内能取到最大值max和最小值min。
2、零点存在的原理
y=f(x)在[a, b]连续,且f(a)×f(b)<0,则至少存在xo (a, b),使f(xo)=0,xo叫零点。
(a, b),使f(xo)=0,xo叫零点。
例:求证方程x5-5x-1=0在(1, 2)内至少存在一个实数根。
证明:令f(x)= x5-5x-1在[1, 2]连续
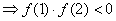
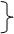 f(1)-5
f(1)-5
f(2)=21
∴ 根据零点存在的原理,至少存在xo (1, 2),使f(xo)=0
(1, 2),使f(xo)=0
∴ 方程在(1, 2)内至少存在一个实数根。
