《经济数学》学习指导
学习开始,要弄清要求,处理好知识广度和深度的关系。一定要把各章基本概念、基本公式和基本运算学好。同时要多花时间在突破重点和难点方面,以求事半功倍,提高效率。
下面逐章明确具体要求,介绍基本内容、重点和难点。
第一章函数,函数内容包括函数定义、函数性质、函数图象、复合函数、初等函数、分段函数等,是学习微积分的预备知识。读者可复习初等数学(高一代数)中关于函数部分的内容,以巩固好基础。
函数重点是函数概念和基本初等函数。要求掌握常量函数、幂函数、指数函数、对数函效、三角函数和反三角函数等六类基本初等函数的定义、定义域、性质和图象,因为由它们经有限四则运算及复合而组成的初等函数是微积分研究的主要对象。复合函数的分解是难点。正确选择中间变量,把复合函数y=f[ψ(x)]分解为简单函数(基本初等函数和多项式)y= f(u),u=ψ(x)的复合,是一种基本训练,务求熟练掌握。
本章经常要求函数的定义域,定义域的求法
(1)分式中分母不能为0
(2)负数不能开偶次方
(3)对数中的真数必须大于0
(4)反三角函数arcsinx, arccosx 中的x必须满足︱x︱≤1
(5)以上解有两个以上的集合,应取交集
第二章 极限与连续
极限与连续内容包括数列极限定义、函数极限的定义、函数的左极限与右极限、无穷小量与无穷大量、极限的运算法则,两个重要极限、函数连续的定义、函数间断点、闭区间连续函数的性质、利用函数连续性计算极限等。重点是函数极限的概念和求极限的方法。难点是未定式极限的计算。
极限的计算方法总结:
(1)应用极限的四则运算法则。这是指函数的四则运算与极限运算交换顺序。函数的和、差、积、商的极限等于极限的和、差、积、商。实际上是把一个复杂函数的极限计算问题转化为分解后各个简单函数的极限计算问题。初学者要注意法则成立的条件、分解后每个简单函效的极限必须存在,分母不能为零。
(2)两个重要极限,第一个重要极限指:

即自变量很小时,s inx的值与近似 x,要注意自变量变化过程为 x→0时,s inx与 x之比的极限为零,两者不要混淆,第二个重要极限有下面三种常见形式:
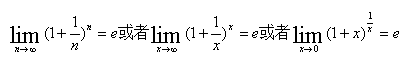
其中e≈2.718为自然对数的底。利用第一个重要极限计算一些三角函数的极限,方法是通过恒等变形凑出一个角的正弦与这个角(趋于零)之比则可知其极限值。利用第二个重要极限解决1 ∞的问题。
(3)利用函数连续性。当f(x)为初等函数(一般可理理解为非分段表示函数)、f(x0)存在,则下式 成立。
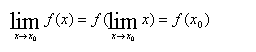
这里 x 0及 f ( x 0 )都必须是确定的有限实数,否则结论不一定成立。例 f(x)=
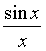 ,
x=0,显然
x→0时,
f(x)→1,而
f(0)是不存在的。
,
x=0,显然
x→0时,
f(x)→1,而
f(0)是不存在的。
(4)自用恒等变换化为连续函数的极限
①含有根式就要进行有理化

因子可考虑分子分母乘其共轭。

例如求 x→∞时,

就要分子分母同乘以

②消去分母为零的因子
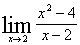
③化商式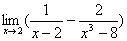
④对x→∞时,有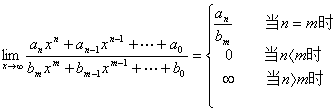
(5)利用无穷小的等价求极限
无穷小最的倒数是无穷大,无穷大的倒数是无穷小。因此经常使用无穷小的等价求极限。常用等价无穷小(x→0),并可以把x理解为表达式
Sinx~x;tanx~x;arctanx~x;arcsinx~x;ln(1+x) ~x;ex-1~x;1-cosx~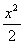
例: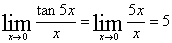
(6) 对于“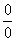 ”或“
”或“ ”、“0·∞”、“∞-∞”、“1∞”、“00”和“∞0”型未定式就要使用洛必达法则求极限。
”、“0·∞”、“∞-∞”、“1∞”、“00”和“∞0”型未定式就要使用洛必达法则求极限。
第三章导数与微分,内容包括导数的定义、导数几何意义、基本初等函数的导数公式、函数四则求导法则,复含函数求导法则。微分定义及计算等。重点是初等函求导数及微分的计算,难点是复合函数求导法则。
1. 导数的定义实质上是求极限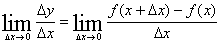 的值,步骤如下
的值,步骤如下
第一步:将x固定,给自变量以增量△x,求出函数的相应的增量值:△y=f(x+△x)-f(x);
第二步:求出△y与△x的比值: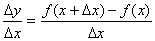
第三步:求极限: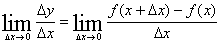 ,如果这一极限存在,其值即为所要求的导数.
,如果这一极限存在,其值即为所要求的导数.
可导一定连续,连续不一定可导.
2. 曲线在点M(x0,y0)的导数y’|x=x0= f’(x0),等于曲线在该点切线的斜率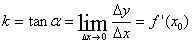 ,根据平面解析几何的知识,已知直线的斜率是k,过点M(x0,y0)的直线方程为y-y0=k(x-x0),而法线的斜率为
,根据平面解析几何的知识,已知直线的斜率是k,过点M(x0,y0)的直线方程为y-y0=k(x-x0),而法线的斜率为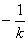 ,法线方程为
,法线方程为 .因此,曲线过切点M(x0,y0)的切线方程是y-y0= f’(x0)(x-x0), 曲线过切点M(x0,y0)的法线方程是
.因此,曲线过切点M(x0,y0)的切线方程是y-y0= f’(x0)(x-x0), 曲线过切点M(x0,y0)的法线方程是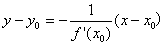 ,这里的y0=f(x0).
,这里的y0=f(x0).
3. P78的22个基本初等函数的导数公式是微积分的核心内容,必须熟练掌握.如果所给求导的初等函数是用代数和、乘积或商复合而成,则利用代数和、乘积或商的导数公式求其导数;如果所给求导的初等函数是采用中间变量复合而成,则将y=f(u)理解为y关于u为变量的基本初等函数,而u= (x)是u关于x为变量的基本初等函数,使用基本初等函数的求导公式分别实施到f(u)和
(x)是u关于x为变量的基本初等函数,使用基本初等函数的求导公式分别实施到f(u)和 (x)上,再利用复合函数的导数公式代入达到求解所有初等函数导数的目的.
(x)上,再利用复合函数的导数公式代入达到求解所有初等函数导数的目的.
4. 对于隐函数的导数,我们只需对等式两边求导,得到含有y’的一个方程,再将它看成是一个未知变量,将其求解出来,得到一个y’关于x和y两个变量的表达式,这个表达式就是隐函数的导数.取对数求导法,就先对所给的函数式y=f(x)的两边取对数,再用隐函数的求导法则求出y’,再求出y’的表达式,求出右边的表达式的y要用相应的函数式f(x)代替.
取对数求导法主要用于(1)多个函数连乘除的情形,简化其计算;(2)幂指函数的情形.
5. 进行一次求导后,f’(x)还是关于 x的函数,可以再进行一次或以上求导,便是高阶导数的概念,二阶导数就是求二次导数,如此类推.
6. 可微分的充分必要条件是函数可导,要求函数y=f(x)微分dy,只要先求函数的导数y’=f’(x),再乘以自变量的微分f’(x)dx即为所求.
本章是微积分学基本的内容,不仅要会,而且务求熟练掌握。同学们必须牢记基本求导表的全部14条公式,且会灵活套用。应用四则运算求导法则的时候要注意函数的代数和求导允许逐项求,但函数的乘积或函数的商求导,不允许逐项求,应用复合函数求导法则,记住复合函数y=f[Ψ(x)]对自变量u的导数,等于因变量y对中间变量u的导数f’(u)乘以中间变量u对自变x的导数Ψ’(x).即yx’=yu’ux’=f’(u)·Ψ’(x),初学者往往会漏掉中间变量对自变量的导数,应记住求导没有形式一不变性,即因变量对中间变量的导数一般不等于因变量对自变量的导数。
第四章中值定理与导数的应用,内容包括微分中值定理、罗彼塔法则、函数的增减性判别法、函数的极值及其求法、曲线凹向及其判别法、拐点及其求法、最大值和最小值应用问题。重点是拉格朗日微分中值定理、罗彼塔法则和最值应用问题。难点是经济优化问题。
1. 使用洛必塔L’Hospital法则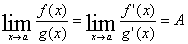 (或∞)求
(或∞)求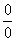 、
、 未定型的极限,如果
未定型的极限,如果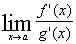 还是
还是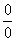 或
或 型的未定式,则可以继续使用洛比达法则,即
型的未定式,则可以继续使用洛比达法则,即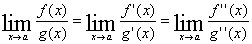 ,如此类推,直到求出极限为止.
,如此类推,直到求出极限为止.
2. 对于“∞-∞”、“0·∞”、“1∞”、“00”和“∞0”型等未定式,采用下列方法求解.
(1)对于“∞-∞”的未定式,先利用通分,将其化为“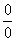 ”型或“
”型或“ ”型再应用洛必塔L’Hospital法则求解.
”型再应用洛必塔L’Hospital法则求解.
(2)对于“0·∞”的未定式,将其乘积的形式化为除的形式,转变方式为:在某一变化过程中,若f(x)→0,g(x)→∞,则f(x) g(x)=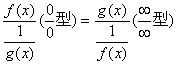 变为“
变为“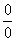 ”型或“
”型或“ ”型,再应用洛必塔L’Hospital法则求解.
”型,再应用洛必塔L’Hospital法则求解.
(3)对于“1∞”、“00”和“∞0”型等未定式,先将其化为e为底的指数函数的极限,其指数成为“0·∞”的未定式的极限,利用指数函数的连续性,可以直接在指数上取极限,使用方法(2),求得指数的极限后再利用对数的性质还原.
3.使用函数y’=f’(x)的符号判断函数的增减性.若f’(x)≥0,则函数y=f(x)在(a,b)内单调增加(或称为递增),若f’(x)≤0,则函数y=f(x)在(a,b)内单调减少(或称为递减).
4. 函数f’(x)=0的点称为驻点, 如果驻点x0的左邻域,f’(x)>0, 在点x0的右邻域,f’(x)<0,(或者f”(x0)<0)则函数f(x)在点x0取得极大值f(x0).如果在点x0的左邻域,f’(x)<0, 在点x0的右邻域,f’(x)>0,(或者f”(x0)>0)则函数f(x)在点x0取得极小值f(x0).如果f’(x) 在点x0邻域内不改变符号,则函数f(x)在点x0不取得极值.
5. 使用函数f”(x)符号来判断函数的凹凸区间和求拐点,如果在区间(a,b)内f”(x)>0,则曲线y=f(x)在区间(a,b)内是上凹的(简称为凹);如果在区间(a,b)内f”(x)<0,则曲线y=f(x)在区间(a,b)内是下凹的(简称为凸).若f”(x) 在x0的左右邻域改变符号,则x0是拐点.
罗彼塔法则是计算函数极限的重要工具,过去需要三角公式、代数公式进行恒等变形后才能定值的“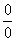 ”或“
”或“ ”型未定式,采用罗彼塔法则后一般会变得简单多了,而许多过去没有办法计算的未定式,借助这个法则才能计算出来,罗彼塔法则指出两个无穷小(或两个无穷大)之比的极限等于它们导数之比的极限。使用时注意对自变量的变化过程,趋于定点或趋于无穷)是没有限制的,只要在指定的自变量过程中,极限是“
”型未定式,采用罗彼塔法则后一般会变得简单多了,而许多过去没有办法计算的未定式,借助这个法则才能计算出来,罗彼塔法则指出两个无穷小(或两个无穷大)之比的极限等于它们导数之比的极限。使用时注意对自变量的变化过程,趋于定点或趋于无穷)是没有限制的,只要在指定的自变量过程中,极限是“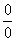 ”或“
”或“ ”型未定式,使用一次后的极限仍是一个“
”型未定式,使用一次后的极限仍是一个“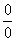 ”或“
”或“ ”未定型,可以连续使用。罗彼塔法则采用了导数这个工具计算极限,初学者不要误解函数商的极限等于商的导数的极限,而应是分子导致与分母导数之商的极限,凡运用罗彼塔法则的未定式是不能直接应用极限的四则运算法则进行计算的,因为这时肯定有些极限不存在或分母极限为零。对于“0˙∞”、“∞-∞”未定式,可以通过通分、取对数等方式进行恒等变形后化作“
”未定型,可以连续使用。罗彼塔法则采用了导数这个工具计算极限,初学者不要误解函数商的极限等于商的导数的极限,而应是分子导致与分母导数之商的极限,凡运用罗彼塔法则的未定式是不能直接应用极限的四则运算法则进行计算的,因为这时肯定有些极限不存在或分母极限为零。对于“0˙∞”、“∞-∞”未定式,可以通过通分、取对数等方式进行恒等变形后化作“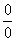 ”或“
”或“ ”这两种基本类型未定式,然后使用罗彼塔法则。“
”这两种基本类型未定式,然后使用罗彼塔法则。“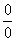 ”或“
”或“ ”型时注意选择,避免法则失效。
”型时注意选择,避免法则失效。
曲线的几何形态与函数的图形密切相连,有关单调性和凹凸性判别定理应借助几何意义记牢。函数的一阶导数的正负号决定了函数的单调性,驻点(一阶导数为0点)可能改变函数的单调性,极值点一定改变函数的单调性;函数的二阶导数的正负号决定了函数的凹凸性,二阶导数为0的点可能改变函效的凹性,拐点一定改变函数凹凸性。曲线的单调性与凹凸性无必然联系)单调增加的曲线既可能是凹的也可能是凸的。有关定理不要互相混淆。
对可导函数而言,可能的最大值(最小值)点是函数的驻点、区间端点、比较它们的函数值,最大者为函数的最大值,最小值为函数的最小值。特别地,函数只有一个极值点,则要应用极值判别法判定它是极大值点还是极小值点,若是极大值点也必是最大值点,若是极小值点也必是最小值点。在经济问题中为了发挥最大的经济效益,常常会遇到如何使用料最省、利润最大、成本最小筹问题,对这类问题,关键是正确写出目标函数,问题就转化为求它的最值点和最值了。为此,对总成本函数、总收益函数、总利润函数、边际成本、平均成本等等概念和互相转换是应该掌握好的。
第五章不定积分,内容包括原函数与不定积分的定义、不定积分的性质、基本积分公式、换元积分法、分部积分法。重点是基本积分公式、换元积分法及分部积分法,难点是换元积分法中变量替换函数的选择。
换元积分法是对应于复合函数求导法则的积分方法。换元就是更换积分变量、使之对新变元能应用基本积分公式。根据选择新变元的方式不同换元法为第一换元法与第二换元法,使用第一换元法,被积函数呈某复合函数导数形式y=f[Ψ(x)] Ψ’(x),其中第一部分仍y=f[Ψ(x)]是复合函效,第二部分恰为复合函数y=f[Ψ(x)]的中间变量u=Ψ(x)的导致,选择u=Ψ(x)为新变元,则f(x)=f[Ψ(x)]换作f(u),Ψ(x)dx就凑成了du,就变为f(u)的积分了,这里关键是凑出新变量u的凑分,所以第一换元法也叫凑微分法。常见的凑微分有:
① dx=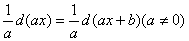
② adx= dax=d(ax+b)
③ xdx=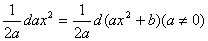
④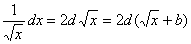
⑤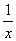 dx=dlnx=d(lnx+b)
dx=dlnx=d(lnx+b)
⑥ex=dex= d(aex+b)
d(aex+b)
⑦ cosxdx=d(sinx+b) dtanx=sec2xdx
⑧ sinxdx=-d(cosx+b)
⑨ 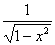 dx = darcsinx (-1<x<1)
dx = darcsinx (-1<x<1)
⑩ 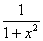 dx = darctanx (-1<x<1)
dx = darctanx (-1<x<1)
第二换元法多用于被积函数含自变量的无理根式,最常见的是含
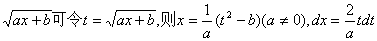
代入原积分,即变为对新变元t的积分了。
一般情况,当被积函数含有:
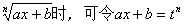

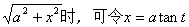

分部积分法是对应于乘积求导法则的积分方法,据乘积求导公式(uv)’=u’v+uv’,两边积分有uv’dx=uv-vu’dx或udv=uv-vdu,这两条分部公式常见于幂函数与另一种函数的乘积。当另一函数为三角函数或指数(或指数函数)为u’;当另一函数为对数函数或反三角函数时,选法相反,应选幂函数为v’,对数函数(或反三角函数)为u,使用分部公式的关键是选好u和v。原则是v易求。v’,vu’易积分。公式中出现了u、u’、u、v’,四个不同函数,注意不要混淆。常用的分部积分式子有:
∫xaekxdx
∫xalnbxdx
∫xasinbxdx 或 ∫xacosbxdx
∫xaarcsinbxdx 或 ∫xaarccosbxdx
∫xaarctanbxdx 或 ∫xaarccotbxdx
∫lnbxdx
∫arctanbxdx
第六章定积分。内容包括定积分定义、定积分性质、牛顿—莱布尼兹公式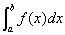 =F(b)-F(a)、定积分换元积分法、定积分分部积分法、广义积分。重点是牛吨—莱布尼兹公式、难点是定积分的求法。定积分与不定积分概念不同,不定积分是函数的集合,而定积分计算出来是一个数。不过两者关系密切,表现在牛顿—莱布尼兹公式中,这条公式把大多数定积分计算问题转化为不定积的计算,指出一个函数在区间上的定积分,等于它任一原函数在区间端点函数值的差。学习中注意定积分换元法与不定积分换元法的异同。在选择新变元的方法上,两者是完全一样的,不同的是积分的换元必须换限,换限也就不必要“还原”(把新变量换回老变量),从而简化了计算。分部积分两者u,v’的选择也完全一样,定积分的分部积分就要把限处理好。
=F(b)-F(a)、定积分换元积分法、定积分分部积分法、广义积分。重点是牛吨—莱布尼兹公式、难点是定积分的求法。定积分与不定积分概念不同,不定积分是函数的集合,而定积分计算出来是一个数。不过两者关系密切,表现在牛顿—莱布尼兹公式中,这条公式把大多数定积分计算问题转化为不定积的计算,指出一个函数在区间上的定积分,等于它任一原函数在区间端点函数值的差。学习中注意定积分换元法与不定积分换元法的异同。在选择新变元的方法上,两者是完全一样的,不同的是积分的换元必须换限,换限也就不必要“还原”(把新变量换回老变量),从而简化了计算。分部积分两者u,v’的选择也完全一样,定积分的分部积分就要把限处理好。
定积分的应用。平面图形面积、定积分在经济方面的应用等在统计分析中,常常用到平面目形的面积计算问题。若平面图形是由边界函数绘出,首先就必须正确无误地画出边界,求出交点标明图上,并把这些边界曲线共同围成的封闭图形打上阴影标明。然后利用非负函数在某区间上定积分等于相应的曲边梯形面积的原理,把面积问题转化为定积分计算问题。对较复杂的图形,应适当加辅助线,使所求图形面积为一些曲边梯形面积之和或差。定积分的另一个应用,是解决一些诸如边际成本、边际收益求总成本、总收益等经济问题,也就是积分问题,用定积分或不定积分来解决。用定积分则积分限是变数(变上限函数),用不定积分比较易理解,不过计算出来的积分常数还要利用给定附加条件加以确定。难点是定积分的应用。
介于曲线y=f(x)[f(x)≥0]和直线x=a,x=b(a<b)以及x轴之间的曲边梯形的面积S为
S=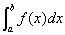 .
.
旋转体的体积为V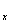 =
= πf 2(x)dx.
πf 2(x)dx.
