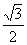高考递推数列题型分类归纳解析
各种数列问题在很多情形下,就是对数列通项公式的求解。特别是在一些综合性比较强的数列问题中,数列通项公式的求解问题往往是解决数列难题的瓶颈。本文总结出几种求解数列通项公式的方法,希望能对大家有帮助。
类型1 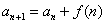
解法:把原递推公式转化为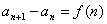 ,利用累加法(逐差相加法)求解。
,利用累加法(逐差相加法)求解。
例:已知数列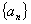 满足
满足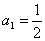 ,
,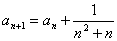 ,求
,求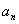 。
。
解:由条件知: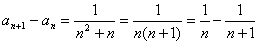
分别令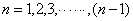 ,代入上式得
,代入上式得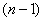 个等式累加之,即
个等式累加之,即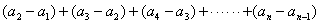
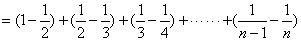
所以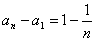
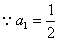 ,
,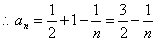
变式:(2004,全国I,个理22.本小题满分14分)
已知数列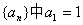 ,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k, 其中k=1,2,3,…….
,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k, 其中k=1,2,3,…….
(I)求a3, a5;
(II)求{ an}的通项公式.
解:
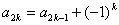 ,
,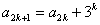

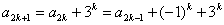 ,即
,即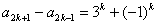

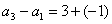 ,
,
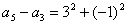
…… ……
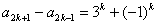
将以上k个式子相加,得
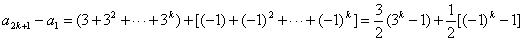
将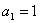 代入,得
代入,得
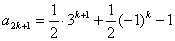 ,
,
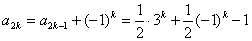 。
。
经检验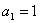 也适合,
也适合,
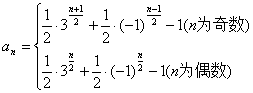
类型2 
解法:把原递推公式转化为 ,利用累乘法(逐商相乘法)求解。
,利用累乘法(逐商相乘法)求解。
例:已知数列 满足
满足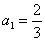 ,
,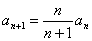 ,求
,求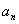 。
。
解:由条件知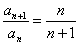 ,分别令
,分别令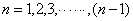 ,代入上式得
,代入上式得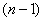 个等式累乘之,即
个等式累乘之,即
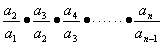
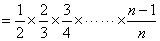
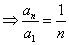
又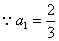 ,
,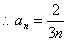
例:已知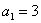 ,
,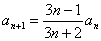
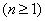 ,求
,求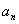 。
。
解: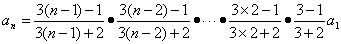
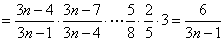 。
。
变式:(2004,全国I,理15.)已知数列{an},满足a1=1,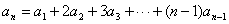 (n≥2),则{an}的通项
(n≥2),则{an}的通项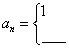
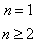
解:由已知,得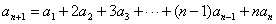 ,用此式减去已知式,得
,用此式减去已知式,得
当 时,
时,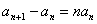 ,即
,即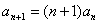 ,又
,又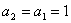 ,
,
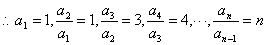 ,将以上n个式子相乘,得
,将以上n个式子相乘,得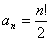
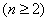
类型3  (其中p,q均为常数,
(其中p,q均为常数,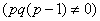 )。
)。
解法(待定系数法):把原递推公式转化为: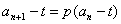 ,其中
,其中 ,再利用换元法转化为等比数列求解。
,再利用换元法转化为等比数列求解。
例:已知数列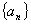 中,
中,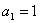 ,
,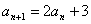 ,求
,求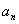 .
.
解:设递推公式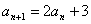 可以转化为
可以转化为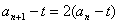 即
即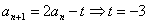 .故递推公式为
.故递推公式为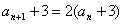 ,令
,令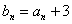 ,则
,则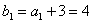 ,且
,且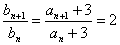 .所以
.所以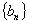 是以
是以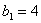 为首项,2为公比的等比数列,则
为首项,2为公比的等比数列,则 ,所以
,所以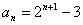 .
.
变式:(2006,重庆,文,14)
在数列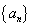 中,若
中,若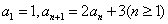 ,则该数列的通项
,则该数列的通项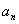
 _______________
_______________
(key: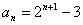 )
)
变式:(2006. 福建.理22.本小题满分14分)
已知数列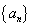 满足
满足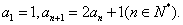
(I)求数列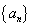 的通项公式;
的通项公式;
(II)若数列{bn}滿足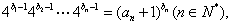 证明:数列{bn}是等差数列;
证明:数列{bn}是等差数列;
(Ⅲ)证明: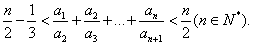
(I)解: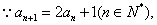
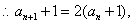
 是以
是以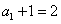 为首项,2为公比的等比数列
为首项,2为公比的等比数列
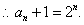
即 
(II)证法一: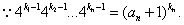
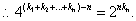
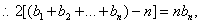 ①
①
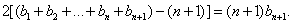 ②
②
②-①,得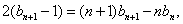
即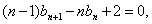
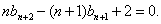
③-④,得 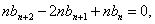
即 
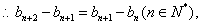
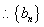 是等差数列
是等差数列
证法二:同证法一,得
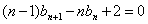
令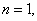 得
得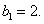
设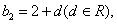 下面用数学归纳法证明
下面用数学归纳法证明 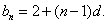
(1)当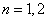 时,等式成立
时,等式成立
(2)假设当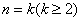 时,
时,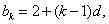 那么
那么
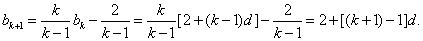
这就是说,当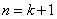 时,等式也成立
时,等式也成立
根据(1)和(2),可知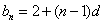 对任何
对任何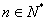 都成立
都成立
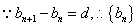 是等差数列
是等差数列
(III)证明:
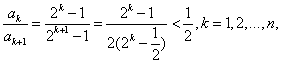
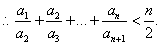
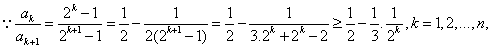
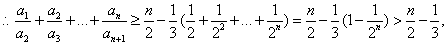
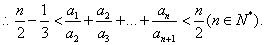
变式:递推式: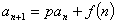 。解法:只需构造数列
。解法:只需构造数列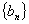 ,消去
,消去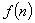 带来的差异.
带来的差异.
类型4  (其中p,q均为常数,
(其中p,q均为常数,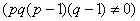 )。 (或
)。 (或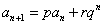 ,其中p,q, r均为常数) 。
,其中p,q, r均为常数) 。
解法:一般地,要先在原递推公式两边同除以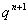 ,得:
,得: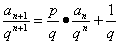 引入辅助数列
引入辅助数列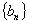 (其中
(其中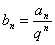 ),得:
),得: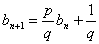 再待定系数法解决。
再待定系数法解决。
例:已知数列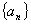 中,
中,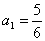 ,
,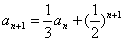 ,求
,求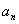 。
。
解:在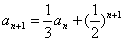 两边乘以
两边乘以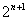 得:
得: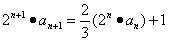
令 ,则
,则 ,解之得:
,解之得: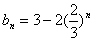
所以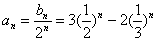
变式:(2006,全国I,理22,本小题满分12分)
设数列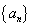 的前
的前 项的和
项的和 ,
,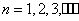
(Ⅰ)求首项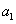 与通项
与通项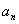 ;(Ⅱ)设
;(Ⅱ)设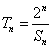 ,
,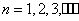 ,证明:
,证明:
解:(I)当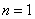 时,
时,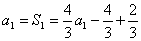
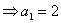 ;
;
当 时,
时,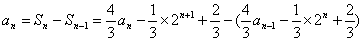 ,即
,即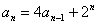 ,利用
,利用 (其中p,q均为常数,
(其中p,q均为常数,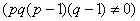 )。 (或
)。 (或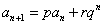 ,其中p,q, r均为常数)的方法,解之得:
,其中p,q, r均为常数)的方法,解之得: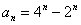
(Ⅱ)将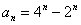 代入①得 Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
代入①得 Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以, 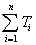 =
= 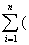 - ) = ×( - ) <
- ) = ×( - ) <
类型5 递推公式为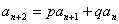 (其中p,q均为常数)。
(其中p,q均为常数)。
解法一(待定系数法):先把原递推公式转化为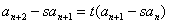
其中s,t满足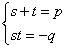
解法二(特征根法):对于由递推公式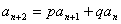 ,
,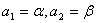 给出的数列
给出的数列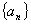 ,方程
,方程 ,叫做数列
,叫做数列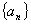 的特征方程。若
的特征方程。若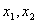 是特征方程的两个根,当
是特征方程的两个根,当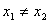 时,数列
时,数列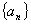 的通项为
的通项为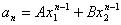 ,其中A,B由
,其中A,B由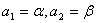 决定(即把
决定(即把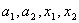 和
和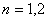 ,代入
,代入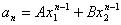 ,得到关于A、B的方程组);当
,得到关于A、B的方程组);当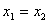 时,数列
时,数列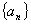 的通项为
的通项为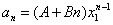 ,其中A,B由
,其中A,B由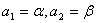 决定(即把
决定(即把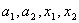 和
和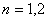 ,代入
,代入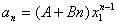 ,得到关于A、B的方程组)。
,得到关于A、B的方程组)。
解法一(待定系数——迭加法):
数列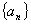 :
: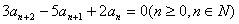 ,
, 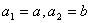 ,求数列
,求数列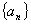 的通项公式。
的通项公式。
由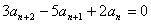 ,得
,得
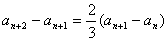 ,
,
且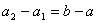 。
。
则数列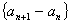 是以
是以 为首项,
为首项,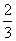 为公比的等比数列,于是
为公比的等比数列,于是
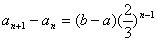 。把
。把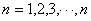 代入,得
代入,得
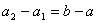 ,
,
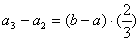 ,
,
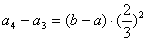 ,
,

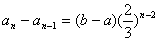 。
。
把以上各式相加,得
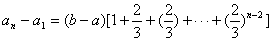
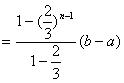 。
。
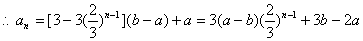 。
。
解法二(特征根法):数列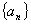 :
: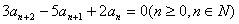 ,
, 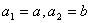 的特征方程是:
的特征方程是: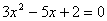 。
。
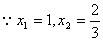 ,
,

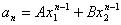
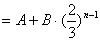 。
。
又由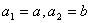 ,于是
,于是
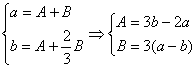
故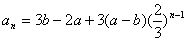
例:已知数列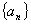 中,
中,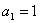 ,
,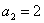 ,
,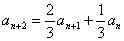 ,求
,求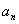 。
。
解:由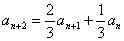 可转化为
可转化为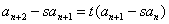
即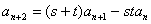
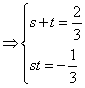
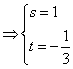 或
或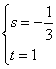
这里不妨选用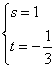 (当然也可选用
(当然也可选用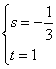 ,大家可以试一试),则
,大家可以试一试),则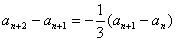
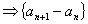 是以首项为
是以首项为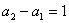 ,公比为
,公比为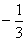 的等比数列,所以
的等比数列,所以 ,应用类型1的方法,分别令
,应用类型1的方法,分别令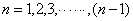 ,代入上式得
,代入上式得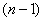 个等式累加之,即
个等式累加之,即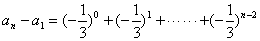
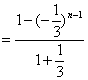
又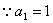 ,所以
,所以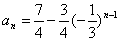 。
。
变式:(2006,福建,文,22,本小题满分14分)
已知数列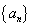 满足
满足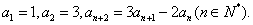
(I)证明:数列 是等比数列;
是等比数列;
(II)求数列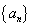 的通项公式;
的通项公式;
(III)若数列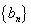 满足
满足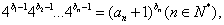 证明
证明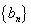 是等差数列
是等差数列
(I)证明: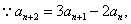

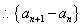 是以
是以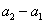
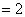 为首项,2为公比的等比数列
为首项,2为公比的等比数列
(II)解:由(I)得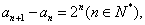
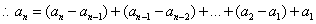
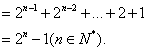
(III)证明: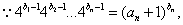

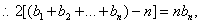 ①
①
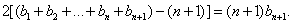 ②
②
②-①,得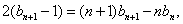
即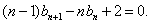 ③
③
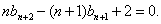 ④
④
④-③,得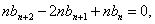
即
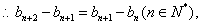
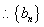 是等差数列
是等差数列
类型6 递推公式为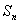 与
与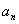 的关系式。(或
的关系式。(或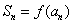 )
)
解法:这种类型一般利用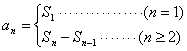 与
与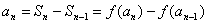 消去
消去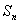
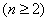 或与
或与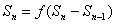
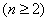 消去
消去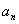 进行求解。
进行求解。
例:已知数列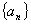 前n项和
前n项和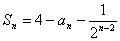 .
.
(1)求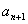 与
与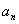 的关系;(2)求通项公式
的关系;(2)求通项公式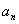 .
.
解:(1)由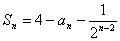 得:
得:
于是
所以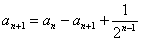
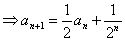 .
.
(2)应用类型4( (其中p,q均为常数,
(其中p,q均为常数,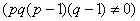 ))的方法,上式两边同乘以
))的方法,上式两边同乘以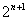 得:
得: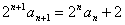
由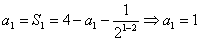 .于是数列
.于是数列 是以2为首项,2为公差的等差数列,所以
是以2为首项,2为公差的等差数列,所以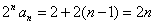
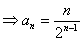
变式:(2006,陕西,理,20 本小题满分12分)
本小题满分12分)
已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an
解: ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1=3
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2)
当a1=3时,a3=13,a15=73 a1, a3,a15不成等比数列∴a1≠3;
a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3
变式: (2005,江西,文,22.本小题满分14分)
已知数列{an}的前n项和Sn满足Sn-Sn-2=3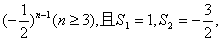 求数列{an}的通项公式.
求数列{an}的通项公式.
解:
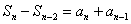 ,
,

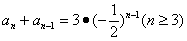 ,两边同乘以
,两边同乘以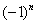 ,可得
,可得
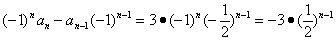
令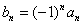

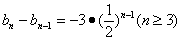
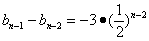
…… ……
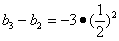

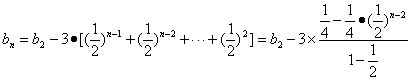
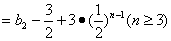
又
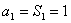 ,
,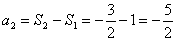 ,
,

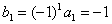 ,
,

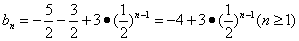 。
。

类型7 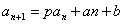
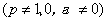
解法:这种类型一般利用待定系数法构造等比数列,即令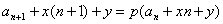 ,与已知递推式比较,解出
,与已知递推式比较,解出 ,从而转化为
,从而转化为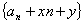 是公比为
是公比为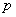 的等比数列。
的等比数列。
例:设数列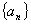 :
: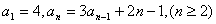 ,求
,求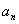 .
.
解:设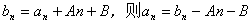 ,将
,将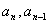 代入递推式,得
代入递推式,得
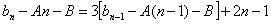
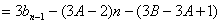
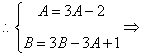
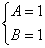
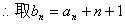 …(1)则
…(1)则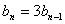 ,又
,又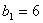 ,故
,故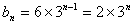 代入(1)得
代入(1)得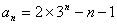
说明:(1)若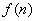 为
为 的二次式,则可设
的二次式,则可设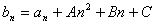 ;(2)本题也可由
;(2)本题也可由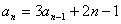 ,
,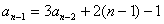 (
(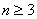 )两式相减得
)两式相减得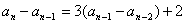 转化为
转化为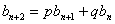 求之.
求之.
变式:(2006,山东,文,22,本小题满分14分)
已知数列{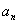 }中,
}中,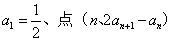 在直线y=x上,其中n=1,2,3…
在直线y=x上,其中n=1,2,3…
(Ⅰ)令
(Ⅱ)求数列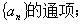
(Ⅲ)设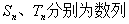
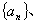
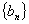 的前n项和,是否存在实数
的前n项和,是否存在实数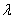 ,使得数列
,使得数列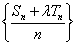 为等差数列?若存在,试求出
为等差数列?若存在,试求出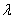
 若不存在,则说明理由
若不存在,则说明理由
解:(I)由已知得 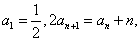
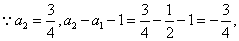
又
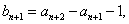
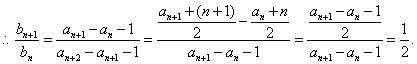
 是以
是以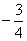 为首项,以
为首项,以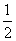 为公比的等比数列
为公比的等比数列
(II)由(I)知,
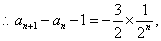

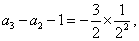

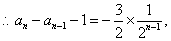
将以上各式相加得:
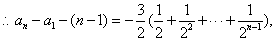
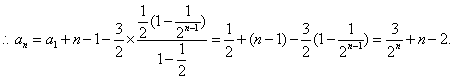
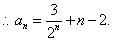
(III)解法一:
存在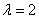 ,使数列
,使数列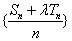 是等差数列
是等差数列
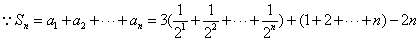
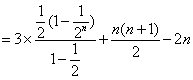
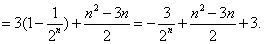
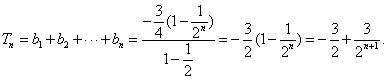
数列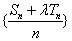 是等差数列的充要条件是
是等差数列的充要条件是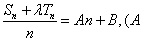 、
、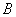 是常数
是常数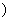
即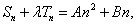
又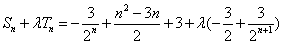
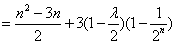
 当且仅当
当且仅当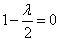 ,即
,即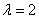 时,数列
时,数列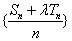 为等差数列
为等差数列
解法二:
存在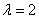 ,使数列
,使数列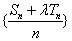 是等差数列
是等差数列
由(I)、(II)知,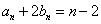

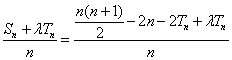
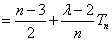
又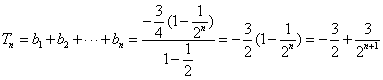
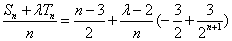
 当且仅当
当且仅当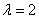 时,数列
时,数列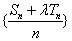 是等差数列
是等差数列
类型8 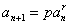

解法:这种类型一般是等式两边取对数后转化为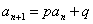 ,再利用待定系数法求解。
,再利用待定系数法求解。
例:已知数列{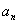 }中,
}中,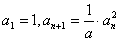
 ,求数列
,求数列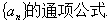
解:由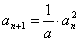 两边取对数得
两边取对数得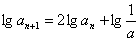 ,
,
令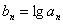 ,则
,则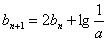 ,再利用待定系数法解得:
,再利用待定系数法解得: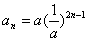 。
。
变式:(2005,江西,理,21.本小题满分12分)
已知数列
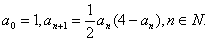
(1)证明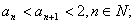
(2)求数列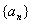 的通项公式an.
的通项公式an.
解:用数学归纳法并结合函数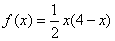 的单调性证明:
的单调性证明:
(1)方法一 用数学归纳法证明:
1°当n=1时,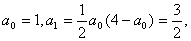
∴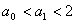 ,命题正确.
,命题正确.
2°假设n=k时有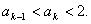
则
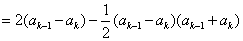
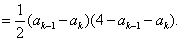
而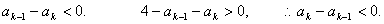
又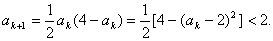
∴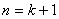 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有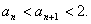
方法二:用数学归纳法证明:
1°当n=1时,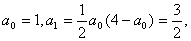 ∴
∴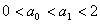 ;
;
2°假设n=k时有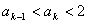 成立,
成立,
令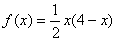 ,
,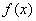 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: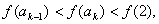 即
即
也即当n=k+1时 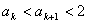 成立,所以对一切
成立,所以对一切
(2)解法一: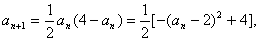
所以 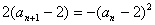
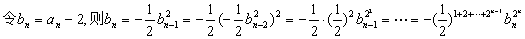 ,
,
又bn=-1,所以
解法二:


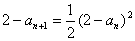
由(I)知, ,两边取以2为底的对数,
,两边取以2为底的对数,

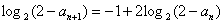
令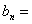
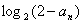 ,则
,则
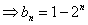

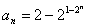 或
或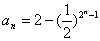
变式:(2006,山东,理,22,本小题满分14分)
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
记bn=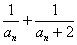 ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+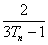 =1
=1
解:(Ⅰ)由已知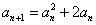 ,
,

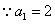
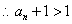 ,两边取对数得
,两边取对数得
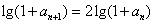 ,
,
即
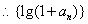 是公比为2的等比数列
是公比为2的等比数列
(Ⅱ)由(Ⅰ)知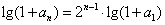
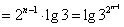
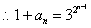 (*)
(*)
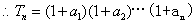
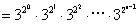
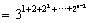 =
=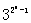
由(*)式得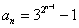
(Ⅲ)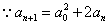 ,
, 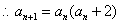 ,
,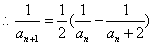
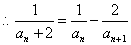 ,又
,又 ,
,
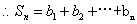
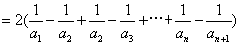

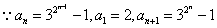
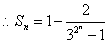 ,又
,又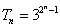 ,
,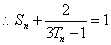

类型9 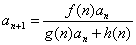
解法:这种类型一般是等式两边取倒数后换元转化为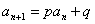 。
。
例:已知数列{an}满足: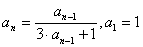 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
解:取倒数: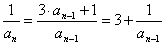
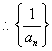 是等差数列,
是等差数列,
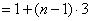

变式:(2006,江西,理,22,本大题满分14分)
已知数列{an}满足:a1= ,且an=
,且an=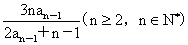
(1) 求数列{an}的通项公式;
(2) 证明:对于一切正整数n,不等式a1·a2·……an<2·n!
解:(1)将条件变为:1-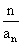 =
=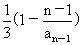 ,因此{1-
,因此{1-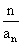 }为一个等比数列,其首项为
}为一个等比数列,其首项为
1-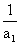 =
=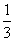 ,公比
,公比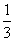 ,从而1-
,从而1-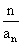 =
=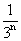 ,据此得an=
,据此得an=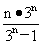 (n³1)…………1°
(n³1)…………1°
(2)证:据1°得,a1·a2·…an=
为证a1·a2·……an<2·n!
只要证nÎN*时有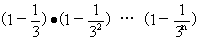 >
>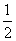 …………2°
…………2°
显然,左端每个因式都是正数,先证明,对每个nÎN*,有
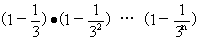 ³1-(
³1-(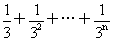 )…………3°
)…………3°
用数学归纳法证明3°式:
(i) n=1时,3°式显然成立,
(ii) 设n=k时,3°式成立,
即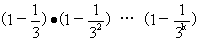 ³1-(
³1-(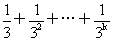 )
)
则当n=k+1时,
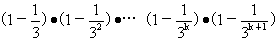 ³〔1-(
³〔1-(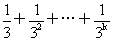 )〕·(
)〕·(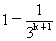 )
)
=1-(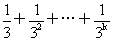 )-
)-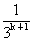 +
+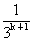 (
(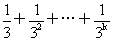 )
)
³1-(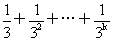 +
+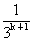 )即当n=k+1时,3°式也成立
)即当n=k+1时,3°式也成立
故对一切nÎN*,3°式都成立
利用3°得,
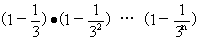 ³1-(
³1-(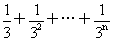 )=1-
)=1-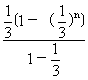
=1-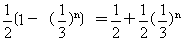 >
>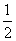
故2°式成立,从而结论成立
类型10 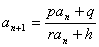
解法:如果数列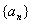 满足下列条件:已知
满足下列条件:已知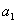 的值且对于
的值且对于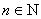 ,都有
,都有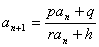 (其中p、q、r、h均为常数,且
(其中p、q、r、h均为常数,且 ),那么,可作特征方程
),那么,可作特征方程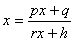 ,当特征方程有且仅有一根
,当特征方程有且仅有一根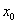 时,则
时,则 是等差数列;当特征方程有两个相异的根
是等差数列;当特征方程有两个相异的根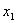 、
、 时,则
时,则 是等比数列。
是等比数列。
例:已知数列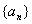 满足性质:对于
满足性质:对于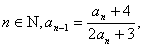 且
且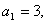 求
求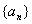 的通项公式.
的通项公式.
解: 数列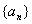 的特征方程为
的特征方程为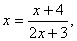 变形得
变形得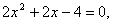 其根为
其根为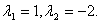 故特征方程有两个相异的根,使用定理2的第(2)部分,则有
故特征方程有两个相异的根,使用定理2的第(2)部分,则有
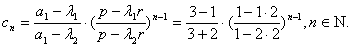
∴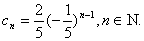
∴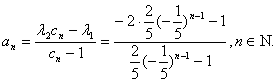
即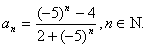
例:已知数列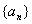 满足:对于
满足:对于 都有
都有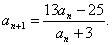
(1)若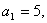 求
求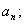 (2)若
(2)若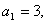 求
求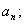 (3)若
(3)若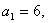 求
求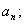
(4)当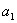 取哪些值时,无穷数列
取哪些值时,无穷数列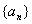 不存在?
不存在?
解:作特征方程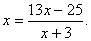 变形得
变形得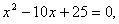
特征方程有两个相同的特征根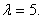 依定理2的第(1)部分解答.
依定理2的第(1)部分解答.
(1)∵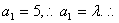 对于
对于 都有
都有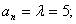
(2)∵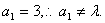
∴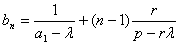
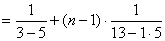
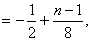
令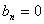 ,得
,得 .故数列
.故数列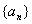 从第5项开始都不存在,
从第5项开始都不存在,
当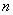 ≤4,
≤4,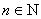 时,
时,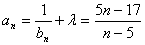 .
.
(3)∵ ∴
∴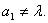
∴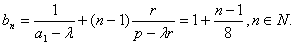
令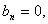 则
则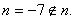 ∴对于
∴对于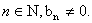
∴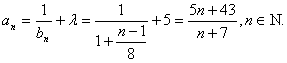
(4)、显然当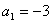 时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知,
时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知,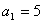 时,数列
时,数列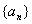 是存在的,当
是存在的,当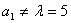 时,则有
时,则有 令
令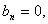 则得
则得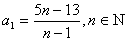 且
且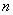 ≥2.
≥2.
∴当 (其中
(其中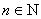 且N≥2)时,数列
且N≥2)时,数列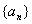 从第
从第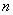 项开始便不存在.
项开始便不存在.
于是知:当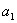 在集合
在集合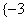 或
或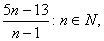 且
且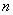 ≥2}上取值时,无穷数列
≥2}上取值时,无穷数列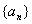 都不存在.
都不存在.
变式:(2005,重庆,文,22,本小题满分12分)
数列 记
记
(Ⅰ)求b1、b2、b3、b4的值;
(Ⅱ)求数列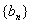 的通项公式及数列
的通项公式及数列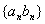 的前n项和
的前n项和
解法一:由已知,得 ,其特征方程为
,其特征方程为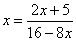 解之得,
解之得,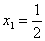 或
或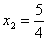

 ,
,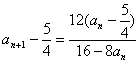

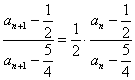 ,
, 
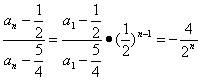

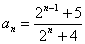
解法二:
(I)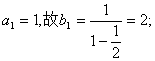
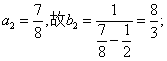
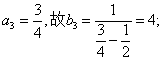
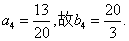
(II)因 ,
,
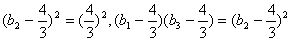
故猜想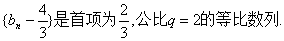
因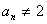 ,(否则将
,(否则将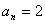 代入递推公式会导致矛盾)
代入递推公式会导致矛盾)
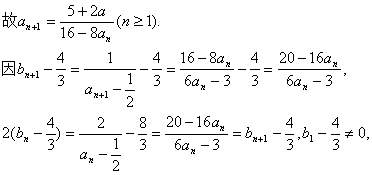
故 的等比数列.
的等比数列.
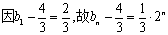 ,
, 
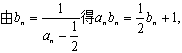

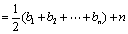
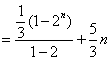
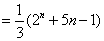
解法三:
(Ⅰ)由
整理得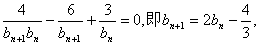
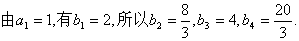
(Ⅱ)由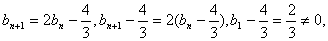
所以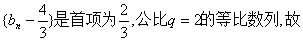

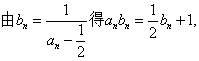
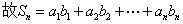
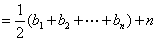
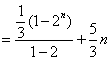

解法四:
(Ⅰ)同解法一
(Ⅱ)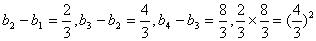
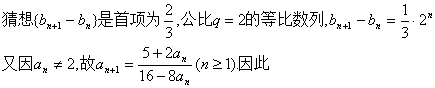
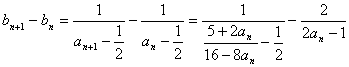

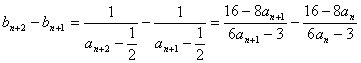

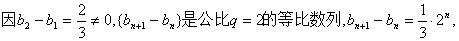
从而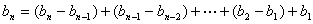
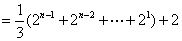
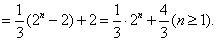
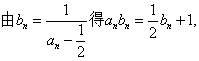
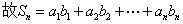
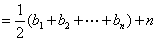
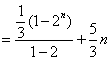

类型11 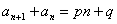 或
或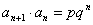
解法:这种类型一般可转化为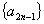 与
与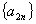 是等差或等比数列求解。
是等差或等比数列求解。
例:(I)在数列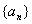 中,
中,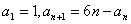 ,求
,求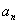
(II)在数列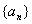 中,
中, ,求
,求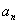
类型12 归纳猜想法
解法:数学归纳法
变式:(2006,全国II,理,22,本小题满分12分)
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,…
(Ⅰ)求a1,a2;
(Ⅱ){an}的通项公式
提示:1 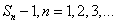 为方程的根,代入方程可得
为方程的根,代入方程可得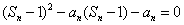
将n=1和n=2代入上式可得
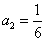
2 求出
求出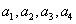 等,可猜想
等,可猜想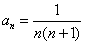 并用数学归纳法进行证明,本题主要考察 一般数列的通项公式与求和公式间的关系
并用数学归纳法进行证明,本题主要考察 一般数列的通项公式与求和公式间的关系
3 方程的根的意义(根代入方程成立)
方程的根的意义(根代入方程成立)
4 数学归纳法证明数列的通项公式(也可以把
数学归纳法证明数列的通项公式(也可以把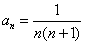 分开为
分开为 ,可得
,可得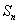
解:(Ⅰ)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,
于是(a1-1)2-a1(a1-1)-a1=0,解得a1=
当n=2时,x2-a2x-a2=0有一根为S2-1=a2-,
于是(a2-)2-a2(a2-)-a2=0,解得a1=
(Ⅱ)由题设(Sn-1)2-an(Sn-1)-an=0,
即 Sn2-2Sn+1-anSn=0
当n≥2时,an=Sn-Sn-1,代入上式得
Sn-1Sn-2Sn+1=0 ①
由(Ⅰ)知S1=a1=,S2=a1+a2=+=
由①可得S3=
由此猜想Sn=,n=1,2,3,… ……8分
……8分
下面用数学归纳法证明这个结论
(i)n=1时已知结论成立
(ii)假设n=k时结论成立,即Sk=,
当n=k+1时,由①得Sk+1=,即Sk+1=,
故n=k+1时结论也成立
综上,由(i)、(ii)可知Sn=对所有正整数n都成立 ……10分
……10分
于是当n≥2时,an=Sn-Sn-1=-=,
又n=1时,a1==,所以
{an}的通项公式an=,n=1,2,3,… ……12分
……12分
本题难度较大,不过计算较易,数列的前面一些项的关系也比较容易发现
类型13双数列型
解法:根据所给两个数列递推公式的关系,灵活采用累加、累乘、化归等方法求解。
例:已知数列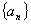 中,
中,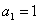 ;数列
;数列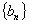 中,
中,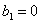 。当
。当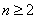 时,
时,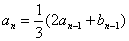 ,
,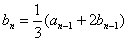 ,求
,求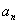 ,
,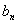 .
.
解:因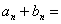
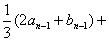
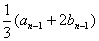
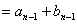
所以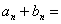

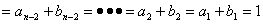
即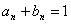 …………………………………………(1)
…………………………………………(1)
又因为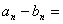
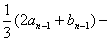


所以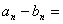
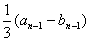
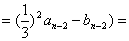 ……
……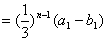
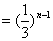 .即
.即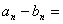
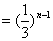 ………………………(2)
………………………(2)
由(1)、(2)得: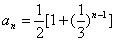 ,
, 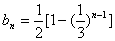
类型14周期型
解法:由递推式计算出前几项,寻找周期。
例:若数列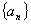 满足
满足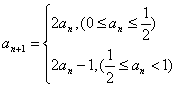 ,若
,若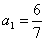 ,则
,则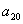 的值为___________。
的值为___________。
变式:(2005,湖南,文,5)
已知数列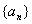 满足
满足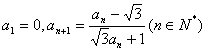 ,则
,则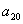 = ( )
= ( )
A.0 B.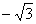 C.
C.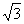 D.
D.