段考复习总结
3.1直线的倾斜角和斜率
3.1倾斜角和斜率
1、直线的倾斜角的概念:当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α= 0°.
2、 倾斜角α的取值范围: 0°≤α<180°. 当直线l与x轴垂直时, α= 90°.
3、直线的斜率:
一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα
⑴当直线l与x轴平行或重合时, α=0°, k = tan0°=0;
⑵当直线l与x轴垂直时, α= 90°, k 不存在.
由此可知, 一条直线l的倾斜角α一定存在,但是斜率k不一定存在.
4、 直线的斜率公式:
给定两点P1(x1,y1),P2(x2,y2),x1≠x2,用两点的坐标来表示直线P1P2的斜率:
斜率公式: k=y2-y1/x2-x1
3.1.2两条直线的平行与垂直 (理解)
1、两条直线都有斜率而且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,那么它们平行,即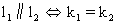
注意: 上面的等价是在两条直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不成立.即如果k1=k2, 那么一定有L1∥L2
2、两条直线都有斜率,如果它们互相垂直,那么它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,那么它们互相垂直,即
3.2.1 直线的点斜式方程 (理解)
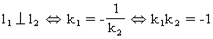 1、 直线的点斜式方程:直线
1、 直线的点斜式方程:直线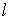 经过点
经过点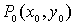 ,且斜率为
,且斜率为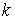
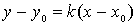
2、、直线的斜截式方程:已知直线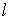 的斜率为
的斜率为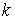 ,且与
,且与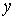 轴的交点为
轴的交点为
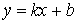
3.2.2 直线的两点式方程 (理解)
1、直线的两点式方程:已知两点 其中
其中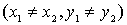 y-y1/y-y2=x-x1/x-x2
y-y1/y-y2=x-x1/x-x2
2、直线的截距式方程: 已知直线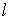 与
与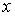 轴的交点为A
轴的交点为A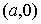 ,与
,与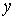 轴的交点为B
轴的交点为B ,其中
,其中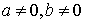
3.2.3 直线的一般式方程 (理解)
1、直线的一般式方程:关于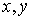 的二元一次方程
的二元一次方程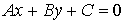 (A,B不同时为0)
(A,B不同时为0)
2、各种直线方程之间的互化。
3.3直线的交点坐标与距离公式 (重点)
 3.3.1 两直线的交点坐标 (理解,实际上是解方程)
3.3.1 两直线的交点坐标 (理解,实际上是解方程)
1、给出例题:两直线交点坐标
L1 :3x+4y-2=0 L1:2x+y +2=0
解方程组  得 x=-2,y=2
得 x=-2,y=2
所以L1与L2的交点坐标为M(-2,2)
3.3.2 两点间距离(直接背,实际上是勾股定理)
两点间的距离公式:
3.3.3 点到直线的距离公式(直接背)
1.点到直线距离公式:
点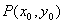 到直线
到直线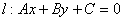 的距离为:
的距离为:
2、两平行线间的距离公式:
已知两条平行线直线 和
和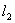 的一般式方程为
的一般式方程为 :
: ,
,
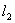 :
: ,则
,则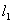 与
与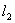 的距离为
的距离为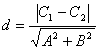 、
、
第四章 圆与方程
4.1.1 圆的标准方程
1、圆的标准方程:
圆心为A(a,b),半径为r的圆的方程
2、点 与圆
与圆 的关系的判断方法: (理解)
的关系的判断方法: (理解)
(1) >
>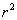 ,点在圆外 (2)
,点在圆外 (2) =
=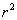 ,点在圆上
,点在圆上
(3) <
<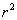 ,点在圆内
,点在圆内
4.1.2 圆的一般方程
1、圆的一般方程:
2、圆的一般方程的特点:
(1)①x2和y2的系数相同,不等于0. ②没有xy这样的二次项.
(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了.
(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显。
4.2.1 圆与圆的位置关系 (理解,记得点到直线距离公式是基础)
1、用点到直线的距离来判断直线与圆的位置关系.
设直线 :
: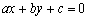 ,圆
,圆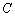 :
: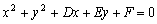 ,圆的半径为
,圆的半径为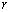 ,圆心
,圆心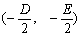 到直线的距离为
到直线的距离为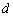 ,则判别直线与圆的位置关系的依据有以下几点:
,则判别直线与圆的位置关系的依据有以下几点:
(1)当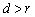 时,直线
时,直线 与圆
与圆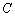 相离;(2)当
相离;(2)当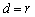 时,直线
时,直线 与圆
与圆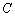 相切;
相切;
(3)当 时,直线
时,直线 与圆
与圆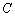 相交;
相交;
4.2.2 圆与圆的位置关系 (理解)
两圆的位置关系.
设两圆的连心线长为 ,则判别圆与圆的位置关系的依据有以下几点:
,则判别圆与圆的位置关系的依据有以下几点:
(1)当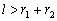 时,圆
时,圆 与圆
与圆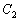 相离;(2)当
相离;(2)当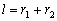 时,圆
时,圆 与圆
与圆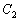 外切;
外切;
(3)当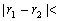
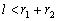 时,圆
时,圆 与圆
与圆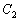 相交;
相交;
(4)当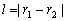 时,圆
时,圆 与圆
与圆 内切;(5)当
内切;(5)当 时,圆
时,圆 与圆
与圆 内含;
内含;
4.2.3 直线与圆的方程的应用
1、利用平面直角坐标系解决直线与圆的位置关系;
2、过程与方法
用坐标法解决几何问题的步骤:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
 第二步:通过代数运算,解决代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第二篇:直线与方程知识点总结与典型习题分类练习解析(精品)
卓越个性化教案学生姓名年级高一授课时间教师姓名课时GFJW0901
02直线与方程
【知识点】
(1)直线的倾斜角
定义:x轴正向与直线向上方向或重合时,我们规定它的倾斜角为0度。因此,倾斜角的取值范围是(2)直线的斜率
①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。直线的斜率常用k?tan?。斜率反映直线与轴的倾斜程度。
当直线l与x轴平行或重合时,α=0°,k=tan0°=0;当直线l与x轴垂直时,α=90°,k不存在.
当??0,90时,k?0;
在。????当??90,180????时,k?0;当??90时,k不存?
②过两点的直线的斜率公式:k?y2?y1(x1?x2)x2?x1(P1(x1,y1),P2(x2,y2),x1≠x2)
注意下面四点:(1)当x1?x2时,公式右边无意义,直线的斜率不存在,倾斜角为90°;
(2)k与P1、P2的顺序无关;
(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;
(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
注意:当直线的斜率为0°时,k=0,直线的方程是1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
y?kx?b,直线斜率为k,直线在y轴上的截距为b
Ax?By?C?0(A,B不全为0)
1各式的适用范围2特殊的方程如:○注意:○
x轴的直线:y?b(by轴的直线:(a(7)两条直线的交点
l1:A1x?B1y?C1?0l2:A2x?B2y?C2?0相交
A1x?B1y?C1?0交点坐标即方程组?的一组解。?Ax?By?C?022?2
方程组无解?l1//l2;方程组有无数解?
1l1与l2重合
卓越个性化教学讲义
(9一点P?x0,y0?到直线l1:Ax?By?C?0(10已知两条平行线直线l1和l2的一般式方程为l1:Ax?By?C1?0,
l2:Ax?By?C2?0,则l1与l2(11)直线系方程:即具有某一共同性质的直线
(一)平行直线系
平行于已知直线A0x?B0y?C0?0(A0,B0是不全为0的常数)的直线系:
A0x?B0y?C?0(C为常数)
(二)垂直直线系
垂直于已知直线A0x?B0y?C0?0(A0,B0是不全为0的常数)的直线系:
B0x?A0y?C?0(C为常数)
(三)过定点的直线系(ⅰ)斜率为k的直线系:(ⅱ)过两条直线l1为
y?y0?k?x?x0?,直线过定点?x0,y0?;
:A1x?B1y?C1?0,l2:A2x?B2y?C2?0的交点的直线系方程
,其中直线l2不在直线系中。?A1x?B1y?C1????A2x?B2y?C2??0(?为参数)
【课堂讲解与练习】
直线的方程
333
1.设a,b,c是互不相等的三个实数,如果A(a,a)、B(b,b)、C(c,c)在同一直线上,求证:a+b+c=0.证明∵A、B、C三点共线,∴kAB=kAC,
a3?b3a3?c3
∴,化简得a2+ab+b2=a2+ac+c2,?
a?ba?c
∴b-c+ab-ac=0,(b-c)(a+b+c)=0,
∵a、b、c互不相等,∴b-c≠0,∴a+b+c=0.
2.(2009·宜昌调研)若实数x,y满足等式(x-2)2+y2=3,那么
(A.
12
y
的最大值为x
22
)
B.
33
C.
32
D.答案D
3.(1)求经过点A(-5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程;(2)过点A(8,6)引三条直线l1,l2,l3,它们的倾斜角之比为1∶2∶4,若直线l2的方程是y=x,求
直线l1,l3的方程.
解(1)①当直线l在x、y轴上的截距都为零时,设所求的直线方程为y=kx,将(-5,2)代入y=kx中,得k=-,此时,直线方程为y=-x,即2x+5y=0.②当横截距、纵截距都不是零时,设所求直线方程为
2
yx
?=1,将(-5,2)代入所设方2aa
25
25
34
卓越个性化教学讲义程,解得a=-,此时,直线方程为x+2y+1=0.综上所述,所求直线方程为x+2y+1=0或2x+5y=0.3412(2)设直线l2的倾斜角为?,则tan?=.于是tan?2=1?cos?=sin?1?45?1,33
5
3
2tan?4?24,所以所求直线l的方程为y-6=1(x-8),?tan2?=1371?tan2?1?(3)2
42?
即x-3y+10=0,l3的方程为y-6=24(x-8),即24x-7y-150=0.7
4.直线l经过点P(3,2)且与x,y轴的正半轴分别交于A、B两点,△OAB的面积为12,求直线l的方程.
解方法一设直线l的方程为xy??1(a>0,b>0),ab
∴A(a,0),B(0,b),
?ab?24,?a?6,∴?解得??32?b?4.?a?b?1.?
∴所求的直线方程为?
方法二x6y=1,即2x+3y-12=0.4设直线l的方程为y-2=k(x-3),
2,令x=0,得直线l在y轴上的截距b=2-3k.k
2
3令y=0,得直线l在x轴上的截距a=3-??2?k?23∴?3??(2-3k)=24.解得k=-.∴所求直线方程为y-2=-(x-3).即2x+3y-12=0.
9.已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.
解方法一直线x+my+m=0恒过A(0,-1)点.
kAP=
则-?1?1?1?23=-2,kAQ==,0?10?22131≥或-≤-2,m2m
2
312∴-≤m≤且m≠0.又∵m=0时直线x+my+m=0与线段PQ有交点,∴所求m的取值范围是-≤m≤.
方法二过P、Q两点的直线方程为y-1=2?114(x+1),即y=x+,代入x+my+m=0,2?1332312
整理,得x=-7m7m.由已知-1≤-≤2,m?3m?3解得-≤m≤.2
312
两直线方程
2例1已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a-1=0,
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
3
卓越个性化教学讲义
解
(1)方法一当a=1时,l1:x+2y+6=0,l2:x=0,l1不平行于l2;当a=0时,l1:y=-3,l2:x-y-1=0,l1不平行于l2;当a≠1且a≠0时,两直线可化为l1:y=-x-3,l2:y=
a2
1
x-(a+1),1?a
1?a
???
l1∥l2??21?a,解得a=-1,
??3??(a?1)?
综上可知,a=-1时,l1∥l2,否则l1与l2不平行.方法二
由A1B2-A2B1=0,得a(a-1)-1×2=0,由A1C2-A2C1≠0,得a(a-1)-1×6≠0,
?a(a?1)?1?2?0
∴l1∥l2???2
??a(a?1)?1?6?0
2??a?a?2?0
???a=-1,
2?a(a?1)?6?
2
故当a=-1时,l1∥l2,否则l1与l2不平行.
(2)方法一
当a=1时,l1:x+2y+6=0,l2:x=0,l1与l2不垂直,故a=1不成立.
a112?a?
x-3,l2:y==-1?a=.x-(a+1),由???·21?a1?a3?2?
2
3
当a≠1时,l1:y=-方法二
由A1A2+B1B2=0,得a+2(a-1)=0?a=.
例3(12分)已知直线l过点P(3,1)且被两平行线l1:x+y+1=0,l2:x+y+6=0截得的线段长为5,求直线l的方程.
解方法一若直线l的斜率不存在,
则直线l的方程为x=3,此时与l1,l2的交点分别是A(3,-4),B(3,-9),截得的线段长|AB|=|-4+9|=5,符合题意.
若直线l的斜率存在时,则设直线l的方程为y=k(x-3)+1,分别与直线l1,l2的方程联立,由?
?y?k(x?3)?1?3k?21?4k?
,解得A?,?.
x?y?1?0k?1k?1???
8分
由?
?y?k(x?3)?1?3k?71?9k?
,解得B??,
?k?1k?1??x?y?6?0
2
2
由两点间的距离公式,得
?3k?23k?7??1?4k1?9k?
????+??=25,k?1??k?1k?1??k?1
解得k=0,即所求直线方程为y=1.
综上可知,直线l的方程为x=3或y=1.
方法二设直线l与l1,l2分别相交于A(x1,y1),B(x2,y2),则x1+y1+1=0,x2+y2+6=0,两式相减,得(x1-x2)+(y1-y2)=5①6分
22
又(x1-x2)+(y1-y2)=25②联立①②可得?
?x1?x2?5?x?x?0
或?12,
?y1?y2?0?y1?y2?5
10分
由上可知,直线l的倾斜角分别为0°和90°,
4
卓越个性化教学讲义故所求的直线方程为x=3或y=1.例4求直线l1:y=2x+3关于直线l:y=x+1对称的直线l2的方程.
解方法一由??y?2x?3
?y?x?1知直线l1与l的交点坐标为(-2,-1),
∴设直线l2的方程为y+1=k(x+2),即kx-y+2k-1=0.
在直线l上任取一点(1,2),由题设知点(1,2)到直线l1、l2的距离相等,
由点到直线的距离公式得
k?2?2k?1
1?k22=2?2?32?(?1)22,
解得k=(k=2舍去),∴直线l2的方程为x-2y=0.
方法二设所求直线上一点P(x,y),
则在直线l1上必存在一点P1(x0,y0)与点P关于直线l对称.
由题设:直线PP1与直线l垂直,且线段PP1的中点
?y0?y?x?x?1??1?x?y?1?x?x0y?y0??0P2?,变形得?0,?2,2??在直线l上.∴?y?x?1y?yx?x???0?00??1?2?212
代入直线l1:y=2x+3,得x+1=2×(y-1)+3,整理得x-2y=0.所以所求直线方程为x-2y=0.
分类例题解析
3.1直线的倾斜角与斜率
3.1.1倾斜角与斜率
【典型例题】
题型一求直线的倾斜角
例1已知直线lA.60°B.30°C.60°或120°D.30°或150°
变式训练:).
设直线l过原点,其倾斜角为?,将直线l绕原点沿逆时针方向旋转45°,得到直线l1,则l1的倾斜角为(
A.)。B.??45???135?C.135???
D.当0°≤α<135°时为??45?,当135°≤α<180°时,为??135?题型二求直线的斜率
例2如图所示菱形ABCD中∠BAD=60°,求菱形ABCD各边和两条对
角线所在直线的倾斜角和斜率.
变式训练:已知过两点A(m2?2,m2?3),B(3?m2?m,2m)的直线l的倾斜角为45°,求实数m的值.
5
卓越个性化教学讲义题型三直线的倾斜角与斜率的关系例

3右图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则().
A.k1<k2<k3B.k3<k1<k2C.k3<k2<k1D.k1<k3<k2
拓展一三点共线问题
例4已知三点A(a,2)、B(3,7)、C(-2,-9a)在一条直线上,求实数a的值.
变式训练:
若三点P(2,3),Q(3,a),R(4,b)共线,那么下列成立的是().
A.a?4,b?5B.b?a?1C.2a?b?3D.a?2b?3
拓展二与参数有关问题
例5已知两点A(-2,-3),B(3,0),过点P(-1,2)的直线l与线段AB始终有公共点,求直线l的斜率k的取值范围.
变式训练:
已知A(2,?3),B(?3,?2)两点,直线l过定点P(1,1)且与线段AB相交,求直线l的斜率k的取值范围.
拓展三利用斜率求最值
例6已知实数x、y满足2x?y?8,当2≤x≤3时,求y的最大值与最小值。x
变式训练:利用斜率公式证明不等式:a?ma?(0?a?b且m?0)b?mb
3.1.2两条直线平行与垂直的判定
【典型例题】
题型一两条直线平行关系
6
卓越个性化教学讲义
例1已知直线l1经过点M(-3,0)、N(-15,-6),l2经过点R(-2,
判断l1与l2是否平行?35)、S(0,),试22
变式训练:经过点P(?2,m)和Q(m,4)的直线平行于斜率等于1的直线,则m的值是(
A.4B.1C.1或3D.1或4
题型二两条直线垂直关系
例2已知?ABC的顶点B(2,1),C(?6,3),其垂心为H(?3,2),求顶点A的坐标.).变式训练:(1)l1的倾斜角为45°,l2经过点P(-2,-1)、Q(3,-6),问l1与l2是否垂直?
(2)直线l1,l2的斜率是方程x2?3x?1?0的两根,则l1与l2的位置关系是
题型三根据直线的位置关系求参数.
例3已知直线l1经过点A(3,a)、B(a-2,-3),直线l2经过点C(2,3)、D(-1,a-2),
(1)如果l1//l2,则求a的值;(2)如果l1⊥l2,则求a的值
题型四直线平行和垂直的判定综合运用
例4四边形ABCD的顶点为A(2,2?、B(?2,2)、C(0,2?、D(4,2),试判断四边形ABCD的形状.
变式训练:已知A(1,1),B(2,2),C(3,-3),求点D,使直线CD⊥AB,且CB∥AD.探点一数形结合思想
例5已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上.(2)当BC平行于x轴时,求点A的坐标.
7
卓越个性化教学讲义
探点二分类讨论思想
例6?ABC的顶点A(5,?1),B(1,1),C(2,m),若?ABC为直角三角形,求m的值.
3.2直线的方程
3.2.1直线的点斜式方程
【典型例题】
题型一求直线的方程
例1写出下列点斜式直线方程:(1)经过点A(2,5),斜率是4;(2)经过点B(3,?1),倾斜角是30?.
例2倾斜角是135?,在y轴上的截距是3的直线方程是.
变式训练:
1.已知直线l过点P(3,4),它的倾斜角是直线y?x?1的两倍,则直线l的方程为
2.已知直线l在y轴上的截距为-3,且它与两坐标轴围成的三角形的面积为6,求直线l的方程.
3.将直线y?x?1绕它上面一点(1,)沿逆时针方向旋转15°,得到的直线方程是.
题型二利用直线的方程求平行与垂直有关问题
例3已知直线l1的方程为y??2x?3,l2的方程为y?4x?2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程。
探究一直线恒过定点或者象限问题
例4.已知直线y?kx?3k?1.
(1)求直线恒经过的定点;
(2)当?3?x?3时,直线上的点都在x轴上方,求实数k的取值范围.
8
卓越个性化教学讲义
探究二直线平移
例5已知直线l:y=2x-3,将直线l向上平移2个单位长度,再向右平移4个单位后得到的直线方程为__________________
3.2.2直线的两点式方程
【典型例题】
题型一求直线方程
例1已知△ABC顶点为A(2,8),B(?4,0),C(6,0),求过点B且将△ABC面积平分的直线方程.
变式训练:
1.已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是().
A.4x?2y?5B.4x?2y?5C.x?2y?5D.x?2y?5
2.已知2x1?3y1?4,2x2?3y2?4,则过点A(x1,y1),B(x2,y2)的直线l的方程是().
A.2x?3y?4B.2x?3y?0C.3x?2y?4D.3x?2y?0
例2求过点P(3,2),并且在两轴上的截距相等的直线方程.
变式训练:已知直线l过点(3,-1),且与两轴围成一个等腰直角三角形,则l的方程为题型二直线方程的应用
例3长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李费用y(元)是行李重量x(千克)的一次函数,其图象如图所示.
(1)求y与x之间的函数关系式,并说明自变量x的取值范围;
(2)如果某旅客携带了75千克的行李,则应当购买多少元行李票?
(千克)
探究一直线与坐标轴围成的周长及面积
例4已知直线l过点(?2,3),且与两坐标轴构成面积为4的三角形,求直线l的方程.探究二有关光的反射
例5光线从点A(-3,4)发出,经过x轴反射,再经过y轴反射,光线经过点B(-2,
6),求射入y轴后的反射线的方程.
9
卓越个性化教学讲义
变式训练:已知点A(?3,8)、B(2,2),点P是x轴上的点,求当AP?PB最小时的点P的坐标.
3.2.3直线的一般式方程
【典型例题】
题型一灵活选用不同形式求直线方程
例1根据下列各条件写出直线的方程,并且化成一般式:
1(1)斜率是-,经过点A(8,-2);(2)经过点B(4,2),平行于x轴;2
3(3)在x轴和y轴上的截距分别是,-3;(4)经过两点P、P2(5,-4).1(3,-2)2
题型二直线不同形式之间的转化
例2求出直线方程,并把它化成一般式、斜截式、截距式:过点A(?5,6),B(?4,8).题型三直线一般式方程的性质
例3直线方程Ax?By?C?0的系数A、B、C分别满足什么关系时,这条直线分别有以下性质?
(1)与两条坐标轴都相交;(2)只与x轴相交;(3)只与y轴相交;(4)是x轴所在直线;(5)是y轴所在直线.
变式训练:已知直线l:5ax?5y?a?3?0。
(1)求证:不论a为何值,直线l总经过第一象限;(2)为使直线不经过第二象限,求a的取值范围。
题型四运用直线平行垂直求参数
例4已知直线l1:x?my?2m?2?0,l2:mx?y?1?m?0,问m为何值时:
(1)l1?l2;(2)l1//l2.
10
卓越个性化教学讲义
变式训练:(1)求经过点A(3,2)且与直线4x?y?2?0平行的直线方程;
(2)求经过点B(3,0)且与直线2x?y?5?0垂直的直线方程.
题型五综合运用
例5已知直线l1:x?my?6?0,l2:(m?2)x?3y?2m?0,求m的值,使得:
(1)l1和l2相交;(2)l1⊥l2;(3)l1//l2;(4)l1和l2重合.
3.3直线的交点坐标与距离公式
3.3.1两直线的交点坐标
3.3.2两点间的距离
【典型例题】
题型一求直线的交点坐标
例1判断下列各对直线的位置关系.如果相交,求出交点坐标.
(1)直线l1:2x-3y+10=0,l2:3x+4y-2=0;(2)直线l1:nx?y?n?1,l2:ny?x?2n.题型二三条直线交同一点
例2若三条直线2x?3y?8?0,x?y?1?0,kx?y?2?0相交于一点,则k的值等于变式训练:1.设三条直线:x?2y?1,2x?ky?3,3kx?4y?5交于一点,求k的值
2.试求直线l1:x?y?2?0关于直线l2:3x?y?3?0对称的直线l的方程.
题型三求过交点的直线问题
例3求经过两条直线2x?y?8?0和x?2y?1?0的交点,且平行于直线4x?3y?7?0的直线方程.
11
卓越个性化教学讲义
变式训练:已知直线l1:2x-3y+10=0,l2:3x+4y-2=0.求经过l1和l2的交点,且与直线l3:3x-2y+4=0垂直的直线l的方程.
题型四两点间距离公式应用
例4已知点A(?2,?1),B(a,3)且|AB|?5,则a的值为
变式训练:
在直线2x?y?0上求一点P,使它到点M(5,8)的距离为5,并求直线PM的方程.题型五三角形的判定
例5已知点A(1,2),B(3,4),C(5,0),判断?ABC的类型.
探究一直线恒过定点问题
例6已知直线(a?2)y?(3a?1)x?1.求证:无论a为何值时直线总经过第一象限.
变式训练:若直线l:y=kx2x+3y-6=0的交点位于第一象限,求直线l的倾斜角的取值范围.
探究二利用对称性求最值问题(和最小,差最大)
例7直线2x-y-4=0上有一点P,求它与两定点A(4,-1),B(3,4)的距离之差的最大值.
12
卓越个性化教学讲义
变式训练:已知M(1,0)、N(?1,0),点P为直线2x?y?1?0上的动点.求PM2?PN2的最小值,及取最小值时点P的坐标.
3.3.3点到直线的距离
3.3.4两条平行直线间的距离
拓展:点关于点、直线对称点的求法
【典型例题】
题型一利用点到直线距离求参数
例1已知点(a,2)(a?0)到直线l:x?y?3?0的距离为1,则a=(
ABC?1
题型二利用点到直线距离求直线的方程D?1).
110例2求过直线l1:y??x?和l2:3x?y?0的交点并且与原点相距为1的直线l的方程.33
变式训练:
直线l过点P(1,2),且M(2,3),N(4,-5)到l的距离相等,则直线l的方程是题型三利用平行直线间的距离求参数
例3若两平行直线3x?2y?1?0和6x?ay?c?0之间的距离为c?2,求的值.13a变式训练:两平行直线5x?12y?3?0与10x?24y?5?0间的距离是(
A.).2
13B.1
13C.1
26D.5
26
题型四利用平行直线间的距离求直线的方程
例4与直线l:5x?12y?6?0平行且与l的距离2的直线方程是
13
卓越个性化教学讲义
题型五点、直线间的距离的综合运用
例5已知点P到两个定点M(-1,0)、N(1,0,点N到直线PM的距离为1.求直线PN的方程.
探究一
例6与直线有关的对称问题△ABC中,A(3,3),B(2,?2),C(?7,1).求∠A的平分线AD所在直线的方程.变式训练:1.与直线2x?3y?6?0关于点(1,-1)对称的直线方程是
2.求点A(2,2)关于直线2x?4y?9?0的对称点坐标
探究二与距离有关的最值问题
例7在函数y?4x2的图象上求一点P,使P到直线y?4x?5的距离最短,并求这个最短的距离.
变式训练:在直线l:3x?y?1?0上求一点P,使得:
(1)P到A(4,1)和B(0,4)的距离之差最大。
(2)P到A(4,1)和C(3,4)的距离之和最小。
14
卓越个性化教学讲义
【作业】
一.选择题
1.(安徽高考)过点(1,0)且与直线x-2y=0平行的直线方程是(A.x-2y-1=0B.x-2y+1=0C.2x+y-2=0D.x+2y-1=02.A.
过点P(?1,3)且垂直于直线x?2y?3?0的直线方程为(
)
)
D.
2x?y?1?0
B.
2x?y?5?0
C.
x?2y?5?0
x?2y?7?0
3.A.
已知过点A(?2,m)和B(m,4)的直线与直线2x?y?1?0平行,则m的值为(
)
B.
?8
C.
2
D.
10
)
4.(安徽高考)直线过点(-1,2),且与直线2x-3y+4=0垂直,则直线的方程是(A.3x+2y-1=0
B.3x+2y+7=0
C.2x-3y+5=0
D.2x-3y+8=0
(
)
5.设直线ax+by+c=0的倾斜角为?,且sin??cos??0则a,b满足A.a+b=1
B.a-b=1
C.a+b=0
D.a-b=0C、?3
2
6.如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a=A、-3
B、-6
D、2
3
7.点P(-1,2)到直线8x-6y+15=0的距离为(A2
B1
2
C1
D
72
)
8.直线mx-y+2m+1=0经过一定点,则该点的坐标是A(-2,1)
B(2,1)
C(1,-2)
D(1,2)
9.(上海文,15)已知直线l1:(k?3)x?(4?k)y?1?0,与l2:2(k?3)x?2y?3?0,平行,则k得值是(A.
1或3
)B.1或5
C.3或5
D.1或2
10、若图中的直线L1、L2、L3的斜率分别为K1、K2、K3A、K1﹤K2﹤K3B、K2﹤K1﹤K3C、K3﹤K2﹤K1
D、K1﹤K3﹤K2
)L3
L2
xL1
11.(北京卷)“m=的(
)
1
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”2
(B)充分而不必要条件(D)既不充分也不必要条件
)
(A)充分必要条件(C)必要而不充分条件
12、与直线2x+3y-6=0关于点(1,-1)对称的直线是(
A.3x-2y-6=0B.2x+3y+7=0
15
卓越个性化教学讲义C.3x-2y-12=0D.2x+3y+8=0)
C.ab<0,bc>0D.ab13.若直线ax+by+c=0在第一、二、三象限,则(A.ab>0,bc>0
<0,bc<0
14.(北京文)“m=B.ab>0,bc<01”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”2
()
B.充分而不必要条件
D.既不充分也不必要条件的A.充分必要条件C.必要而不充分条件
15.如果直线l经过两直线2x-3y+1=0和3x-y-2=0的交点,且与直线y=x垂直,则原点到直线l的距离是(
A.2B.1)C.
)2D、2216.原点关于x-2y+1=0的对称点的坐标为(
2??4A.?, -?5??5
二、填空题
1.?24?B.?-, ?55???42?C.?, ?55??4??2D.?, -?5??5点P(1,?1)到直线x?y?1?0的距离是________________.
2.已知A(-4,-6),B(-3,-1),C(5,a)三点共线,则a的值为()
3.经过两直线11x+3y-7=0和12x+y-19=0的交点,且与A(3,-2),B(-1,6)等距离
的直线的方程是。
4.(全国Ⅰ文16)若直线m被两平行线l1:x?y?1?0与l2:x?y?3?0所截得的线段的长为22,则m的倾斜角可以是①15
其中正确答案的序号是
三.解答题
1.已知两条直线l1:x?1?m?y?2?m,l2:2mx?4y??16.
(1)相交
2.(2)平行(3)垂直?②30?③45?④60?⑤75?.(写出所有正确答案的序号)?m为何值时,l1与l2:求经过直线l1:2x?3y?5?0,l2:3x?2y?3?0的交点且平行于直线2x?y?3?0的直线方程.
3.求平行于直线x?y?2?0,且与它的距离为16
卓越个性化教学讲义
4.已知直线l1:mx+8y+n=0与l2:2x+my-1=0互相平行,求l1,l2之间的距离为时的直线l1的方程.
5.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点。
(1)求AB边所在的直线方程;(2)求中线AM的长(3)求AB边的高所在直线方程。
6.求与两坐标轴正向围成面积为2平方单位的三角形,并且两截距之差为3的直线的方程。
7.(本题12分)经过点A(3,0)且与直线2x+y-5=0垂直的直线方程。
8.(本题12分)已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x-3y+16=0,CA:2x+y-2=0
求AC边上的高所在的直线方程.
9.(本题12分)已知?ABC的顶点A(0,1),AB边上的中线CD所在的直线方程为2x?2y?1?0,AC边上的高BH所在直线的方程为y?0.求?ABC的顶点B、C的坐标;
10.(本题14分)过点(2,3)的直线L被两平行直线L1:2x-5y+9=0与
L2:2x-5y-7=0所截线段AB的中点恰在直线x-4y-1=0上,求直线L的
方程
17
卓越个性化教学讲义
11.(本题14分)过点P(4,1)作直线l分别交x轴的正半轴和y轴的正半轴于点A、B,
当?AOB(O为原点)的面积S最小时,求直线l的方程,并求出S的最小值12求经过点A(?2,2)并且和两个坐标轴围成的三角形的面积是1的直线方程
13.一直线被两直线l1:4x?y?6?0,l2:3x?5y?6?0截得线段的中点是P点,当P点为(0,0)14.把函数y?f?x?在x?a及x?b之间的一段图象近似地看作直线,设a?c?b,
证明:f?c?的近似值是:f?a?c?af?b??f?a????a15.直线y??x?1和x轴,y轴分别交于点A,B,在线段AB为边在第一象限内作等3
1
2边△ABC,如果在第一象限内有一点P(m,使得△ABP和△ABC的面积相等,
求m的值
18
