离散数学实验报告（1）

 实验名称：构造任意合式公式的真值表

  

姓名：卢松

指导老师：冯伟森

年级：11级2班

学号：1143041172

学院：计算机

1、          功能

给出任意变元的合式公式，构造该合式公式的真值表。

1、      基本思想

仍然以用数值变量表示命题变元为前提规范，合式表示的表示。程序计算前将转换后的合式公式输入到本程序首个sign：语句后的条件位置上。另外使用a[N]来表示合式公式中所出现的n个命题变元。

一位数组a[N]除了表示n个命题变元外，它还是一个二进制加法的模拟器，每当在这个模拟器中产生一个二进制数时，就相当于给各命题变元产生了一组真值指派。其中数值一表示真值为1，数值0表示真值为0.

2、      算法逻辑

（1）            将二进制加法模拟器a[N]赋初值，a_i=0(i=1,2,…,n)。

（2）            计算模拟器中所对应于模拟器所给出的一组真值指派下合式公式的真值。（条件语句）

（3）            输出真值表中对应于模拟器所给出的一组真值指派及这组真值指派所对应的一行真值。

（4）            在模拟器a[N]中，模拟产生下一个二进制数值。

（5）            若a[N]中的数值等于2ⁿ，则结束，否则转（2）。

3、      源程序

#include<stdio.h>

#define N 4

main()

{

  int a[N];

  int i,z;

  printf("构造任意公式的真值表");

  printf("\n");

  for(i=1;i<=4;i++)

  {

         a[i]=0;

         printf("a[%d]=0  ",i);

  }

sign:

  if(!(a[1]==1||a[2]==1)&&((a[1]==1||a[3]==1)||a[4]==1))

         z=1;

  else

         z=0;

  for(i=N;i>=1;i--)

         printf("%4d",a[i]);

    printf("   |%4d\n",z);

         i=1;

sing:

         a[i]=a[i]+1;

         if(a[i]<2)

                goto sign;

         else

                a[i]=0;

         i++;

         if(i<=4)

                goto sing;

}

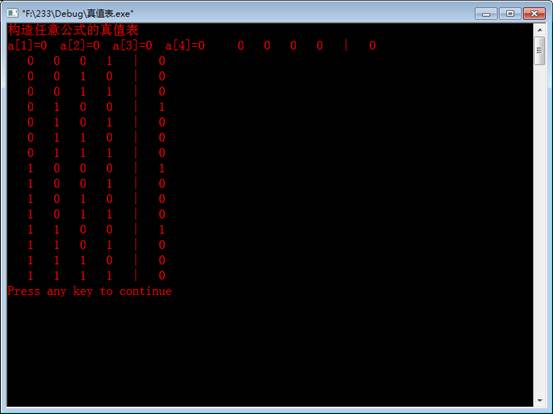
备注：本题是以~（PνQ）Λ((PνR)νS)为例子进行实验的。

4、   实验总结：

由于自己的技术问题只是验证了一组数据，因为时间紧迫所以来不及修改，课后会继续修改。从这次实验中学习到了很多，尤其是对真值表的判断条件，同时感觉到想像和实际操作之间的距离。

第二篇：四川大学出版编的离散数学课后习题答案

习题参考解答

习题1.1

1、（3）P：银行利率降低

Q：股价没有上升

P∧Q

（5） P：他今天乘火车去了北京 Q：他随旅行团去了九寨沟 P?Q

（7） P：不识庐山真面目

Q：身在此山中

Q→P，或 ～P→～Q

（9） P：一个整数能被6整除

Q：一个整数能被3整除

R：一个整数能被2整除

T：一个整数的各位数字之和能被3整除 P→Q∧R ，Q→T

2、（1）T （2）F （3）F （4）T

（6）T （7）F （8）悖论 习题 1.3

1（3）

P?(Q?R)??P?(Q?R)?(?P?Q)?(?P?R)?(P?Q)?(P?R)

1 5）F （

（4）

(P?Q)?(Q?R)?(R?P)?((P?R)?Q)?(R?P)

?((P?R)?(R?P))?(Q?(R?P)) ?(P?R)?(P?R)?(Q?R)?(Q?P)

?右

2、不， 不， 能

习题 1.4

1、(3) P?(R?(Q?P))?~P?(R?(~Q?P))

?(~P?R)?(T)?~P?R?(~P?R?(~Q?Q))

?(~P?R?~Q)?(~P?R?Q)

主合取范式

P?(R?(Q?P)

??P?(R?(?Q?P))

??P?(R??Q)?(R?P))

?(?P?(?Q?Q)?(?R?R)?(R??Q?(?P?P))?(R?P?(?Q?Q))?(?P??Q??R)?(?P?Q??R)?(?P??Q?R)?(?P??Q?R)? (R??Q??P)?(R??Q?P)?(R?P??Q)?(R?P?Q)?(?P??Q??R)?(?P?Q??R)?(?P??Q?R)?

(R??Q??P)?(R??Q?P)?(R?P?Q)

————主析取范式

2、(2) (P?Q)?(P?R)?(~P?Q)?(~P?R)

?(~P?Q?(~R?R))?(~P?R?(~Q?Q))

?(~P?Q?~R)?(~P?Q?R)?(~P?R?~Q)

P?(Q?R)?~P?(Q?R)

?(~P?Q)?(~P?R) ?(~P?Q?~R)?(~P?Q?R)?(~P?R?~Q)

?等价

3、解：根据给定的条件有下述命题公式：

（A→（C?D））∧～（B∧C）∧～（C∧D）

?（～A∨（C∧～D）∨（～C∧D））∧（～B∨～C）∧（～C∨～D） ?（（～A∧～B）∨（C∧～D∧～B）∨（～C∧D∧～B）∨

（～A∧～C）∨（C∧～D∧～C）∨（～C∧D∧～C））∧（～C∨～D） 2

?（（～A∧～B）∨（C∧～D∧～B）∨（～C∧D∧～B）∨

（～A∧～C）∨（～C∧D∧～C）） ∧（～C∨～D）

?（～A∧～B∧～C）∨（C∧～D∧～B∧～C）∨（～C∧D∧～B∧～C）∨ （～A∧～C∧～C）∨（～C∧D∧～C∧～C）∨（～A∧～B∧～D）∨

（C∧～D∧～B∧～D）∨（～C∧D∧～B∧～D）∨（～A∧～C∧～D）∨ （～C∧D∧～C∧～D）（由题意和矛盾律）

?（～C∧D∧～B）∨（～A∧～C）∨（～C∧D）∨（C∧～D∧～B）

?（～C∧D∧～B∧A）∨ （～C∧D∧～B∧～A）∨ （～A∧～C∧B）∨ （～A∧～C∧～B）∨ （～C∧D∧A）∨ （～C∧D∧～A）∨

（C∧～D∧～B∧A）∨（C∧～D∧～B∧～A）

?（～C∧D∧～B∧A）∨ （～A∧～C∧B∧D）∨ （～A∧～C∧B∧～D）∨ （～A∧～C∧～B∧D）∨ （～A∧～C∧～B∧～D）∨

（～C∧D∧A∧B）∨ （～C∧D∧A∧～B）∨ （～C∧D∧～A∧B）∨ （～C∧D∧～A∧～B）∨（C∧～D∧～B∧A）∨（C∧～D∧～B∧～A） ?（～C∧D∧～B∧A）∨ （～A∧～C∧B∧D）∨ （～C∧D∧A∧～B）∨ （～C∧D∧～A∧B） ∨（C∧～D∧～B∧A）

?（～C∧D∧～B∧A）∨ （～A∧～C∧B∧D）∨（C∧～D∧～B∧A） 三种方案：A和D、 B和D、 A和C

习题 1.5

1、 （1）需证(P?Q)?(P?(P?Q))为永真式

(P?Q)?(P?(P?Q))?~(~P?Q)?(~P?(P?Q))

~P?P?~(~P?Q)?(()?(~P?Q)) T

?~(~P?Q)?(~P?Q)?T

?P?Q?P?(P?Q)

（3）需证P??P?R?S为永真式

?P??P?R?S?F?R?S?F?S?T

?P??P?R?S

3

3、A?B?A?B为永真式。即~A?B永真

~A?B?B?~A?~B?~A永真

?A?B当且仅当~B?~A

4、设： P：珍宝藏在东厢房

Q：藏宝的房子靠近池塘

R：房子的前院栽有大柏树

S：珍宝藏在花园正中地下

t：后院栽有香樟树

m：珍宝藏在附近（后院）

命题化后进行推理：

(Q?~p)?(R?P)?Q?(R?S)?(t?m)

?~p?(R?P)?(R?S)?(t?m)

?~R?(R?S)?(t?m)

?S?(t?m)

即S为真，珍宝藏在花园正中地下

5、(1)F (P=0,Q=1) (2)F (P=1,Q=R=0) (3)F (P=0,Q=1) 习题 1.6

1.（1）~P?Q,R?~Q?P?~R

证：利用CP规则

① P P(附加前提)

② ~P?QP

③ QT①②I

④ R?~QP

4

⑤ ~RT③④I

⑥ 结论成立 CP规则①⑤

（2） (P?Q)?(R?S),(SVE?)证：① PP(附加) ?B?P B

② P∨Q T①

③ (P?Q)?(R?S)

④ R?S

⑤ S PT②③ T④

⑥ S∨E T⑤

⑦ S∨E→B P

⑧ B

⑨ P?BT⑥⑦ CP(①⑧)

2. (2) P：无任何痕迹

Q：失窃时，小花在OK厅 R：失窃时，小英在OK厅 S：失窃时，小胖在附近 T：金刚是偷窃者

M：瘦子是偷窃者

命题可符号化为：

{P, Q?R, S??P, Q?T, ?S??R, R?M} 证：①

②

P P P S?~P 5

③

④

⑤

⑥

⑦

⑧

⑨ ~S T①② ~S?~R P T③④ P T⑤⑥ P ~R Q?R Q Q?T T T⑦⑧ ∴金刚是窃贼。

3. (1) 不相容

(2) 相容 ?P?1,R?Q?S?0?

（3）不相容

（4）不相容

4. (1)证：?P?~Q???R?S???S?~Q??(P?Q)?P

??~P?~Q???R?S???~S?~Q???~P?Q??P 即 ???~P?~Q, R?S, ~S?~Q, ~P?Q, P? 利用消解原理：

① P P

②

③

④

⑤ ~P?~Q P ~Q ①② ~P?Q P ~P ③④

⑥ ~P?P?F □ ①⑤ 6

习题 2.1

1. (1)A?x?：x是实数 B?x?：x是有理数 ??x??B?x??A?x?????x?A?x??B?x????x?A?x??B?x??

(2)A?x?：x是直线

F?x,y?：x与y平行 G?x,y?：x与y相交 ?a?b?A?a??A?b???F?a,b???G?a,b???

(3)A(x)：x是会员 C(x)：x有意义 F(x,y)：x参加y a：这个活动 C?a???x?A?x??F?x,a??

或者 ??x(A?x??F?x,a?)??C?a?

（4） A?x?：x是正整数 B(x)：x是合数 C(x)：

?x?A?x??B?x??C?x??

（5） A?x?：x是人 B（x）：x存钱 a：利息

P:存钱有利息 F?x,y?：x想有y

?x??A?x??B?x??F?x,a?????P?A?x???B?x???

2.(1)P?0??P?1??P?2???R?0??R?1??Q?2??

(2)?P?0??Q?0????P?1??Q?1????P?2??Q?2?

4.(1) ??x???y??P?x,y??Q?y,t?????z?R?x,y,z? 7 x是质数

习题 2.2

1.（1）D：数 A?x?:x?0f?x,y??xy

?x?y?A?f?x,y???A?x??A?y????A?x?1???A?f?x?1,x?1??

可满足式

(2)A?x?:x是诚实的人 B?x?:x讲实话 a：小林

?x?A?x??B?x????A?a???B?a?

可满足式

(3) A?x?:x不便宜

F?x,y?:x买的y B?x?:x是好货 a：衣服 b：小王

?x?A?x??B?x??? F?a,b??A?a??B?a?

可满足式

（4）A?x?:x是作家 B?x?:x懂得人性本质

C?x?:x是诗人 D?x?:x是真正的

E?x?:x能刻画人们内心世界

F?x?:x很高明 P?x,y?:x创作了y

a：莎士比亚 b：哈姆雷特

?x??A?x??B?x??F?x????C?x???E(x)??D?x????P?a,b? ??(?x)?A(x)??B(x)?E(x)???x?C(x)?P(x,b)?D(x)?

2.(1) T

3.(1) F (2) T

实数 P(x,y):y?ex, Q(y):y?0 4. D:

习题 2.3

1.（1）?x?y?P?x??Q?y??

8

??x?y?~P?x??Q?y??

??x??y~P?x???yQ?y??

??x~P?x???yQ(y)

?~?xP?x???yQ(y)

??Ax?P?x????y?Q(y)

2. 不成立 P(0)P(1)P(2)Q(0)Q(1)Q(2),,,,D={0,1,2} 010101

3.(1)~???x?P?x????y?P?y??

?~?~??x?P?x????y?P?y??

?~???x??~P?x????y?P?y??

???x?P?x????y??~P?y??

???x???y??P?x??~P?y?? ——skolem范式

(2)~???x?P?x????y???z?Q?y,z??

?~?~??x?P?x????y???z?Q?y,z??

???x?P?x????y???z?~Q?y,z?

???x???y???z??P?x??~Q?y,z?? ——前束范式 ???x???y??P?x??~Q?y,f?x,y??? ——skolem范式 9

习题 2.4

1. （1）证：在某个解释下，??x???y??P?x??Q(y)?取值1，必有a,b?D, P?a??Q?b?，取值1，因此，?a?D P?a?取值1。 ???x?P?x?取值1，由定义，蕴含关系成立。

（2）①~???x?P?x??Q?a???~??x?P?x??~Q?a? ???x?P?x??~Q?a?

(2) 证: 在某个解释下，~???x?P?x??Q?a??取值1 即??x?P?x??Q?a?取值0，分二种情况： i)??x?P?x??0，则无论Q?a?为何值，??x?P?x??~Q?a?取值1。 ii) Q?a??0??x?P?x??1，则??x?P?x??~Q?a?取值1 由定义，蕴含关系成立。

10

习题 2.5

1（2）（反证法）

①~??x??P?x??Q?x?? P ②??x??P?x??Q?x?? T①,E ③??x??~?~P?x???Q?x?? T②,I ④??x??P?x??~Q?x?? T③,I ⑤P?x??~Q?x? US④ ⑥P?x? T⑤,I ⑦??x?P?x? UG⑥ ⑧??x?P?x????x?Q?x? P ⑨??x?Q?x? T⑧,I ⑩~Q?x? T⑤,I 11Q?x? US⑨ ○

12□ T⑩11I ○○

2. (1) 错误，应换元，即

①??x?P?x??Q?x?，

②P?y??Q?x?

（2） 正确

（3） 错误，a、b应是同一个常元

（4） 错误，因为在P?x????x?[Q?x??R(x)] 中x并不是自由出现

(5) 错误，因为在??x?P?x??Q?x?中，前件是命题，

而后件不是命题

11

（6） 错误，因为a、b并不是同一个常量

（7） 错误，①②和③④的顺序不对

应先使用ES，再使用US

3(1)解：设F(x,y):x≥y; G(z):z≥0 ; f(x,y)=x-y 前提：

① ?(x)?(y)（F(x,y)→G(f(x,y))

② ?(x)?(y)（?F(x,y)→?G(f(x,y))

③ ?(x)?(y)(?G(f(x,y)→ G(f(y,x)))

结论： ?(x)?(y)（G(f(x,y))∨G(f(y,x))） 证明（反证法）：

① ? ?(x)?(y)（G(f(x,y))∨G(f(y,x))）

② （?ｘ）（?ｘ）?（G(f(x,y))∨G(f(y,x))） ③ ?G(f(a,b))∧ ?G(f(b,a))

④ ?(x)?(y)（F(x,y)→G(f(x,y))

⑤ F(a,b)→G(f(a,b))

⑥ ?G(f(a,b))→?F(a,b)

⑦ ?(x)?(y)(?G(f(x,y)→ G(f(y,x)))

⑧ ? G(f(b,a))→G(f(a,b))

⑨ ?(x)?(y)（?F(x,y)→?G(f(x,y))

⑩ ?F(a,b)→?G(f(a,b))

⑾ G(f(a,b)) → F(a,b)

⑿ ?F(a,b) ∧ F(a,b)

12

4. （2）

证：首先，将结论否定否作为前提加入到原有前提中 ????x?P?x????x???P?x??Q?x??R?x???????x?P?x????x?Q?x?? ~??x???y??R?x??R?x??

????x?~P?x????x??~?P?x??Q?x???R?x??????u?P?u????v?Q?v?? ~??w???y??R?w??R?y??

???x???u???v???w???y???~P?x??R?x????~P?x??~Q?x??R?x??? ?P?u??R?u???~R?w??~R?w???

???x???w???y???~P?x??R?x????~P?x??~Q?x??R?x???P?a??Q?b?? ??~R?w??~R?y??? Skolem 范式

子句集为?~P?x??R?x?,~P?x??~Q?x??R?x?,P?a?,R?b?,~R?w??~R?y?? ①~P?x??R?x?

②P?a?

③R?x? ①,②代换{a/x}

④R?c? ③代换{c/x}

⑤~R?w??~R?y?

⑥~R?y? ④,⑤代换{c/w}

⑦~R?c? ⑥代换{c/y}

⑧□

13

习题 3.4 3、

(1)x?2A?2B?x?2A或x?2B

?x?A或x?B?x?A?B ?x?2A?B等号成立的条件为：A?B??（2）“?”x?2A?2B?x?2A和x?2B?x?A和x?B?x?A?B?x?2A?B

“?”如x?2A?B，由于上述过程可逆?x?2A?2B

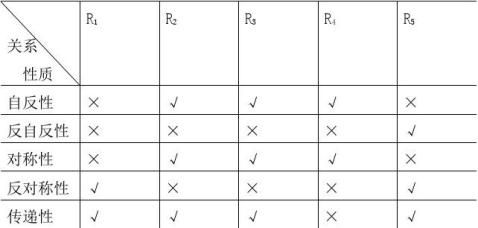
习题 5.2 2.

习题 5.3

2. （3）“?”R是对称的，设

??y,x??R?1

x,y?R则 y,x?R

?x,y?R?1

??x,y??R??y,x??R，即R?1?R

?x,y?R，由R

?1

“?” R?R?1

的定义，y,x?R?1

?y,x?R，即R是对称的。

（5）“?”R是传递的，对??x,z??R2

14

?y?A ??x,y??R?y,z??R

即R2?R

“?”R2?R，，对??x,y??R有?x,z??R2?R

??x,z??R

?y,z??R，由R的定义，

2

??x,z??R，即R是可传递的。

4. 解：?R?R1?R2，且R1?R2??

?Rm?Rm1?Rm2

3?R1?IA1

5

R2?IA2,

A?A1?A2

?需3|m，5|m

?m?15，即 n?16

1616

R16?R1?R2?R1?R2?R

故使R

m

?Rn的最小正整数m?1,

n?16

习题 5.4 2、解：

?0

??0?1??0MR??

?0?0??0?0?

1000000001000000000000010 0000001

0000100000000100

?

?0?

??111000?

?11100

?0???000110?M?

?t(R)?000110??

?000110?

??000111??

?000110???

?

?111000

001111100011111

0??0?0??1?? 1?1??1?1??

i

R3. (3)证：?t(R1)?iU?11

t(R1?R2)?U(R1?R2)i

i?1?

i

t(R2)?UR

i?12

由归纳法可证：对? i?N

?

ii

R?R?(R1?R2)i 12

15

???i???i??ii???UR??U(R?R)?U(R1?R2)i?t(R1?R2) ?t(R1)?t(R2)??UR?i?11??i?12?i?112i?1????

(4)证：①?R

?????R??R?t(R)?URi i?1???R?

?R?????t?R???U?t?R??j ?j?1?由归纳法可证：?j?N?????j??t?R??j?t?R? ?U?t?R???U?t?R???t?R??R? j?1j?1

③R?R??R??R??IA?t?R? ?R?R??R??IA?t?R???R?IA?R?t?R? ?R?R?t?R??t?R??R?

习题 5.5

1. 证：?A???a,b?|a,b?N?? R????a,b?,?c,d??|ad?bc?

①自反性 由A的定义，ab?ba?a,b?N ??a,b?,?a,b???R

②对称性 设??a,b?,?c,d???R，则ad?bc 即 cb?da???c,d?,?a,b???R ③传递性 设??a1,b1?,?c1d1???R，则a1d1?b1c1 ??c1,d1?,?c2d2???R，则c1d2?d1c2

?a1d1d2?b1c1d2?b1d1c2

??a1d2?b1c2 ??a1,b1?,?c2,d2???R

3. 解：?A??1,2,3,4,?, S0???1,2,4?,?3?? 16

设A1??1,2,3,4?,A2??3?

?1，?1，?2，?2，?4，?4，?4，?3，?R???1，1?，2?，4??2，1?，2?，4?，1?，2?，4?，3??

4. 解：∵每个集合的划分就可以确定一个等价关系

∴集合有多少个划分就可以确定多少个等价关系 4321C?C?C?C?15种。 4444

5. 解：

①R1UR2不是A上的等价关系

②R1?R2是A上的等价关系

③r?R1?R2? 是A上的等价关系

④R1oR2不是A上的等价关系

习题 5.6

2. 解：A??a,b,c?

2A???,?a?,?b?,?c?,?a,b?,?a,c?,?b,c?,?a,b,c??

?

C{b,c} <2,?>

6. 解：A??a,b,c,d?

17 3. 解：集合A上的空关系?、恒等关系IA都是等价关系和偏序关系。

2A???,?a?,?b?,?c?,?d?,?a,b?,?a,c?,?a,d?,?b,c?,?b,d?,?c,d?,?a,b,c?,?a,b,d?,?b,c,d?,?a,c,d?,?a,b,c,d?????a???b???c???d???a,b???a,c???a,d???b,c???b,d???c,d???a,b,c???a,b,d???a,c,d???b,c,d???a,b,c,d?

7. 证：i）自反性，对?b?B?A,

显然?b,b??B?B???b,b??R，（R的自反性） ?b,b??R?B?B

ii)反对称性，对?a,b?B,?a,b??R?B?B,?b,a??R?B?B

即?a,b??R,?b,a??R，由R的反对称性，?a?b

iii)传递性，对?a,b,c?B，设?a,b??R?B?B,?b,c??R?B?B，

则?a,b??R，?b,c??R。

由R的传递性，?a,c??R，显然?a,c??B?B

?

?a,c??R?B?B 18

习题6.2

4、证：

1）对?b1、b2?B，b1?b2

??a1、a2?A,?f(a1)?b1,f(a2)?b2 ?f(x)是满射，

由g(x)的定义，a1?g(b1),a2?g(b2)，且a1?g(b2),a2?g(b1)

a1?g(b2), a2?g(b1)，有 f(a1)?b2, f(a2)?b1 否则，如

与函数的定义相矛盾， ?g(1b)?g(2b), 即 g(x为单射)

2）而g(x)为单射时，对?b?B,并不能保证 g(b)??, ?f(x)不一定是满射

7、证： f:A?B,g:B?C

（1） 反证法：设不是单射， ?x1?x2?A,?f(x1)?f(x2) 即g?f(x1)?g(f(x1))?g(f(x2))?g?f(x2) 与g?f为单射矛盾（2）?g?f为满射 ?对?z?C, ?x?A, ?g?f(x)?g(f(x))?z 令f(x)?y?B ?? y?B, ?g(y)?z 即g为满射

习题6.4:

3．证明：非空有限集A与可数集B的笛卡尔积A×B也是可数集。 证明：设A={a1,a2,?,an｝

B={b1,b2,?,bn,?}

令Bi ={(ai,b1),(ai,b2),?,(ai,bn),?} (i≤n),则

19

A×B= , Bii?1k

因为B为可数集，所以Bi为可数集。A×B为有限个可数集的

并集。下面用归纳法证明有限个(m个)可数集的并集为可数集。 设Cm={cm1,cm2, ?,cmn, ?}

当m=2时，

构造双射f:N→C1∪C2,

N 1 2 3 4 5 6 ? n-1 n ? f(N) c11 c21 c12 c22 c13 c23 ? c1(n/2) c2(n/2) ?

所以2个可数集的并集为可数集。

假设m=k-1(k≥3)时结论成立，即k-1个可数集的并集为可数集，记为D。

则m=k时，可以构造类似的双射g:N→D∪Ck,所以为可数集。因而有

限个可数集的并集为可数集。所以A×B是可数集。

习题9.1

2C1．设G是一个(n,m)简单图。证明：m≤ ,n等号成立当且仅当G

是完全图.

证明：由欧拉定理，2m= ?d(k)，d(k)表示第k个结点的度

k?1n

因为G是简单图，所以d(k) ≤n-1,等号成立当且仅当G是完全图

d(k)?2m= ≤ , ?n?1n

k?1

k?1n

所以 2m≤n(n-1)

n(n?1)即 m≤2

2Cn20

3、解：（1）不是图的序列，因为奇数度结点的

个数不是偶数。

（2）、（3）、（4）都是图的序列。

4、证：

由欧拉定理， 2m??d(v)v?G?????d(v)???v?Gv?Gv?G?n???d(v)?2m?n?v?G2m?????n

9．若，称G是自补图。确定一个图为自补图的最低条件；画出一个自补图来。

解：设G=(n,m)，G’=(n,m’)

则m+m’=n(n-1)/2,所以m=m’=n(n-1)/4

4 4 v2

G

习题9.2 v2

1、若u和v是图中仅有的两个奇度数结点，证明u和v必是连通的。 证：（反证法）设v与u不连通

21

∴G={V1，V2} ，v与u分别属于V1，V2二个子图

∵ v与u是G中仅有的二个奇数度结点

∴v与u即是V1与V2中仅有的一个奇数度结点，与欧拉定理的 推论(9-1.1.1相矛盾,故v与u必连通

3、设(n,m)简单图G满足m＞(n-1)(n-2)/2，证明G必是连通图。构造一个m=(n-1)(n-2)/2的非连通简单图。

（书上证明更好）

5、设G=(V，E)是点度均为偶数的连通图。证明：对任何v∈V,ω(G-v)≤d(v)/2

证：（反证法）设结论不成立，即存在:v∈V,ω(G-v) ＞d(v)/2. 因为G是连通的，所以G-v的每个分支都至少有一个点与v相邻接，而且存在一个分支，其与v相邻接的点只有一条边与v相连（因为如每个分支中有二个以上的点与v相连，则

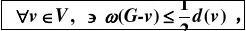
出现矛盾）

∴存在一个分支，其中只有一条边与v相连；因为G中每个结点的度数为偶数，所以在这个分支中就会出现一个奇度数结点，其余结点的度数全为偶数，与欧拉定理的推论相矛盾，故故对任何v∈V,ω(G-v)≤d(v)/2

9.证明：恰有两个非割点的简单连通图必是Pn(n≥2)

证明：归纳法。

n=2时，结论显然成立。

设n=k时结论成立，

22

当n=k+1时，设v1、vk是Pk上的两个非割点，vk+1是在Pk上增加的一个割点，如果结点vk+1不在Pk上的任意两个结点之间，则必与Pk上某两个结点构成一个回路，vk+1就不是割点，与只有两个非割点矛盾。故结论成立。

习题9.3

3、解： e12

v2

??v1 v2 v3 v4 v5 v6 v7?

?0 1 1 0 0 0 0?

??

?0 0 0 1 0 0 0?

A??0 0 0 1 1 0 0?

??

?1 0 1 0 1 0 0?

?0 0 0 0 0 0 0?

??

?0 0 0 0 1 0 1?

? 0 0 1 1 0?

?0 0??

??v1 v2 v3 v4 v5 v6 v7??

?1 1 1 1 1 0 0??v1 v2 v3 v4 v5 v6???1 1 1 1 0 0 ?1 1 1 1 1 0 0???1 1 1 1 0 0 P??1 1 1 1 1 0 0?

??

1 1 1 1 1P?PT??1 1 1 1 0 0

?

? 0 0?

?0 0 0 0 0 0 0??1 1 1 1 0 0 ???0 0 0 0 1 0 0 0 0 0 1 1 1??

????0 0 0 0 0 1 ?0 0 0 0 1 1 1????0 0 0 0 0 1

23 v7?0??0?0??0?0??1?1???

三个强分图

G({v1 ,v2 , v3 , v4})G({v5 })G({v6 ,v7 })?e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12???1 1 -1 0 0 0 0 0 0 0 0 0???-1 0 0 1 0 0 0 0 0 0 0 0???0 -1 0 0 1 -1 1 0 0 0 0 0?MG???0 0 1 -1 -1 1 0 1 0 0 0 0????0 0 0 0 0 0 -1 -1 -1 -1 0 0??0 0 0 0 0 0 0 0 1 0 -1 1?????0 0 0 0 0 0 0 0 0 1 1 -1??

5.证明：支数为k，阶数为n的无环图G，其关联矩阵的秩是n-k. 证明：将各支结点和边集中编号后，G的关联矩阵

?M1?0M???0??00M2000000??0???Mk?

由分块矩阵子公式及定理9-3.2，

γ(M)=γ(M1)+γ(M2)+?+γ(Mk)

=(n1-1)+(n2-1)+?+(nk-1)

=n-k

24

习题10.1

1、设一个树中度为k的结点数是nk，求它的叶的数目。 解：设L是叶的数目，m是树的边数,由Euler定理:

i

?k?2knk?L?2m

由树的定义:

m??i

k?2nk?L?1

??ikni

k?2k?L?2k??2nk?2L?2

?L??i

k?2(k?2)nk?2 (i?k?2)

习题10.2

6、证明正则二叉树必有奇数个结点。

证明：由正则二叉树的定义，其叶结点的个数必为偶数，设叶数为t，分支数为i。

由定理10-2.1： (m-1)i=t-1

∵ m=1 ∴ i=t-1 有分支点数是奇数

故结点数=i+t=奇数

习题10.4

3、证：（反证法）

设G=（n，m）和G’=（n，m’）都是平面图

25

由G的定义 m+m’=n(n-1)/2

由定理10-4.2 m≤3n-6 , m’≤3n-6

∴ m+m’=n(n-1)/2 ≤6n-12

有 n2-13n+24=(n-11)2+9n-97 ≤0

又∵（n-11)2 ≥0，n ≥11时,9n-97 ≥2

∴ （n-11)2 +9n-97 ≥2

与上式相矛盾， 故G与G’至少有一个是非平面图

4、证明：具有6个结点，12条边的简单连通平面图，它的面度都是3。

证：由Euler公式，n-m+f=2

∴ 6-12+f=2 f=8，即面数为8。

∵对每个面，其度数≥ 3

∴总面度≥3×8=24

∵总面度=2×m=24

∴每个面的度数为3

5、少于30条边的简单平面图至少有一个顶点的度不大于4。 证：（反证法）设所有顶点的度数5

由Euler公式，

由定理10-4.2 m≤3n-6

3n-6≥5n/2 即n≥12

则 m≥5n/2≥5×12/2=30 与 m＜30矛盾

因此，至少存在一个顶点的度数不超过4。

26

习题10.6

2、证明：4k+1阶的所有2k正则简单图都是哈密顿图。 证：∵ G是2k正则图，

∴ 对任意的u、v∈G，d(u)+d(v)=4k

由定理10-6-2 在G中存在一条Hamilton道路，设为： v1v2,?,v4k+1

1) v1v4k+1∈E， 则v1v2,?,v4k+1v1构成一个Hamilton圈 2) v1v4k+1 ?E， 则?vi1,vi2,?,vi2k与v1邻接

∵ G的阶数为4k+1

∴v4k?1必与vi1?1,vi2?1,?,vi2k?1中的一个点邻接， （否则d(v4k+1)=4k-1-2k=2k-1与d(v4k+1)=2k矛盾) 设vitv4k?1?E ，可构造v1,?vit?1,v4k?1v4k,?,vitv1 即为G的一个Hamilton圈，故G是一个Hamilton图

m?Cn?1?2证明G必是哈5、设G是(n,m)简单图，若 ,

密顿图。

证：（反证法）假设G不是哈密尔顿图，则 2

?s,t?G,?deg(s)?deg(t)?n

?2m??deg(v)??deg(v)?deg(s)?deg(t)v?Gv?G?{s,t} ?2m?v?G?{s,t}?deg(v)?n

因为G除结点s,t外的其余n-2结点之间最多可以构成完全 图，所以 2m<(n-2)(n-3)+n+n<n2-3n+6=(n-1)(n-2)+4 从而：

12m?(n?1)(n?2)?2?Cn?1?227 2

m?Cn?1?2矛盾，故结论成立。 与已知

习题11.1：

4.设<S，·>是一个含有幺元e的代数系统，a∈S.如果存在元b,c∈S使b·a=e(或a·c=e),则称b是a的左逆元(或c是a的右逆元)。证明：如果一个元既有左逆元b又有右逆元c，则必b=c.

证明：S上的运算·是可结合的。

b=b·e=b ·(a ·c)=(b ·a) ·c=e ·c=c

习题11.2

4、设半群<A,·>中任何两个不同元素关于运算“·”不可交换，证明：对任何a∈A,a·a=a

证明：（反证法）

设?a∈A,使得a ·a≠a,构造b= a ·a ，则

a·b= a ·a ·a =b ·a

即a、b 可交换，与已知条件相矛盾

∴ ? a∈A, a·a=a

5.设S={00,111,1010}是字符集Σ={0,1}上的字集合。试构造Σ*的一个包含集合S的最小的含幺子半群。

解：令空字符为λ.m,n,k为正整数，

T={λ,(00)m,(111)n,(1010)k} ∪{(00)m (111)n (1010)k}

∪{(00)m (1010)k(111)n} ∪{(111)n (00)m (1010)k} 28 2

∪{(111)n (1010)k(00)m} ∪{(1010)k(00)m (111)n}

∪{(1010)k (111)n(00)m}

习题11.3

1、证明：群中只有幺元是幂等元。

证：（反证法）

设?a?A,a

?1?e,?a?a，

22?1?1?a ?, ?a?a?a?a?a?e

?矛盾

5、写出s,?3中的全部子群。

解：?（1），（1 2）?，?（1），（1 3）?，?（1），（2 3）?， ?（1），（1 2 3），（1 3 2）?和二个平凡子群。

6、设<S，·>和<T，· >都是<G, · >的子群，令S∩T={x|x∈S∧S∈T},ST={s·t|s∈S∧t∈T}，证明：<{S∩T}, · >和<ST, · >也都是<G, · >的子群。

证明：1）∵ S、T是G的子群

∴ e?S , e?T 即 e?S ∩T

设 a，b?S ∩T，即a，b?S 和a，b?T

29

b-1 ?S 和b-1?T ∴ a?b-1 ?S 和a?b-1?T 即 a?b-1 ?S∩T ∴〈S∩T，?〉是G的子群

2） e?ST，设c、d?ST

则 ? a1?S，b1?T ，? c=a1b1，

? a2?S，b2?T ，? d=a2b2，

∵ d-1=b2-1a2-1

又 ∵S和T中的元素关于“?” 可交换

∴c?d-1= a1b1b2-1a2-1= a1a2-1b1b2-1 ?ST

即 ST是子群

习题11.4

1.阶数小于6的群必是交换群。

证明：

1阶群 是平凡的 , 显然是交换群.

2, 3和5都是素数, 由拉格朗日定理的推论2可知, 2阶、 3阶和5阶群 都是由一个元素生成的 , 它们都 是交换群 . (∵?ai,aj∈G,有ai·aj=ai+j=aj+i=aj·ai)

对于 4阶群 G, 若G中有4阶元素, 设为a, 则G=( a), G是交换群; 若 G 中无 4 阶元, 则由拉格朗日定理, G只可能含1阶元和2阶元. G也 是交换群

2、证明：设G是阶数大于1的群，

30

则 ? a≠e?G

构造G′={e,a}?G，

则 G′是G的交换群。

3.循环群的子群必是循环群

证明：设<G，·>是循环群，a是生成元，<H，·>是子群。

设H1={ai|i∈Z+,ai∈H}?H?G,记H1中所有元素ai的幂指数中

最小的是ar，则<H，·>=(ar)。这是因为，对?x∈H,x可表示成an(n∈Z+。设n=p·r+t(0≤t≤r-1)，假定t≠0,则有

at=an-pr=an·-pr=an·(ar)-p∈H

这与r 的最小性相矛盾，因此t=0，n=pr,x=an=(ar)p，所以<H，·>是以ar为生成元有循环群。

5、证明：

? 对 ? a?G , a?e 或 a3?e即 (a)?{e,a,a2} 或 (a)?{e} ? G??(a)a?G? G 的阶数n必是奇数

习题11.5:

4.证明下述结论：

(1)群中指数为2的子群是正规子群。

(2)两个正规子群S和T的交S∩T仍是正规子群。

证明：(1)设群G的子群H的指数为2，则H有两个左陪集H1、H2，

H1∩H2≠?，而且其中必有一个是H。假设H1=H，对

31

?a∈G，若aH=H,则Ha=H

?a∈G，若aH=H2,则Ha≠H，故Ha=H2

所以aH=Ha，即H是正规子群。

(2) ?a∈S∩T，对?x∈G，有xax-1∈S且xax-1∈T，即

xax-1∈S∩T，所以x(S∩T)x-1?S∩T.

习题11.7

7、证：1）对任何 a?R，∵ a*a=a

∴ (a+a)*a=a*a+a*a=a+a=a*(a+a)

∴ a+a=?

2）∵ (a*b)2=a*b=a2*b2

∴ 由定理11-4.1 ?R，*?为交换半群

故?R，+，*?为交换环

32