弦振动中误差的研究

实验目的：

（1）

（2） 研究弦振动中砝码的重力与绳子拉力之间的关系，测量砝码重力在多大范围内是和绳子张力相等的； 研究弦振动中频率的改变对绳子张力和密度的影响，算出它们的误

差。

实验原理：

如图（1）实验时在①和⑥间接上弦线（细铜丝），使弦线绕过定滑轮⑩结上砝码盘并接通正弦信号源。在磁场中，通有电流的弦线就会受到磁场力（称为安培力）的作用，若细铜丝上通有正弦交变电流时，则它在磁场中所受的与电流垂直的安培力，也随着正弦变化，移动两劈尖（铜块）即改变弦长，当固定弦长是

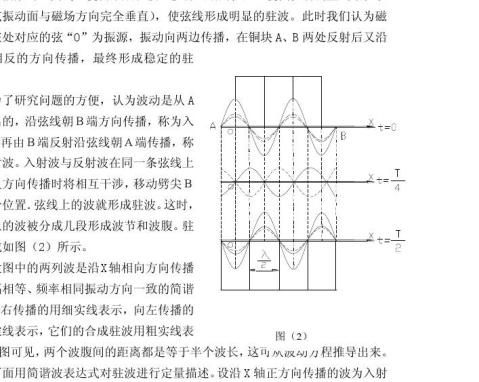
波。

波。示。波，沿X轴负方向传播的波为反射波，取它们振动位相始终相同的点作坐标原点 “O”，且在X＝0处，振动质点向上达最大位移时开始计时，则它们的波动方程分别为：

Y1＝Acos2?(ft－x/ ?)

Y2＝Acos[2? (ft＋x/λ)+ ?]

式中A为简谐波的振幅，f为频率，?为波长，X为弦线上质点的坐标位置。两波叠加后的合成波为驻波，其方程为：

Y1 ＋Y2＝2Acos[2?（x/ ?）+?/2]Acos2?ft ????? ①

由此可见，入射波与反射波合成后，弦上各点都在以同一频率作简谐振动，它们的振幅为｜2A cos[2?（x/ ?）+?/2] |，与时间无关t，只与质点的位置x有关。

由于波节处振幅为零，即：｜cos[2?（x/ ?）+?/2] |＝0

2?（x/ ?）+?/2＝(2k+1) ? / 2 ( k=0. 2. 3. ? )

可得波节的位置为：

x＝k? /2 ????? ②

而相邻两波节之间的距离为：

xk＋1－xk ＝(k＋1)?/2－k? / 2＝? / 2 ????? ③

又因为波腹处的质点振幅为最大，即 ｜cos[2?（x/ ?）+?/2] | =1

2?（x/ ?）+?/2 ＝k? ( k=0. 1. 2. 3. ? ?)

可得波腹的位置为：

x＝(2k-1)?/4 ????? ④

这样相邻的波腹间的距离也是半个波长。因此，在驻波实验中，只要测得相邻两波节或相邻两波腹间的距离，就能确定该波的波长。

在本实验中，由于固定弦的两端是由劈尖支撑的，故两端点称为波节，所以，只有当弦线的两个固定端之间的距离（弦长）等于半波长的整数倍时，才能形成驻波，这就是均匀弦振动产生驻波的条件，其数学表达式为：

L＝n? / 2 ( n=1. 2. 3. ? )

由此可得沿弦线传播的横波波长为：

?＝2L / n ????? ⑤

式中n为弦线上驻波的段数，即半波数。

根据波速、频率及波长的普遍关系式：V＝?f，将⑤式代入可得弦线上横波的传播速度：

V＝2Lf/n ????? ⑥

另一方面，根据波动理论，弦线上横波的传播速度为：

V＝(T/ρ)1/2 ????? ⑦

式中T为弦线中的张力，ρ为弦线单位长度的质量，即线密度。

再由⑥⑦式可得

f =（T/ρ）1/2（n/2L）

得 ?2l? FT??f?? ?n?22

由⑧式可知，当给定T、ρ、L，频率f只有满足以上公式关系，且积储相应能量时才能在弦线上有驻波形成。

实验步骤

1、

2、 连接实验装置。 测量弦线线密度?。测出弦线的质量及其长度。根据??，计算弦线密度。

3、

4、 测圆柱半径，用游标卡尺测量其直径，多次测量求平均值。 观测频率和绳子张力FT之间的关系

（1）取质50g的砝码挂于弦线的另一端，然后调节频率，调节劈尖的位置，得到稳定的驻波。分别测量波节N=1，N=2，N=3时，劈尖与圆柱底面圆心的距离。当频率大于130Hz时，取N=1，N=3，N=5.

（2）改变频率f从80Hz到150Hz,砝码质量不变，重复上述步骤（1），并记录数据。

5、 观测砝码质量mg与张力FT之间的关系

调节频率为100Hz，，砝码质量从10g到200g时调节劈尖的位置得到稳定的驻波，测量当N=1，N=2，N=3时，劈尖与圆柱底面圆心的距离。注：当砝码质量为15g时，取N=2，N=3，N=4.

6、 整理数据并处理

实验数据及处理

（一） 砝码质量对绳子张力和密度的影响：

1、?的测量

弦线 l?1cm

质量m?0.4g

-3

=0.4?10kg

?=m3

2、弦振动实验装置圆柱的半径

如下表:表中M为砝码的质量，N为波节数目，l为波节长度，为波长的平均值，?为绳子的密度，T为绳子拉力的平均值，

??100Hz 绳子密度??

F

?2?

2

绳子张力F???2?2

注：仅当M=15g时，波节数目为特殊情况。 其图像如下所示：（见下页）

（二）振动频率对绳子密度和张力的影响：

G?mg?50?10-3?9.8?0.49N

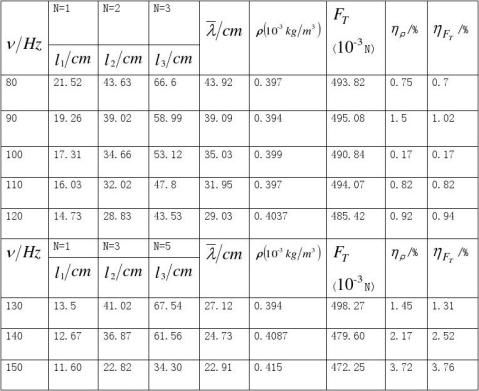
其图表如下图所示：

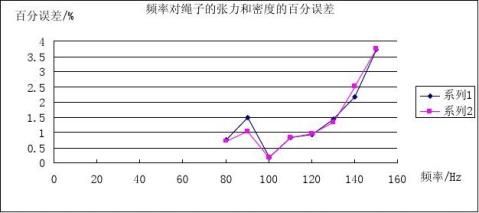
在实验过程中我们发现，

一方面，当固定振动的频率，改变砝码的质量。若砝码的质量过小，几乎是15g左右时，基本上无法研究，实验现象不明显，振动特别不稳定。但是，一旦砝码质量大于20g时，实验现象就明显了很多，而且绳子的张力与砝码的质量误差基本保持在2.5%以下，尤其是50g到100g之间时，误差基本保持在1%左右，可以说是非常小的。因此，我们在以后的实验过程中，只要砝码的质量大于40g往上，基本都是可取的。

另一方面，当固定砝码质量为50g时，我们通过改变频率来观测对绳子密度和拉力的影响。实验发现，70Hz以前的频率是基本上不能测试的，绳子的振动非常不稳定。因此，我们在实验过程中频率选在从80Hz到150Hz,由实验结论和实验图表可得：改变振动频率产生的实验误差是先减小到100Hz后又增大，因此在以后进行实验时，频率选在100Hz时，误差最小。

还有一个特殊现象，当频率过大，大于130Hz时，会出现一个特殊现象，当波节数目为偶数时，振动特别不稳定，劈尖到滑轮处也会出现微小的波节。而且，本来出现的两个波节会慢慢的合成一个波节，合成后的波节长度几乎和原来两个波节的长度相等，且振动幅度特别大，但是当出现奇数波节时，则不会出现这种情况，实验现象也相对稳定。这对实验带来了难度，因此，我们为了避免这种情况，减小实验误差，测量时，我们只选取奇数波节时的波节长度，这样，得出的结论就相当准确。

当然，由于实验室的实验仪器本身用于教学，不属于研究器材，因此，实验精度本身就不是很高，所以所测的实验数据也不是非常精确，导致实验出现误差，当然这个误差是无法避免的。

同时，在测量波节长度l时，用于人肉眼原因，测量的数据相对也会出现偏差。

实验心得

这次实验中，我们组成员分工明确，齐力配合，取得的成绩非常明显。实验过程中，由于实验数据的巨大性，我们走了不少弯路，经过小组成员讨论，查阅资料，然后以严谨的态度测量每一组实验数据，终于，功夫不负有心人。我们终

于得出了绳子拉力和砝码重力的关系，以及砝码的重力在什么情况下和绳子的张力近乎相等。同时，也研究了圆柱震动频率和绳子的张力及密度之间的关系，实验结论效果相当明显。

通过本次实验，我们体验到团队合作的重要性和必要性。没有队友的努力，根本不会有我们今天的成绩，当然，还有指导老师的指导，老师在我们都比较迷茫的时候给我们指了一条方向，实验才有了实质性的进展。在此，衷心感谢老师。

小组组长：於佩

组员：刘祥 王宝林

李佳 杨懿

2012-5-10

第二篇：弦振动时滞阻尼系统的稳定性分析及精确可控性研究

Ｐｈ．Ｍ．Ｄｉｓｓｅｒｔａｔｉｏｎ，ＺｈｅｎｇｚｈｏｕＵｎｉｖｅｒｓｉｔｙ，

Ｎｏ．２００９１２０１４０７０１０５０１８

ＴｈｅＳｔｕｄｙｏｆｔｈｅＳｔａｂｉｌｉｔｙＡｎａｌｙｓｉｓａｎｄＥｘａｃｔＣｏｎｔｒｏｌｌａｂｉｌｉｔｙｏｆ

ｔｈｅＳｔｒｉｎｇＤａｍｐｅｄＳｙｓｔｅｍｂｙＴｉｍｅＤｅｌａｙＣａｎｄｉｄａｔｅ：ＸｉｎＹａｎｇ

Ｓｕｐｅｒｖｉｓｏｒ：ＰｒｏｆｅｓｓｏｒＪｕｎｇｕｏＪｉａＳｐｅｃｉａｌｉｔｙ：ＯｐｅｒａｔｉｏｎａｌＲｅｓｅａｒｃｈａｎｄＣｙｂｅｒｎｅｔｉｃｓＤｅｐａｒｔｍｅｎｔｏｆＭａｔｈｅｍａｔｉｃｓ，ＺｈｅｎｇｚｈｏｕＵｎｉｖｅｒｓｉｔｙ

Ｚｈｅｎｇｚｈｏｕ，４５０００１，Ｐ．Ｒ．Ｃｈｉｎａ

Ａｐｒｉｌ，２０１２

本人郑重声明：所里交的学位论

成果。除文中已经注明引用的内容外，

过的科研成果。对本文的研究作出重要贡献的个人和集体，均已在文中以明确方式标明。本声明的法律责任由本人承担。

学位论文作者：日期：谢埠朋多９日

学位论文使用授权声明

本人在导师指导下完成的论文及相关的职务作品，知识产权归属郑州大学。根据郑州大学有关保留、使用学位论文的规定，同意学校保留或向国家有关部门或机构送交论文的复印件和电子版，允许论文被查阅和借阅；本人授权郑州大学可以将本学位论文的全部或部分编入有关数据库进行检索，可以采用影印、缩印或者其他复制手段保存论文和汇编本学位论文。本人离校后发表、使用学位论文或与该学位论文直接相关的学术论文或成果时，第一署名单位仍然为郑州大学。保密论文在解密后应遵守此规定。

学位论文作者：日期沙ｆ埠肋；妇

摘要

本文从含阻尼具有边界时滞输入的弦系统控制问题

方程化为无阻尼的情况．证明了系统的算子生成了一个

Ｒｉｅｓｚ基谱方法证明了系统Ｐｄｅｓｚ基的存在性．最后讨论了系统的精确可控性问题．关键词：弦系统；时滞边界控制；Ｇ半群；Ｒｉｅｓｚ基；指数稳定性；可控性．

Ａｂｓｔｒａｃｔ

Ｉｎｔｈｉｓｐａｐｅｒ，ｓｔａｒｔｉｎｇｗｉｔｈｓｏｍｅｐｒｏｂｌｅｍｏｆｓｔｒｉｎｇｓｙｓｔｅｍｗｉｔｈｄａｍｐｉｎｇａｎｄｂｏｕｎｄａｒｙｔｉｍｅ－ｄｅｌａｙｉｎｐｕｔ，ｔｈｅｓｔｒｉｎｇｓｙｓｔｅｍｗｉｔｈｌｉｎｅａｒｄａｍｐｉｎｇｉｓｔｕｒｎｅｄｉｎｔｏａｕｎｄａｍｐｅｄｔｈｒｏｕｇｈａｔｒａｎｓｆｏｒｍ．Ｗｅ

ａｏｂｔａｉｎｔｈａｔｔｈｅｓｙｓｔｅｍｏｐｅｒａｔｏｒｇｅｎｅｒａｔｅｓａＣｏ—ｓｅｍｉｇｒｏｕｐａｎｄｔｈｅｓｙｓｔｅｍｉｓＲｉｅｓｚｏｎｅ，ｗｉｔｈｔｈｅｐｒｏｃｅｄｕｒｅｓｏｆｓｐｅｃｔｒａｌａｎａｌｙｓｉｓａｎｄＲｉｅｓｚｂａｓｅｓｍｅｔｈｏｄ

ｉｓｄｉｓｃｕｓｓｅｄ．ｏｆｓｉｎｅｔｙｐｅｄｆｕｎｃｔｉｏｎｓ．Ｆｉｎａｌｌｙ，ｔｈｅｅｘａｃｔｃｏｎｔｒｏｌｌａｂｉｌｉｔｙｐｒｏｂｌｅｍｏｆｔｈｅｓｙｓｔｅｍ

ＫｅｙＷｏｒｄｓ：ＳｔｒｉｎｇＳｙｓｔｅｍ；Ｔｉｍｅ－ｄｅｌａｙＢｏｕｎｄａｒｙＣｏｎｔｒｏｌ；Ｃｏ—Ｓｅｍｉｇｒｏｕｐ；ＲｉｅｓｚＢａｓｉｅｓ；

Ｓｔａｂｉｌｉｔｙ；Ｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ．Ｅｘｐｏｎｅｎｔｉａｌ

目录

第一章引言…………………………………………………………１

第二章弦振动时滞阻尼系统算子生成岛半群…………………………１０

第三章弦振动时滞阻尼系统的稳定性分析……………………………．．２１

第四章弦振动时滞阻尼系统的可控性…………………………………２６参考文献……………………………………………………………．．３ｌ致谤｝…………………………………………………………………．３４

第一章引言

本章主要是介绍弦振动时滞阻尼系统的稳定性分析和精确可控性的研究背景、现状及意义，并给出了本文的主要研究工作和内容的大致安排，最后介绍本文所需要的有关预备知识．

１．１弦振动时滞阻尼系统的研究背景和现状

●

＾

弦振动方程亦称一维波动方程，状态方程是一类双曲型偏微分方程．弦振动边界反馈控制问题（亦简称弦系统）属于双曲型偏微分方程的一类数学物理边值问题，它是分布参数弹性控制系统的一个主要分支或典型分支．众所周知，双曲型方程是偏微分方程理论中研究的相对比较不完善的一种，从而对于弦系统的研究不仅有较好的使用价值，而且还具有较高的理论价值１１】（贾军国，２００６）．

由于具有边界控制或局部边界控制的分布参数系统的控制易于实现，适用范围广泛，已越来越引起人们的关注．作为边界控制的一个典型特例，弦系统问题的研究从上世纪７０年代末，时至今日，一直是系统控制与偏微分方程数学理论两个领域的一个关注焦点Ｎ－１４１．

鉴于在实际工程中的自动控制中，对任何反馈控制的实现，阻尼与时滞总是不能避免的，因而无论是研究阻尼、时滞对反馈闭、开环系统的单独影响，还是研究阻尼、时滞对反馈控制系统的复合影响都是重要的主流工作【ｌ】１．

在系统反馈机制的工程实践中，系统中时滞的出现是不可避免的，也是不可忽略的，所以说处理好时滞所带来的问题是十分关键的，尤其是在要求非常精密的设计不同零件之间的信息传输方面．在现实生活中，时滞现象是普遍的，无论是在工程方面，还是自然界中的生物生长环境中，时滞都经常出现的．但是对于某些特定的系统来说，时滞所带来的影响可能很大，也可能很小．其对于系统的稳定性也是如此，有的时候，哪怕很微小的时滞都足以破坏整个系统的稳定性，有的时候时滞可能就不会起太大的作用．在文１５１（Ｉ．ＧｕｍｏｗｓｋｉａｎｄＣ．Ｍｉｔａ，１９６８）中提供了一个典型的例子，它揭示了对于一个微分方程系统，时滞的出现破坏了系统的稳定性，而且还引起了系统解的中期震荡．

当然，对于一个系统来说，时滞的出现并不是总是带来负面的影响，有时候，合适的时１

。，滞反而会改善系统的性能，如Ｓｕｈ和Ｂｉｅｎ对最优控制器加上时滞，使新得到的控制器对于噪声扰动的感应方面具有了优良的性能１８］．关于波动方程零边界问题的研究已经有了较好的发展，而本文主要研究的是相对比较单纯的一维有限区间上的时滞边界反馈控制系统问题，这一类问题的特点是方程比较简单，但是边界比较复杂，具有各种反馈控制．文中讨论了系统算子生成一个岛半群，简单分析了该半群的谱分布，并采用Ｒｉｅｓｚ基的方法得到了该系统的稳定性．对于弦振动边界反馈系统，首先给小这样一类具有粘性阻尼项的弦振动边界反馈系统：ｌｕｕ—ｔ上船＋２ａｕｔ＋ａ２ｕ＝０，ｚ∈（０，１），ｔ∈（０，ｏｏ），｛乱（ｏ，ｔ）＝ｏ，ｕ２（１，ｔ）＝，（￡），ｔ＞０，（１．１）Ｉｕ（ｚ，０）＝咖（ｚ），地（ｚ，０）＝ｔ】ｂ（ｚ），ｚ∈１０，ｌ】．其中ｆ（ｔ）＝－ｋｕｔ（１，ｚ）是系统的边界输入控制，ｔ‘＝ｕ（ｘ，ｔ）表示定义在１０，１】×【０，∞）上的粘弹性弦振动质点在弦上位于位置ｚ，时刻￡的垂直位移，物理参数口，ｋ∈（０，ｏｏ）均为正数，分别表示系统的粘性阻尼系数、控制反馈系数．如，铷是两个已知的初始函数．对于

系统（１．１）的稳定性研究，贾军国教授对该阻尼系统用泛函分析算子理论进行了讨论ｌｌ】’１７１－１８】，通过分析或估计系统算子的谱及上界，利用谱定增长条件定理得到系统能量指数衰减率与系统阻尼及边界反馈之间的关系，有了很好的结论：当按能量积分法或频域分析法得到系统的指数稳定性时，系统半群的谱定增长条件必成立，从而系统能量的指数衰减速率即为系统算子的谱上界．从上述系统出发，在系统中加入延迟因子丁，即当系统的观察或控制输入时所出现的时间延迟，也就是说，系统ｔ时刻接受到的是￡一下刻的观测值，即

ｆＣｔ）＝一克毗（１，ｔ一７．），７．＞０

则相应的闭环系统化为

Ｉｕｕ—ｔ正船＋２ａｕｔ＋口２ｔ上＝０，。∈（０，１），￡∈（０，ｏｏ），

｛以０＇Ｄ＿０，ｂ０，

（１．２）

ｌ地（１，ｔ）＝－ｋｕｔ（１，ｔ—ｒ），ｔ＞７－，

Ｉ让（ｚ，０）＝知（ｚ），地（ｚ，０）＝Ｖｏ（Ｘ）￥∈ｆ０，１１．

其中，在【－－Ｔ，０】时间段上，ｆ（ｔ）＝垆（￡），且妒（￡）∈Ｌ２［－－Ｔ，０】为给定的已知函数．对于此系统文【１】也给出了一些讨论，主要是讨论了闭环系统（１．２）的系统算子的谱分析．通过将系统２

化为抽象的Ｃａｕｃｈｙ问题，得到系统算子的谱特征方程，且给出了算子的特征值的位置分布，并分析了时滞控制输入系统与非时滞系统特征值位置变化的内在原因．但对于系统的稳定性只进行了框架分析，没有作进一步的研究．

１．２本文所要研究的重要内容及工作安排

本文从系统（１．２）出发，将内容作如下安排：

第一章是所要研究问题的有关背景、现状和意义，以及所要研究的内容，必要的预备知识．

第二章、第三章是基于系统（１．２），通过线性变换将方程化为抽象的柯（Ｃａｕｃｈｙ）Ｉｈ］题，从而系统算子生成岛半群，通过证明系统Ｒｉｓｚｅ基的存在性，研究半群的指数稳定性．

第四章是简单的研究一下在有限的时间内系统的精确可控性．

１．３预备知识

１．３．１有界线性算子半群的基本理论

本文主要是利用线性算子半群的理论讨论系统的稳定性以及相关的其它问题，故而半群方面的理论是必不可少的．

定）Ｚ１．３．１１９１设ｘ是Ｂａｎａｃｈ空间，Ｔ：ｆ０，Ｏ（３】一ｃ（ｘ）是算子值函数，如果满足：（ｉ）Ｔ（０）＝，（恒等算子）；

（ｆｉ）Ｔ（ｔ）Ｔ（ｓ）＝Ｔ（ｔ＋ｓ），Ｖｔ，ｓ≥０，

则称Ｔ（￡）（￡≥０）为Ｘ上的有界线性算子半群，简称为算子半群或半群．

定义１．３．２１９］设Ｔ（￡）（￡≥０）是空间ｘ上的算子半群，如果ｚ∈Ｘ使得Ｔ（ｔ）ｘ在￡＝０处强可导，即极限

ｔ—’ｏ＋ｔｌｉｍ．Ｔ．．．．．（．．．ｔ．．）．．．ｘ．．．．．－．．．．．．—ｘ—（１．３）

在Ｘ中存在，其极限记为Ａｘ，则算子以称为半群Ｔ（ｔ）的无穷小生成元，简称为生成元．

Ｕ３

使得极限（１．３）存在的空间Ｘ中元素ｚ的全体称为算子Ａ的定义域，记为Ｄ（Ａ）．

定义１．３．３Ｐ］若算子半群Ｔ（￡）（￡≥０）作为算子函数在ｔ≥０上一致（强、弱）连续，则称Ｔ（Ｏ（ｔ≥０）是一致（强、弱）连续半群．强连续半群又称为岛半群．

定理１．３．１Ｐ］设Ｔ（￡）（￡≥ｏ）是以线性算子Ａ为生成元的Ｂａｎａｃｈ空间上的岛半群，其指标为蛐，则当ＲｅＡ＞蛐时，入∈，，（Ａ），并且算子Ａ在Ａ处的预解式可表示为

，∞

Ｒ（入；Ａ）＝／ｅ以。Ｔ（ｔ）ｚｄｘ．（１．４）

ＪＯ

定理１．３．２１１０】（Ｈｉｌｌｅ－Ｙｏｓｉｄａ）线性算子Ａ为某岛半群Ｔ（￡）（￡≥０）生成元的充分必要条件：

（１）Ａ是闭稠定线性算子；

（２）存在实数ｕ，使得Ａ的预解集ｐ（Ａ））｛Ａ＝ｚ＋们∈Ｃｌｘ∈∞，ｏ。））；

（３）存在常数Ｍ＞０，使当ｚ＝ＲｅＡ＞ｕ时，有

（１．５）

由Ｈｉｌｌｅ－Ｙｏｓｉｄａ定理我们可以看出，岛半群Ｔ（ｔ）与其生成元Ａ之间具有非常明显的依赖关系．Ｈｉｌｌｅ－Ｙｏｓｉｄａ是线性算子半群理论中的重要定理之一，表述了能生成岛半群的线性算子Ａ的特征．

定义１．３．４１１０】设Ｘ是一个Ｂ龃ａｃｈ空间，Ｘ’是其对偶空间，以＜ｚ，矿＞表示矿∈Ｘ?在ｚ∈Ｘ处的值，则定义ｚ的对偶集Ｆ（ｘ）为：

Ｆ（ｘ）圭｛ｚ‘Ｉｚ‘∈Ｘ’，且＜ｚ，ｚ’＞－－ｌＩｘｌｌ２＝ＩＩｘ‘０２）．

而线性算子Ａ称为耗散的：如果对于每一个ｚ∈Ｄ（Ａ），存在矿∈Ｆ＠），使得下式

Ｒｅ（Ａｘ，矿）≤０

成立．

定理１．３．３１１０】（Ｌｕｍｅｒ－Ｐｈｉｌｌｉｐｓ）设Ａ是Ｘ中具有稠定义域的线性算子，若Ａ耗散的，且存在Ａｏ使得Ａｏｌ—Ａ的值域Ｒ（Ａｏ，一Ａ）是ｘ，则Ａ是一个Ｘ上岛收缩的有界线性算子半群的无穷小生成元．４

注：易得到，若Ａ是一闭稠定线性算子，且Ａ，以‘（以‘是Ａ的伴随算子）均为耗散的，则Ａ是Ｘ上一个岛收缩的有界算子半群的无穷小生成元．特别，当ｘ是Ｈｉｌｂｅｒｔ空间时，Ａ的耗散性可以通过内积＜，＞形式表示，即：若对任意的ｚ∈Ｘ有Ｒｅ（Ａｘ，ｚ）≤０，则Ａ是耗散的１１１１．

１．３．２算子的谱及其生成半群的谱定增长条件

线性算子的谱Ｉｌ２】－１１４】

设Ｘ为复Ｂａｎａｃｈ空间，Ａ为Ｄ（Ａ）ｃＸ到自身的（无界）线性算子，则按通常定义可得Ａ的谱点集有分类：口（Ａ）＝ａｐ（Ａ）Ｕｃｒｃ（Ａ）Ｕ西（Ａ）．

其中ａｐ（Ａ），ｃｒｃ∽），ａｒｒ（Ａ）分别表示Ａ的本征值（点谱）集，连续谱点集及剩余谱点集．而Ａ的正则点集：

ｐ（Ａ）圭｛Ａ∈ＣＩＭ—Ａ可逆，其值域Ｒ（Ｍ—Ａ）在ｘ中稠密，且（入，一Ａ）．１有界）＝ｃＶ（Ａ）．当Ａ∈唧（以），称ｄｉｍ｛ｘ∈ｘｌ（Ａ，一以净＝口）为本征值Ａ的（几何）重数．

注：无界线性算子的谱集与有界线性算子是不同的，其谱集有可能是整个复平面，也有可能是空集．

在偏微分方程的应用中，一般均设Ａ是闭的，即Ａ的图像Ｇ（Ａ）圭｛（ｚ，Ａｘ）ｌｘ∈Ｄ（Ａ）ｃｘ）在乘积赋范空间Ｘ×Ｘ中是闭集．有闭线性算子定义及闭图像定理可知：闭线性算子是有界线性算子的一种推广，他是作为无界线性算子失去有界性（连续性）的一种补偿．显然，无界闭稠定线性算子，其定义域一定非闭．则Ａ的正则点集：

ｐ（Ａ）＝｛Ａ∈ＣＩＡ，一／ｔ可逆，其值域Ｒ（Ａ，一Ａ）＝ｘ）；

另外，当０∈ｐ（Ａ），则Ａ必为闭算子．

近似点谱概念：称复数Ａ为Ａ的近似点谱，如果存在ｘ中的一个点列｛ｚｎ），满足：

０ｚｎ０＝１，且０（Ａ，一月）ｚｎ０—０（ｎ—ｏｏ）．

全体近似点谱记作ｃｒｏ（Ａ）．

注：近似点谱也为谱点，且有性质：

（１）唧（Ａ）Ｕ口。（／Ｉ）ｃ乳（Ａ）．５

（２）若％（Ａ）＝１２ｊ，那么ａａ（Ａ）＝盯（／Ｉ）．

（３）ａ（Ａ）的边界点必为近似谱点．

本质谱概念：在算子Ａ的谱集ａ（Ａ）中，ａ（Ａ）的全体聚点和无穷维的孤立本征值统称为Ａ的本质谱（Ｅｓｓｅｎｔｉａｌｓｐｅｃｔｒｕｍ），记为吼（Ａ）．本质谱在谱集ａ（Ａ）中的补集称为Ａ的离散谱（Ｄｉｓｃｒｅｔｅｓｐｅｃｔｒｕｍ），记为ａｄ（Ａ），即有ａｄ（Ａ）＝仃（／ｔ）＼几（Ａ）．如果仃。（／Ｉ）＝Ｄ，则称Ａ的谱是离散的．

注：昀（／Ｉ）是以的有限孤立本征值全体所组成的集合，而当ｘ为Ｈｉｌｂｅｒｔ空间，Ａ为（无界）自伴算子，则Ａ的本质谱在紧自伴扰动下保持不变，即当算子Ｂ为紧自伴算子时，Ａ＋Ｂ亦为自伴的，且有吼（Ａ＋Ｂ）＝ａｒｅ（Ａ）．

离散算子概念：当算子Ａ具有预解紧，即存在入∈ＪＤ（Ａ），使Ｒ（入，Ａ）圭（ｈｉ—Ａ）一１为Ｘ上的紧线性算子，则可以推出Ａ的谱是离散的，此时我们称Ａ是离散算子．离散算子是波动方程边值问题中经常出现的系统算子．

本征值谱点的重数

几何重数、代数重数概念：设以为Ｂａｎａｃｈ空间ｘ上Ｄ（Ａ）＿Ｘ的闭线性算子，Ａ∈ａｐ（Ａ），称入的维数：ｄｉｍ｛ｘ∈Ｘｌ（入Ｉ—Ａ）ｘ＝ｏ）＝ｄｉｍＫｅｒ（ＡＩ—Ａ）为Ａ的几何重数，记作ｍ９（入），而对ｚ∈Ｋｅｒ（ＡＩ—Ａ）的ｚ，称为对应Ａ的本证元（向量）；若ｚ∈Ｄ（Ａ）且存在正整数Ｚ≥ｌ，使得ｚ∈Ｋｅｒ（Ａｌ—Ａ）‘，则称ｚ为对应Ａ的广义本证元（向量），而正整数ｍｏ（Ａ）圭ｄｉｍ｛ｘＩ｜ｚ∈Ⅳ，使得（入，一以）‘ｚ＝０）称为Ａ的代数重数．

注：仇口（Ａ）≥％（Ａ）．若存在正整数ｆｏ，使得Ｋｅｒ（ＡＩ—Ａ）ｃ…ＣＫｅｒ（ＡＩ—Ａ）ｂ＝Ｋｅｒ（Ａｌ—Ａ）ｂ＋１，则称ｌｏ为入的指标（ｉｎｄｅｘ），记作ｉｎｄ（Ａ）；故‰（入）＝ｍ口（入），当且仅当入的指标ｉｎｄ（Ａ）＝ｌｏ＝１．

若存在全纯函数，（ｚ），使得，（Ａ）＝…＝，（扣１）（入）＝０，ｆｋ（入）≠０，则称正整数ｋ为本征值入关于，的消失阶（ｖａｎｉｓｈｉｎｇｏｒｄｅｒ）（ｋ亦称为入作为，的零点的零点阶数），记作ｖ８ｎ，（Ａ）．

定义１．３．５称全纯函数，（ｚ）是指数型的，如果存在常数Ｍ＞０，Ｑ∈Ｒ使得

Ｉ，（２）Ｉ≤Ｍｅａ｜ｚＩ’比∈Ｃ

成立；而指数型函数，（ｚ）称为是正弦型的，是指，（ｚ）满足下面两个条件：６

（１）．，（ｚ）的零点均位于带域｛ｚ∈ＣｌＩＰ呛ｚＩ?≤Ｃ，其中Ｃ＞ｏ）；

（２）．存在正常数Ｃｌ，ｃ２，及；ＺＯ∈Ｒ使得对任意Ｙ∈Ｒ，有ｃ１≤Ｉｆ（ｘｏ＋ｉｖ）Ｉ≤ｃ２．

定理１．３．４设ｆ（ｚ）为正弦型全纯函数，则ｆ（ｚ）的全体零点（若零点出现重复按零点阶或消失阶重复计算）是有限个可分离集的并，即存在正整数ｍ，使得

，的零点集２ｋＵ＝ｌ＆，‘彩Ａ（的ｉｎ，如ｆ（的∈鼠Ｉ九（七）一～（尼）Ｉ＞。

因此，正弦型函数的所有零点的零点阶或消失阶是一致有界的．

注１【１５】：若存在ｕ∈冗，使得ｅ－ｒ（ｚ）为正弦型函数，ｒ（ｚ）＝０是算子Ａ的谱特征方程，即Ａ作为Ａ的本征值的充要条件是Ａ为ｒ（ｚ）的零点，则入作为Ａ的本征值的代数重数等于入作为ｒ（ｚ）的零点阶数，即ｍ口Ｑ）＝ｖ锄ｒ（入）．

注２【１０１：在Ｈｉｌｂｅｒｔ空间中，若Ａ为自伴离散算子或反自伴离散算子，则Ａ的本征值的几何重数和代数重数相等，且其本征函数集构成Ｈｉｌｂｅｒｔ空间的一组规范正交基．（Ａ反自伴，是指Ａ‘＝一Ａ，从而月的谱均位于虚轴上．）

系统的谱确定增长假设【１７】

设Ａ是Ｂａｎａｃｈ空间上的一强连续有界线性算子半群Ｔ（ｔ）的生成算子，记

舭）圭｛ｓｕｐ恤刈爬州川ｈ勃∽）≠玖．（１．６）

Ｉ—ｏｏ，若ｏ－（Ａ）＝历．

且

ｕ（Ａ）圭ｉｎｆ｛半掣：ｔ＞ｏ），（１．７）

并约定ｌｎＯ＝－－００，我们分别称ｓ（Ａ），ｕ（Ａ）为算子Ａ的谱（上）界和由Ａ生成的半群Ｔ（ｔ）的增长阶，并将这两个常数相等的情形，即

８（Ａ）＝ｕ（Ａ）（１．８）

叫作系统的谱确定增长假设（条件）．由岛半群的性质，不难得出

ｕ（Ａ）＝ｉｎｆ｛ｗ∈ＲＩ３Ｍ．≥１，使得ＩＩ丁（￡）０≤朋乙ｅ埘，Ｖｔ≥ｏ）．（１．９）７

注意：ｗ（Ａ）本质上刻画了半群Ｔ（ｔ）的增长速度，从ｕ（以）的定义上可知，当ｕ＞ｗ（Ａ）时，存在常数Ｍ≥１使得

ＩＩＴ（０１Ｉ≤Ｍｅ讲，耽≥０

从而半群Ｔ（ｔ）的指数稳定性取决于条件ｕ（Ａ）＜０．因此，当（１．８）成立时，只要（１．６）中的ｓ（Ａ）＜０，则线性系统

未ｚ（￡）＝ＡｘＣｔ），ｚ（ｏ）＝ｚ。

就是指数稳定的．于是，在系统的谱确定增长假设（１．８）成立的条件下，半群Ｔ（ｔ）的指数稳定性完全由Ａ的谱决定，这就是称（１．８）为系统的谱确定增长假设的原因．

本质谱与增长阶的概念及相关结论：

概念：设Ｔ为Ｂａｎａｃｈ空间Ｘ上的有界线性算子，则定义Ｔ的本质谱半径为：％（Ｔ）圭ｉｎｆ｛ｒ＞０Ｉ入∈仃（丁），当…≥７．，则入必为Ｔ的孤立的有限维本征值）．若Ｔ（ｔ）为算子Ａ生成的Ｃｏ半群，则Ｔ（ｔ）的本质增长阶ｗｅ（Ａ）为

州）圭坐掣渺。

结论：算子的本质谱半径及半群的本质增长阶的两个重要性质：

（１）．对任意紧算子Ｋ，有ｒｅ（Ｔ＋Ｋ）＝ｒｅ（Ｔ），即本质谱半径在紧算子扰动下不变．（２）．ｗ（Ａ）＝ｍａｘ｛ｓ（Ａ），魄（Ａ）＞，这里ｓ（Ａ），ｗＣＡ）为算子Ａ的谱（上）界和由Ａ生成的半群Ｔ（ｔ）的增长阶．

有上述性质（２）我们可以得出：若算子Ａ满足条件：ｓＣＡ）≥此（／１），特别是当Ａ生成一紧岛半群Ｔ（Ｏ，则由ｒｃ（丁（￡））＝０，可得忱＝一ｏｏ，从而ｓＣＡ）＝ｕ（Ａ），即Ａ一定满足谱确定增长假设．

系统指数稳定性的判断依据

定理１．３．５１１８】设Ｔ（ｔ）是Ｈｉｌｂｅｒｔ空间日上闭稠定线性算子Ａ生成的半群．则有结论：半群Ｔ（ｔ）指数稳定当且仅当对某个Ｐ≥１，Ｔ（ｔ）是弱胆稳定的，即

，∞

／Ｉ＜Ｔ（ｔ）ｘ，Ｙ＞ｌｐｄｔ＜＋ｏｏ．

．，０

进一步可得：半群Ｔ（ｔ）是指数稳定的当且仅当８

（１）．｛Ａ∈ＣＩＰｅＡ≥０｝ｃｐ（Ａ）；

（２）．ｓｕｐ｛ｌＩＲ（ａ＋ｉｔ；Ａ）ｌｌｌ＇＂∈Ｒ）＜００，Ｖａ＞０．

此外，若Ｔ（ｔ）是一致有界的，即存在正常数Ｍ，使得对Ｖｔ≥０，有ＩＩＴ（ｔ）ｔＩ≤Ｍ，则条件（２）可以化为更简单的形式：

（３）．ｓｕｐ｛ｌｌＲ（ｉｒ；Ａ）ｌｌｌ７－∈Ｒ）＜ＯＯ．９

第二章弦振动时滞阻尼系统算子生成岛半群

本章节为了更好的讨论系统（１．２）主要是通过一线性变换将原来具有阻尼项的系统化为无阻尼的系统．进一步，为了方便讨论时滞的问题，我们通过变换将无阻尼的系统方程转化为一个方程组，随之通过讨论证明了系统生成一个岛半群，并简单的讨论了系统的算子的谱的特点．

２．１问题的提出及其方程的变换

我们考虑的模型是下面一维具有时滞粘性阻尼项的弦振动方程，方程如下：

ｌ锄一弘犯＋２ａｕｔ＋ａ２ｔ上＝０，ｚ∈（０，１），ｔ∈（０，∞），

｛“０’幻＿０，ｂ０＇

（２．１）

Ｉｕ霉（１，￡）＝－ｋｕｔ（１，ｔ一下），ｔ＞Ｌ

Ｉ扎（ｚ，０）＝伽（ｚ），地（ｚ，０）＝如（ｚ）童∈【０，１】．

其中，牡＝ｕ（ｘ，ｔ）表示定义在【０，１】×【０，ＯＯ）上的粘弹性弦振动质点在弦上位于位置ｚ，时刻ｔ的垂直位移，，＞０表示时滞量的大小，物理参数ａ，ｋ∈（０，∞）均为正数，分别表示系统的粘性阻尼系数、控制反馈系数．Ｕｏ，铷是两个已知的初始函数．

鉴于此方程是有阻尼的情况，为了能够更好的讨论系统（２．１），我们可以通过一个变换，即通过变换：ｗ（ｘ，ｔ）＝ｅａｔＵ（Ｘ，￡），将系统（２．１）化为一种无阻尼的情形，即仅具有时滞的反馈控制系统：

叫托一魄２＝０，Ｚ∈０＾１Ｘ￡＞０

ｗ（Ｏ，ｔ）＝０，ｔ＞，

忱（１，ｔ）＝－ｋｅａ下（叫ｔ（１，ｔ一丁）一ａｗ（１，ｔ一７－）），ｔ＞，

，Ｉ、２２

饥（１，ｐ）＝≯（口），ｗｔ（１，口）＝妒（口），ｐ∈一ｔ．，，

加（ｚ，０）＝ｗｏ（ｔ）＝ｔ幻０），Ｚ∈Ｏｄ１

ｗｔ（ｘ，０）＝Ｗｌ（Ｘ）＝Ⅶ（ｚ）＋口呦（ｚ），Ｚ∈＠吼Ｌ卜０∞∞＾ｌ叫）¨

其中咖（口），妒（口）∈Ｌ２［－－７＂，０】均表示某一给定的平方可积函数．进一步，为了更方便的处理时滞ｒ，以便将方程（２．２）化为抽象的柯西（Ｃａｕｃｈｙ）问题，对其位移函数及其导数做

１０

如下变换：

ｐ（ｘ，ｔ）＝叫ｚ（ｚ，ｔ）＋ｗｔ（ｘ，￡），。∈（０，１），ｑ（ｘ，ｚ）＝ｗｘ（ｘ，￡）一ｗｔ（ｘ，ｔ），ｚ∈（０，１），，７（ｚ，ｔ）＝魄（１，ｔ—ｒｘ）‘＋ｗｔ（１，ｔ—ｒｘ），ｚ∈（０，１），ｒ（ｘ，ｔ）＝叫ｚ（１，￡一ｒｚ）一ｗｔ（１，ｔ—ｒｘ），ｚ∈（０，１），ｓ＠，ｔ）＝蚍＠，ｔ—ｒ）＋ｗｔ（ｘ，亡一７．），ｚ∈（０，１），ｙ（ｘ，ｔ）＝％（ｚ，￡一ｒ）一ｗｔ（ｘ，ｔ—下），２∈（０，１）．

因此，方程（２．２）中的第一行我们就可以化为：

爰（：墨：：）＝１Ｉ－。１）－蕊ａｚ（ｐｑ（（ｘｚ’，ｔ幻））

原方程的边界条件可化为相应的边界条件：

（０￡）＝ｑ（０，￡），ｓ（０）＝ｙ（ｏ）ｔ＞０（１￡）＋口（１，ｚ）＝

一ｎ片（ｓ（ｚ，￡）＋ｙ（ｘ，￡）血）】，一七ｅ：‘ｔ７（１，２）一，．（１，２）２＞ｏ

（０￡）＝ｐ（１，￡），，．（０）＝ｑ（１，ｔ）￡＞０．

原方程的初始条件也相应的化为：

舶＝ｐ扛，０）＝ｗｚ（ｘ）＋ｔ吨＠），ｚ∈（０，１），ｑ；Ｄ＝口扛，０）＝饥０）一ｔ吨０），ｚ∈（０，１），，阳＝，７（ｚ，０）＝≯（一丁ｚ），ｚ∈（０＇１），ｒ０＝ｒ（ｘ，０）＝妒（一下ｚ），ｚ∈（０，１），ｓｏ＝ｓ（ｘ，０）＝≯（一７．）＋妒（一７．），ｚ∈（０，１），Ｙｏ＝ｙ（ｘ，０）＝≯（一下）一妒（一７．），ｏ∈（０，１）．

定义内积空间（Ｈｉｌｂｅｒｔ空ｌ＇ｆｉ－Ｊ）：

咒＝Ｌ２（ｏ，１）ＸＬ２（ｏ，１）ＸＬ２（ｏ，１）×Ｌ２（ｏ，１）×Ｌ２（ｏ，１）×Ｌ２（ｏ，１）１１（２．３）ｃ２．４，（２．５）（２．６）

上述空间中的内积我们定义为：

＜＜叭，叭，＞＝Ｚ１一＋Ｚ１）一ｑ２（ｘ）ｄｗ２＞＝／ｐｌ（ｘ）ｐ２（ｘ）ｄｘ

ＪＱ＋／ｑｚＪＱＣｘ）ｑ２（ｘ）ｄｘ－Ｉ－Ｚ１“。）瓣Ｊｏ／＇７ｌ（。），７２（ｚ）血

＋Ｚ１州ｚ）瓣ｚ＋ｆＯ８１（ｚ）珊＋Ｚ１删瓣

其中瞅＝Ｐｉ，吼，仇，ｒｔ，ｓｉ，玑）Ｔ∈７－１，ｉ＝ｌ，２．一

在饨空间中定义一算子Ａ，则其定义域为：

．

Ｄ（Ａ）＝｛（ｕ，＂，Ｗ，ｋ，ｒｎ，ｎ）Ｔ∈【Ｈ１（ｏ，１）】６Ｉ乱（ｏ）＝ｕ（ｏ），ｎ（ｏ）＝ｍ（ｏ），伽（ｏ）＝ｐ（１），，ｏＩ．，Ｊ－ｚ７、

七（ｏ）＝ｑＯ），乱（１）＋口（１）＝－ｋｅ酊陋（１）一后（１）一口－『苫（ｍ０）＋佗０））出】）

上式中的月１（Ｏ，１）爱不一阶累伯列夫（Ｓｏｂｏｌｅｖ）空同．

下面我们定义算子以为：

Ａ（ｕ，ｕ，叫，七，ｍ，ｎ）Ｔ＝（五ｄｕ，一五ｄｖ，一孑１五ｄｗ，孑１五ｄｋ，面ｄｍ，一五ａｎ）ｒ，（让，ｕ，叫，免，ｍ，仡）Ｔ∈Ｄ（Ａ）（２．８）有了上述准备以后，我们将方程（２．２）化为抽象的柯西（Ｃａｕｃｈｙ）问题：

｛未叭幻刊叭幻。刈（２．９）

【ｗ（ｏ）＝％．

其中Ⅳ（￡），Ｗｏ分别表示空间？－Ｉ中的函数和已知定点，在上方程中控件变量ｚ被隐化了，即

１ｗ（ｔ）＝ｗ（ｘ，ｔ）＝（ｐ（ｚ，￡），ｑ（ｘ，￡），刀（ｚ，ｔ），ｒ（ｘ，ｔ），ｓ（ｘ，￡），ｙ（ｚ，￡））Ｔ

Ｉ％＝（Ｐｏ，ｑｏ，ｒ／ｏ，ｒｏ，８０，ｙｏ）Ｔ

上式中的Ｐｏ，ｑｏ，伽，ｒｏ，８０，Ｙｏ是由（２．６）所确定的．

２．２系统岛半群的可生成性

为了证明系统算子以生成岛半群，需要引入下列定理．

定理２．１设Ａ由（２．７）和（２．８）所定义的，则Ａ是咒上的闭稠定算子，且具有预解紧（算子的预解式是紧算子）．１２

证明：由Ａ的定义，利用偏微分算子的边值性，可得Ａ是一个闭稠定算子．下设Ａ∈Ｃ，在空间饨中考虑预解方程，任取Ｇ＝（ｇｌ，９２，ｇｓ，９４，９５，９６）Ｔ∈咒，求解方程：

（Ａ，一Ａ）Ｆ＝Ｇ，Ｆ＝（ｆｌ，ｆ２，ｆ３，＾，／＇５，ｆ８）∈Ｄ（Ａ）

即

Ａ＾（ｚ）一掣＝夕－（ｚ），

入厶（ｚ）＋掣＝卯（ｚ），

入ｒ＾（ｚ）＋掣＝７－９３（ｚ），

＾（ｏ）＝ｆ２（ｏ），Ａ（ｏ）＝ｆｄｏ）

，３（ｏ）＝＾（１），＾（ｏ）＝ｆ２（１）

ｆ１（１）＋ｆ２（１）＝－ｋｅ盯【＾（１）一ｆ４（１）一ｎＪ孑（＾０）＋＾０））出】．

解上常微分方程组可得：

＾０）＝＾（ｏ）ｅｈ—ｆｏｅＡ伍～）ｇｌ（ｓ）ｄｓ，

＾（ｚ）＝厶（ｏ）ｅ—ｈ＋ｆｏ＂ｅ—Ａ（２一?）９２（ｓ）ｄｓ，

＾０）＝＾（ｏ）ｅ以住＋丁譬ｅ一打忙一）９３（ｓ）ｄ８，

ｆｄ＝）＝＾（ｏ）一佗一丁厅ｅ打（扣。）９４Ｃｓ）ｃｌｓ，

＾＠）＝＾（ｏ）ｅｈ—Ｊ孑ｅＡ佃一）ｇｓ（ｓ）ｄｓ，

＾（ｚ）＝ｆｄｏ）ｅ一＿、ｚ＋ｆｏｅ—Ａ（卫一。）ｇｄｓ）ｄｓ．

由上述方程组可知：

＾（１）＝＾（ｏ）一一詹ｅＡ（１－。’９ｌ（ｓ）ｄｓ，

厶（１）＝厶（ｏ）ｅ以＋詹ｅ－．ｘ（１－。）９２Ｃｓ）ｄｓ，

＾（１）＝＾（ｏ）ｅ以ｒ＋下詹ｅ以ｒ（１－＂）９３Ｃｓ）ｄｓ，

ｆｄｔ）＝＾（ｏ）ｅｈ—ｒ片ｅｈ（１－。）９４Ｃｓ）ｄｓ，

＾（１）＝＾（ｏ矽一詹ｅＡ（１－?）ｇｓＣｓ）ｄ８，

＾（１）＝，６（ｏ）Ｂ一＾＋ｆｏ＇ｅ—Ａ（１～）ｇｓＣｓ）ｄ８．

１３（２．１０）（２．１１）（２．１２）

将微分方程的边界条件代入上式，则有：

盯ｌ＾（１）一＾（１）一口／（＾（ｚ）＋＾（ｚ））出Ｉ＝－ｋｅ盯［脚）一，４（１）一．石０２（脚）＋脚））出】＝

ｏ．，Ｊ

１１

＝一七ｅ８ｒ［＾（。）ｅ－ＡＩ＂＿＾（。）ｅＡ＊４－ｒ

＝一七ｅｄ下［＾（。）ｅ－Ａ，＂－Ｆ７＂１ｅＡ（１－ｓ）９３（ｓ）ｄｓ＋ｒｚｅ－－Ｍｌ－ｓ）９４（ｓ）ｄｓ．＋一口厂１（删ｅｈ＋删ｅ砒一厂霉“一一口／（＾（ｏ）ｅｈ＋＾（ｏ）ｅ以ｚ一／矿ｏ＿Ｊ０Ｊ／ｓｄ）ｓ（ｓＪｏｇ））ｓ－ｚＭ＋＇ｔ－Ｊｏｅ夕６（ｓ）ｄｓ）如Ｉ卯（ｓ）ｄｓ）如］Ｊｅ－Ａ１＂（１－ｓ）９３（ｓ）ｄｓ一＾（。）ｅＡ下＋丁１ｅＡｒ（１－ｓ）肌（ｓ）ｄｓ

一口Ｚ１（＾（。）ｅｈ＋＾（。）ｅ—ｈ）血＋ｎ（／０１Ｊ【ＯｚｅＡ（ｚ－ｓ）舶（ｓ）ｄｓ血一／０１Ｚ￡ｅ。ｃ霉＿｜）卯（ｓ）ｄｓ血）］＝一七ｅ盯Ｉｌｌ（。）（ｅ（１一，Ｉ）一妥）（ｅＡ—ｅ—Ａ）二ｅ—Ａｒｆ０１ｅＡＯ－Ｓ）９１（ｓ）ｄｓ

＋ｅＡｒ［１ｅ—Ａ（１一?）夕２（ｓ）ｄｓ＋７．［１ｅ—Ａｒ（１一?）夕３（ｓ）ｄｓ＋７．［１ｅ＾，．（１一｜）９４（ｓ）ｄｓ

．，Ｏ．，０．，Ｏ

＋＋ｎ（／０１ｆｆｅＸ（＝－?）ｇｓ（ｓ，ａｓ一／０１Ｚ０ｚｅ－Ａ（ｚ－ｓ）卯ｃｓ，ｄｓ，叫替换＾（１），厶（１）可得：

１

加）（ｅ～ｅ以）一ｆｏｅＡＯ－－）９１（ｓ）ｄｓ＋Ｚ１ｅ以（１叫姒ｓ）ｄｓ

．，Ｏ

：一七ｅ口ｒ『＾（ｏ）（ｅ（１一，．）一詈）（ｅ▲一ｅ—Ａ）一ｅ—Ａ，．／‘ｅ＾（１一?）９ｌ（ｓ）ｄｓＬ＾Ｊｏ

ｆｏＩｅ－ＡＯ－．）卯（ｓ）ｄｓ＋ｒｆＯｅ－－Ａｔ（１－ｓ）卯（ｓ）ｄｓ＋ｒｆＯ

＋ｎ（／０１ｆｅ谁叫小灿一／０１Ｊ００＝ｅ－Ａ（ｚ－ｓ）９６㈤㈣叫＋ｅＡｒｅＡ，．（１－ｓ）肌（ｓ）ｄｓ

移项可得：

＝１＾（ｏ）（ｅＡ＋ｅ一＾）＋七ｅ口ｒ［＾（ｏ）（ｅ（１一ｒ’一妥）（矿一ｅ一＾）】ｅＸ（Ｘ－Ｓ）ｇ］（ｓ）ｄｓ—ＺｏＩｅ－Ａ（１－ｓ）９２（ｓ）ｄｓ－ｋｅ＝ｒ［ｅＡｒＺ１ｅ—ｉｃｌ一＿，夕ｚ（ｓ）ｄｓ

１Ｉ

ｆｏｅ－，Ｘ１＇Ｏ－．）９３（ｓ）ｄｓ＋ｒＺＩｅ州１。｜）９４（ｓ）ｄｓ

＋口ｃＺｌＺ薯ｅＡｃ２一?，卯ｃｓ，ｄｓ一／０１Ｊ二ｏ＝ｅ－ｘ（＝－ｓ）９６ｃｓ，ｄｓ，ｄｚ］－ｅ－ｈｅｘＯ－?）９１（ｓ）ｄｓ＋ｒ

１４

即有：

２／ｌ（Ｏ）（ｃｏｓｈＡ＋ｋｅ酊（ｅ‘１。ｒ’一妥）８ｉｎｈ入）

＝＝Ｚ１ｅＡｃｌ一?，夕，（ｓ）ｄｓ—ＪＣｅ－Ａ（１－＇）９２（ｓ）ｄｓ－ｋｅａｒ［ｅ＾ｒＺ１ｅ—Ａｃｌ一?，９２（ｓ）ｄｓ

１

＿ｅ＿ｈＺ１“ｈ讯）ｄｓ＋ｒｅ－Ａ１＇（１－＇）９３（ｓ）ｄｓ＋ｒＺ１矿（１。｜）９４（ｓ）ｄｓ

１

＋ｎｃＺｌＺＯ＝ｅＭ＝－ｓ）ｇｓｃｓ，ｄｓ一／ｏＺＯ＝ｅ－Ａ（＝－ｓ）卯ｃｓ，ｄｓ，ｄ叫

我们记△（Ａ）＝ｃｏｓｈＡ＋ｋｅｄｒ（ｅ（１一ｒ）一妥）ｓｉｎｈＡ，当Ａ（Ａ）≠０时，我们可得：＾（ｏ）＝邳１ｎＪ。１一（１一。）夕ｌ（ｓ）ｄｓ一层ｅ—Ａ（１一。）夕２（ｓ）ｄｓ—ｋｅａ７【ｅＡｒ詹ｅ－Ａ（１一。）９２（ｓ）ｄｓ

—ｅ－Ａ．ｒ詹ｅＡ（１一。）夕１（ｓ）ｄｓ＋ｒｆ孑ｅ一＾ｒ（１一。）９３（ｓ）ｄｓ＋ｒｆｌｏｅＡｒ（１一＊）９４（ｓ）ｄｓ（２．１３）＋口（片厅矿（霉一）ｇｓ（ｓ）ｄｓ一启后ｅ—Ａ（扣。）ｇｓ（ｓ）ｄｓ）ｄｚ】）．

利用＾（１），ｆ２（１）的表达式，可得＾（ｏ），＾（ｏ）为

ｆ３（０）＝＾（１）＝＾（ｏ）一一詹一（１一．）９１（ｓ）ｄｓ（２．１４）

１４（０）＝ｆ２（１）＝正（ｏ）ｅ一▲＋詹ｅ－Ａ（１一?）９２（ｓ）ｄｓ

因此，当△（入）≠０时，入∈ｐ（Ａ），＾（０）＝厶（ｏ）＝Ａ（ｏ）＝＾（ｏ），Ａ（ｏ）＝＾（１），Ａ（ｏ）＝ｆ２（１）可唯一表示，即有：

＾（ｏ）ｅｈ一片一（ｐ。）ｇｌ（ｓ）ｄｓ

厶（ｏ）ｅ—ｋ＋詹ｅ以（１－＂）９２（ｓ）ｄｓ

Ｆ＝（＾，厶，＾，＾，＾，＾）Ｔ＝Ｒ（入，Ａ）Ｇ＝矗（ｏ）ｅ以ｒ霉＋丁片ｅ以ｒ任ｑ）ｇｓ（ｓ）ｄｓ（２．１５）

＾（ｏ）ｅｈ卫一７．片ｅｈ（霉－。）９４（ｓ）ｄｓ

＾（ｏ）ｅ妇一片ｅＡ（卜。）ｇｓ（ｓ）ｄｓ

＾（ｏ）ｅ一妇＋譬ｅ以（扣。）９６（ｓ）ｄｓ

其中＾（ｏ），＾（ｏ），＾（ｏ），＾（ｏ），＾（ｏ），ｆ６（ｏ）由（２．１３），（２．１４）给出．由上可知，兄（Ａ，Ａ）是咒的有界线性算子，再由Ｓｏｂｏｌｅｖ嵌入定理可知，Ｒ（Ａ，Ａ）是７１上的紧算子．定理２．２由上所定义的算子Ａ生成一个岛半群．１５

证明：首先为了证明Ａ生成一个岛半群，我们需在咒上引入一个新的内积：＜肌，％＞ｌ＝ｆｏｅａｘｐｌ（ｚ）一ｐ２（ｘ）ｄｚ＋Ｚ１扩“。）瓣＋Ｚ１ｅ吲ｚ）瓣ｚ

＋Ｚ１∥，．－（ｚ）；丽出＋Ｚ１铲ｓ－（ｚ）珊＋ｆｏｅｐ＇ｙ１（ｚ）函两如

其中姒＝慨，啦，班，ｒｉ，８ｉ，玑）Ｔ∈７１，ｉ＝１，２，Ｑ，卢，，ｙ，（，专，ｙ∈Ｒ．

可证得新的内积与原内积是等价的．（即诱导的范数等价：：，ｌｌＷｌＩ≤ＩＩⅣ１１１≤ｃ２１１ｗ

ＩＩＷＩＩ－＝Ｚ１ｅ凹ｐ（ｚ）丽血＋Ｚ１ｅ肚ｇ（ｚ）丽血＋Ｚ１ｅ＂７７（ｚ）而＿ｄｚ

＋Ｚ１铲心）珊＋／０１扩出）珊＋Ｚ１ｅ吲ｚ）珊ｚ

Ｚ０１ｑ（ｚ）孤＋Ｚ１咖）珊

＋小ｚ）砷¨Ｚ１ｓ（二）珊＋／０１ｙ（ｚ）而ｌｄ。

所以有

ｌ

ｖ（ｚ）２出＋Ｚ１口（ｚ）２出＋Ｚ１叩（ｚ）２血＋Ｚ１ｒ（ｚ）２出＋Ｚ１ｓ（ｚ）２出＋ｆｏＩｙ（ｚ）２妇≤ＩＩＷＩＩ－≤ｆｏｅ口ｐ（ｚ）２血＋Ｚ１ｅ卢口（ｚ）２出＋／０１矿’７（ｚ）２血＋ｆｏＩｅｃｒ（ｚ）２血

＋Ｚ１≠ｓ（ｚ）２如＋Ｚ１ｅｙ秒（ｚ）２血≤ｍ舣｛ｅａ，ｅ口，矿，ｅ‘，ｅ‘，ｅｐ）（Ｚ１ｐ（ｚ）２血＋ｆ０１ｑ（ｚ）２如＋Ｚ１叩（ｚ）２ｄｚ＋Ｚ１ｒ（ｚ）２ｄｚ＋／０１ｓ（ｚ）２ｄｚ＋Ｚ１矽（ｚ）２ｄｚ）即ＩＩＷＩＩ≤１１ｗＩＩｌ≤ｍａｘ｛ｅａ，ｅ卢，ｅ１｝ｌｌＷＩＩ，等价．）在此内积下，对任意的实向量Ｗ＝０，ｑ，７７）Ｔ∈口（Ａ），我们有

（以眦ｗ）１＝Ｚ１ｅ∞丽掣出一ｆｏ＇¨｛Ｚ１ｅ＂而掣如

＋导ｐ雨掣血＋Ｚ１伊羽掣血一产王丽掣如

Ｊ０／俨而酌ｐ（ｚ）一／ｅ触而＿ｄｇ（ｚ）一兰／扩而＿ｄ７７（ｚ）Ｊ０ＴＪｏ

＋＿．ｐ丽ｄｒ（卅．ｐ珊啦）－．石１ｅ坩瓣出）１６

，上，且１

２主（ｅ∞矿（ｚ）１５一口Ｚ１０１）＠２７，＂ｅ李一￥ｄ）ｚ（２ｑ触ｅ上卢＋ｌ０１）ｚ（２口触ｅ一如）ｚ（２ｐ∞ｅ

＋手Ｚ１ｅ唧㈤¨≯２㈤１３－享Ｚ１钟州卅鲋㈤１５＿ｆＺ１舢州ｚ

，工

一ｅＶＺｙ２（ｚ）皓＋ｐ／ｅ昭可２（ｘ）ｄｘ）

Ｊｏ。

二三（ｅ口ｐ２（１）－－ｅ卢ｑ２（１）一了ｅ７叼２（１）＋导叩２（０）＋等ｒ２（１）一｛ｒ２（ｏ）＋ｅ‘ｓ２（１）－ｅｐｙ２（１））

＋三（一口Ｚ１ｅ∞ｐ２（ｚ）ｄｚ＋＃ＪＣｅ卢＝ｑ２（ｚ）ｄｚ＋罟Ｚ１ｅ＂刀２（ｚ）ｄｚ一摹Ｚ１ｅｃ￡ｒ２（ｚ）ｄｚ）

’一上０１ｅＣ＝ｓ２（壮＋ｙＺ１ｅ吁㈤血

箕中

ｅａｐ２（１）－－ｅ卢ｑ２（１）一等张１）＋轫０）＋等ｒ２（１）一扣０）＋ｅ‘ｓ２（１）－ｅｐｙ２（１）

／＝（ｅ口＋孑１）ｐ２（１）一（矿＋季）９２（１）一等，７２（１）＋等ｒ２（１）＋ｅ‘ｓ２（１）－ｅｐｙ２（１），

选取适当的Ｑ，卢，７，（，∈，ｌ，，总可以使得（矿＋；）矿（１）一（ｅ口＋寻）９２（１）一等，７２（１）＋等ｒ２（１）＋ｚｓ２（１）一ｅＶｙ２（１）＜０成立，再令Ｍ＝ｍａｘ｛一爰，鲁，丢，一丢，一ｌ，盖），可得

（ＡＷ，Ｗ）Ｉ≤ＭＩＩＷＩＩｉ

从而，可以得到Ａ—Ｍ，是耗散算子，注意到当Ａ＞０时，△（Ａ）＞０，Ｒ（入，一Ａ）＝Ｗ，利用Ｌｕｍｍｅｒ－Ｐｈｉｌｉｐｓ定理１１０］，Ａ—ＭＩ生成一个岛压缩半群，故Ａ生成一个岛半群．２．３系统算子Ａ的谱分析

定理２．３设Ａ由（２．７），（２．８）所定义，则月的谱特征方程为：

Ａ（Ａ）＝ｃｏｓｈ入＋七ｅ盯（ｅ‘ｌ－札妥）ｓｉｎｈＡ＝０

仃（Ａ）＝ａｐ（Ａ）＝｛Ａ∈Ｃｌ△（Ａ）＝ｏ）．且对每个特征值Ａ∈唧（以），其相应的特征空间维数均为１．

证明：由定理（２．１），系统算子Ａ是闭稠定的且具预解紧，又由离散算子的定义可知：

Ａ是离散的，从而仃（以）＝唧（／Ｉ）．对任意的Ａ∈盯（／ｔ），我们考察月的特征方程：

１７

ＡＷ＝ＡＷ，Ｗ＝扫，ｑ，，７，ｒ，８，∥）Ｔ∈口（Ａ），ａｐ：

入ｐＣｘ）＝蚴ｄｘ

柚（ｚ）＝一掣

加（ｚ）＝一；掣

Ａｒ（ｘ）＝三业ｄｘ

沁（ｚ）＝蚴ｄｚ

蛔（ｚ）＝一掣

边界条件为：（２．１６）

ｌｐ（ｏ）＝ｇ（ｏ），ｓ（ｏ）＝Ⅳ（ｏ）

｛，７（ｏ）＝ｐ（１），７Ｉ（ｏ）＝口（１）

ｌｐ（１）＋ｑ（１）＝一ｋｅ口ｒ切（１）一ｒ（１）一口Ｊ：（ｓ（ｚ）＋可（ｚ））出】

ｐ（ｚ）２ｐ（ｏ）ｅｈ，口（ｚ）２口（ｏ）ｅ—ｋ，刀（ｚ）２，７（ｏ）ｅ－Ａｖ￡（２．１７）Ａｎ∈ａＣＡ）＝ａｐ（Ａ）时，集合｛冗ｅＡＩ△（Ａｎ）＝ｏ）有界的，且舰ＩｍＡｎ＝ｏｏ?进一步我们有，

证明：设△（入）＝ｃｏｓｈ入＋ｋｅ。ｒ（ｅ（１－１＂）一妥）ｓｉｎｈ入，利用定理２．１，我们知道，Ａ具有预解紧，从而Ａ是离散的，即Ａ的谱点为可数的有限重的孤立本征值，而在任意有限区域内Ａ的谱点均是个数有限的．又因为Ａ是岛半群的生成元，由Ｈｉｌｌｅ－Ｙｏｓｉｄａ条件可得，△（Ａ）的零点必位于某平行于虚轴的具有有限宽度的垂直带域里，故可得复数集合（ＲｅＡ住ＩＡ（Ａｎ）＝ｏ）是有界的，且有舰ＩｍＡｎ＝ＣＯ?

下面我们来讨论／ｘ（一ｘ）的零点重数．设ｆ为．／ｘ（，ｘ）的零点，则有

△（专）＝ｃｏｓｈ专＋七ｅ酊（ｅ（１－Ｉ＂）一芸）ｓｉｎｈｆ＝０

＇．

对△（Ａ）求导得

△’（入）＝ｓｉｎｈＡ＋ｋ∥（ｅ‘ｌ－，．’一妥）∞ｓｈＡ＋ｋｅ酊景ｓｉｎｈ入

＝（七∥景＋１）ｓｉｎｈ入＋七∥（ｅ‘ｌ－ｆ’一妥）ｃｏｓｈＡ

再次求导，可得

△”（Ａ）＝一２七ｅ酊§ｓｉｎｈＡ＋（ｋｅ酊景＋１）ｃｏｓｈＡ＋ｋｅ盯螽ｃｏｓｈ入

帐酊沁－ｒ’一妥）ｓｉｎｈ入

＝七ｅ。７（ｅＯ－－）一妥一耳２ａ）ｓｉｌｌｌｌＡ＋（七ｅ”甭２（２＋１）ｃｏｓｈＡ

由（２．１８）可知：

ｃｏｓｈ∈＝此盯（ｅ（１町’一詈）ｓｉｎｈ∈

再将∈代入△。（Ａ）中，利用式（２．１８）有

△’＠）＝【ｋａｌ＂万ａ＋１）ｓｉｎｈｆ＋尼ｅ盯（ｅ（１一ｒ）一；）ｃｏｓｈ∈

．＝（树ｒ吕＋１）８ｉｎｈｆ—ｋｅ２ａ．，＂（ｅ（１＿ｔ）一；）２ｓｉｎｈｆ

＝（七ｅ盯三＋１一ｋｅ２ａ１＂（ｅ（１吖）一；）２）ｓｉｎｈｆ

注意到ｚｘ（Ａ）＝０可知ｓｉｎｈ∈≠０．而有Ａ’（∈）＝０，则有

树ｒ虿ｎ＋ｌ埘芦（ｅ（１吖’一詈）２＝ｏ

１９（２．１８）（２．１９）

＝七ｅｄｒ（ｅ（１一＇．Ｌ虿ａ一可２ａ）ｓｉＩｌｈ莓＋（七ｅ盯虿２ａ＋１）七ｅｄｒ（ｅ（１一ｒ）一虿ａ）ｓｉｎｈｆ＝七ｅ盯【ｅ（１＿ｒ）一詈一虿２ａ一（尼ｅ酊虿２ａ＋１）（ｅ（１卅一詈）】ｓｉＩ山∈又因为ｓｉｎｈｆ≠０，所以有

ｅ（１卅一詈一≯２ａ一（胪虿２ｎ＋１）（ｅｆＸ－－）＿詈）＝。

整理可得

古（七矿ｅａｒ－－ａ）一七口ｅ口ｒｅｔｌ—ｒ，占＝。

即

１

一＝?－?＿＿＿＿＿＿＿?－＿＿＿－一ｋｅａｌ＇ｅ（１一＇．）

ｆｋａｅ酊一１

（２．２０）没有相等的解时，则有△’（入）≠０，即△（入）的零点是单重的．上式和（２．２０）矛盾．故有（２．２１），我们可以得到△（入）的零点重数至多为２．且当（２．１９）与

第三章弦振动时滞阻尼系统的稳定性分析

用于证明系统稳定性的方法很多，比如证明系统的谱确定增长假设成立，以及频域乘子法．但对于无穷维的系统来说，系统算子对系统性质的刻画，最为深刻的性质是系统算子的广义本征元构成状态空间的无条件基，而在Ｈｉｌｂｅｒｔ空间中，这就是系统的Ｒｉｅｓｚ基的存在性．本章就是采用Ｒｉｅｓｚ基方法证明系统的指数稳定性，首先我们证明系统算子Ａ的广义特征向量组的完备性，即构成了空间的Ｒｉｅｓｚ基，我们引入下命题．

命题３．１Ｂｇ］设Ａ是Ｈｉｌｂｅｒｔ空间咒中的某岛半群的生成元．再设Ａ是离散算子，且对其伴随算子Ａ’，当ＡＥｐ（Ａ‘）时，Ｒ（Ａ，Ａ‘）具有如下形式：

砌∥）ｙ＿错Ｖｙ∈７４

这里，对任意的Ｙ∈咒，Ｇ（入）ｙ是一全纯Ｈ－值函数，其增长阶不超过ｐｌ；而Ｆｐ，）是一数量全纯函数，其增长阶为伪．令Ｐ＝ｍａｘ｛ｐ１，助）＜∞，并取得ｎ使得ｎ一１≤Ｐ＜ｎ．如果在复平面上存在ｎ＋１条射线：∞，Ｊ＝０，ｌ，２…．，ｎ，其幅角满足：

ｏ２＝ｉ７ｒ＜ｉ＜ａｘｇＴｌＴ＜ａｘ９７２＜…＜ｇａｒｇＴ．ｒ２‘２，且一３２Ｅ，且ａｒｇＴｊ＋１ａ一缸ｇ∞Ｓ元，一ａｒｇ∞≤要，ｏｊ＜ｎ

使得冗（入，Ａ‘）ｙ对任意的ＹＥ７４，当…ｊｏｏ时，每条射线∞（０＜Ｊ＜佗）均是有界的，则有结论：Ｓｐ（Ａ）＝饨，其中Ｓｐ（Ａ）＝咒表示Ａ的所有广义本征元（根向量）张成的线性闭子空间．

注：若，（ｚ）满足下条件的全纯函数

Ｉ，（ｚ）ＩＳＡｅ引叫Ｖ名∈Ｃ（３．１）

其中，常数Ａ，Ｂ均为正的，则满足上条件的最小正数Ｂ就称为函数，（ｚ）的（指数型）增长阶１１９】，例．

利用命题３．１，我们可以证得下述结论：

定理３．１设Ａ是由（２．７）和（２．８）所定义的，则有Ａ的广义本征元在咒中是完全的，即Ｓｐ（Ａ）＝咒．２１

证明：由题意我们易得，只须证明Ａ满足命题３．１的条ｆＩ：ＢＰ可．则Ｆｈ共轭算子的定义＜Ａｘ，Ｙ＞＝＜ｚ，Ａ‘Ｙ＞，可求得Ａ。的定义域为：

口（月‘）＝｛（ｐ，ｇ，，７）Ｔ∈（日１（ｏ，１））３Ｉｐ（Ｏ）２口（ｏ），ｓ（ｏ）２可（ｏ），ｒ（１）２７７（１）＝ｓ（１）（３．２）

＝ｙ（１）＝０，叩（ｏ）＝－＇ｒｐ（１），ｒ（ｏ）＝－－ｒｑ（１）｝

以?的表达式为：

Ａ’。，口，叼，ｒ，ｓ，可）Ｔ＝（一塞，塞，季塞，一季塞，一塞，塞）Ｔ，Ｖ∞，口，叼，，．，ｓ，ｙ）Ｔ∈Ｄ（Ａ‘）（３－３）对任意的入∈ｐ（Ａ’），Ｙ＝（Ｙ１，ｙ２，Ｙ３，ｙ４，ｙ５，珈）Ｔ∈咒．我们考虑Ａ。的预解方程：

（入Ｊ—Ａ）Ｗ＝ＫＷ＝∞，ｑ，，７，，．，ｓ，ｙ）Ｔ∈Ｄ（Ａ’）

即

却（ｚ）＋蚴ｄｚ＝∥１（ｚ）

Ａｇ（ｚ）一业ｄｚ＝抛（ｚ）

入丁，７（ｚ）一业ｄｚ＝丁钠（ｚ）

入ｒｒ（ｚ）＋蚴ｄｚ＝７．玑（ｚ）

入ｓ（ｚ）＋业ｄｚ＝ｙｄｘ）

入可（ｚ）一生掣＝蜘（ｚ）

边界条件为：（３．４）

（０）＝口（ｏ），８（０）＝ｙ（ｏ）

（１）＝，７（１）＝８（１）＝ｙ（ｚ）＝０

（０）＝一叩（１）

（０）＝－－ｒｑ（１）

解微分方程（３．４）可得

ｐ（ｚ）＝ｐ（Ｏ）ｅ—ｈ＋－『孑ｅ－Ｍｚ一。’ｙｌ（ｓ）ｄｓ

ｑ（ｘ）＝口（ｏ）ｅ蛔一厅ｅＡ（霉ｑ）ｙ２（ｓ）ｄｓ

删＝删ｅ№一ｒ譬扩‘…伽）凼

，．（ｚ）＝，＇（ｏ）ｅ一概＋７．片ｅ—Ａ，．（。一?）ｙ４（ｓ）ｄｓ

ｓ（ｚ）＝ｓ（ｏ）ｅ—ｈ＋ｆｅ以（扣。）ｙｓ（ｓ）ｄｓ（３．５）‘。

ｙ（ｚ）＝ｙ（ｏ）ｅｈ一后ｅＡ（扣。）ｙｓ（ｓ）ｄｓ２２

利用边界条件，证明方法与定理２．１类似，通过一系列的化简，我们可以求得Ａ＋的预解表达式为：

ｐ（ｏ）ｅ一妇＋譬ｅ以（扣。）ｙｌ（ｓ）ｄｓ

口（ｏ）ｅ妇一ｆ∥（ｐ。）ｙ２（ｓ）ｄｓ

Ｗ＝（Ｐ，口，７７，’．，ｓ，ｙ）Ｔ＝Ｒ（入，Ａ’）ｙ＝叩（ｏ）ｅＡ侣一７．譬ｅｈ（扣。）ｙａ（ｓ）ｄｓ

ｒ（ｏ）ｅ以ｒ２＋７－岳ｅ以ｒ（扣?）ｙ４（ｓ）ｄｓ

ｓ（ｏ）ｅ砒＋厅ｅ以（扣。）ｙｓ（ｓ）ｄｓ

∥（ｏ）ｅｋ一片ｅＡ（ｐ。）ｙ６（ｓ）ｄｓ

其中ｐ（ｏ）＝ｇ（ｏ），４０）＝掣（ｏ），，７（ｏ）＝ｐ（１），Ｋｏ）＝ｑ（ｔ）都可以被确定．

注：△（入）冗（入，Ａ’）ｙ是增长阶数有限（Ｐ≤２）的指数型Ｈ－值全纯函数，用Ｇ（入）ｙ表示．从而有：

砌∥肛搿Ｖ撕（∽．．

由前知Ａ生成一个岛半群，即Ａ的谱集必是位于某平行于虚轴的有限宽度的垂直带域里，从而对充分大的正实数Ｍ，我们可以取三条射线：饥＝一Ｍ＋ｉ凡，仇＝一Ｍ—ｉ风，及＂／ａ＝一Ｍ—ｔ再～．显然，Ｒ（入，Ａ’）ｙ在每一条射线上一致有界．因此命题３．１的全部条件都得到了验证．

为了证明本章的主要结论：Ａ的广义本征元系组成咒的一组ｍ嗽基，我们再引入下命题：

命题３．２１２１】设咒是可分Ｈｉｌｂｅｒｔ空间，Ａ是某岛半群Ｔ（ｔ）的生成元，且满足以下条件：．

１）－（－）＝ａｌ（Ａ）Ｕ啦（Ａ），其中ａ２（Ａ）＝｛Ａ七）是１是由Ａ的孤立的有限几何重数的本征值所构成．

２）ｓｕｐｍ口（ｈ）＜ＯＯ，其中ｍ口（入七）＝ｄｉｍＥ（Ａ七，Ａ）ｎ，而Ｅ（ｈ，Ａ）表示Ａ的相应于ｈ的Ｒｉｅｓｚ投影子，它由ｈ对应的根子空间所确定．

３）存在常数０ｆ，使得８ｕｐ．【Ｒｅ入ｌＡ∈仃ｌ（Ａ）｝≤ａ≤ｉｎｆ｛ＲｅＡｌ入∈ｃｒ２（Ａ）’

．及一ｉｎｆ．．Ｉ入ｎ—ｋＩ＞０ｒｌ≠ｍ。（３．６）成立．则可得下述结论：ｉ）必存在两个Ｔ（￡）一不变子空间丸１和７如满足性质仃（ＡＩ咒，）＝０＂１（Ａ）和盯（Ａ１７ｔ：）＝ａ２（Ａ），而且｛Ｅ（Ａ七，Ａ）咒２）芒１组成咒２的一组子空间Ｐｄｅｓｚ基，进一步

ｉｉ）如果ｓｕｐＩＩＥ（Ａ七，Ａ）Ｊｌ＜ｏｏ，那么

七２１

Ｄ（Ａ）ｃ７ｔｌｏ７ｔ２ｃ咒．

ｉｉｉ）饨具有下列分解：

当且仅当ｓｕｐｌｌ∑Ｅ（Ａｈ，Ａ）ＩＩ＜Ｏｏ成立．

注：我们将Ａ离散谱点集｛入ｎＩ佗∈Ⅳ，ｃａ２（Ａ）满足的条件（３．６），称之为Ａ的谱集

ａ２（Ａ）具有可分离性（ｓｅｐａｔａｔｅｄｎｅｓｓ）．

命题３．３（见文【１９】定理３）设／（ｚ）满足（３．１）的增长阶有限的全纯函数，且其在实轴上

有界，／（ｚ）的孤立零点Ａｎ，ｎ∈Ｎ满足条件：

ｓｕｐＩＩｍＡｎＩ＝ｈ＜ｏｏ，ｓｕｐｍ，Ｉ＜ｏＯ（３．７）

ｎｎ

这里的ｍ，。表示入ｎ作为／（ｚ）的零点阶数．则当ｉＩｌｆＩ，（‰）（ｋ）Ｉ＞０时，｛Ａｎｌｎ∈Ｊｖ）可分离，即有ｉ啦ｌＡｎ—ＡｍＩ＞０成立．ｎ≠ｍ

下面我们给出本章的主要定理：

…

定理３．２设Ａ是由（２．７）和（２．８）所定义的系统算子，则＾的广义本征元系构成咒的

一组Ｒｉｅｓｚ基．证明：欲证此定理结论成立，我们只须验证命题３．２的三组条件成立即可．

我们取ａｌ（Ａ）＝１２Ｉ及ａ２（Ａ）＝盯（Ａ）．定理２．３和定理２．４表明命题３．２的前两个条件成立．至于命题的第三个条件，由Ａ生成岛半群，可知存在充分大的Ｍ＞０使得

一ｏｏ圭ｓｕｐ｛ＲｅＡＩＡ∈ａｌ（Ａ）＝１２Ｉ）≤Ｑ圭一Ｍ≤ｉＩｌｆ｛＆入ＩＡ∈ｃｒ２（Ａ））

至此，欲证明Ａ的广义本征元系构成咒的一组ＲＪｅｓｚ基，关键就是在于证明Ａ的谱集具有可分离性，即（３．６）成立．从而只须构造满足命题３．３条件的／（ｚ）即可．由于Ａ的本征值即△（Ａ）的零点，由定理２．３和定理２．４的结论启示，可设

，（ｚ）＝△（一ｉｚ）＝ｃｏｓｈｉｚ＋七ｅａｌ＂（ｅ（１一＇．）＋云ａ）８ｉｎｈ￡ｚ

则当△（厶）＝０时，令Ａｎ＝ｉ矗，则得，（入ｎ）＝△（矗）＝０．显然，由定理２．４知，（３．７）成

ｉｎｆｌ／（入ｎ）Ｉ＞０立，其中ｒｎｎ≤２．再直接求二阶导数，利用（２．２１）可得：Ｉ／，（Ａｎ）＞ｏｌ，ｌｉｍｎ－－＇１．∞

即ｉｎ。ｆｌｆ‘‰）（入ｎ）Ｉ＞０．

第四章弦振动时滞阻尼系统的可控性

在机器人等系统工程中，许多具有柔性结构的边界反馈控制系统一般均采用下述无穷维系统来描述：

圣（￡）＝Ａｘ（ｔ）＋阮（￡）（４．１）

其中：状态函数ｚ（￡）∈Ｈ，Ｈ是复可分的无穷维Ｈｉｌｂｅｒｔ空间，Ａ：Ｄ（Ａ）ＣＨ—Ｈ在Ｈ上生成一个岛半群Ｔ（ｔ），ｂ是一个可允许的一维输入控制算子，即ｂ可以是无界的，但应满足积分算子

／ｏＴ（ｔ—ｓ）乩（ｓ）ｄｓ，￡＞ｏ

是一个从Ｌ２（ｏ，ｔ）到Ｈ上的有界线性算子．输入函数ｕ（￡）通常设为ＬＬ（ｏ，ｏｏ）中的元．

在上面的假设下，对任意ｚｏＥＨ，ｚ（ｏ）＝ｚｏ及ｔｌＥＬＬ（０，ｏｏ），（４．１）总有唯一形式的解

ｚ（￡）＝Ｔ（￡）ｚ。＋ｆｏｔＴ（￡一ｓ）乩（ｓ）ｄｓ，￡≥。

可以证明，ｚ（?）∈ｃ（（０，ｏｏ），日），即ｚ（?）是值域在Ｈ中的连续函数【３２１．

系统（４．１）被称为是在时间【ｏ，ｑ内精确可控的，即对任意３：０ＥＨ，均存在输／ｋｉＷｉ数ＩＺｚｏＥＬ２（ｏ，ｔｏ）使得

。＝Ｔ（￡。）ｚ。＋ｊ［ｏｔＴ（ｔ—ｓ）６ｔｌ（ｓ）ｄｓ．

严格来说，上述定义的只是精确零可控性，但由于Ｔ（ｔ）是岛半群，故可知系统的精确零可控性与精确可控性等价侧．关于怎样判断系统的精确可控性的方法有很多，包括各种不动点理论及Ｂｒｏｕｗｅｒ度、重合度的理论．但是我们关心的是，怎样利用系统算子的谱、谱分析框架来刻划系统的精确可控性．下面模型中，我们利用共轭算子特征对的可分离性，最终得到了开环系统在有限时间内的精确可控性．下面我们具体讨论是系统（２．１）通过线性变换转化后的具有时滞阻尼的控制系统的精

确可控性问题，即是讨论下列系统：

爰ｐ（ｚ，ｔ）＝爱ｐ（ｚ，￡），ｚ∈（０，１），ｔ＞０

爰ｇ（ｚ，ｔ）＝一番ｇ（ｚ，￡），ｚ∈（０，１），ｔ＞０

袅叩（ｚ，ｔ）＝一彳１瓦０，７（ｚ，￡），ｚ∈（０’１），￡刈（４．２）

袅ｒ（ｚ，ｔ）＝；１∞０ｒ、．．－，￡），ｚ∈（０，１），ｔ＞０

袅ｓ（ｚ，ｔ）＝是ｓ（ｚ，￡），ｚ∈（０，１），ｔ＞０

袅可（ｚ，ｔ）＝一叠可（ｚ，ｔ），ｚ∈（０，１），ｔ＞０

系统的边界条件为：

ｐ０，￡ｑ（Ｏ，￡），４０，ｔ）＝ｙ（ｏ，￡），ｔ＞０

ｐ１，￡ｑ（１，￡）＋ｋｅｄｒｈ（１，￡）一ｒ（１，￡）一ｎＪ：（ｓ（ｚ，￡）＋可＠，￡）ｄｚ）】＝烈￡），ｔ＞０（４．３）刁０，￡ｐ（１，￡），ｒ（ｏ，ｔ）＝ｑ（１，ｔ）ｔ＞０．

其中烈￡）是系统的控制输）Ｌｉｉｔｉ数．则方程（４．２）和（４．３）可以化为如下的咒中的发展方程：

｛击叭幻酬叭￡）堋Ｄ。刈（４．４）

ＩＷ（０）＝Ｗｏ

其中ｗｃｔ）＝０（￡），ｇ（￡），，７（￡），ｒ（￡），ｓ（￡），可（￡））ｒ，ｂ＝（０，６＠一１），０，０，ｏ）Ｔ，而６０）是Ｄｉｒａｃ函数．

下面我们设系统算子Ａ满足下列条件：

１）Ａ的谱集由可数个点组成，即仃（Ａ）＝｛Ａｎ）；

２）对任意的Ａ∈盯（Ａ），入是Ａ的孤立谱点；

３）对任意的Ａ∈仃（Ａ），Ａ是Ａ的代数重数为１的本征值；

４）盯（Ａ’）＝｛石）且石均为Ａ‘的孤立的代数重数为１的本征值；５）Ｈ＝而磊而＝面磊ｉ霹巧，这里的磁，碟分别表示与／ｔ，Ａ。的本征值Ａｎ，焉相对应的谱投影算子．

注：有上述条件，我们记Ａ的谱集为｛入ｎＩ礼∈Ｎ），则有结论仃（Ａ’）＝．【石ｌｎ∈Ｎ）＝孑两，分别用‰，‰表示Ａ，Ａ‘对应于本征值入ｎ，瓦的规格化本征元．为了计算应用的

２７

简化起见，我们不妨设Ａ的谱是简单的，即／ｌ的几何重数与代数重数均为１．事实上，由定理２．４可知，Ａ的谱为点谱，它的几何重数为１，代数重数至多为２．

命题４．１（文【２２】中定理１２．２）设Ａ满足上述的条件，则系统（４．４）是精确可控的充分必要条件是Ａ。的对应于本征值石的规格化本征元系．【‰）ｎ∈Ｎ构成日的一组Ｒｉｅｓｚ基，而且有下不等式成立

’～、“

ｏ＜聪Ｉ＜６，机＞Ｉ＜ｓｎｕ∈ｐＮＪ＜礼，‰＞Ｉ＜∞?

定理４．１设＾是由（２．７）和（２．８）所定义的，则系统（４．４）在有限时间内是精确可控的．证明：由题意知，我们只须验证命题４．１的条件成立即可．我们首先求出Ａ‘的对应于本征值石的本征向量以，由Ａ‘的定义域（３．２）及表达式（３．３），直接计算可得

’ｋ＝（ｅ—Ａｎ王，ｅＡｎ霉，一ｒｅｋｐ。一ｎ，一Ｔｅ—ｋ（ｒ害一ｎ，ｅ—Ａｎ霉，ｅＡｎ霉）Ｔ

以及

…１２＝ｓｉｎｈ撇（２Ｒ／、ｎｅＡｎ）（２＋手１）＋ｒ—ｓｉｎｈ］［２Ｒ丽ｅＡｎ：（＿ｒ－一１）］

又因为＜ｂ，讥＞＝ｅｋ，可得

０＜魈Ｉ＜６，‰＞Ｉ＿ｎｉｎ∈ｚｆｌｅＡ＂Ｉ＜ｓｎｕ∈ｚｐ［＜６，‰＞ｌ＜∞

再利用定理２．３，定理２．４以及定理３．２可知，命题４．１的所有条件都得到了验证，即控制系统（４．４）在有限的时间内是精确可控的．

总结

本文从具有阻尼时滞项的弦系统出发，对时滞系统的半群生成、指数稳定性、Ｒｉｅｓｚ基的存在性及开环系统的精确可控性问题作了系统的研究．具体来说：

一．具有阻尼的系统通过线性变换转化成无阻尼的系统，然后我们又对其做了一系列的处理，得到了系统的抽象方程．最后我们利用等价内积方法及Ｌｕｍｍｅｒ－Ｐｈｉｌｉｐｓ定理证明了算子＾生成一个岛半群，并简单的做了系统算子的谱分析．

二．采用Ｒｉｅｓｚ基方法证明系统的指数稳定性．首先我们证明系统算子Ａ的广义特征向量组的完备性，即构成了空间的Ｒｉｅｓｚ基．后欲证明Ａ的广义本征元系构成饨的一组Ｒｉｅｓｚ基，关键就是在于证明Ａ的谱集具有可分离性，通过前面的谱分析等准备工作，，我们得到了算子Ａ的谱集具有可分离性．

三．通过对开环系统的共轭算子的讨论，得到了共轭算子所对应的本征值的规格化本征元系构成了咒的一组Ｒｉｅｓｚ基，从而得到了开环系统在有限时间内是精确可控的．

本文的弦系统中一些待进一步研究的问题：

在本文中我们只是对通过线性转换后的时滞系统算子做了简单的谱分析，对于算子全面的谱分析并没有研究．另外，对于没有变换前的系统，已经有了精确的算子谱分析，那么通过线性变换后的系统的算子谱结构和原来的算子谱结构是否有着内在的联系，是否就是在平面上差一个平移？这都有待于作进一步的研究．

个人简历

姓名：杨欣性别：男民族：汉

政治面貌：中共党员出生年月：１９８７年２月

２００５年９月．２００９年７月安徽师范大学理学学士

２００９年９月一２０１２年７月郑州大学数学系

在校期间获得奖励及研究项目：

１．郑州大学第六届研究生论文大赛理工类优秀奖．

２．在研项目名称：迁移模型中本质谱及临界谱研究（郑州大学研究生科学研究基金１．

参考文献

【１】１贾军国．弦振动反馈系统的边界控制及相关问题研究【Ｄ】．西安交通大学博士论文，０２３１，２００６，１２－６１．

【２】Ｊ．Ｌ．Ｌｉｏｎｓ．Ｅｘａｃｔｃｏｎｔｒｏｌｌａｂｉｌｉｔｙ，ｓｔａｂｉｌｉｚａｔｉｏｎａｎｄｐｅｒｔｕｒｂａｔｉｏｎｓｆｏｒｄｉｓｔｒｉｂｕｔｅｄｐａｒａｍｅｔｅｒｓｙｓｔｅｍ［Ｊ］．ＳＩＡＭ，１９８８，３０：１－６８．

【３】王康宁，关肇直．弹性震动的镇定问题【Ｊ１．中国科学，１９７４，３（４）：３３５－３５０．

【４】陈翰馥，郭雷．现代控制理论的若干进展及展望【Ｊ】．科学通报，１９９８，４３（１）：１．７．

【５】Ｉ．ＧｕｍｏｗｓｋｉａｎｄＣ．Ｍｉｔａ．ＯｐｔｉｍｉｚａｔｉｏｎｉｎＣｏｎｔｒｏｌＴｈｅｏｒｙａｎｄＰｒａｃｔｉｃｅ［Ｍ］．ＣａｍｂｒｉｄｇｅＵｎｉ－ｖｅｒｓｉｔｙＰｒｅｓｓ，Ｃａｍｂｒｉｄｇｅ，１９６８．

【６】Ｉ．Ｈ．Ｓｕｃｈａｎｄｚ．Ｂｉｅｎ．ＵｓｅｏｆＴｉｍｅｄｅｌａｙａｃｔｉｏｎｉｎｔｈｅｃｏｎｔｒｏｌｌｅｒｄ．ｉｇｎ［Ｊ］．ＩＥＥＥ，Ｔｒａｎｓ．Ａｕｔｏｍａｔ．Ｃｏｎｔｒ０１．１９８０，ＡＣ－２５：６００－６０３．

【７】ＪｕｎｇｕｏＪｉａ，ＭｉａｎｓａｎＷａｎｇ．ＥｘｐｏｎｅｎｔｉａｌＳｔａｂｉｌｉｔｙｏｆａｋｉｎｄｏｆＥｑｕａｔｉｏｎｗｉｔｈＢｏｕｄａｒｙＦｅｅｄｂａｃｋＣｏｎｔｒ０１．ＪｏｕｒｎａｌｏｆＡｐｐｌｉｅｄＭａｔｈｅｍａｔｉｃｓａｎｄＣｏｍｐｕｔｉｎｇ［Ｊ］．２００６，２２（３）：２６７－２７６．ｆ８】贾军国，郭同德．基于波动方程边界反馈控制系统稳定性的谱分析四．郑州大学学报（工学版），２００５，２６（３）：８３－８５．

【９】周鸿兴，王连文．线性算子半群理论及应用【Ｍ】．山东：科学出版社，１９９４．

【１０】Ａ．Ｐａｚｙ．Ｓｅｍｉｇｒｏｕｐｓｏｆｌｉｎｅａｒｏｐｅｒａｔｏｒｓａｎｄａｐｐｌｉｃａｔｉｏｎｓｔｏｐａｒｔｉａｌｄｉｆｆｅｒｅｎｔｉａｌｅｑｕａｔｉｏｎｓ［Ｍ］．

Ｓｐｒｉｎｇ－Ｖｅｒｌａｇ，ＮｅｗＹｏｒｋ，１９８３．

【１１】ｚ．Ｈ．Ｌｕｏ，Ｂ．ｚ．ＧｕｏａｎｄＯ．Ｍｏｒｇｕｌ．ＳｔａｂｉｌｉｔｙａｎｄＳｔａｂｉｌｉｚａｔｉｏｎｏｆＩｎｆｉｎｉｔｅＤｉｍｅｎｓｉｏｎａｌＳｙｓｔｅｍ

ｗｉｔｈＡｐｐｌｉｃａｔｉｏｎｓ［Ｍ］．Ｓｐｒｉｎｇ－ＶｅｒｌａｇＬｏｎｄｏｎＬｉｍｉｔｅｄ，Ｌｏｎｄｏｎ，１９９９．

【１２】张恭庆，林源渠（编著）．泛函分析讲义（上）ｆＭｌ．北京：北京大学出版社，１９８７年３月．

【１３】张恭庆，郭懋正（编著）．泛函分析讲义（下）【Ｍ】．北京：北京大学出版社，１９９０年ｌｏ月．１１４】孙炯，土忠（编著）．线性算子的谱分析【Ｍ１．北京：科学出版社，２００５年９月．３１

【１５］Ｂａｏ－ＺｈｕＧｕｏ，Ｇｅｎ－ＱｉＸｕ．Ｅｘｐａｎｓｉｏｎｏｆｓｏｌｕｔｉｏｎｉｎｔｅｒｍｓｏｆｇｅｎｅｒａｌｉｚｅｄｅｉｇｅｎｆｕｎｃｔｉｏｎｓｆｏｒ

ａｈｙｐｅｒｂｏｌｉｃｓｙｓｔｅｍｗｉｔｈｓｔａｔｉｃｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎ［Ｊ］．ＪｏｕｒｎａｌｏｆＦｕｎｃｔｉｏｎａｌＡｎａｌｙｓｉｓ，２００６，２３１：２４蚴８．

【１６１Ｎ．Ｄｕｎｆｏｒｄ，Ｊ．Ｔ．Ｓｃｈｗａｒｔｚ．ＬｉｎｅａｒＯｐｅｒａｔｏｒｓ，ＰａｒｔＩｎ［Ｍ］．Ｗｉｌｅｙ－Ｉｎｔｅｒｓｃｉｅｎｃｅ，ＮｅｗＹ０ｒｋ．１９７１．

【１７】Ｋ．Ｊ．Ｅｎｇｅｌ，Ｒ．Ｎｅｇｄ．Ｏｎｅ－ＰａｒａｍｅｔｅｒＳｅｍｉｇｒｏｕｐｓｆｏｒＬｉｎｅａｒＥｖｏｌｕｔｉｏｎＥｑｕａｔｉｏｎ［Ｍ］．Ｓｐｒｉｎｇｅｒ－

Ｖｅｒｌａｇ，Ｂｅｒｌｉｎ／ＮｅｗＹｏｒｋ，２０００．

【１８】郭霄，程代展，冯德兴．控制论导论一一从基本概念到研究前沿【Ｍ】．科学技术出版社，

北京，２００５年３月．

【１９】Ｇ．Ｑ．ＸｕａｎｄＢ．Ｚ．Ｇｕｏ．ＲｉｅｓｚｂａｓｉｓｐｒｏｐｅｒｔｙｏｆｅｖｏｌｕｔｉｏｎｅｑｕａｔｉｏｎｓｉｎＨｉｌｂｅｒｔｓｐａｃｅｓａｎｄ

ａｐｐｌｉｃａｔｉｏｎｔｏａｃｏｕｐｌｅｄｓｔｒｉｎｇｅｑｕａｔｉｏｎ［Ｊ］．ＳＩＡＭＪ．ＣｏｎｔｅｏｌａｎｄＯｐｔｉｍ，２００３，４２（３）：９６６－９８４．

【２０］Ｓ．Ａ．ＡｖｄｏｎｉｎａｎｄＳ．Ａ．Ｉｖａｎｏｖ．Ｆａｍｉｌｉｅｓｏｆｅｘｐｏｎｅｎｔｉａｌｓ：Ｔｈｅｍｅｔｈｏｄｏｄｍｏｍｅｎｔｓｉｎｃｏｎｔｒｏｌ－

ｌａｂｉｌｉｔｙｐｒｏｂｌｅｍｓｆｏｒｄｉｓｔｒｉｂｕｔｅｄｐａｒａｘｎｅｔｅｒ８ｙ８ｔｅ脚【Ｍ】．ＣａｍｂｒｉｄｇｅＵｎｉｖｅｒｓｉｔｙＰｒｅｓｓ，ＵＫ，１９９５．

【２１】Ｇ．Ｑ．ＸｕａｎｄＳ．Ｐ．Ｙｕｎｇ．ＴｈｅｅｘｐａｎｓｉｏｎｏｆｓｅｍｉｇｒｏｕｐａｎｄｃｒｉｔｅｒｉｏｎｏｆＲｉｅｓｚｂａ８ｉ８闭．Ｊｏｕｒｎａｌ

ｏｆＤｉｆｆｅｒｅｎｔｉａｌＥｑｕａｔｉｏｎｓ，２００５，２１０：１?２４．

ｆ２２】Ｂ．ＪａｃｏｂａｎｄＨ．Ｚｗａｒｔ．ＥｘａｃｔｃｏｎｔｒｏｌｌａｂｉｌｉｔｙｏｆＣｏ－ｇｒｏｕｐｓｗｉｔｈｏｎｅ－ｄｉｍｅｎｓｉｏｎａｌｉｎｐｕｔｏｐ－

ｅｒａｔｏｒｓ，ｉｎ”ＡｄｖａｎｃｅｓｉｎＭａｔｈｅｍａｔｉｃａｌＳｙｓｔｅｍｓＴｈｅｏｒｙ＂ｅｄｉｔｅｄｂｙＦ．Ｃｏｌｏｎｉｕｓ［Ｊ］．ＳｙｓｔｅｍｓＣｏｎｔｒｏｌＦｏｕｎｄ．Ａｐｐｌ．，Ｂｉｒｋｈ＿ｉｉｕｓｅｒ，Ｂｏｓｔｏｎ，ＭＡ，２０００，２２１－２４２．

【２３】ＪｕｎｇｕｏＪｉａ，ＭｉａｎｓｅｎＷａｎｇ，ＭｅｉｌｉＬｉ．ＰｅｒｉｏｄｉｃＳｏｌｕｔｉｏｎｓｆｏｒＩｍｐｕｌｓｉｖｅＤｅｌａｙＤｉｆｆｅｒｅｎｔｉａｌ

ＥｑｕａｔｉｏｎｓｉｎｔｈｅＣｏｎｔｒｏｌＭｏｄｅｌｏｆＰｌａｎｋｔｏｎＡｌｌｅｌｏｐａｔｈｙ［Ｊ］．ＣｈａｏｓＳｏｌｉｔｉｏｎｓ＆Ｆｒａｃｔａｌｓ，２００７，３２（３）：９６２－９６８．

［２４１ｌＬＤａｔｋｏ．ＮｏｔａｌｌｆｅｅｄｂａｃｋｓｔａｂｉｌｉｚｅｄｈｙｐｅｒｂｏｌｉｃｓｙｓｔｅｍｓａｒｅＲｏｂｕｓｔｗｉｔｈｒｅｓｐｅｃｔｔｏｓｍａｌｌ

ｔｉｍｅｄｅｌａｙｉｎｔｈｅｉｒｆｅｅｄｂａｃｋｓ，ＳＩＡＭＪＣｏｎｔｒｏｌａｎｄＯｐｔｉｍ，【Ｊ】．１９８６，２４：１５２－１５６．

｛２ｓ］Ｊｕｎ－ｇｕｏＪｉａ，Ｓｏｎｇ－ｈｕａＹａｎｇ，Ｍｉａｎ－ｓｅｎＷａｎｇ．ＴｈｅＥｓｔｉｍａｔｉｏｎｏｆＥｘｐｏｎｅｎｔｉａｌＤｅｃａｙａｂｏｕｔ

ａＫｉｎｄｏｆＷａｖｅＥｑｕａｔｉｏｎｗｉｔｈＢｏｕｎｄａｒｙＦｅｅｄｂａｃｋＣｏｎｔｒｏｌ［ｃ］．ＰｒｏｃｅｅｄｉｎｇｏｆＩＥＥＥ２００６ＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅｏｆＩｎｎｏｖａｔｉｖｅＣｏｍｐｕｔｉｎｇａｎｄＩｎｆｏｒｍａｔｉｏｎＣｏｎｔｒｏｌ，２００６，２：５８７－５９０．３２

【２６］ＰｉｏｔｒＧｒａｂｏｗｓｋｉ．Ｓｐｅｃｔｒａｌａｐｐｒｏａｃｈｔｏｗｅｌｌ—ｐｏｓｅｄｎｅｓｓａｎｄｓｔａｂｉｌｉｔｙａｎａｌｙｓｉｓｏｆｈｙｂｒｉｄｆｅｅｄ－

ｂａｃｋｓｙｓｔｅｍｓ，＆Ｍａｔｈ．Ｓｙｓ．ＥｓｔｉｍａｔｉｏｎａｎｄＣｏｎｔｒｏｌ［Ｊ－］．１９９６，６（１）：ｌ－４０．

【２７１Ｇｅｎ－ｑｉＸｕ，Ｊｕｎ－ｇｕｏＪｉａ．ＴｈｅｇｒｏｕｐａｎｄＲｉｅｓｚｂａｓｉｓｐｒｏｐｅｒｔｉｅｓｏｆｓｔｒｉｎｇｓｙｓｔｅｍｓｗｉｔｈｔｉｍｅ

ｄｅｌａｙａｎｄｅｘａｃｔｃｏｎｔｒｏｌｌａｂｉｌｉｔｙｗｉｔｈｂｏｕｎｄａｒｙｃｏｎｔｒｏｌ［Ｊ］．２００６，２３（１）：８５－９６．

【２８】ＪｕｎｇｕｏＪｉａ，ＭｉａｎｓｅｎＷａｎｇ，ＳｏｎｇｈｕａＹａｎｇ．ＳｏｍｅＲｅｓｕｌｔｓｉｎＴｉｍｅＯｐｔｉｍａｌＴｒａｃｉｎｇＣｏｎｔｒｏｌ

ＰｒｏｂｌｅｍｏｆＮｏｎ－ａｕｔｏｎｏｍｏｕｓＲｅｌａｘｅｄＳｙｓｔｅｍｗｉｔｈＮｏｎｌｉｎｅａｒＣｏｎｔｒｏｌＶａｒｉａｂｌｅｓ［Ｊ］．ＡｐｐｌｉｅｄＭａｔｈｅｍａｔｉｃｓ，２００７，２０（１）：２４－３０．

【２９】王耀庭，王光，李胜家．Ｅｍ盼Ｂ锄ｏｌｌｌｌｉ梁边界反馈控制系统的Ｒｉｅｓｚ基生成问题ｆＪ】．数

学学报，２０００，４３（６）：１０８９－１０９８．

【３０］Ｇ．Ｑ．ＸｕａｎｄＳ．Ｐ．Ｙｕｎｇ．ＥｘｐｏｎｅｎｔｉａｌＤｅｃａｙＲａｔｅｆｏｒａＴｉｍｏｓｈｅｎｋｏＢｅａｍｗｉｔｈＢｏｕｎｄａｒｙ

Ｄａｍｐｉｎｇ［Ｊ］．ＪｏｕｍａｌｏｆＯｐｔｉｍｉｚａｔｉｏｎＴｈｅｏｒｙａｎｄＡｐｐｌｉｃａｔｉｏｎｓ，２００４，１２３（３）：６６９－６９３．［３１１Ｊｕｎ－ｍｉｎＷａｎｇ，Ｇｅｎ－ＱｉＸｕ，Ｓｉｕ－ＰａｎｇＹｕｎｇ．ＥｘｐｏｎｅｎｔｉａｌＳｔａｂｉｌｉｚａｔｉｏｎｏｆＬａｍｉｎａｔｅｄＢｅａｍｓ

ｗｉｔｈＳｔｒｕｃｔｕｒａｌＤａｍｐｉｎｇａｎｄＢｏｕｎｄａｒｙＦｅｅｄｂａｃｋＣｏｎｔｒｏｌｓ［Ｊ］．ＳｉａｍＪ．ＣｏｎｔｒｏｌＯｐｔｉｍ．Ｓｏｃｉ－ｅｔｙｆｏｒＩｎｄｕｓｔｒｉａｌａｎｄＡｐｐｌｉｅｄＭａｔｈｅｍａｔｉｃｓ，２００５，４４（５）：１５７５－１５９７．

【３２］Ｇ．Ｗｅｉｓｓ．Ａｄｍｉｓｓｉｂｉｌｉｔｙｏｆｕｎｂｏｕｎｄｅｄｃｏｎｔｒｏｌｏｐｅｒａｔｏｒｓ，ＳＩＡＭＪ．ＣｏｎｔｒｏｌＯｐｔｉｍ．Ⅲ，１９８９，

２７：５２７－５４５．

【３３】Ｂ．Ｚ．ＧｕｏａｎｄＧ．Ｘ．Ｘｕ．ＲｉｅｓｚｂａｓｉｓａｎｄＥｘｔｒａｃｔｃｏｎｔｒｏｌｌａｂｉｌｉｔｙｏｆＣｏ—ｇｒｏｕｐｗｉｔｈｏｎｅｄｉｍｅｎ－

ｓｉｏｎａｌｉｎｐｕｔｏｐｅｒａｔｏｒｓ，ＳｙｓｔｅｍａｎｄＣｏｎｔｒｏｌＬｅｔｔｅｒｓ［Ｊ］，２００４，５２：２２１?２３２．

致谢

在本篇论文的写作过程中，一直得到导师贾军国教授悉心的指导和帮助，其中凝聚着导师大量的心血，在此向他致以最诚挚的谢意．

回首三年的研究生学习生涯，不管是在学习上还是在生活上，贾老师都给予了我很大的帮助．在学习上，贾老师让我学会了，在学习和研究中要有严谨的态度，要注重对细节的把握．更使我明白了做学问一定不能马虎，不能三心二意，要沉下心深入到你的研究中，要持之以恒，即使在你没有任何想法的时候也要坚持，在积累中你终会做出自己的东西．同样的，贾老师也给十分关心我们的个人生活，不但教诲我们生活中的哲理，而且当我们遇到生活中的挫折和难题时，贾老师语重心长的话语、丰富的人生阅历和经验，对我们走出困境起到了很大的帮助．在此，再一次深深的感谢贾老师三年来的爱护和关心．?

同样，我还要深深地感谢曹策问教授，Ｉ－春霞教授，王长群教授，戚仕硕教授，王秀梅副教授在学习上给予我的无私指导与关怀．他们渊博的知识，敏锐的洞察能力令人钦佩．感谢他们开设的专业课程，通过这些课程的学习，使我拓宽了知识面，开阔了视野，为今后的进一步学习打下了坚实的基础．

感谢三年来一起学习、生活过的室友和同学，向在学习和生活上给予我诸多帮助的师长、同窗、亲人和朋友致以诚挚的谢意．

深深的感谢我的父母对我的教导、鼓励和支持，正是有了他们无私的爱和关怀，才更坚定了我前进的方向．

最后，本文在写作过程中，参阅了国内外专家学者们的相关论著，并吸纳了他们的一些研究理论，在此一并表示感谢！