求数列极限的方法总结
数学科学学院数学与应用数学08级汉班 **
指导教师 ****
摘 要 数列极限的求法一直是数列中一个比较重要的问题,本文通过归纳和总结,从不同的方面罗列了它的几种求法。
关键词 数列极限、定义、泰勒公式、无穷小量
极限一直是数学分析中的一个重点内容,而对数列极限的求法可谓是多种多样,通过归纳和总结,我们罗列出一些常用的求法。求数列极限的最基本的方法还是利用数列极限的定义,也要注意运用两个重要极限,其中,可以利用等量代换,展开、约分,三角代换等方法化成比较好求的数列,也可以利用数列极限的四则运算法则计算。夹逼性定理和单调有界原理是很重要的定理,在求的时候要重点注意运用。泰勒公式、洛必达法则、黎曼引理是针对某些特殊的数列而言的。还有一些比较常用的方法,在本文中都一一列举了。
1.定义法
利用数列极限的定义求出数列的极限.设﹛Xn﹜是一个数列,a是实数,如果对任意给定的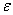 〉0,总存在一个正整数N,当n〉N时,都有
〉0,总存在一个正整数N,当n〉N时,都有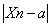 <
<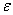 ,我们就称a是数列{Xn}的极限.记为
,我们就称a是数列{Xn}的极限.记为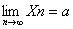 .
.
例1: 按定义证明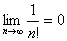 .
.
解:1/n!=1/n(n-1)(n-2)…1≤1/n
令1/n<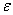 ,则让n>
,则让n>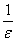 即可,
即可,
存在N=[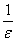 ],当n>N时,不等式:1/n!=1/n(n-1)(n-2)…1≤1/n<
],当n>N时,不等式:1/n!=1/n(n-1)(n-2)…1≤1/n<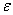 成立,
成立,
所以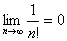 .
.
2.利用极限四则运算法则
对和、差、积、商形式的函数求极限,自然会想到极限四则运算法则.
例2: 求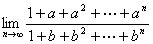 ,其中
,其中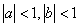 .
.
解: 分子分母均为无穷多项的和,应分别求和,再用四则运算法则求极限
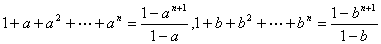 ,
,
原式=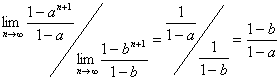 ,
,
3. 利用夹逼性定理求极限
若存在正整数N,当n>N时,有Xn≤Yn≤Zn,且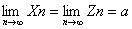 ,则有
,则有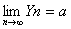 .
.
例3:求{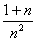 }的极限.
}的极限.
解: 对任意正整数n,显然有
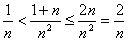 ,
,
而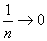 ,
,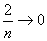 ,由夹逼性定理得
,由夹逼性定理得
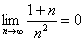 .
.
4.换元法
通过换元将复杂的极限化为简单.
例4.求极限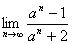 ,此时
,此时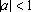
解:若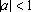 有
有 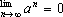 ,令
,令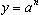 则
则
5.单调有界原理
例5.证明数列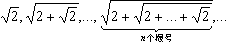 有极限,并求其极限。
有极限,并求其极限。
证: 令 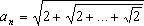 ,易知{
,易知{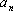 }递增,且
}递增,且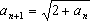
我们用归纳法证明 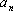 ≤2. 显然
≤2. 显然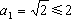 。
。
若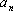 ≤2 则
≤2 则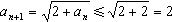 。
。
故由单调有界原理{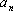 }收敛,设
}收敛,设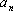 →
→ ,则在
,则在 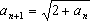 中两边取极限得
中两边取极限得 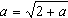 即
即 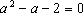
解之得  =2 或
=2 或  =-1 明显不合要求,舍去,
=-1 明显不合要求,舍去,
从而 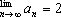
6.先用数学归纳法,再求极限.
例6:求极限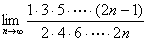
解: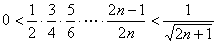
S=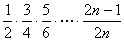
设 =
=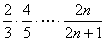 则有S<
则有S<
S2=S*S<S* =
=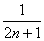
而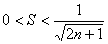 ,
,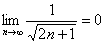 再由夹逼性定理,得
再由夹逼性定理,得
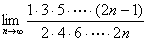 =0
=0
7.利用两个重要极限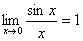 ,
, .
.
例7:求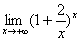
解: 原式=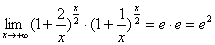
8.利用等价无穷小来求极限
将数列化成自己熟悉的等价无穷小的形式然后求极限.
例8:求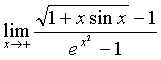
解:当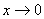 的时候,
的时候, ,
, .
.
而此时, ,所以
,所以
原式=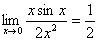
9.用洛必达法则求极限.适用于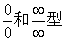
例9:求
解: 是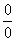 待定型.
待定型.
 =
=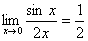
10.积分的定义及性质
例10:求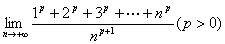
解: 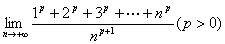 =
=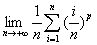
设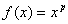 ,则
,则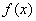 在[0,1]内连续,
在[0,1]内连续,
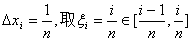
所以, 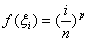
所以原式=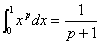
11.级数收敛的必要条件.
设 据必要条件知所求表达式的极限为0.
据必要条件知所求表达式的极限为0.
例11:求
解:设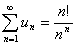 ,则
,则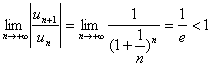
所以该级数收敛,所以 =0
=0
12.对表达式进行展开、合并、约分和因式分解以及分子分母有理化,三角函数的恒等变形。
例12. 求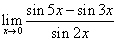
解:
法一:原式=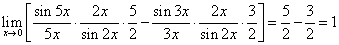
法二:原式=
13.奇数列和偶数列的极限相同,则数列的极限就是这个极限。
例13:求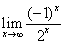 的值
的值
解:奇数列为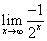 =0
=0
偶数列为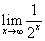 =0
=0
所以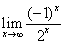 =0
=0
14.利于泰勒展开式求极限。
例14.求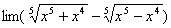
解:原式=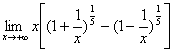 (令t=
(令t=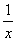 )
)
=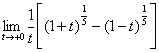 =
=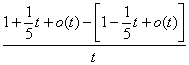 =
=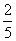
15.利于无穷小量的性质和无穷小量和无穷大量之间的关系求极限。
利用无穷小量与有界变量的乘积仍为无穷小量,无穷小量与无穷大量互为倒数的关系,以及有限个无穷小的和仍是无穷小等等。
例15:求 的值
的值
解:因为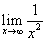 是无穷小量,而
是无穷小量,而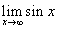 是有界变量,所以
是有界变量,所以
 还是无穷小量,即
还是无穷小量,即
 =0
=0
16.利用数列的几何、算术平均值求极限。
数列{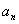 }有极限,则它的几何平均值和算术平均值的极限与与原极限相同。
}有极限,则它的几何平均值和算术平均值的极限与与原极限相同。
例16:求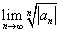 的值
的值
解: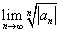 =
=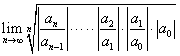 =
=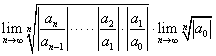
设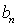 =
=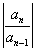 ,因为知
,因为知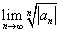 =1
=1
所以,所求原式的极限就等于{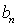 }的极限
}的极限
即原式=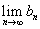 =
=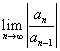
17.绝对值中的极限
若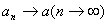 ,则
,则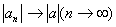
例17:求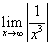 的值
的值
解: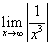 =
=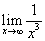 =0
=0
18.利用黎曼引理
例18:求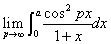 (a>0)
(a>0)
解:原式=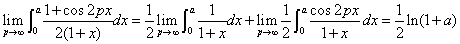
数列极限的方法还有很多,以上给与大致列举。本文在写作过程中得到了****老师多次精心指导,在此表示感谢。
参考文献
1. 欧阳光中、朱学炎、金福临等,数学分析第三版上册,高等教育出版社,1978年
第二篇:数学学年论文毕业论文求极限的方法
求极限的方法
摘 要:本文系统地介绍了利用两个重要极限、无穷小量代换、洛比达法则、泰勒公式、定积分等求极限的方法,并结合具体的例子,指出了在解题过程中常遇见的一些问题。
关键词:极限、方法、类型、洛比达法则、定积分
一 引言
高等数学是以函数为研究对象,以极限理论和极限方法为基本方法,以微积分学为主要内容的一门学科,极限理论和极限方法在这门课程中占有极其重要的地位。高等数学许多深层次的理论及其应用都是极限的延拓和深化,如连续、导数、微积分等等都是由极限定义的,离开了极限的思想高等数学就失去了基础失去了价值,因此极限运算是高等数学的基本运算。由于极限定义的高度抽象使我们很难用极限定义本身去求极限,又由于极限运算分布于整个高等数学的始终,许多重要的概念是由极限定义的。极限知识是研究导数、各种积分、级数等的基本工具。反过来,我们也可以利用这些概念来求一些极限,所以运算方法繁多。针对这种情况,本文作者通过立体归纳总结出了如下常见的求极限的方法。
二 具体方法
⒈利用函数极限的四则运算法则来求极限
定理1①:若极限limf(x)和limg(x)都存在,则函数f(x)?g(x),f(x)?g(x)
x?x0x?x
当x?x0时也存在且
①lim?f(x)?g(x)??
x?0limx?x0
x?x0f(x)?limx?x.0g(x) ②lim?f(x)?g(x)??x?x0limf(x)?limg(x) x?x0
又若limg(x)?0,则
x?x0f(x)g(x)在x?x0时也存在,且有
limx?x0f(x)g(x)lim?x?x0f(x)g(x)lim
x?x0
利用极限的四则运算法则求极限,条件是每项或每个因子极限存在,一般所 1
给的变量都不满足这个条件,如??、00等情况,都不能直接用四则运算法则,
必须要对变量进行变形,设法消去分子、分母中的零因子,在变形时,要熟练掌握饮因式分解、有理化运算等恒等变形。
例1:求limx2?4
x?2?x?2
解:原式=lim?x?2??x?2?
x?2?x?2?lim?x?2??0
x?2?
⒉用两个重要的极限来求函数的极限 ①利用limsinx?1来求极限
x?0x
limsinx
x?0x?1的扩展形为:
令g?x??0,当x?x0或x??时,则有
limsing?x?sing?x?
x?x0g?x??1或limx??g?x??1
例2:limsinx
x????x
解:令t=??x.则sinx=sin(?? t)=sint, 且当x??时t?0 故 limsinx
x????x?limsint
t?0t?1
例3:求limsin?x2?1?
x?1x?1
解:原式=lim?x?1??sin?x2?1??2
?
x?1?x?1??x?1?lim?x?1??sin?x?1??
x?1x2?12 ②利用lim(1?1)?e来求极限
x??x
1
lim(1?1)?e的另一种形式为
x??xlim(1??)??e.事实上,
??0
2 令
??1
x.x?????0.所以e?limx??(1?1x1)?xlim??0(1??)??e
1
例4: 求lim(1?2x)x的极限
x?0
解:原式=limx?011??22x2x?(1?2x)?(1?2x)??e ??
利用这两个重要极限来求函数的极限时要仔细观察所给的函数形式只有形式符合或经过变化符合这两个重要极限的形式时才能够运用此方法来求极限。一般常用的方法是换元法和配指数法。
⒊利用等价无穷小量代换来求极限 所谓等价无穷小量即limx?x0f(x)g(x)?1.称f(x)与g(x)是x?x0时的等价无穷
小量,记作f(x)~g(x).(x?x0).
定理2②:设函数f(x),g(x),h(x)在u0(x0)内有定义,
且有f(x)~g(x).(x?x0)
① 若limf(x)g(x)?A,则limg(x)h(x)?A
x?x0x?x0
② 若limx?x0h(x)f(x)?B,则limx?x0h(x)g(x)?B 证明:①limg(x)h(x)?
x?x0limx?x0g(x)f(x)?limf(x)h(x)?1?A?A x?x0
②可类似证明,在此就不在详细证明了!
由该定理就可利用等价无穷小量代换来求某些函数的极限
例5:求limx?0tanx?sinxsinx3的极限
(1?cosx).而sinx~x,(x?0); 解:由 tanx?sinx?
1?cosx~x2sinxcosx
2,(x?0);nis33x?x~x,(x?0).
3
故有limx?0tanx?sinxsinx3= lim
x?01cosxx??x2?1 32x
注:由上例可以看出,欲利用此方法求函数的极限必须熟练掌握一些常用的 等价无穷小量,如:由于
arctaxn
xlimx?0sinxx?1,故有sinx~x,(x?0).又由于limx?0?1,故有arctanx~x,(x?0).
另注:在利用等价无穷小代换求极限时,应该注意:只有对所求极限中相乘或相除的因式才能用等价无穷小量来代换,而对极限式中的相加或相减的部分则不能随意代换。如上式中,若因有tanx~x,(x?0);sinx~x,(x?0).而推出 limx?0tanx?sinxsinx3=lim
x?0x?xsinx3?0 则得到的结果是错误的。
⒋ 利迫敛性来求极限
定理3③:设limf(x)= limg(x)=A,且在某uo(x0,?')内有f(x)?h(x)?g(x),
x?x0x?x0
则limh(x)=A
x?x0
例6:求limx??的极限
?x?x?0??1?
解:?1?x??<1-x. 且lim(1?x)?1 由迫敛性知
?x?x?0??1?
?limx?0?x??=1 ?x??1?
做此类型题目的关键在于找出大于已知函数的函数和小于已知函数的函数,并且所找出的两个函数必须要收敛于同一个极限。
⒌利用函数的连续性求极限
利用函数的连续性求极限包括:如函数f(x)在x0点连续,则
limf(x)?
x?x0f(x0)及若lim?(x)?a x?x0
且f(u)在点a连续,则
4
limx?x0??f??(x)??f?lim?(x)? ?x?x0?
1?cosx
x2例7:求lime2arcsin
x?0的极限
1
414解:由于
1?coxslim2arx?0
21?coxscsxin122?及函数f?u??e4在u?处连续,故lime2a
x?0rcxsin=elim1?cosx2arcsinxx?0=e4。
⒍利用洛比达法则求函数的极限
在前面的叙述中,我们已经提到了利用等价无穷小量来求函数的极限,在此笔者叙述一种牵涉到无穷小(大)量的比较的求极限的方法。我们把两个无穷小量或两个无穷大量的比的极限统称为不定式极限,分别记作00型或??型的不定
式极限。现在我们将以导数为工具研究不定式极限,这个方法通常称为洛比达法则。
下面就给出不定式极限的求法。
(1)对于0
0型不定式极限,可根据以下定理来求出函数的极限
定理4④:若函数f(x)和函数g(x)满足:
①limf(x)=limg(x)=0。
x?x0x?x0
②在点x0的某空心邻域u0(x0)内两者都可导,且g'(x)?0
③limx?x0f'(x)g'(x)=A。(A可为实数,也可为??或?)
f'(x)
g'(x)则limx?x0f(x)g(x)=limx?x0=A。
注:此定理的证明可利用柯西中值定理,在此,笔者就不一一赘述了。 例8:求limx??1?cosxtan2x
解:容易检验
f(x)=1+cosx与g(x)=tan2x在x0??的邻域里满足定理的条件①和②,又因
5
lim?
x?
f'(x)g'(x)
=lim
x??
?sinx2tanxsec
2
x
= -lim
x??
cosx2
3
?
12
故由洛比达法则求得,
lim
x?x0
f(x)g(x)
=lim
x?x0
f'(x)g'(x)
=
12
00
在此类题目中,如果lim
x?x0
f'(x)g'(x)
仍是型的不定式极限,只要有可能,我们
f'(x)g'(x)
可再次利用洛比达法则,即考察极限lim
x?x0
是否存在。当然,这是f'(x)和
g'(x)在x0的某邻域内必须满足上述定理的条件。
1
例9:求
lim
x?0
e?(1?2x)2
ln(1?x)
2
x
解:利用ln(1?x2)~x2 (x?0),则得
1
原式=lim
x?0
e?(1?2x)2
x
2
x
=lim
x?0
e?(1?2x)
2x
x
?
12
=lim
x?0
e?(1?2x)
2
x
?
32
?
22
?1
在利用洛比达法则求极限时,为使计算更加快捷减少运算中的诸多不便,可用适当的代换,如下例, 例10:求lim
x?0
?
x1?e
x
解:这是
00
型不定式极限,可直接运用洛比达法则求解,但是比较麻烦。如作适
当的变换,计算上就会更方便些,故 令t?
x,当x?0
?
时有t?0?,于是有
x
lim
x?0
?
1?e
x
=lim
t?0
?
t1?e
t
?
lim
t?0
?
1?e
t
??1
(2)
??
型不定式极限
若满足如下定理的条件,即可由如下定理计算出其极限。 定理5⑤:若函数f(x)和函数g(x)满足:
6
①limf(x)=limg(x)=?
x?x0?x?x0?
②在点x0的某空心邻域u0?(x0)内两者都可导,且g'(x)?0
③limx?x0f'(x)g'(x)
f(x)
g(x)=A,(A可为实数,也可为??或?)。 f'(x)g'(x)?则limx?x0?=limx?x0=A。 ?
此定理可用柯西中值定理来证明,在此,笔者就不一一赘述了。 例11:求limx???lnxx
解:由定理4得,
limx???lnxx?limx???(lnx)(x)''?lim
x???lx?0
注1:若limx?x0f'(x)g'(x)不存在,并不能说明limx?x0f(x)g(x)不存在。
注2:不能对任何比式极限都按洛比达法则来求解。首先必须注意它是不是不定式极限;其次是观察它是否满足洛比达法则的其它条件。
下面这个简单的极限
limx??x?sinxx=1 虽然是?
?型的,但若不顾条件随便使用洛比达法则:
x?sinx
xlimx??=limx??1?cosx1就会因右式的极限不存在而推出原式的极限
不存在这个错误的结论。
(3)其它类型不定式极限
不定式极限还有0??,1?,00,?0,???等类型。这些类型经过简单的变换,都可以化为型和00??型的不定式极限。
例12:求limxlnx
x?0?
7
解:这是一个1?型的不定式极限,作恒等变形xlnx=
lnx1x
,将它转化为
??
型的
不定式极限,并用洛比达法则得到
1
lnx1x
1
lim
x?0
?
xlnx
=lim
x?0
?
=lim
x?0
?
x=(?x)?0 ?1lim?
x?0x
2
例13:求lim(cosx)x
x?0
2
解:这是一个1?型的不定式极限,作恒等变形
1
1
(cosx)
x
2
=e
x
2
lncosx
00
其指数部分的极限
1
2
lim
x?0
1x
2
lncosx
是
12
1
型的不定式极限,可先求得
limx
x?0
lncosx
=lim
x?0
?tanx2x
=?
12
从而得lim(cosx)x=e
x?0
2
?
k
例14: 求lim(sinx)1?lnx(k为常数)
x?0
?
解:这是一个00型的不定式极限,按上例变形的方法,先求
kcosx
klnsinx1?lnx
xsinx
=limkcosx?=k 1?sinxx?0
??
型的极限,
lim
x?0
?
?
lim
x?0
?
x
k
然后得到 lim(sinx)1?lnx=ek(k?0)
x?0
?
当k=0时上面的结果仍成立。
1
例15: 求lim(x??x)lnx
x???
2
8
解:这是一个?0型的不定式极限,类似地,先求其对数的极限(
1
??
型)
lim
ln(x??x)
2
x???
lnx
=lim
x???
?x1x
=1
1
于是有lim(x?1?x)lnx=e
x???
2
⒎利用泰勒公式求极限
由于泰勒公式的特殊形式,对于求解某些函数的极限有简化求解过程的作用。 例16:求lim
x?0
cosx?e
x
4
?
x
2
2
解:本题可用洛比达法则来求解,但是运算过程比较繁琐,在这里可用泰勒公式求解,考虑到极限式的分母为x4,我们用麦克劳林公式表示极限的分子, (取n=4) cosx=1-x
2
x
2
2x
2
+
x
4
24x
4
+o(x5)
e
?
2
=1-
2
x
2
+
8x
4
?o(x)
5
cosx-e
?
2
=-
12
?o(x)
5
因而求得lim
x?0
cosx?e
x
4
?
x
2
2
?
1x?o(x)x
4
45
=lim
x?0
??
112
⒏利用微分中值定理和积分中值定理求极限
例17:求
x
lim
x?0
2?2
x
3
xsinx
的极限
x
sinx
解:?
2?2
x
3
sinx
?
2?2
x?sinx
?
x?sinxx
3
由微分中值定理得,
9
2?2
xsinx
x?sinx
?2ln2
?
(?介于x与sinx之间)
?
原式=lim
x?0
2?2
xsinx
x?sinx
x
?lim
x?0sinx
x?sinxx
3
lim?2
??0
?
ln2?lim
x?0
?
1?cosx3x
2
?
ln26
例18:求
x
lim
x?0
2?2
x
3
的极限
x
sinx
解:?
2?2
x
3
sinx
?
2?2
x?sinx
?
x?sinxx
3
由微分中值定理得,
2?2
x
sinx
x?sinx
?2ln2
?
(?介于x与sinx之间)
?lim
x?0
原式=lim
x?0
2?2
xsinx
x?sinxx
3
x?sinx
?
lim?2
??0
?
ln2?lim
x?0
?
1?cosx3x
2
?
ln26
⒐利用定积分求极限
例19:求
lim
n??
(
1n?1
?
1n?2
??
1
2n
)
解:把此极限式化为某个积分和的极限式,并转化为计算计算定积分,为此作如下变形:
n
J?
lim?
n??
11?
in
?
1n
i?1
不难看出,其中的和式是函数发f(x)?里所取的是等分分割,?xi?
J?
1n
1
11?x
在区间?0,1?上的一个积分和。(这(i?1.2.??????n.), 所以
, ?i?
?i?1i?
??,n?nn??
i
?
1
dx1?x
?ln(1?x)?
?ln2
当然,也可把J看作f(x)?
J?
1x
在?1,2?上的定积分,同样有
?
2
dxx
1
?
?
3
dxx?1
2
????????ln2
三 总结
10
以上方法是在高等数学里求解极限的重要方法。在做求解极限的题目时,仅仅掌握以上方法的而不能够透彻清晰地明白以上各方法所需的条件也是不够的,必须要细心分析仔细甄选,选择出适当的方法。这样不仅准确率更高,而且会省去许多不必要的麻烦,起到事半功倍的效果。这就要求学习者要吃透其精髓,明了其道理,体会出做题的窍门。达到这样的境界非一日之功,必须要多做题善于总结,日积月累,定会熟能生巧,在做题时得心应手。
注释:①②③④⑤,华东师范大学数学系,《数学分析》,高等教育出版社,20xx年6月第3版,第49,62,49,127,128页。
参考文献
① 华东师范大学数学系,《数学分析》,高等教育出版社,20xx年6月第3版 ② 陈传璋,朱学炎等,《数学分析》,复旦大学数学系,高等教育出版社 ③ 郝涌,卢士堂等,《数学考研精解》,华中理工大学出版社
The Methods of Asking Limits
Abstract: The paper represents systematically the methods of asking the limits by using the two important limits, the infinitesimal quantities substitution, L’Hospital rule, Taylor formula and the definite integral, etc. And the author also points out some problems in the course of asking the answers, combining with the specific examples.
Key word: Limit, Methods, Patterns, L’Hospital rule, Definire integral
11
