导数知识点归纳及应用
●知识点归纳
一、相关概念
1.导数的概念
函数y=f(x),如果自变量x在x0处有增量?x,那么函数y相应地有增量?y=f(x0+?x)-f(x0),比值
之间的平均变化率,即?y叫做函数y=f(x)在x0到x0+?x?x?yf(x0??x)?f(x0)?y=。如果当?x?0时,有?x?x?x极限,我们就说函数y=f(x)在点x0处可导,并把这个极限叫做f(x)在点x0处的导数,记作f’(x0)或y’|x?x。 0
lim即f(x0)=?x?0f(x0??x)?f(x0)?ylim=?。 ?xx?0?x
注意:
(1)函数f(x)在点x0处可导,是指?x?0?y?y有极限。如果?x?x不存在极限,就说函数在点x0处不可导,或说无导数。
(2)?x是自变量x在x0处的改变量,?x?0时,而?y是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x0处的导数的步骤: ① 求函数的增量?y=f(x0+?x)-f(x0); ② 求平均变化率?yf(x0??x)?f(x0)=; ?x?x
lim③ 取极限,得导数f’(x0)=?x?0?y。 ?x
例:设f(x)= x|x|, 则f′( 0)= .
lim[解析]:∵?x?0f(0??x)?f(0)f(?x)|?x|?x?lim?lim?lim|?x|?0 ?x?0?x?0?x?0?x?x?x
∴f′( 0)=0
2.导数的几何意义
函数y=f(x)在点x0处的导数的几何意义是曲线y=f(x)在点p(x0,f(x0))处的切线的斜率。也就是说,曲线y=f(x)在点p(x0,f(x0))处的切线的斜率是f’(x0)。
相应地,切线方程为y-y0=f/(x0)(x-x0)。
例:在函数y?x3?8x的图象上,其切线的倾斜角小于的点中,坐标
为整数的点的个数是
A.3 B.2 C.1 D.0 ( ) ?4
[解析]:切线的斜率为k?y/?3x2?8 又切线的倾斜角小于,即0?k?1
故0?3x2?8?1 解得:?3?x??88?x?3 33?4
故没有坐标为整数的点
3.导数的物理意义
?t)若物体运动的规律是s=s(t),那么该物体在时刻t的瞬间速度v=s(。
若物体运动的速度随时间的变化的规律是v=v(t),则该物体在时刻t的加速度a=v′(t)。
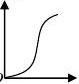
例:汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把
这一过程中汽车的行驶路程s看作时间t的函数,其图像可能是( )
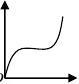
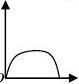
A.
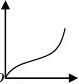
B. C. D. 答:A。
练习:已知质点M按规律s?2t2?3做直线运动(位移单位:单位:s)。
(1) 当t=2,?t?0.01时,求?s
?t;
(2) 当t=2,?t?0.001时,求?s
?t;
(3) 求质点M在t=2时的瞬时速度。 答案:(1)8.02(2)8.002;(3)8
二、导数的运算
1.基本函数的导数公式:
①C??0;(C为常数)
②?xn???nxn?1;
③(sinx)??cosx;
④(cosx)???sinx;
⑤(ex)??ex;
⑥(ax)??axlna;
⑦?lnx???1
x;
⑧?log1
ax???xlogae.
例1:下列求导运算正确cm,时间的是
( )
A.(x+)??1?1
x11 B.(logx)′= 22xln2x
C.(3x)′=3xlog3e D. (x2cosx)′=-2xsinx
[解析]:A错,∵(x+)??1?1
x1 x2
1 xln2 B正确,∵(log2x)′=
C错,∵(3x)′=3xln3
D错,∵(x2cosx)′=2xcosx+ x2(-sinx)
例2:设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)=
( )
A.sinx B.-sinx C
D.-cosx
[解析]:f0(x) = sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)= -sinx, .cosx
f3(x)=f2′(x)= -cosx, f4(x) = f3′(x)=sinx,循环了
则f2005(x)=f1(x)=cosx
2.导数的运算法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即: (u?v)'?u'?v'.
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即:(uv)'?u'v?uv'.
若C为常数,则(Cu)'?C'u?Cu'?0?Cu'?Cu'.即常数与函数的积的导数等于常数乘以函数的导数: (Cu)'?Cu'.
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分?u'v?uv'?u?母的导数与分子的积,再除以分母的平方:???(v?0)。 v2?v?
例:设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f?(x)g(x)?f(x)g?(x)>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A. (-3,0)∪(3,+∞) B. (-3,0)∪(0, 3)
C. (-∞,- 3)∪(3,+∞) D. (-∞,- 3)∪(0, 3)
[解析]:∵当x<0时,f?(x)g(x)?f(x)g?(x)>0 ,即[f(x)g(x)]/?0
∴当x<0时,f(x)g(x)为增函数,
又g(x)是偶函数且g(3)=0,∴g(-3)=0,∴f(-3)g(-3)=0 故当x??3时,f(x)g(x)<0,又f(x)g(x)是奇函数,
当x>0时,f(x)g(x)为减函数,且f(3)g(3)=0
故当0?x?3时,f(x)g(x)<0
故选D
3.复合函数的导数
形如y=f??(x)?的函数称为复合函数。复合函数求导步骤: 分解——>求导——>回代。
法则:y'|X= y'|U ·u'|X或者f?[?(x)]?f?(?)*??(x). 练习:求下列各函数的导数:
(1)y?x?x5?sinx
x2
2?; (2)y?(x?1)(x?2)(x?3); 11?x?1
1?x. x? (3)y??sinx??1?2cos2?; (4)y?4?
1
x2解:(1)∵y?
∴y′?(x??x5?sinxx2?x?32?x3?sinxx25, 3
2)??(x3)??(x?2sin3?x)???x2?3x2?2x?3sinx?x?2cosx. 2
(2) y=(x2+3x+2)(x+3)=x3+6x2+11x+6,∴y′=3x2+12x+11.
x?1(3)∵y=?sinx???cos??sinx, 2?2?2
?1?1?1y???sinx??(sinx)??cosx. 2?2?2
1
1?x?1
1?x?1?x?1?x
(1?x)(1?x)?2
1?x∴(4)y?
∴
, ?2?2??2(1?x)?y????. ??(1?x)2(1?x)2?1?x?
三、导数的应用
1.函数的单调性与导数
(1)设函数y?f(x)在某个区间(a,b)可导,如果f'(x)?0,则f(x)在此区间上为增函数;如果f'(x)?0,则f(x)在此区间上为减函数。
(2)如果在某区间内恒有f'(x)?0,则f(x)为常数。
例:函数f(x)?x3?3x2?1是减函数的区间为 ( )
A.(2,??) B.(??,2) C.(??,0) D.(0,2)
[解析]:由f/(x)?3x2?6x<0,得0<x<2
∴函数f(x)?x3?3x2?1是减函数的区间为(0,2)
2.极点与极值:
曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
例:函数f(x)?x3?ax2?3x?9,已知f(x)在x??3时取得极值,则a=
( )
A.2 B.3 C.4 D.5
[解析]:∵f/(x)?3x2?2ax?3,又f(x)在x??3时取得极值
∴f/(?3)?30?6a?0
则a=5
3.最值:
在区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值。但在开区间(a,b)内连续函数f(x)不一定有最大值,例如f(x)?x3,x?(?1,1)。
(1)函数的最大值和最小值是一个整体性的概念,最大值必须是整个区间上所有函数值中的最大值,最小值必须在整个区间上所有函数值中的最小值。
(2)函数的最大值、最小值是比较整个定义区间的函数值得出来的,函数的极值是比较极值点附件的函数值得出来的。函数的极值可以有多有少,但最值只有一个,极值只能在区间内取得,最值则可以在端点取得,有极值的未必有最值,有最值的未必有极值,极值可能成为
最值,最值只要不在端点处必定是极值。 例:函数f(x)?x3?3x?1在闭区间[-3,0]上的最大值、最小值分别是[解析]:由f'(x)?3x2?3=0,得x??1,
当x??1时,f/(x)>0,当?1?x?1时,f/(x)<0,当x?1时,f/(x)>0, 故f(x)的极小值、极大值分别为f(?1)?3、f(1)??1, 而f(?3)??17、f(0)?1
故函数f(x)?x3?3x?1在[-3,0]上的最大值、最小值分别是3、-17。
●经典例题选讲
例1. 已知函数y?xf?(x)的图象如图所示(其中 f?(x)是函数f(x)的导函数),下面四个图象中y?f(x)的图象大致是
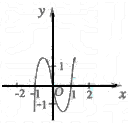
( )
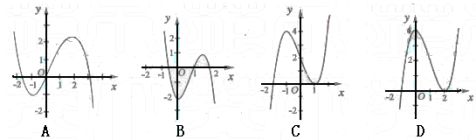
[解析]:由函数y?xf?(x)的图象可知: 当x??1时, xf?(x)<0,f?(x)>0,此时f(x)增 当?1?x?0时,xf?(x)>0,f?(x)<0,此时f(x)减
当0?x?1时,xf?(x)<0,f?(x)<0,此时f(x)减 当x?1时,xf?(x)>0,f?(x)>0,此时f(x)增 故选C
例2.设f(x)?ax3?x恰有三个单调区间,试确定a的取值范围,并求其单调区间。
解:f?(x)?3ax2?1
若a?0,f?(x)?0对x?(??,??)恒成立,此时f(x)只有一个单调区间,矛盾
若a?0,f?(x)?1?0 ∴ x?(??,??),f(x)也只有一个单调区间,矛盾
若a?0 ∵ f?(x)?3a(x?单调区间
∴ a?0且单调减区间为(??,?(?1
|a|,1
|a|) 1|a|)和(1|a|,??),单调增区间为1|a|)?(x?1|a|),此时f(x)恰有三个
例3. 已知函数f(x)?x3?bx2?ax?d的图象过点P(0,2),且在点M(?1,f(?1))处的切线方程为6x?y?7?0. (Ⅰ)求函数y?f(x)的解析式; (Ⅱ)求函数y?f(x)的单调区间. 解:(Ⅰ)由f(x)的图象经过P(0,2),知d=2, 所以f(x)?x3?bx2?cx?2, f?(x)?3x2?2bx?c.
由在M(?1,f(?1))处的切线方程是6x?y?7?0,知
?6?f(?1)?7?0,即f(?1)?1,f?(?1)?6.
?3?2b?c?6,?2b?c?3,??即?解得b?c??3. ?1?b?c?2?1.b?c?0,??
故所求的解析式是 f(x)?x3?3x2?3x?2.
(Ⅱ)f?(x)?3x2?6x?3.令3x2?6x?3?0,即x2?2x?1?0. 解得 x1?1?2,x2?1?2. 当x?1?2,或x?1?2时,f?(x)?0; 当1?2?x?1?2时,f?(x)?0. 故f(x)?x3?3x2?3x?2在(??,1?2)内是增函数, 在(1?2,1?2)内是减函数,在(1?2,??)内是增函数. 例4. 设函数f?x??x3?bx2?cx(x?R),已知g(x)?f(x)?f?(x)是奇函数。
(Ⅰ)求b、c的值。 (Ⅱ)求g(x)的单调区间与极值。 解:(Ⅰ)∵f?x??x3?bx2?cx,∴f??x??3x2?2bx?c。从而
g(x)?f(x)?f?(x)?x3?bx2?cx?(3x2?2bx?c)=x3?(b?3)x2?(c?2b)x?c是
一个奇函数,所以g(0)?0得c?0,由奇函数定义得b?3; (Ⅱ)由(Ⅰ)知g(x)?x3?6x,从而g?(x)?3x2?6,由此可知,
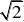
(??,
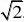
和??)是函数g(x
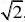
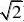
)是单调递增区间;(是函数
g(x)是单调递减区间;
g(x
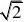
)在x?
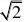
g(x
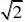
)在x?
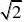
?。
例5. 已知f(x)=x3?ax2?bx?c在x=1,x=?时,都取得极值。
(1)求a、b的值。
(2)若对x?[?1,2],都有f(x)?恒成立,求c的取值范围。 解:(1)由题意f/(x)=3x2?2ax?b的两个根分别为1和? 由韦达定理,得:1?=? 则a??,b??2 1
2232ab2,?1?(?) 333231c23
(2)由(1),有f(x)=x3?x2?2x?c,f/(x)=3x2?x?2 当x?[?1,?)时,f/(x)?0,当x?(?,1)时,f/(x)?0,当x?(1,2]时,
f/(x)?0,
2
3
12
23
当x??时,f(x)有极大值
23221
?c,f(?1)??c,f(2)?2?c, 272
∴ 当x?[?1,2],f(x)的最大值为f(2)?2?c 对x?[?1,2],都有f(x)?恒成立,∴2?c?, 解得0?c?2?1,或c??2?1,
例6. 已知x?1是函数f(x)?mx3?3(m?1)x2?nx?1的一个极值点,其中
m,n?R,m?0,
1c1c
(I)求m与n的关系式; (II)求f(x)的单调区间;
(III)当x???1,1?时,函数y?f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
解:(I)f?(x)?3mx2?6(m?1)x?n因为x?1是函数f(x)的一个极值点,
所以f?(1)?0,即3m?6(m?1)?n?0,所以n?3m?6
?2??
(II)由(I)知,f?(x)?3mx2?6(m?1)x?3m?6=3m(x?1)?x??1????
?
?
m??
当m?0时,有1?1?
如下表:
x
f?(x) f(x)
2
,当x变化时,f(x)与f?(x)的变化m
2??
??,1??? m??
?0
1?
2
m
2??1?,1? ?
m???0
1 0 极大值
?1,???
?0
0 极小值
调调递减 单调递增 单调递减
2?故有上表知,当m?0时,f(x)在???,1???单调递减, ?m?
在(1?2,1)单调递增,在(1,??)上单调递减. m
(III)由已知得f?(x)?3m,即mx2?2(m?1)x?2?0
又m?0所以x2?(m?1)x?
① 设g(x)?x2?2(1?)x?
立, 22??g(?1)?0?1?2???0所以?解之得 ??mm?g(1)?0???1?0
4??m又m?0 3
4所以??m?0 31m2,其函数开口向上,由题意知①式恒成m2m222?0即x2?(m?1)x??0,x???1,1?mmm
?即m的取值范围为??,0?? 3??4
例7:(2009天津理20)已知函数f(x)?(x2?ax?2a2?3a)ex(x?R),其中a?R
(1) 当a?0时,求曲线y?f(x)在点(1,f(1))处的切线的斜率;
(2) 当a?时,求函数f(x)的单调区间与极值。
本小题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算能力及分类讨论的思想方法。满分12分。
解:(I)当a?0时,f(x)?x2ex,f'(x)?(x2?2x)ex,故f'(1)?3e.
所以曲线y?f(x)在点(1,f(1))处的切线的斜率为3e. 23
(II)f'(x)??x2?(a?2)x?2a2?4a?ex.
令f'(x)?0,解得x??2a,或x?a?2.由a?
2
知,?2a?a?2. 3
以下分两种情况讨论。
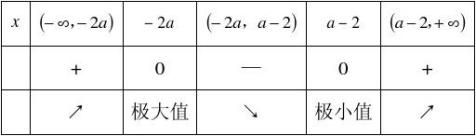
(1)若a>,则?2a<a?2.当x变化时,f'(x),f(x)的变化情况如下表:
23
所以f(x)在(??,?2a),(a?2,??)内是增函数,在(?2a,a?2)内是减函数.
函数f(x)在x??2a处取得极大值f(?2a),且f(?2a)?3ae?2a. 函数f(x)在x?a?2处取得极小值f(a?2),且f(a?2)?(4?3a)ea?2.
(2)若a<,则?2a>a?2,当x变化时,f'(x),f(x)的变化情况如下表:

2
3
所以f(x)在(??,a?2),(?2a,??)内是增函数,在(a?2,?2a)内是减函数。
函数f(x)在x?a?2处取得极大值f(a?2),且f(a?2)?(4?3a)ea?2.
