高中函数对称性总结
安徽省太湖县朴初中学/苏深强
新课标高中数学教材上就函数的性质着重讲解了单调性、奇偶性、周期性,但在考试测验甚至高考中不乏对函数对称性、连续性、凹凸性的考查。尤其是对称性,因为教材上对它有零散的介绍,例如二次函数的对称轴,反比例函数的对称性,三角函数的对称性,因而考查的频率一直比较高。以笔者的经验看,这方面一直是教学的难点,尤其是抽象函数的对称性判断。所以这里我对高中阶段所涉及的函数对称性知识做一个粗略的总结。
一、对称性的概念及常见函数的对称性
1、对称性的概念
①函数轴对称:如果一个函数的图像沿一条直线对折,直线两侧的图像能够完全重合,则称该函数具备对称性中的轴对称,该直线称为该函数的对称轴。
②中心对称:如果一个函数的图像沿一个点旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,该点称为该函数的对称中心。
2、常见函数的对称性(所有函数自变量可取有意义的所有值)
①常数函数:既是轴对称又是中心对称,其中直线上的所有点均为它的对称中心,与该直线相垂直的直线均为它的对称轴。
②一次函数:既是轴对称又是中心对称,其中直线上的所有点均为它的对称中心,与该直线相垂直的直线均为它的对称轴。
③二次函数:是轴对称,不是中心对称,其对称轴方程为x=-b/(2a)。
④反比例函数:既是轴对称又是中心对称,其中原点为它的对称中心,y=x与y=-x均为它的对称轴。 ⑤指数函数:既不是轴对称,也不是中心对称。
⑥对数函数:既不是轴对称,也不是中心对称。
⑦幂函数:显然幂函数中的奇函数是中心对称,对称中心是原点;幂函数中的偶函数是轴对称,对称轴是y轴;而其他的幂函数不具备对称性。
⑧正弦函数:既是轴对称又是中心对称,其中(kπ,0)是它的对称中心,x=kπ+π/2是它的对称轴。
⑨正弦型函数:正弦型函数y=Asin(ωx+φ)既是轴对称又是中心对称,只需从ωx+φ=kπ中解出x,就是它的对称中心的横坐标,纵坐标当然为零;只需从ωx+φ=kπ+π/2中解出x,就是它的对称轴;需要注意的是如果图像向上
向下平移,对称轴不会改变,但对称中心的纵坐标会跟着变化。
⑩余弦函数:既是轴对称又是中心对称,其中x=kπ是它的对称轴,(kπ+π/2,0)是它的对称中心。
⑾正切函数:不是轴对称,但是是中心对称,其中(kπ/2,0)是它的对称中心,容易犯错误的是可能有的同学会误以为对称中心只是(kπ,0)。
⑿对号函数:对号函数y=x+a/x(其中a>0)因为是奇函数所以是中心对称,原点是它的对称中心。但容易犯错误的是同学们可能误以为最值处是它的对称轴,例如在处理函数y=x+1/x时误以为会有f0.5)=f(1.5),我在教学时总是问学生:你可看见过老师将“√”两边画得一样齐?学生们立刻明白并记忆深刻。
⒀三次函数:显然三次函数中的奇函数是中心对称,对称中心是原点,而其他的三次函数是否具备对称性得因题而异。
⒁绝对值函数:这里主要说的是y=f(│x│)和y=│f(x)│两类。前者显然是偶函数,它会关于y轴对称;后者是把x轴下方的图像对称到x轴的上方,是否仍然具备对称性,这也没有一定的结论,例如y=│lnx│就没有对称性,而y=│sinx│却仍然是轴对称。
二、函数的对称性猜测
1、具体函数特殊的对称性猜测
①一个函数一般是不会关于x轴的
这是由函数定义决定的,因为一个x不会对应两个y的值。但我们在此略微引申,一个曲线是可能关于x轴对称的。
例1判断曲线y^2=4x的对称性。
②函数关于y轴对称
例2判断函数y=cos(sin(x))的对称性。
③函数关于原点对称
例3判断函数y=(x^3)×sinx的对称性。
④函数关于y=x对称
例4判断函数y=1/x的对称性。
⑤函数关于y=-x对称
例5判断函数y=-4/x的对称性。
我总结为:设(x,y)为原曲线图像上任一点,
如果(x,-y)也在图像上,则该曲线关于x轴对称;
如果(-x,y)也在图像上,则该曲线关于y轴对称;
如果(-x,-y)也在图像上,则该曲线关于原点对称;
如果(y,x)也在图像上,则该曲线关于y=x对称;
如果(-y,-x)也在图像上,则该曲线关于y=-x轴对称。
2、抽象函数的对称性猜测
①轴对称
例6如果函数y=f(x)满足f(x+1)=f(4-x),求该函数的所有对称轴。(任意取值代入例如x=0有f(1)=f(4),正中间2.5,从而该函数关于x=2.5对称)
例7如果函数y=f(x)满足f(x)=f(-x),求该函数的所有对称轴。(按上例一样的方法可以猜出对称轴为x=0,可见偶函数是特殊的轴对称)
例8如果f(x)为偶函数,并且f(x+1)=f(x+3),求该函数的所有对称轴。(因为f(x+1)=f(-x-3),按上例可以猜出对称轴x=-1,又因为它以2为周期,所以x=k是它所有的对称轴,k∈Z)
②中心对称
例9如果函数y=f(x)满足f(3+x)+f(4-x)=6,求该函数的对称中心。(因为自变量加起来为7时函数值的和始终为6,所以中点固定为(3.5,3),这就是它的对称中心)
例10如果函数y=f(x)满足f(-x)+f(x)=0,求该函数的所有对称中心。(按上例一样的方法可以猜出对称中心为(0,0),可见奇函数是特殊的中心对称)
例11如果f(x)为奇函数,并且f(x+1)+f(x+3)=0,求该函数的所有对称中心和对称轴。(由周期性定义知周期为4,又f(x+1)=-f(x+3),从而f(x+1)=f(-x-3),按上例知x=-1为对称轴,所以x=-1+2n为对称轴,(2k,0)为对称中心,其中k∈Z)
我总结为:
①当括号里面x前面的符号一正一负时告诉我们的就是对称性,其中的对称为多少我们可以用特殊值代入来猜测,这里并不主张记结论,因为很容易与后面的结论相混淆。
②而当x前面的符号相同时告诉我们的是周期性。例如f(x+1)=f(x-5)是告诉我们它以6为周期。
③当x前面的符号相同,同时告诉我们奇偶性时我们也可以推出对称性,因为奇偶性有制造负号的能力。
3、两个抽象函数之间的对称性猜测
例12求y=f(x+2)与y=f(1-x)的对称轴方程。(当第一个函数的x取0时,值为f(2),这时第二个函数的x必须取-1才也对应那么多,他们的正中间为-1.5,因而猜测对称轴为x=-1.5)
我总结为:
①当括号里面x前面的符号一正一负时告诉我们的就是对称性,其中的对称为多少我们仍然可以用特殊值代入来猜测,这里仍然不主张记结论,因为很容易与前面的结论相混淆。
②而当x前面的符号相同时告诉我们的是图像平移。例如y=f(x+2)与y=f(x-1),前者是由后者向左移三个单位得到。
三、对称性的证明
如果在解答大题时仅仅猜测出结论是不够的,我们要辅以完整的证明才行。
1、一个函数的对称性证明
例13证明如果函数y=f(x)满足f(a+x)=f(b-x),则该函数关于直线x=(a+b)/2对称。
证明:在y=f(x)上任取点(m,n),则n=f(m),而点(m,n)关于x=(a+b)/2的对称点为(a+b-m,n),又因为f(a+b-m)=f(a+(b-m))=f(b-(b-m))=f(m)=n,这正表明(a+b-m,n)也在原函数图像上,从而原函数关于直线x=(a+b)/2对称。
我总结为:核心是间接法,即在函数上任取一点,对称点如果仍在函数图像上,我们就可以下结论该函数关于它对称。
2、两个函数之间的对称性的证明
例14证明函数y=f(a+x)与函数y=f(b-x)关于直线x=(b-a)/2对称。(注意不是(a-b)/2,证明的方法类似于上例方法)
我总结为:仍是间接法,但是多一次,需在函数上任取一点,对称点如果在对方函数图像上,同时在对方函数上任取一点,对称点又在该函数图像上,我们才可以下结论该函数关于它对称。取两次的原因是以免两个图像一个只是另一个对称过来图像的一部分。
3、特别地关于y=x对称性的证明
例15证明y=(2x+1)/(3x-2)关于y=x对称。(只需求出它的反函数是自己即可)
我总结为:
①一个函数自身关于y=x对称不需要用上面的间接法,只需要证明它的反函数是自己就可以了。
②两个函数关于y=x对称性证明也不需要用上面那么繁琐的方法,只需证明两个函数互为反函数,即求一个的反函数为另外一个就可以了。
③反过来这句话也成立,如果需要证明两个函数互为反函数,只需要证明它们的图像关于y=x对称即可。
四、对称性的运用
1、求值
例16已知f(x)=4^x/(4^x+1),求f(-4)+f(-3)+f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)+f(4)的值。(我们只需要考虑当两个自变量加起来为0时函数值的和是否为定值,验证果然。而这里显然隐含的是函数的对称性)
我总结为:“配对”,对称性主要是考查一对函数值之间的关系。
2、“对称性+对称性”可以推导出周期性
例17如果函数y=f(x)满足f(x+3)=f(2-x)和f(4+x)=f(5-x),求该函数的最小正周期。(因为f(x+3)=f(2-x)=f(4+(-2-x)) =f(5-(-2-x))=f(7+x)所以周期为4)
我总结为:两个对称性拼起来就可以将里面的符号化为同号,从而得出周期性。
3、“奇偶性+对称性”可以推导出周期性
这在前面已经提到,还是因为奇偶性有制造负号的能力。
4、三角函数的奇偶性
例18如果函数y=3sin(2x+θ+π/4)(其中0<θ<π)是奇函数,求θ的值。(2x+θ+π/4=kπ,而x=0,所以θ+π/4=kπ,在要求的范围上只有θ=3π/4)
我总结为:几乎所有的三角函数的奇偶性都是当对称性来使用,先求出所有的对称轴,然后y轴是其中的一条(或者先求出所有的对称中心,然后原点是其中的一个)。
5、关于y=x对称的应用
例19求函数f(x)=e^(x+1)与函数g(x)=ln(x+1)的对称轴方程。(因为f(x)=e^x与g(x)=lnx互为反函数,关于y=x对称,而f(x)=e^(x+1)是由f(x)=e^x向左移一个单位得到,g(x)=ln(x+1)也是由g(x)=lnx向左移一个单位得到,因而对称轴也跟着左移一个单位,即y=x+1)
6、对称性的本义
例20如果y=asinx+bcosx关于x=π/4对称,求直线ax+by+3=0的直线的斜率。(既然关于x=π/4对称,则f(0)=f(π/2)
代入求出a和b的关系即可)
我总结为:对称性的本义就是关于对称中心(或对称轴)对称的两个自变量的函数值的紧密关系。
这就是我关于函数对称性的简单总结,难免挂一漏万,还请大家批评指正。最后笔者建议新课标教材能类似于函数周期性,给对称性独立的一节,介绍它的概念和运用,同步练习上也给安排一节对它的独立的练习,这样教师在教学上就可以用适当引申的方法,而不是象现在这样,老师忙于查资料,学生忙于记笔记,耗时费力地试图尽可能系统而完整地补充。
结论1:若对于函数y=f(x),
中心对称。
即若函数图象关于点(a,b)对称,则满足:f(a-x)+f(a+x)=2b或f(x)+f(2a-x)=2b
,有f(a+x)+f(a-x)=2b,则函数y=f(x)的图象关于点(a,b)
下面是结论2应用的例子,
例5 函数y=f(x)的图象与函数y=g(x)的图象关于点(-1,-2)对称,已知f(3)
=4,求g(-5)的值。
解:由结论2可知,g(x)=一4-f(-2-x),
∴g(-5)=-4-f〔-2-(-5)〕
即 g(-5)=-4-f(3)=-4-4, ∴g(-5)=-8
第二篇:函数对称性、周期性和奇偶性规律总结
函数对称性、周期性和奇偶性
关岭民中数学组
(一)、同一函数的函数的奇偶性与对称性:(奇偶性是一种特殊的对称性)
1、奇偶性:(1) 奇函数关于(0,0)对称,奇函数有关系式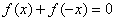
(2)偶函数关于y(即x=0)轴对称,偶函数有关系式 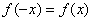
2、奇偶性的拓展 : 同一函数的对称性
(1)函数的轴对称:
函数 关于
关于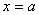 对称
对称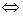
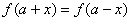
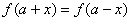 也可以写成
也可以写成 或
或 
若写成: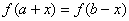 ,则函数
,则函数 关于直线
关于直线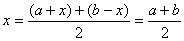 对称
对称
证明:设点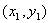 在
在 上,通过
上,通过 可知,
可知,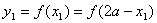 ,即点
,即点 上,而点
上,而点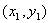 与点
与点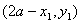 关于x=a对称。得证。
关于x=a对称。得证。
说明:关于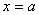 对称要求横坐标之和为
对称要求横坐标之和为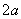 ,纵坐标相等。
,纵坐标相等。
∵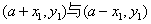 关于
关于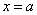 对称,∴函数
对称,∴函数 关于
关于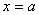 对称
对称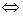
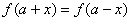
∵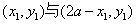 关于
关于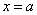 对称,∴函数
对称,∴函数 关于
关于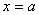 对称
对称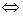

∵ 关于
关于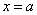 对称,∴函数
对称,∴函数 关于
关于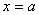 对称
对称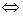

(2)函数的点对称:
函数 关于点
关于点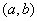 对称
对称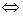
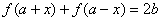
 或
或 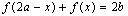
若写成: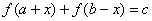 ,函数
,函数 关于点
关于点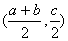 对称
对称
证明:设点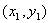 在
在 上,即
上,即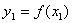 ,通过
,通过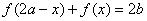
可知,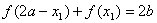 ,所以
,所以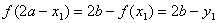 ,所以点
,所以点
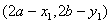 也在
也在 上,而点
上,而点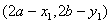 与
与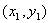 关于
关于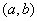 对称
对称
得证。
说明: 关于点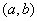 对称要求横坐标之和为
对称要求横坐标之和为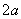 ,纵坐标之和为
,纵坐标之和为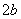 ,如
,如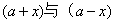 之和为
之和为 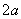 。
。
(3)函数 关于点
关于点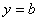 对称:假设函数关于
对称:假设函数关于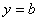 对称,即关于任一个
对称,即关于任一个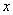 值,都有两个y值与其对应,显然这不符合函数的定义,故函数自身不可能关于
值,都有两个y值与其对应,显然这不符合函数的定义,故函数自身不可能关于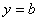 对称。但在曲线c(x,y)=0,则有可能会出现关于
对称。但在曲线c(x,y)=0,则有可能会出现关于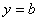 对称,比如圆
对称,比如圆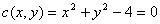 它会关于y=0对称。
它会关于y=0对称。
(4)复合函数的奇偶性的性质定理:
性质1、复数函数y=f[g(x)]为偶函数,则f[g(-x)]=f[g(x)]。
复合函数y=f[g(x)]为奇函数,则f[g(-x)]=-f[g(x)]。
性质2、复合函数y=f(x+a)为偶函数,则f(x+a)=f(-x+a);
复合函数y=f(x+a)为奇函数,则f(-x+a)=-f(a+x)。
性质3、复合函数y=f(x+a)为偶函数,则y=f(x)关于直线x=a轴对称。
复合函数y=f(x+a)为奇函数,则y=f(x)关于点(a,0)中心对称。
总结:x的系数一个为1,一个为-1,相加除以2,可得对称轴方程
总结:x的系数一个为1,一个为-1,f(x)整理成两边,其中一个的系数是为1,另一个为-1,存在对称中心。
总结:x的系数同为为1,具有周期性。
(二)、两个函数的图象对称性
1、 与
与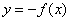 关于X轴对称。
关于X轴对称。
证明:设 上任一点为
上任一点为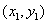 则
则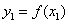 ,所以
,所以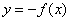 经过点
经过点
∵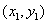 与
与 关于X轴对称,∴
关于X轴对称,∴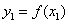 与
与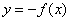 关于X轴对称.
关于X轴对称.
注:换种说法: 与
与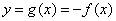 若满足
若满足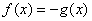 ,即它们关于
,即它们关于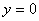 对称。
对称。
2、 与
与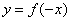 关于Y轴对称。
关于Y轴对称。
证明:设 上任一点为
上任一点为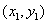 则
则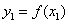 ,所以
,所以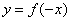 经过点
经过点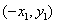
∵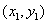 与
与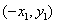 关于Y轴对称,∴
关于Y轴对称,∴ 与
与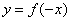 关于Y轴对称。
关于Y轴对称。
注:因为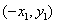 代入
代入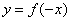 得
得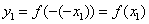 所以
所以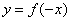 经过点
经过点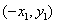
换种说法: 与
与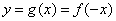 若满足
若满足 ,即它们关于
,即它们关于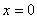 对称。
对称。
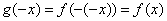
3、 与
与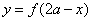 关于直线
关于直线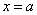 对称。
对称。
证明:设 上任一点为
上任一点为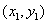 则
则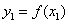 ,所以
,所以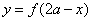 经过点
经过点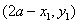
∵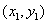 与
与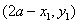 关于
关于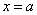 轴对称,∴
轴对称,∴ 与
与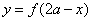 关
关
于直线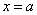 对称。
对称。
注:换种说法: 与
与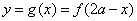 若满足
若满足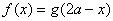 ,即它们关于
,即它们关于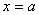 对称。
对称。
4、 与
与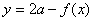 关于直线
关于直线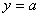 对称。
对称。
证明:设 上任一点为
上任一点为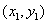 则
则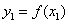 ,所以
,所以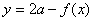 经过点
经过点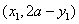
∵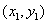 与
与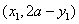 关于
关于 轴对称,∴
轴对称,∴ 与
与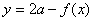 关于直线
关于直线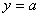 对称.
对称.
注:换种说法: 与
与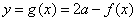 若满足
若满足 ,即它们关于
,即它们关于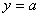 对称。
对称。
5、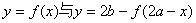 关于点(a,b)对称。
关于点(a,b)对称。
证明:设 上任一点为
上任一点为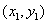 则
则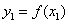 ,所以
,所以 经过点
经过点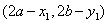
∵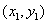 与
与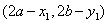 关于点(a,b)对称,∴
关于点(a,b)对称,∴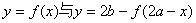 关于点(a,b)对称.
关于点(a,b)对称.
注:换种说法: 与
与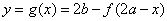 若满足
若满足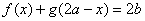 ,即它们关于点(a,b)对称。
,即它们关于点(a,b)对称。
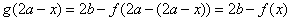
6、 与
与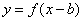 关于直线
关于直线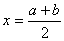 对称。
对称。
证明:设 上任一点为
上任一点为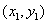 则
则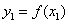 ,所以
,所以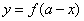 经过点
经过点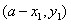 ,
, 经过点
经过点 ,∵
,∵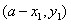 与
与 关于直线
关于直线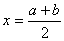 对称,
对称,
∴ 与
与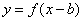 关于直线
关于直线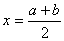 对称。
对称。
三、总规律:定义在R上的函数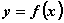 ,在对称性、周期性和奇偶性这三条性质中,只要有两条存在,则第三条一定存在。
,在对称性、周期性和奇偶性这三条性质中,只要有两条存在,则第三条一定存在。
一、 同一函数的周期性、对称性问题(即函数自身)
(一)、函数的周期性:对于函数 ,如果存在一个不为零的常数T,使得当x取定义域内的每一个值时,都有
,如果存在一个不为零的常数T,使得当x取定义域内的每一个值时,都有 都成立,那么就把函数
都成立,那么就把函数 叫做周期函数,不为零的常数T叫做这个函数的周期。如果所有的周期中存在着一个最小的正数,就把这个最小的正数叫做最小正周期。
叫做周期函数,不为零的常数T叫做这个函数的周期。如果所有的周期中存在着一个最小的正数,就把这个最小的正数叫做最小正周期。
1、周期性:
(1)函数 满足如下关系式,则
满足如下关系式,则
A、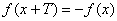 B、
B、
C、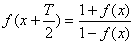 或
或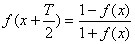 (等式右边加负号亦成立)
(等式右边加负号亦成立)
D、其他情形
(2)函数 满足
满足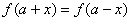 且
且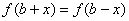 ,则可推出
,则可推出
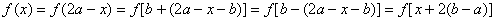 即可以
即可以
得到 的周期为2(b-a),即可以得到“如果函数在定义域内关于垂直于x
的周期为2(b-a),即可以得到“如果函数在定义域内关于垂直于x
轴两条直线对称,则函数一定是周期函数”
(3)如果奇函数满足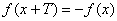 则可以推出其周期是2T,且可以推出对称
则可以推出其周期是2T,且可以推出对称
轴为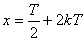
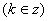 ,根据
,根据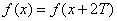 可以找出其对称中心为
可以找出其对称中心为
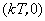
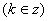 (以上
(以上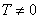 )
)
如果偶函数满足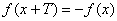 则亦可以推出周期是2T,且可以推出对称中心为
则亦可以推出周期是2T,且可以推出对称中心为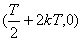
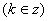 ,根据
,根据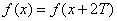 可以推出对称轴为
可以推出对称轴为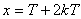
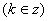 (以上
(以上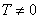 )
)
(4)如果奇函数 满足
满足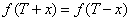 (
( ),则函数
),则函数 是
是
以4T为周期的周期性函数。如果偶函数 满足
满足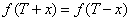
( ),则函数
),则函数 是以2T为周期的周期性函数。
是以2T为周期的周期性函数。
定理1:若函数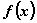 在R上满足
在R上满足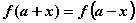 ,且
,且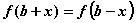 (其
(其
中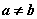 ),则函数
),则函数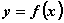 以
以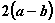 为周期.
为周期.
定理2:若函数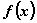 在R上满足
在R上满足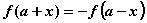 ,且
,且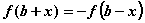
(其中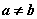 ),则函数
),则函数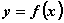 以
以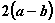 为周期.
为周期.
定理3:若函数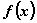 在R上满足
在R上满足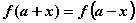 ,且
,且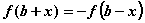 (其
(其
中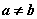 ),则函数
),则函数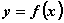 以
以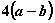 为周期.
为周期.
定理4:若函数f(x)的图像关于直线x=a和x=b都对称,则f(x)是周期函数,2(b-a)是它的一个周期(未必是最小正周期)。
定理5:若函数f(x)的图像关于点(a,c)和(b,c)都成中心对称,则f(x)是周期函数,2(b-a)是它的一个周期(未必是最小正周期)。
定理6:若函数f(x)关于点(a,c)和x=b都对称,则f(x)是周期,4(b-a)是它的一个周期(未必是最小正周期)。
定理7:若函数f(x)满足f(x-a)=f(x+a)(a>0),则f(x)是周期函数,2a是它的一个周期。
定理8:若函数f(x)满足f(x+a)=-f(x)(a>0)(或f(x+a)=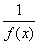 或f(x+a)=-
或f(x+a)=-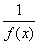 )则f(x)周期函数,2a是它的一个周期。
)则f(x)周期函数,2a是它的一个周期。
定理9:若函数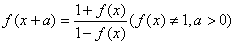 ,则f(x)是周期函数,4a是它的一个周期。
,则f(x)是周期函数,4a是它的一个周期。
若f(x)满足 ,则f(x)是周期函数,2a是它的一个周期。
,则f(x)是周期函数,2a是它的一个周期。
