复 数
1.复数的概念:
(1)虚数单位i;
(2)复数的代数形式z=a+bi,(a, b∈R);
(3)复数的实部、虚部、虚数与纯虚数。
2.复数集
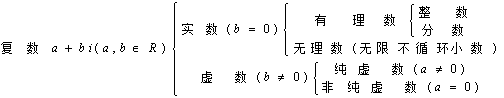
3.复数a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位,当b=0时,a+bi就是实数,当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。
应特别注意,a=0仅是复数a+bi为纯虚数的必要条件,若a=b=0,则a+bi=0是实数。
4.复数的四则运算
若两个复数z1=a1+b1i,z2=a2+b2i,
(1)加法:z1+z2=(a1+a2)+(b1+b2)i;
(2)减法:z1-z2=(a1-a2)+(b1-b2)i;
(3)乘法:z1·z2=(a1a2-b1b2)+(a1b2+a2b1)i;
(4)除法: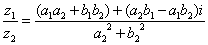 ;
;
(5)四则运算的交换率、结合率;分配率都适合于复数的情况。
(6)特殊复数的运算:
①  (n为整数)的周期性运算; ②(1±i)2 =±2i;
(n为整数)的周期性运算; ②(1±i)2 =±2i;
③ 若ω=-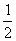 +
+ i,则ω3=1,1+ω+ω2=0.
i,则ω3=1,1+ω+ω2=0.
5.共轭复数与复数的模
(1)若z=a+bi,则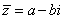 ,
,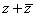 为实数,
为实数, 为纯虚数(b≠0).
为纯虚数(b≠0).
(2)复数z=a+bi的模|Z|=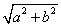 , 且
, 且 =a2+b2.
=a2+b2.
6.根据两个复数相等的定义,设a, b, c, d∈R,两个复数a+bi和c+di相等规定为a+bi=c+di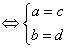 . 由这个定义得到a+bi=0
. 由这个定义得到a+bi=0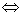
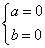 .
.
两个复数不能比较大小,只能由定义判断它们相等或不相等。
4.复数a+bi的共轭复数是a-bi,若两复数是共轭复数,则它们所表示的点关于实轴对称。若b=0,则实数a与实数a共轭,表示点落在实轴上。
6.复数的除法是复数乘法的逆运算将满足(c+di)(x+yi)=a+bi (c+bi≠0)的复数x+yi叫做复数a+bi除以复数c+di的商。
由于两个共轭复数的积是实数,因此复数的除法可以通过将分母实化得到,即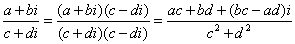 .
.
7.复数a+bi的模的几何意义是指表示复数a+bi的点到原点的距离。
(二)典型例题讲解
1.复数的概念
例1.实数m取什么数值时,复数z=m+1+(m-1)i是(1)实数?(2)虚数?(3)纯虚数?(4)对应的点Z在第三象限?
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y.
例4.当m为何实数时,复数z= +(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
+(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
例5.计算:i+i2+i3+……+i2005.
例8.使不等式m2-(m2-3m)i<(m2-4m+3)i+10成立的实数m= .
例9.已知z=x+yi(x,y∈R),且 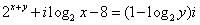 ,求z.
,求z.
例10.已知x为纯虚数,y是实数,且2x-1+i=y-(3-y)i,求x、y的值.
2.复数的四则运算
例1.计算:
(1)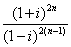 ,n∈N+;
,n∈N+;
(2)若ω=-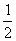 +
+ i,ω3=1,计算
i,ω3=1,计算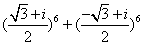 ;
;
(3)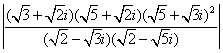 ;
;
(4)S=1+2i+3i2+4i3+……+100i99.
例2.已知复数z满足|z-2|=2,z+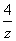 ∈R,求z.
∈R,求z.
例4.复数z满足(z+1)(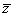 +1)=|
+1)=|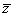 |2,且
|2,且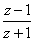 为纯虚数,求z.
为纯虚数,求z.
例5.复数z满足(1+2i)z+(3-10i)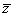 =4-34i,求z.
=4-34i,求z.
例6.设z是虚数,ω=z+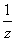 是实数,且-1<ω<2,
是实数,且-1<ω<2,
(1)求|z|的值及z的实部的取值范围;(2)设u=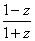 ,求证u为 纯虚数;
,求证u为 纯虚数;
(3)求ω-u2的最小值。
7.已知关于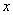 的方程
的方程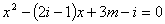 有实根,求实数
有实根,求实数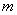 的取值。
的取值。
1..若复数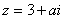 满足条件
满足条件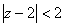 ,则实数
,则实数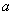 的取值范围是( )
的取值范围是( )
A.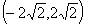 B.
B.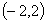 C.
C.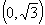 D.
D.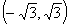
3.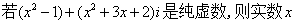 的值为 ( )
的值为 ( )
 .
.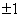
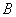 .1
.1 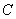 .
.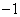
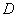 .
. 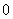
8.如果复数z=(a2-3a+2)+(a-1)i为纯虚数,则实数a的值 ( ).
A.等于1或2 B.等于1 C.等于2 D.不存在
13.已知 ,其中
,其中 ,则
,则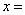 ,
,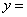 .
.
14.复数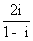 在复平面内所对应的点的坐标为 .
在复平面内所对应的点的坐标为 .
15.设复数z满足i(z+1)=-3+2i(i为虚数单位),则z等于___ _____.
16.若复数z满足z=i(2-z)(i是虚数单位),则z=________.
17.(本题满分12分)已知 ,复数
,复数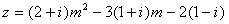 ,
,
(1)写出复数z的代数形式;
(2)当m为何值时,z=0?当m为何值时,z是纯虚数?
第二篇:高考复数知识点精华总结
复 数
1.复数的概念:
(1)虚数单位i;
(2)复数的代数形式z=a+bi,(a, b∈R);
(3)复数的实部、虚部、虚数与纯虚数。
2.复数集

3.复数a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位,当b=0时,a+bi就是实数,当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。
应特别注意,a=0仅是复数a+bi为纯虚数的必要条件,若a=b=0,则a+bi=0是实数。
4.复数的四则运算
若两个复数z1=a1+b1i,z2=a2+b2i,
(1)加法:z1+z2=(a1+a2)+(b1+b2)i;
(2)减法:z1-z2=(a1-a2)+(b1-b2)i;
(3)乘法:z1·z2=(a1a2-b1b2)+(a1b2+a2b1)i;
(4)除法: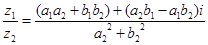 ;
;
(5)四则运算的交换率、结合率;分配率都适合于复数的情况。
(6)特殊复数的运算:
① 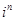 (n为整数)的周期性运算; ②(1±i)2 =±2i;
(n为整数)的周期性运算; ②(1±i)2 =±2i;
③ 若ω=-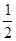 +
+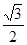 i,则ω3=1,1+ω+ω2=0.
i,则ω3=1,1+ω+ω2=0.
5.共轭复数与复数的模
(1)若z=a+bi,则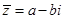 ,
,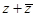 为实数,
为实数, 为纯虚数(b≠0).
为纯虚数(b≠0).
(2)复数z=a+bi的模|Z|= , 且
, 且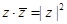 =a2+b2.
=a2+b2.
6.根据两个复数相等的定义,设a, b, c, d∈R,两个复数a+bi和c+di相等规定为a+bi=c+di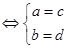 . 由这个定义得到a+bi=0
. 由这个定义得到a+bi=0
 .
.
两个复数不能比较大小,只能由定义判断它们相等或不相等。
4.复数a+bi的共轭复数是a-bi,若两复数是共轭复数,则它们所表示的点关于实轴对称。若b=0,则实数a与实数a共轭,表示点落在实轴上。
5.复数的加法、减法、乘法运算与实数的运算基本上没有区别,最主要的是在运算中将i2=-1结合到实际运算过程中去。
如(a+bi)(a-bi)= a2+b2
6.复数的除法是复数乘法的逆运算将满足(c+di)(x+yi)=a+bi (c+bi≠0)的复数x+yi叫做复数a+bi除以复数c+di的商。
由于两个共轭复数的积是实数,因此复数的除法可以通过将分母实化得到,即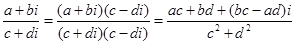 .
.
7.复数a+bi的模的几何意义是指表示复数a+bi的点到原点的距离。
(二)典型例题讲解
1.复数的概念
例1.实数m取什么数值时,复数z=m+1+(m-1)i是(1)实数?(2)虚数?(3)纯虚数?(4)对应的点Z在第三象限?
解:复数z=m+1+(m-1)i中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,
∴ (1)m=1时,z是实数; (2)m≠1时,z是虚数;
(3)当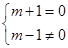 时,即m=-1时,z是纯虚数;
时,即m=-1时,z是纯虚数;
(4)当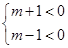 时,即m<-1时,z对应的点Z在第三象限。
时,即m<-1时,z对应的点Z在第三象限。
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y.
解:根据复数相等的意义,得方程组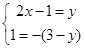 ,得x=
,得x=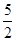 , y=4.
, y=4.
例4.当m为何实数时,复数z=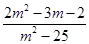 +(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
+(m2+3m-10)i;(1)是实数;(2)是虚数;(3)是纯虚数.
解:此题主要考查复数的有关概念及方程(组)的解法.
(1)z为实数,则虚部m2+3m-10=0,即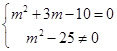 ,
,
解得m=2,∴ m=2时,z为实数。
(2)z为虚数,则虚部m2+3m-10≠0,即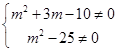 ,
,
解得m≠2且m≠±5. 当m≠2且m≠±5时,z为虚数.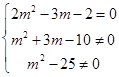 ,
,
解得m=-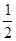 , ∴当m=-
, ∴当m=-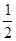 时,z为纯虚数.
时,z为纯虚数.
诠释:本题应抓住复数分别为实数、虚数、纯虚数时相应必须具备的条件,还应特别注意分母不为零这一要求.
例5.计算:i+i2+i3+……+i2005.
解:此题主要考查in的周期性.
i+i2+i3+……+i2005=(i+i2+i3+i4)+……+(i2001+i2002+ i2003+i2004)+i2005
=(i-1-i+1)+ (i-1-i+1)+……+(i-1-i+1)+i
=0+0+……+0+i=i.
或者可利用等比数列的求和公式来求解(略) 诠释:本题应抓住in的周期及合理分组.
例8.使不等式m2-(m2-3m)i<(m2-4m+3)i+10成立的实数m= .
解:此题主要考查复数能比较大小的条件及方程组和不等式的解法.
∵ m2-(m2-3m)i<(m2-4m+3)i+10, 且虚数不能比较大小,
∴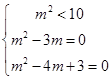 ,解得
,解得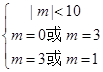 ,∴ m=3.
,∴ m=3.
当m=3时,原不等式成立.
诠释:本题应抓住复数能比较大小时必须都为实数这一条件。
例9.已知z=x+yi(x,y∈R),且 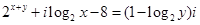 ,求z.
,求z.
解:本题主要考查复数相等的充要条件及指数方程,对数方程的解法.
∵ 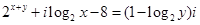 ,∴
,∴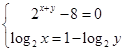 ,∴
,∴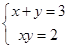 ,
,
解得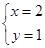 或
或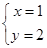 , ∴ z=2+i或z=1+2i.
, ∴ z=2+i或z=1+2i.
诠释:本题应抓住复数相等的充要条件这一关键,正确、熟练地解方程(指数,对数方程)
例10.已知x为纯虚数,y是实数,且2x-1+i=y-(3-y)i,求x、y的值.
解:本题主要考查复数的有关概念,实数与i的运算,复数相等的充要条件,方程组的解法.
设x=ti (t∈R,且t≠0),则2x-1+i=y-(3-y)i可化为
2ti-1+i=y-(3-y)i,即(2t+1)i-1=y-(3-y)i,
∴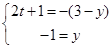 , ∴y=-1, t=-
, ∴y=-1, t=-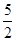 , ∴ x=-
, ∴ x=-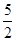 i.
i.
2.复数的四则运算
例1.计算:
(1)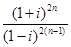 ,n∈N+;
,n∈N+;
(2)若ω=-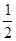 +
+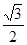 i,ω3=1,计算
i,ω3=1,计算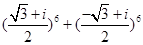 ;
;
(3)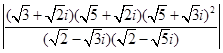 ;
;
(4)S=1+2i+3i2+4i3+……+100i99.
解:(1)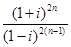 =
=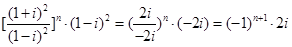
=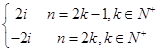 .
.
(2)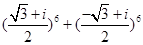 =
=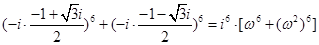
=-2.
(3)由于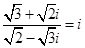 ,
, 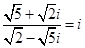 ,
,
∴ 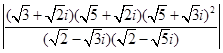 =
=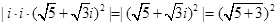
=8.
(4)S=1+2i+3i2+4i3+……+100i99
=(1+2i+3i2+4i3)+(5i4+6i5+7i6+8i7)+……+(97i96+98i97+99i98+100i99)
=(1+2i-3-4i)+(5+6i-7-8i)+……+(97+98i-99-100i)
=25(-2-2i)=-50-50i.
例2.已知复数z满足|z-2|=2,z+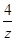 ∈R,求z.
∈R,求z.
解:设z=x+yi, x, y∈R,则
z+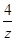 =z+
=z+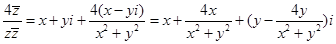 ,
,
∵ z+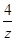 ∈R,∴
∈R,∴ 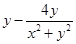 =0, 又|z-2|=2, ∴ (x-2)2+y2=4,
=0, 又|z-2|=2, ∴ (x-2)2+y2=4,
联立解得,当y=0时, x=4或x=0 (舍去x=0, 因此时z=0),
当y≠0时, 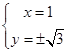 , z=1±
, z=1±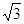 ,
,
∴ 综上所得 z1=4,z2=1+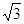 i,z3=1-
i,z3=1-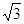 i.
i.
例3.设z为虚数,求证:z+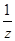 为实数的充要条件是|z|=1.
为实数的充要条件是|z|=1.
证明:设z=a+bi (a, b∈R,b≠0),于是
z+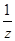 =(a+bi)+
=(a+bi)+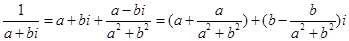 ,
,
所以b≠0, (z+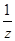 )∈R
)∈R b-
b-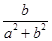 =0
=0 a2+b2=1
a2+b2=1 |z|=1.
|z|=1.
例4.复数z满足(z+1)(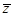 +1)=|
+1)=|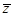 |2,且
|2,且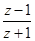 为纯虚数,求z.
为纯虚数,求z.
解:设z=x+yi (x, y∈R),则
(z+1)(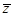 +1)=|
+1)=|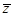 |2+z+
|2+z+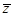 +1=|
+1=|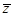 |2,∴ z+
|2,∴ z+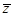 +1=0,z+
+1=0,z+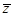 =-1,x=-
=-1,x=-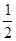 .
.
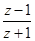 =
=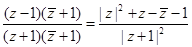 =
=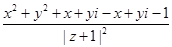 为纯虚数,
为纯虚数,
∴ x2+y2-1=0, y=±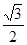 , ∴ z=-
, ∴ z=-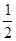 +
+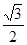 i或z=-
i或z=-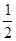 -
-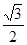 i.
i.
例5.复数z满足(1+2i)z+(3-10i)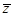 =4-34i,求z.
=4-34i,求z.
解:设z=x+yi (x, y∈R),则(1+2i)(x+yi)+(3-10i)(x-yi) =4-34i,
整理得(4x-12y)-(8x+2y)i=4-34i.
∴ 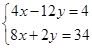 , 解得
, 解得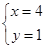 , ∴ z=4+i.
, ∴ z=4+i.
例6.设z是虚数,ω=z+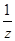 是实数,且-1<ω<2,
是实数,且-1<ω<2,
(1)求|z|的值及z的实部的取值范围;(2)设u=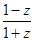 ,求证u为 纯虚数;
,求证u为 纯虚数;
(3)求ω-u2的最小值。
解:(1)设z=a+bi (a, b∈R, b≠0),则
ω=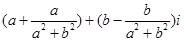 ,由于ω是实数且b≠0,∴ a2+b2=1,
,由于ω是实数且b≠0,∴ a2+b2=1,
即|z|=1,由ω=2a, -1<ω<2, ∴ z的实部a的的取值范围是(-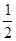 , 1).
, 1).
(2)u=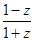 =
= ,由于a∈(-
,由于a∈(-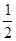 , 1), b≠0,
, 1), b≠0,
∴ u是纯虚数。
(3)ω-u2=2a+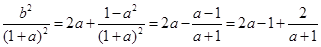
=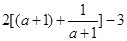 ,
,
由于a∈(-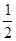 , 1),∴ a+1>0,则ω-u2≥2×2-3=1,
, 1),∴ a+1>0,则ω-u2≥2×2-3=1,
当a+1=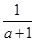 , 即a=0时,上式取等号,所以ω-u2的最小值为1.
, 即a=0时,上式取等号,所以ω-u2的最小值为1.
例7.证明: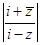 =1.
=1.
解:此题考查复数的运算、模的定义,共轭复数的性质等.
设z=a+bi,(a, b∈R),则
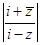 =
=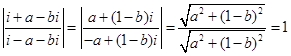 .
.
解2:∵ 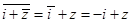 ,∴
,∴ 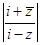 =
=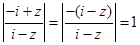 .
.
诠释:此题抓住模的定义或共轭复数的性质来求解.
例8.(20##年高考)已知复数z=1+i,求实数a,b使az+2b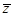 =(a+2z)2.
=(a+2z)2.
解:此题主要考查共轭复数,复数的四则运算,复数的相等.
∵ z=1+i,∴az+2b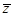 =(a+2b)+(a-2b)i,
=(a+2b)+(a-2b)i,
(a+2z)2=(a+2)2-4+4(a+2)i=(a2+4a)+4(a+2)i.
∴ 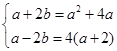 ,解得
,解得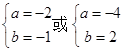 .
.
例9.若复数z满足z=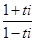 (t∈R),求z的对应点Z的轨迹方程.
(t∈R),求z的对应点Z的轨迹方程.
解:此题主要考查复数的四则运算,点的轨迹方程的求法等.
设z=x+yi,(x, y∈R),∵ z=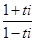 =
=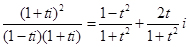 ,
,
∴ 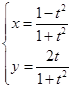 ,消去参数 t,得x2+y2= 1,且x≠-1.
,消去参数 t,得x2+y2= 1,且x≠-1.
∴ 所求方程为x2+y2=1(x≠-1).
诠释:解此题应抓住复数相等的充要条件,从而得到参数方程,消去参数,或者利用模的定义和性质,求出|z|即可.
例10.已知复数z满足|z|=5,且(3+ 4i)z是纯虚数,求z.
解:此题主要考查复数的有关概念,复数的运算,模的定义及计算.
设 z=x+yi(x, y∈R), ∵|z|=5,
∴x2+y2=25, 又(3+4i)z=(3+4i)(x+yi)=(3x-4y)+(4x+3y)i是纯虚数,
∴ 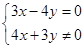 , 联立三个关系式解得
, 联立三个关系式解得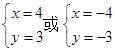 ,
,
∴ z=4+3i或z=-4-3i.
诠释:解此题应抓住纯虚数的定义和模的定义而得到方程组,正确解方程组即可.
例11.设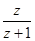 是纯虚数,求复数z对应的点的轨迹方程.
是纯虚数,求复数z对应的点的轨迹方程.
解:此题主要考查复数的有关概念及性质,四则运算和点的轨迹方程的求法.
∵ 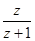 是纯虚数,∴
是纯虚数,∴ 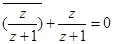 ,即
,即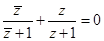 ,
,
∴ 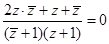 ,∴ 2z
,∴ 2z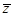 +z+
+z+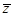 =0,(z≠0,z≠-1),
=0,(z≠0,z≠-1),
设z=x+yi,(x,y∈R),2(x2+y2)+2x=0(y≠0)
∴ (x+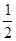 )2+y2=
)2+y2=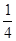 (y≠0).它为复数z对应点的轨迹方程.
(y≠0).它为复数z对应点的轨迹方程.
诠释:解此题应抓住虚数的定义和共扼复数的性质,利用运算法则进行求解。
