百时教育
解排列组合应用题的21种策略
排列组合问题是高考的必考题,它联系实际生动有趣,但题型多样,思路灵活,不易掌握,实践证明,掌握题型和解题方法,识别模式,熟练运用,是解决排列组合应用题的有效途径;下面就谈一谈排列组合应用题的解题策略.
1.相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列.
例1.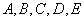 五人并排站成一排,如果
五人并排站成一排,如果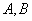 必须相邻且
必须相邻且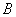 在
在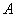 的右边,那么不同的排法种数有( )
的右边,那么不同的排法种数有( )
A、60种 B、48种 C、36种 D、24种
解析:把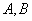 视为一人,且
视为一人,且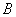 固定在
固定在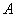 的右边,则本题相当于4人的全排列,
的右边,则本题相当于4人的全排列,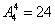 种,答案:
种,答案: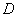 .
.
2.相离问题插空排:元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端.
例2.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是( )
A、1440种 B、3600种 C、4820种 D、4800种
解析:除甲乙外,其余5个排列数为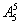 种,再用甲乙去插6个空位有
种,再用甲乙去插6个空位有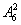 种,不同的排法种数是
种,不同的排法种数是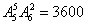 种,选
种,选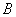 .
.
3.定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序,可用缩小倍数的方法.
例3.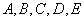 五人并排站成一排,如果
五人并排站成一排,如果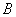 必须站在
必须站在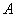 的右边(
的右边(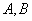 可以不相邻)那么不同的排法种数
可以不相邻)那么不同的排法种数
是( )
A、24种 B、60种 C、90种 D、120种
解析: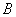 在
在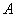 的右边与
的右边与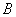 在
在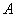 的左边排法数相同,所以题设的排法只是5个元素全排列数的一半,即
的左边排法数相同,所以题设的排法只是5个元素全排列数的一半,即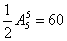 种,选
种,选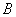 .
.
4.标号排位问题分步法:把元素排到指定位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成.
例4.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有( )
A、6种 B、9种 C、11种 D、23种
解析:先把1填入方格中,符合条件的有3种方法,第二步把被填入方格的对应数字填入其它三个方格,又有三种方法;第三步填余下的两个数字,只有一种填法,共有3×3×1=9种填法,选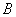 .
.
5.有序分配问题逐分法:有序分配问题指把元素分成若干组,可用逐步下量分组法.
例5.(1)有甲乙丙三项任务,甲需2人承担,乙丙各需一人承担,从10人中选出4人承担这三项任务,不同的选法种数是( )
A、1260种 B、2025种 C、2520种 D、5040种
解析:先从10人中选出2人承担甲项任务,再从剩下的8人中选1人承担乙项任务,第三步从另外的7人中选1人承担丙项任务,不同的选法共有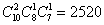 种,选
种,选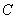 .
.
(2)12名同学分别到三个不同的路口进行流量的调查,若每个路口4人,则不同的分配方案有( )
A、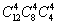 种 B、
种 B、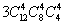 种 C、
种 C、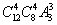 种 D、
种 D、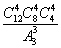 种
种
答案: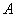 .
.
6.全员分配问题分组法:
例6.(1)4名优秀学生全部保送到3所学校去,每所学校至少去一名,则不同的保送方案有多少种?
解析:把四名学生分成3组有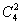 种方法,再把三组学生分配到三所学校有
种方法,再把三组学生分配到三所学校有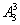 种,故共有
种,故共有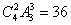 种方法.
种方法.
说明:分配的元素多于对象且每一对象都有元素分配时常用先分组再分配.
(2)5本不同的书,全部分给4个学生,每个学生至少一本,不同的分法种数为( )
A、480种 B、240种 C、120种 D、96种
答案: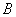 .
.
7.名额分配问题隔板法:
例7:10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案?
解析:10个名额分到7个班级,就是把10个名额看成10个相同的小球分成7堆,每堆至少一个,可以在10个小球的9个空位中插入6块木板,每一种插法对应着一种分配方案,故共有不同的分配方案为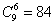 种.
种.
8.限制条件的分配问题分类法:
例8.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?
解析:因为甲乙有限制条件,所以按照是否含有甲乙来分类,有以下四种情况:
①若甲乙都不参加,则有派遣方案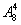 种;②若甲参加而乙不参加,先安排甲有3种方法,然后安排其余学生有
种;②若甲参加而乙不参加,先安排甲有3种方法,然后安排其余学生有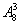 方法,所以共有
方法,所以共有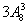 ;③若乙参加而甲不参加同理也有
;③若乙参加而甲不参加同理也有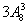 种;④若甲乙都参加,则先安排甲乙,有7种方法,然后再安排其余8人到另外两个城市有
种;④若甲乙都参加,则先安排甲乙,有7种方法,然后再安排其余8人到另外两个城市有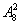 种,共有
种,共有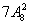 方法.所以共有不同的派遣方法总数为
方法.所以共有不同的派遣方法总数为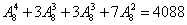 种.
种.
9.多元问题分类法:元素多,取出的情况也多种,可按结果要求分成不相容的几类情况分别计数,最后总计.
例9(1)由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A、210种 B、300种 C、464种 D、600种
解析:按题意,个位数字只可能是0,1,2,3,4共5种情况,分别有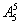 个,
个,
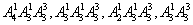 个,合并总计300个,选
个,合并总计300个,选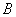 .
.
(2)从1,2,3…,100这100个数中,任取两个数,使它们的乘积能被7整除,这两个数的取法(不计顺序)共有多少种?
解析:被取的两个数中至少有一个能被7整除时,他们的乘积就能被7整除,将这100个数组成的集合视为全集I,能被7整除的数的集合记做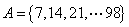 共有14个元素,不能被7整除的数组成的集合记做
共有14个元素,不能被7整除的数组成的集合记做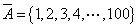 共有86个元素;由此可知,从
共有86个元素;由此可知,从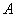 中任取2个元素的取法有
中任取2个元素的取法有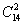 ,从
,从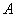 中任取一个,又从
中任取一个,又从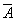 中任取一个共有
中任取一个共有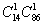 ,两种情形共符合要求的取法有
,两种情形共符合要求的取法有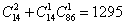 种.
种.
(3)从1,2,3,…,100这100个数中任取两个数,使其和能被4整除的取法(不计顺序)有多少种?
解析:将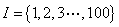 分成四个不相交的子集,能被4整除的数集
分成四个不相交的子集,能被4整除的数集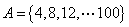 ;能被4除余1的数集
;能被4除余1的数集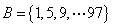 ,能被4除余2的数集
,能被4除余2的数集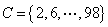 ,能被4除余3的数集
,能被4除余3的数集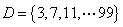 ,易见这四个集合中每一个有25个元素;从
,易见这四个集合中每一个有25个元素;从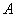 中任取两个数符合要;从
中任取两个数符合要;从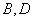 中各取一个数也符合要求;从
中各取一个数也符合要求;从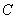 中任取两个数也符合要求;此外其它取法都不符合要求;所以符合要求的取法共有
中任取两个数也符合要求;此外其它取法都不符合要求;所以符合要求的取法共有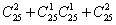 种.
种.
10.交叉问题集合法:某些排列组合问题几部分之间有交集,可用集合中求元素个数公式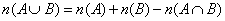 .
.
例10.从6名运动员中选出4人参加4×100米接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同的参赛方案?
解析:设全集={6人中任取4人参赛的排列},A={甲跑第一棒的排列},B={乙跑第四棒的排列},根据求集合元素个数的公式得参赛方法共有:
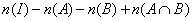
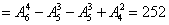 种.
种.
11.定位问题优先法:某个或几个元素要排在指定位置,可先排这个或几个元素;再排其它的元素。
例11.1名老师和4名获奖同学排成一排照相留念,若老师不站两端则有不同的排法有多少种?
解析:老师在中间三个位置上选一个有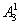 种,4名同学在其余4个位置上有
种,4名同学在其余4个位置上有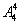 种方法;所以共有
种方法;所以共有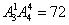 种。.
种。.
12.多排问题单排法:把元素排成几排的问题可归结为一排考虑,再分段处理。
例12.(1)6个不同的元素排成前后两排,每排3个元素,那么不同的排法种数是( )
A、36种 B、120种 C、720种 D、1440种
解析:前后两排可看成一排的两段,因此本题可看成6个不同的元素排成一排,共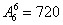 种,选
种,选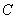 .
.
(2)8个不同的元素排成前后两排,每排4个元素,其中某2个元素要排在前排,某1个元素排在后排,有多少种不同排法?
解析:看成一排,某2个元素在前半段四个位置中选排2个,有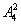 种,某1个元素排在后半段的四个位置中选一个有
种,某1个元素排在后半段的四个位置中选一个有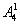 种,其余5个元素任排5个位置上有
种,其余5个元素任排5个位置上有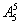 种,故共有
种,故共有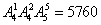 种排法.
种排法.
13.“至少”“至多”问题用间接排除法或分类法:
例13.从4台甲型和5台乙型电视机中任取3台,其中至少要甲型和乙 型电视机各一台,则不同的取法共有 ( )
A、140种 B、80种 C、70种 D、35种
解析1:逆向思考,至少各一台的反面就是分别只取一种型号,不取另一种型号的电视机,故不同的取法共有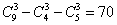 种,选.
种,选.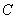
解析2:至少要甲型和乙 型电视机各一台可分两种情况:甲型1台乙型2台;甲型2台乙型1台;故不同的取法有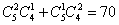 台,选
台,选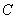 .
.
14.选排问题先取后排:从几类元素中取出符合题意的几个元素,再安排到一定的位置上,可用先取后排法.
例14.(1)四个不同球放入编号为1,2,3,4的四个盒中,则恰有一个空盒的放法有多少种?
解析:先取四个球中二个为一组,另二组各一个球的方法有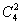 种,再排:在四个盒中每次排3个有
种,再排:在四个盒中每次排3个有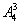 种,故共有
种,故共有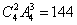 种.
种.
(2)9名乒乓球运动员,其中男5名,女4名,现在要进行混合双打训练,有多少种不同的分组方法?
解析:先取男女运动员各2名,有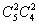 种,这四名运动员混和双打练习有
种,这四名运动员混和双打练习有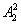 中排法,故共有
中排法,故共有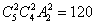 种.
种.
15.部分合条件问题排除法:在选取的总数中,只有一部分合条件,可以从总数中减去不符合条件数,即为所求.
例15.(1)以正方体的顶点为顶点的四面体共有( )
A、70种 B、64种 C、58种 D、52种
解析:正方体8个顶点从中每次取四点,理论上可构成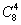 四面体,但6个表面和6个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有
四面体,但6个表面和6个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有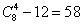 个.
个.
(2)四面体的顶点和各棱中点共10点,在其中取4个不共面的点,不同的取法共有( )
A、150种 B、147种 C、144种 D、141种
解析:10个点中任取4个点共有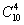 种,其中四点共面的有三种情况:①在四面体的四个面上,每面内四点共面的情况为
种,其中四点共面的有三种情况:①在四面体的四个面上,每面内四点共面的情况为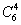 ,四个面共有
,四个面共有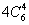 个;②过空间四边形各边中点的平行四边形共3个;③过棱上三点与对棱中点的三角形共6个.所以四点不共面的情况的种数是
个;②过空间四边形各边中点的平行四边形共3个;③过棱上三点与对棱中点的三角形共6个.所以四点不共面的情况的种数是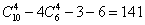 种.
种.
16.圆排问题单排法:把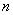 个不同元素放在圆周
个不同元素放在圆周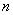 个无编号位置上的排列,顺序(例如按顺时钟)不同的排法才算不同的排列,而顺序相同(即旋转一下就可以重合)的排法认为是相同的,它与普通排列的区别在于只计顺序而首位、末位之分,下列
个无编号位置上的排列,顺序(例如按顺时钟)不同的排法才算不同的排列,而顺序相同(即旋转一下就可以重合)的排法认为是相同的,它与普通排列的区别在于只计顺序而首位、末位之分,下列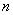 个普通排列:
个普通排列:
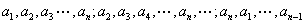 在圆排列中只算一种,因为旋转后可以重合,故认为相同,
在圆排列中只算一种,因为旋转后可以重合,故认为相同,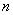 个元素的圆排列数有
个元素的圆排列数有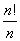 种.因此可将某个元素固定展成单排,其它的
种.因此可将某个元素固定展成单排,其它的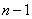 元素全排列.
元素全排列.
例16.5对姐妹站成一圈,要求每对姐妹相邻,有多少种不同站法?
解析:首先可让5位姐姐站成一圈,属圆排列有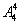 种,然后在让插入其间,每位均可插入其姐姐的左边和右边,有2种方式,故不同的安排方式
种,然后在让插入其间,每位均可插入其姐姐的左边和右边,有2种方式,故不同的安排方式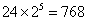 种不同站法.
种不同站法.
说明:从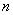 个不同元素中取出
个不同元素中取出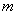 个元素作圆形排列共有
个元素作圆形排列共有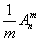 种不同排法.
种不同排法.
17.可重复的排列求幂法:允许重复排列问题的特点是以元素为研究对象,元素不受位置的约束,可逐一安排元素的位置,一般地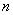 个不同元素排在
个不同元素排在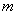 个不同位置的排列数有
个不同位置的排列数有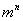 种方法.
种方法.
例17.把6名实习生分配到7个车间实习共有多少种不同方法?
解析:完成此事共分6步,第一步;将第一名实习生分配到车间有7种不同方案,第二步:将第二名实习生分配到车间也有7种不同方案,依次类推,由分步计数原理知共有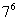 种不同方案.
种不同方案.
18.复杂排列组合问题构造模型法:
例18.马路上有编号为1,2,3…,9九只路灯,现要关掉其中的三盏,但不能关掉相邻的二盏或三盏,也不能关掉两端的两盏,求满足条件的关灯方案有多少种?
解析:把此问题当作一个排对模型,在6盏亮灯的5个空隙中插入3盏不亮的灯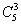 种方法,所以满足条件的关灯方案有10种.
种方法,所以满足条件的关灯方案有10种.
说明:一些不易理解的排列组合题,如果能转化为熟悉的模型如填空模型,排队模型,装盒模型可使问题容易解决.
19.元素个数较少的排列组合问题可以考虑枚举法:
例19.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的盒子现将这5个球投入5个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?
解析:从5个球中取出2个与盒子对号有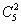 种,还剩下3个球与3个盒子序号不能对应,利用枚举法分析,如果剩下3,4,5号球与3,4,5号盒子时,3号球不能装入3号盒子,当3号球装入4号盒子时,4,5号球只有1种装法,3号球装入5号盒子时,4,5号球也只有1种装法,所以剩下三球只有2种装法,因此总共装法数为
种,还剩下3个球与3个盒子序号不能对应,利用枚举法分析,如果剩下3,4,5号球与3,4,5号盒子时,3号球不能装入3号盒子,当3号球装入4号盒子时,4,5号球只有1种装法,3号球装入5号盒子时,4,5号球也只有1种装法,所以剩下三球只有2种装法,因此总共装法数为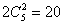 种.
种.
20.复杂的排列组合问题也可用分解与合成法:
例20.(1)30030能被多少个不同偶数整除?
解析:先把30030分解成质因数的形式:30030=2×3×5×7×11×13;依题意偶因数2必取,3,5,7,11,13这5个因数中任取若干个组成成积,所有的偶因数为
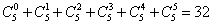 个.
个.
(2)正方体8个顶点可连成多少队异面直线?
解析:因为四面体中仅有3对异面直线,可将问题分解成正方体的8个顶点可构成多少个不同的四面体,从正方体8个顶点中任取四个顶点构成的四面体有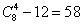 个,所以8个顶点可连成的异面直线有3×58=174对.
个,所以8个顶点可连成的异面直线有3×58=174对.
21.利用对应思想转化法:对应思想是教材中渗透的一种重要的解题方法,它可以将复杂的问题转化为简单问题处理.
例21.(1)圆周上有10点,以这些点为端点的弦相交于圆内的交点有多少个?
解析:因为圆的一个内接四边形的两条对角线相交于圆内一点,一个圆的内接四边形就对应着两条弦相交于圆内的一个交点,于是问题就转化为圆周上的10个点可以确定多少个不同的四边形,显然有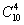 个,所以圆周上有10点,以这些点为端点的弦相交于圆内的交点有
个,所以圆周上有10点,以这些点为端点的弦相交于圆内的交点有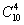 个.
个.
(2)某城市的街区有12个全等的矩形组成,其中实线表示马路,从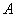 到
到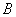 的最短路径有多少种?
的最短路径有多少种?
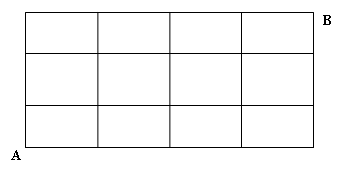
解析:可将图中矩形的一边叫一小段,从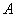 到
到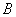 最短路线必须走7小段,其中:向东4段,向北3段;而且前一段的尾接后一段的首,所以只要确定向东走过4段的走法,便能确定路径,因此不同走法有
最短路线必须走7小段,其中:向东4段,向北3段;而且前一段的尾接后一段的首,所以只要确定向东走过4段的走法,便能确定路径,因此不同走法有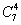 种.
种.
第二篇:排列组合问题的解题策略
排列组合问题的解题策略
樊晓春 甘肃省泾川县高平中学 744306
摘要:排列组合问题的解法有特殊元素优先法,相邻问题捆绑法,不相邻问题插空法,正难问题排除法,多元问题合理分类与准确分步,定序问题除法,大小排列问题字典法,名额分配问题隔板法,复杂问题转换法。 关键字:排列、组合、解题策略
排列组合问题是历年高考必考的内容,题目设置在选择或填空题,虽然分值少,但是也是容易失分的题,下面就简单的介绍几种排列组合问题的解法。
1.特殊元素——优先法:
对于含有限定条件的排列、组合问题,一般应先考虑特殊元素,再考虑其它元素。
例1.用0、2、3、4、5这五个数字,组成没有重复数字的三位数,其中偶数共有多少个?
[解析]因组成的三位数为偶数,末尾的数字必须是偶数,又0不能排在首位,故0是其中的特殊元素应优先安排。①当0排在末尾时,有A4个;②当0不排在
111末尾时,有A2个,根据分类计数原理,其中偶数共有30个。 ?A3?A32
例2.1名老师和4名获奖学生排成一排照相留念,若老师不排在两端,则共有不同的排法多少种?
[解析]优先考虑对特殊元素(老师)的排法,因老师不排在两端,故可在中间三个位置上来排,有3种。剩下的位置由4名学生全排列,有A4种。因此共有3A4?72种不同的排法。
2.相邻问题——捆绑法:
对于某几个元素要求相邻的排列问题,可先将相邻的元素“捆绑”在一起看作一个元素与其它元素进行排列,然后再对这几个元素进行全排列。 例3.5名学生和3名老师站成一排照相,3名老师必须站在一起的不同排法共有 种。
[解析]将3名老师捆绑起来看成一个元素,与5名学生排列,有A6种排法;而3名老师之间又有A3种排法,故满足条件的排法共有A6A3?726种。 例4.计划展出10幅不同的画,其中一幅水彩画,4幅油画,5幅国画,排成364463
一行陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端,那么不同的陈列方式有多少种?
[解析]把每种画捆绑在一起,看成一个整体,又水彩画较特殊,应优先安排。水彩画放中间,油画和国画放两端有A2种排法。再考虑油画和国画本身可
245全排列,故排列方法共有A2A4A5种。 2
3.不相邻问题——插空法:
对于某几个元素要求不相邻的排列问题,可先将余下的元素进行排列,然后在这些元素形成的空隙中将不相邻的元素进行排列。
例5.有10个学生,其中4人中任意两个不能站在一起,有多少种排列次序?
[解析]先将其余6人进行排列,有A6种;再把不相邻的4人分别排在前6人
64形成的7个空隙中,有A7种。所以共有A6种排列次序。 ?A746
例6.有4名男生,3名女生站成一排,任何两名女生彼此不相邻,有多少不同的排法?
[解析]由于要求女生不相邻,应先排男生,有A4种;然后在男生形成的5个空隙中分别安排3名女生,有A5种,所以共有A4?A5种。
4.正难问题——排除法:
对某些排列组合问题,当从正面入手情况复杂,不易解决时,可考虑从反面入手,将其等价转换为一个较简单的问题来处理。
例7.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有
A、 140种 B、120种 C、 35种 D、 34种
[解析]本题只要选出四个人就行,所以只选而不排,是组合问题,先不考虑附加条件,从7名学生中选出4名共有C7种选法,其中不符合条件的是选出的4人都是男生,即C4=1种。所以符合条件的选法是34种,故选D。
例8.四面体的顶点和各棱的中点共10个点,在其中取4个不共面的点,不同的取法共有
A、150种 B、147种 C、144种 D、141种
[解析]首先只要考虑从10个点中任取4个点的取法,有C10种,然后再取掉“共面”的情况:其中一个面内的6个点中任意4点都共面,任取4点有4?C6种;44443434
又每条棱上三点与相对棱的中点共面共有6种;各棱的中点中4点共面的有3种。
44故10个点中4点不共面的取法,共有C10?4?C6?6?3?141种。故选D项。
5.多元问题——合理分类与准确分步:
对于约束条件较多的排列组合问题,可能的情况也较多,可根据结果要求,按元素性质进行分类,按时间发生的连续过程分步,做到分类标准明确、分布层次清楚,不重不漏的原则。
例9.平面上4条平行直线与另5条平行直线互相垂直,则它们构成的矩形共有 个
[解析]按构成矩形的过程可分为如下两步:第一步,先在4条平行直线中取两条,有C4种;第二步,再在5条平行线中取两条,有C5种,这样取出的4条
22直线构成一个矩形。根据乘法原理,构成的矩形共有C4?C5?60个。 22
6.定序问题——除法:
对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一同排列,然后用总排列数除以这几个数的全排列数。(如有n个元素,其中m个元
Ann素的顺序一定,则这个n个元素的排法有m种) Am
小于十位数的共有 例10.由数字0、1、2、3、4、5组成没有重复数字的六位数,其中个位数
A、 210种 B、300种 C、 464种 D、 600种
15 [解析]若不考虑附加条件,组成的六位数共有A5?A5?600个,而其中个位数与十位数的两种排法中只有一种符合要求,故符合要求的六位数共有15A5?A5?300个,故选B项。 2
7.大小排列问题——字典法:
对于数的大小顺序排列问题,可以采用“查字典”的方法,逐位依次确定。 例11.在由数字1、2、3、4、5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有
A、 56种 B、57种 C、58种 D、 60种
[解析]从高位向低位依次考虑,分3类:①当首位是2时,若千位是4、5,
1213则有A2?A2?4个;若千位?A3?12个;若千位是3,百位是4、5,则有A2
是3,百位是1,则只有一个数即23154,故当首位是2时,共有12+4+1=17个。②
13当首位是3时,有A4?24个。③当首位是4时,若千位是1、2,则有A2?A3?12
12个;若千位是3,百位是1、2,则有A2?A2?4个;若千位是3,百位是5,则4
只有一个数即43512,故当首位是4时,共有12+4+1=17个数。因此满足题意的数共有17+24+17=58个。故选C项。
例12.用0、1、2、3、4五个数组成无重复数字的四位数,若按从小到大排列,3204是第几个数?
[解析]从高位向低位依次考虑,分3类:①当千位是1、2时,有A2?A4?48
12个。②当千位是3时,若百位排0、1,有A2?A3?12个;若百位排2时,比320413
小的仅有3201一个。故比4304小的四位数共有48+12+1=61个,则3204是第62个。
8.名额分配问题——隔板法:
对某些复杂的排列问题,可通过构造相应的模型来处理。
例13.某校准备组建一个18人的足球队,这18人由高一年级10个班的学生组成,每个班级至少一人,名额分配方案共有多少种?
[解析]处理次类问题一般构造一个隔板模型。取18枚棋子排成一列,在相邻的每两枚棋子形成的17个空隙中选取9个插入隔板,将18个棋子分隔成10个部分,第i(1≤i≤10)个部分的棋子数对应第i个班级学生的名额,因此分配
9方案的种数与隔板的插入种数相等,即为C17种。
9.混合问题——先选后排法:
对于排列、组合的混合问题,可采取先选取元素,再进行排列的策略。 例14.12名同学合影,站成了前排除4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是( )
A、C8A3 B、C8A6 C、C8A6 D、C8A5
[解析]分步确定满足题意的调整方法数:第一步,从后排的8人中任选2人,有C8种不同的方法;第二步,将所选定的2人逐一插入前排,依次有5、6种不同的方法,即将所选定的两人插入前排共有有5?6?A6种方法,由分步计数原理可知,满足题意的不同调整方法种数是C8A6,选C项。
10.复杂问题——转换法: 222222262222
对于有些较为复杂的排列、组合问题,若不能用以上方法解决,可以采取等价转换的方法,转化为其它问题然后解决。
例15.从正方体的八个顶点中任取三个点作三角形,其中直角三角形的个数为( ) A、56 B、52 C、 48 D、 40
[解析]首先考虑到任意一个矩形可得到四个直角三角形,于是问题转化为先求出所有可能的矩形。分为两类:⑴表面上的矩形有6个;⑵对角面有6个,因此所有可能的矩形有6+6=12个,相应的直角三角形共有4 *12=48个。故选C项.
例16.一个口袋内有4个不同的红球,6个不同的白球,从中任取4个球,若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不小于7的取法有多少种?
[解析]设红球取x个,白球取5-x个,依题设有2x?(5?x)?7。其中x∈N, 则解得x?2、3、4,对应白球取3、2、1。故取法种数为
233241 C4C6?C4C6?C4C6?186种.
平凉工作站王国玉推荐
