 排列组合题型总结
排列组合题型总结
排列组合问题千变万化,解法灵活,条件隐晦,思维抽象,难以找到解题的突破口。因而在求解排列组合应用题时,除做到:排列组合分清,加乘原理辩明,避免重复遗漏外,还应注意积累排列组合问题得以快速准确求解。
一. 直接法
1.特殊元素法
例1用1,2,3,4,5,6这6个数字组成无重复的四位数,试求满足下列条件的四位数各有多少个
(1)数字1不排在个位和千位
(2)数字1不在个位,数字6不在千位。
分析:(1)个位和千位有5个数字可供选择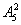 ,其余2位有四个可供选择
,其余2位有四个可供选择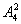 ,由乘法原理:
,由乘法原理: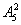
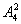 =240
=240
2.特殊位置法
(2)当1在千位时余下三位有 =60,1不在千位时,千位有
=60,1不在千位时,千位有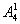 种选法,个位有
种选法,个位有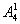 种,余下的有
种,余下的有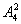 ,共有
,共有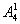
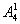
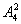 =192所以总共有192+60=252
=192所以总共有192+60=252
二. 间接法 当直接法求解类别比较大时,应采用间接法。如上例中(2)可用间接法
当直接法求解类别比较大时,应采用间接法。如上例中(2)可用间接法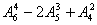 =252
=252
例2 有五张卡片,它的正反面分别写0与1,2与3,4与5,6与7,8与9,将它们任意三张并排放在一起组成三位数,共可组成多少个不同的三维书?
分析:此例正面求解需考虑0与1卡片用与不用,且用此卡片又分使用0与使用1,类别较复杂,因而可使用间接计算:任取三张卡片可以组成不同的三位数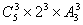 个,其中0在百位的有
个,其中0在百位的有
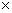
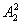 个,这是不合题意的。故共可组成不同的三位数
个,这是不合题意的。故共可组成不同的三位数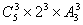 -
-
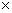
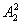 =432(个)
=432(个)
三. 插空法 当需排元素中有不能相邻的元素时,宜用插空法。
例3 在一个含有8个节目的节目单中,临时插入两个歌唱节目,且保持原节目顺序,有多少中插入方法?
分析:原有的8个节目中含有9个空档,插入一个节目后,空档变为10个,故有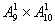 =100中插入方法。
=100中插入方法。
四. 捆绑法 当需排元素中有必须相邻的元素时,宜用捆绑法。
例4 4名男生和3名女生共坐一排,男生必须排在一起的坐法有多少种?
分析:先将男生捆绑在一起看成一个大元素与女生全排列有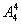 种排法,而男生之间又有
种排法,而男生之间又有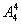 种排法,又乘法原理满足条件的排法有:
种排法,又乘法原理满足条件的排法有: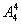 ×
×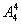 =576
=576
练习1.四个不同的小球全部放入三个不同的盒子中,若使每个盒子不空,则不同的放法有 种(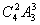 )
)
2. 某市植物园要在30天内接待20所学校的学生参观,但每天只能安排一所学校,其中有一所学校人数较多,要安排连续参观2天,其余只参观一天,则植物园30天内不同的安排方法有( )(注意连续参观2天,即需把30天种的连续两天捆绑看成一天作为一个整体来选有
)(注意连续参观2天,即需把30天种的连续两天捆绑看成一天作为一个整体来选有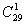 其余的就是19所学校选28天进行排列)
其余的就是19所学校选28天进行排列)
五. 阁板法 名额分配或相同物品的分配问题,适宜采阁板用法
例5 某校准备组建一个由12人组成篮球队,这12个人由8个班的学生组成,每班至少一人,名额分配方案共 种 。
分析:此例的实质是12个名额分配给8个班,每班至少一个名额,可在12个名额种的11个空当中插入7块闸板,一种插法对应一种名额的分配方式,故有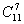 种
种
练习1.(a+b+c+d)15有多少项?
当项中只有一个字母时,有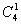 种(即a.b.c.d而指数只有15故
种(即a.b.c.d而指数只有15故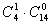 。
。
当项中有2个字母时,有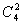 而指数和为15,即将15分配给2个字母时,如何分,闸板法一分为2,
而指数和为15,即将15分配给2个字母时,如何分,闸板法一分为2,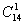 即
即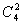
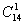
当项中有3个字母时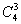 指数15分给3个字母分三组即可
指数15分给3个字母分三组即可
当项种4个字母都在时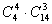 四者都相加即可.
四者都相加即可.
练习2.有20个不加区别的小球放入编号为1,2,3的三个盒子里,要求每个盒子内的球数不少编号数,问有多少种不同的方法?(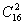 )
)
3.不定方程X1+X2+X3+…+X50=100中不同的整数解有(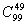 )
)
六. 平均分堆问题 例6 6本不同的书平均分成三堆,有多少种不同的方法?
分析:分出三堆书(a1,a2),(a3,a4),(a5,a6)由顺序不同可以有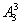 =6种,而这6种分法只算一种分堆方式,故6本不同的书平均分成三堆方式有
=6种,而这6种分法只算一种分堆方式,故6本不同的书平均分成三堆方式有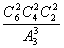 =15种
=15种
练习:1.6本书分三份,2份1本,1份4本,则有不同分法?
2.某年级6个班的数学课,分配给甲乙丙三名数学教师任教,每人教两个班,则分派方法的种数。
七. 合并单元格解决染色问题
例7 (全国卷(文、理))如图1,一个地区分为5个行政区域,现给地图着色,要求相邻区域不 得使用同一颜色,现有四种颜色可供选择,则不同的着色方法共有 种(以数字作答)。
分析:颜色相同的区域可能是2、3、4、5.
下面分情况讨论:
 (ⅰ)当2、4颜色相同且3、5颜色不同时,将2、4合并成一个单元格,此时不同的着色方法相当于4个元素 ①③⑤的全排列数
(ⅰ)当2、4颜色相同且3、5颜色不同时,将2、4合并成一个单元格,此时不同的着色方法相当于4个元素 ①③⑤的全排列数
(ⅱ)当2、4颜色不同且3、5颜色相同时,与情形(ⅰ)类似同理可得 种着色法.
种着色法.

 (ⅲ)当2、4与3、5分别同色时,将2、4;3、5分别合并,这样仅有三个单元格
(ⅲ)当2、4与3、5分别同色时,将2、4;3、5分别合并,这样仅有三个单元格
①
从4种颜色中选3种来着色这三个单元格,计有 种方法.
种方法.
由加法原理知:不同着色方法共有2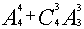 =48+24=72(种)
=48+24=72(种)
练习1(天津卷(文))将3种作物种植

在如图的5块试验田里,每快种植一种作物且相邻的试验田不能种植同一作物 ,
不同的种植方法共 种(以数字作答) (72)
2.(江苏、辽宁、天津卷(理))某城市中心广场建造一个花圃,花圃6分为个部分(如图3),现要栽种4种颜色的花,每部分栽种一种且相邻部分不能栽种 同一样颜色的话,不同的栽种方法有 种(以数字作答).(120)

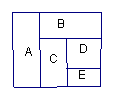
图3 图4
3.如图4,用不同的5种颜色分别为ABCDE五部分着色,相邻部分不能用同一颜色,但同一种颜色可以反复使用也可以不用,则符合这种要求的不同着色种数.(540)
 4.如图5:四个区域坐定4个单位的人,有四种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两区域的颜色不同,不相邻区域颜色相同,不相邻区域颜色相同与否不受限制,那么不同的着色方法是 种(84)
4.如图5:四个区域坐定4个单位的人,有四种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两区域的颜色不同,不相邻区域颜色相同,不相邻区域颜色相同与否不受限制,那么不同的着色方法是 种(84)
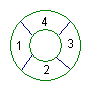
图5 图6
5.将一四棱锥(图6)的每个顶点染一种颜色,并使同一条棱的两端点异色,若只有五种颜色可供使用,则不同的染色方法共 种(420)
八. 递推法
例八 一楼梯共10级,如果规定每次只能跨上一级或两级,要走上这10级楼梯,共有多少种不同的走法?
分析:设上n级楼梯的走法为an种,易知a1=1,a2=2,当n≥2时,上n级楼梯的走法可分两类:第一类:是最后一步跨一级,有an-1种走法,第二类是最后一步跨两级,有an-2种走法,由加法原理知:an=an-1+ an-2,据此,a3=a1+a2=3,a4=a#+a2=5,a5=a4+a3=8,a6=13,a7=21,a8=34,a9=55,a10=89.故走上10级楼梯共有89种不同的方法。
九.几何问题
1.四面体的一个顶点位A,从其它顶点与各棱中点取3个点,使它们和点A在同一平面上,不同的取法有 种(3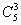 +3=33)
+3=33)
2.四面体的棱中点和顶点共10个点(1)从中任取3个点确定一个平面,共能确定多少个平面?
(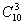 -4
-4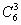 +4-3
+4-3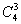 +3-6C
+3-6C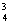 +6+2×6=29)
+6+2×6=29)
(2)以这10个点为顶点,共能确定多少格凸棱锥? 三棱锥 C104-4C64-6C44-3C44=141 四棱锥 6×4×4=96 3×6=18 共有114
十.先选后排法
例9 有甲乙丙三项任务,甲需2人承担,乙丙各需1人承担,从10人中选派4人承担这三项任务,不同的选派方法有( )
A.1260种 B.2025种 C.2520种 D.5054种
分析:先从10人中选出2人
十一.用转换法解排列组合问题
例10.某人连续射击8次有四次命中,其中有三次连续命中,按“中”与“不中”报告结果,不同的结果有多少种.
解 把问题转化为四个相同的黑球与四个相同白球,其中只有三个黑球相邻的排列问题.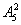 =20种
=20种
例11.个人参加秋游带10瓶饮料,每人至少带1瓶,一共有多少钟不同的带法.
解 把问题转化为5个相同的白球不相邻地插入已经排好的10个相同的黑球之间的9个空隙种的排列问题.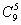 =126种
=126种
例12 从1,2,3,…,1000个自然数中任取10个不连续的自然数,有多少种不同的去法.
解 把稳体转化为10个相同的黑球与990个相同白球,其其中黑球不相邻的排列问题。
例13 某城市街道呈棋盘形,南北向大街5条,东西向大街4条,一人欲从西南角走到东北角,路程最短的走法有多少种.
解 无论怎样走必须经过三横四纵,因此,把问题转化为3个相同的白球与四个相同的黑球的排列问题.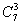 =35(种)
=35(种)
例14 一个楼梯共18个台阶12步登完,可一步登一个台阶也可一步登两个台阶,一共有多少种不同的走法.
解 根据题意要想12步登完只能6个一步登一个台阶,6个一步登两个台阶,因此,把问题转化为6个相同的黑球与6个相同的白球的排列问题.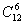 =924(种).
=924(种).
例15 求(a+b+c)10的展开式的项数.
解 展开使的项为aαbβcγ,且α+β+γ=10,因此,把问题转化为2个相同的黑球与10个相同的白球的排列问题.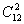 =66(种)
=66(种)
例16 亚、欧乒乓球对抗赛,各队均有5名队员,按事先排好的顺序参加擂台赛,双方先由1号队员比赛,负者淘汰,胜者再与负方2号队员比赛,直到一方全被淘汰为止,另一方获胜,形成一种比赛过程.那么所有可能出现的比赛过程有多少种?
解 设亚洲队队员为a1,a2,…,a5,欧洲队队员为b1,b2,…,b5,下标表示事先排列的出场顺序,若以依次被淘汰的队员为顺序.比赛过程转化为这10个字母互相穿插的一个排列,最后师胜队种步被淘汰的队员和可能未参加参赛的队员,所以比赛过程可表示为5个相同的白球和5个相同黑球排列问题,比赛过程的总数为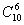 =252(种)
=252(种)
十二.转化命题法
例17圆周上共有15个不同的点,过其中任意两点连一弦,这些弦在圆内的交点最多有多少各?
分析:因两弦在圆内若有一交点,则该交点对应于一个以两弦的四端点为顶点的圆内接四边形,则问题化为圆周上的15个不同的点能构成多少个圆内接四边形,因此这些现在圆内的交点最多有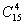 =1365(个)
=1365(个)
十三.概率法
例18一天的课程表要排入语文、数学、物理、化学、英语、体育六节课,如果数学必须排在体育之前,那么该天的课程表有多少种排法?
分析:在六节课的排列总数中,体育课排在数学之前与数学课排在体育之前的概率相等,均为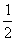 ,故本例所求的排法种数就是所有排法的
,故本例所求的排法种数就是所有排法的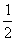 ,即
,即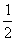 A=360种
A=360种
十四.除序法 例19 用1,2,3,4,5,6,7这七个数字组成没有重复数字的七位数中,
(1)若偶数2,4,6次序一定,有多少个?
(2)若偶数2,4,6次序一定,奇数1,3,5,7的次序也一定的有多少个?
解(1)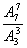 (2)
(2)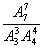
十五.错位排列
例20 同室四人各写一张贺卡,先集中起来,然后每人从中拿一张别人送出的卡片,则不同的分配方法有 种(9)
公式 1)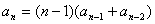 n=4时a4=3(a3+a2)=9种 即三个人有两种错排,两个人有一种错排.
n=4时a4=3(a3+a2)=9种 即三个人有两种错排,两个人有一种错排.
2)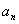 =n!(1-
=n!(1- +
+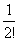 -
-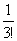 +…+
+…+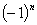

练习 有五位客人参加宴会,他们把帽子放在衣帽寄放室内,宴会结束后每人戴了一顶帽子回家,回家后,他们的妻子都发现他们戴了别人的帽子,问5位客人都不戴自己帽子的戴法有多少种?(44)
排列与组合的区别
排列与组合的共同点是从n个不同的元素中,任取m(m≤n)个元素,而不同点是排列是按照一定的顺序排成一列,组合是无论怎样的顺序并成一组,因此“有序”与“无序”是区别排列与组合的重要标志.下面通过实例来体会排列与组合的区别.
【例题】 判断下列问题是排列问题还是组合问题?并计算出种数.
(1) 高二年级学生会有11人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手?
(2) 高二数学课外活动小组共10人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选2名参加省数学竞赛,有多少种不同的选法?
(3) 有2、3、5、7、11、13、17、19八个质数:①从中任取两个数求它们的商,可以有多少个不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
(4) 有8盆花:①从中选出2盆分别给甲、乙两人每人一盆,有多少种不同的选法?②从中选出2盆放在教室有多少种不同的选法?
【思考与分析】 (1) ①由于每两人互通一封信,甲给乙的信与乙给甲的信是不同的两封信,所以与顺序有关,是排列;②由于每两人互握一次手,甲与乙握手、乙与甲握手是同一次握手,与顺序无关,所以是组合问题.其他类似分析.
解: (1) ①是排列问题,共通了=110(封);②是组合问题,共需握手==55(次)
(2) ①是排列问题,共有=10×9=90(种)不同的选法;②是组合问题,共=45(种)不同的选法;
(3) ①是排列问题,共有=8×7=56(个)不同的商;②是组合问题,共有=28(个)不同的积;
(4) ①是排列问题,共有=56(种)不同的选法;②是组合问题,共有=28(种)不同的选法. ( 【反思】 区分排列与组合的关键是“有序”与“无序”。 )
第二篇:丛文龙版排列组合题型总结 站在巨人的肩膀上,稍作整理
 排列组合题型总结
排列组合题型总结
排列组合问题千变万化,解法灵活,条件隐晦,思维抽象,难以找到解题的突破口。因而在求解排列组合应用题时,除做到:排列组合分清,加乘原理辩明,避免重复遗漏外,还应注意积累排列组合问题得以快速准确求解。站在巨人的肩膀上,稍作整理。
一. 直接法、
1. 特殊元素法
例1用1,2,3,4,5,6这6个数字组成无重复的四位数,试求满足下列条件的四位数各有多少个
(1)数字1不排在个位和千位
(2)数字1不在个位,数字6不在千位。
分析:(1)个位和千位有5个数字可供选择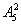 ,其余2位有四个可供选择
,其余2位有四个可供选择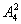 ,由乘法原理:
,由乘法原理: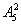
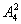 =240
=240
2.特殊位置法
(2)当1在千位时余下三位有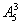 =60,1不在千位时,千位有
=60,1不在千位时,千位有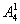 种选法,个位有
种选法,个位有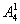 种,余下的有
种,余下的有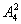 ,共有
,共有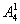
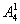
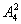 =192所以总共有192+60=252
=192所以总共有192+60=252
练习9.由0,1,2,3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是( )
A.24个 B.12个 C.6个 D.4个
16.(本题满分12分)用0,1,2,3,4,5这六个数字
(1) 可组成多少个不同的自然数? (2)可组成多少个无重复数字的五位数?
(3) 组成多少个无重复数字的五位奇数?
(4) 可组成多少个无重复数字的能被5整除的五位数?
(5) 可组成多少个无重复数字的且大于31250的五位数?
(6) 可组成多少个无重复数字的能被3整除的五位数?
解析:16.(1)解:可组成6+5 =46656个不同的自然数
=46656个不同的自然数
(2)可组成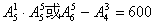 个无重复数字的五位数
个无重复数字的五位数
(3)可组成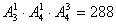 个无重复数字的五位奇数
个无重复数字的五位奇数
(4)可组成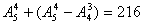 个无重复数字的能被5整除的五位数
个无重复数字的能被5整除的五位数
(5)可组成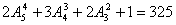 个无重复数字的且大于31250的五位数?
个无重复数字的且大于31250的五位数?
(6)可组成 个无重复数字的能被3整除的五位数?
个无重复数字的能被3整除的五位数?
间接法 当直接法求解类别比较大时,应采用间接法。如上例中(2)可用间接法
当直接法求解类别比较大时,应采用间接法。如上例中(2)可用间接法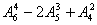 =252
=252
例2 有五张卡片,它的正反面分别写0与1,2与3,4与5,6与7,8与9,将它们任意三张并排放在一起组成三位数,共可组成多少个不同的三维书?
分析:此例正面求解需考虑0与1卡片用与不用,且用此卡片又分使用0与使用1,类别较复杂,因而可使用间接计算:任取三张卡片可以组成不同的三位数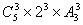 个,其中0在百位的有
个,其中0在百位的有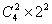
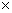
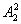 个,这是不合题意的。故共可组成不同的三位数
个,这是不合题意的。故共可组成不同的三位数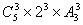 -
-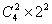
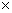
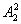 =432(个)
=432(个)
二.插空法 当需排元素中有不能相邻的元素时,宜用插空法。
例3 在一个含有8个节目的节目单中,临时插入两个歌唱节目,且保持原节目顺序,有多少中插入方法? 分析:原有的8个节目中含有9个空档,插入一个节目后,空档变为10个,故有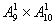 =100中插入方法。
=100中插入方法。
1.4名男歌手和2名女歌手联合举行一场音乐会,出场顺序要求两名女歌手之间恰有一名男歌手,共有出场方案的种数是 ( )A.6A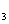
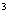 B.3A
B.3A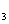
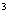 C.2A
C.2A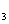
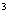 D.A
D.A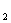
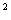 A
A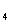
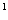 A
A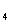
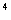
5.(北京理科第5题)记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( B )
A.1440种 B.960种 C.720种 D.480种
练习10、两男两女4个同学排成一列照相,如果要求男女相间而立,则满足条件的方法数共有(▲▲▲)
A.4种 B.8种 C.12种 D.6种 答案:B (注意)
三.捆绑法 当需排元素中有必须相邻的元素时,宜用捆绑法。
例4 4名男生和3名女生共坐一排,男生必须排在一起的坐法有多少种?
分析:先将男生捆绑在一起看成一个大元素与女生全排列有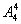 种排法,而男生之间又有
种排法,而男生之间又有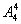 种排法,又乘法原理满足条件的排法有:
种排法,又乘法原理满足条件的排法有: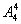 ×
×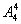 =576
=576
练习1.四个不同的小球全部放入三个不同的盒子中,若使每个盒子不空,则不同的放法有 种(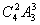 )
)
2. 某市植物园要在30天内接待20所学校的学生参观,但每天只能安排一所学校,其中有一所学校人数较多,要安排连续参观2天,其余只参观一天,则植物园30天内不同的安排方法有( )
)
(注意连续参观2天,即需把30天种的连续两天捆绑看成一天作为一个整体来选有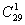 其余的就是19所学校选28天进行排列)
其余的就是19所学校选28天进行排列)
20.(12分)7名身高互不相等的学生,分别按下列要求排列,各有多少种不同的排法?
(1)7人站成一排,要求较高的3个学生站在一起;
(2)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减;
(3)任取6名学生,排成二排三列,使每一列的前排学生比后排学生矮.
20解:(1)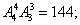 (2)
(2)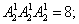 (3)
(3)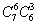
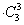 =140.
=140.
21.(12分)4位学生与2位教师并坐合影留念,针对下列各种坐法,试问:各有多少种不同的坐法?(1)教师必须坐在中间;(48)(2)教师不能坐在两端,但要坐在一起;144
(3)教师不能坐在两端,且不能相邻.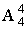
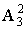
四.闸板法 名额分配或相同物品的分配问题,适宜采用闸办法
例5 某校准备组建一个由12人组成篮球队,这12个人由8个班的学生组成,每班至少一人,名额分配方案共 种 。
分析:此例的实质是12个名额分配给8个班,每班至少一个名额,可在12个名额种的11个空当中插入7块闸板,一种插法对应一种名额的分配方式,故有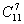 种
种
练习1.(a+b+c+d)15有多少项?
当项中只有一个字母时,有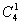 种(即a.b.c.d而指数只有15故
种(即a.b.c.d而指数只有15故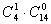 。
。
当项中有2个字母时,有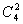 而指数和为15,即将15分配给2个字母时,如何分,闸板法一分为2,
而指数和为15,即将15分配给2个字母时,如何分,闸板法一分为2,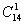 即
即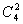
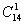
当项中有3个字母时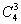 指数15分给3个字母分三组即可
指数15分给3个字母分三组即可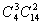
当项种4个字母都在时 四者都相加即可.
四者都相加即可.
3.不定方程X1+X2+X3+…+X50=100中不同的正整数解有(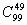 )
)
4.不定方程X1+X2+X3+…+X50=100中不同的自然数解有( )
练习2.有20个不加区别的小球放入编号为1,2,3的三个盒子里,要求每个盒子内的球数不少编号数,问有多少种不同的方法?(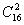 )
)
15、将7个不同的小球全部放入编号为2和3的两个盒子里,使得放入每个盒子里的球的个数不少于该盒子的编号,则不同的放球方法共有________种(用数字作答). 答案:91
五.平均分堆问题 例6 6本不同的书平均分成三堆,有多少种不同的方法?
分析:分出三堆书(a1,a2),(a3,a4),(a5,a6)由顺序不同可以有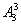 =6种,而这6种分法只算一种分堆方式,故6本不同的书平均分成三堆方式有
=6种,而这6种分法只算一种分堆方式,故6本不同的书平均分成三堆方式有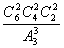 =15种
=15种
例24. 6本不同的书
(1) 分给甲乙丙三人,每人两本,有多少种不同的分法?
(2) 分成三堆,每堆两本,有多少种不同的分法?
(3) 分成三堆,一堆一本,一堆两本,一堆三本,有多少种不同的分法?
(4) 甲一本,乙两本,丙三本,有多少种不同的分法?
(5) 分给甲乙丙三人,其中一人一本,一人两本,第三人三本,有多少种不同的分法?
5.12名同学分别到三个不同的路口进行车流量的调查,若每个路口4人,则不同的分配
方案共有( )A.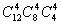 B.
B.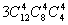 C.
C.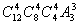 D.
D.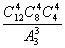
练习:1.6本书分三份,2份1本,1份4本,则有不同分法?
2.某年级6个班的数学课,分配给甲乙丙三名数学教师任教,每人教两个班,则分派方法的种数。
六. 合并单元格解决染色问题
 例7 (全国卷(文、理))如图1,一个地区分为5个行政区域,现给地图着色,要求相邻区域不 得使用同一颜色,现有四种颜色可供选择,则不同的着色方法共有 种(以数字作答)。分析:颜色相同的区域可能是2、3、4、5.
例7 (全国卷(文、理))如图1,一个地区分为5个行政区域,现给地图着色,要求相邻区域不 得使用同一颜色,现有四种颜色可供选择,则不同的着色方法共有 种(以数字作答)。分析:颜色相同的区域可能是2、3、4、5.
下面分情况讨论:
 (ⅰ)当2、4颜色相同且3、5颜色不同时,将2、4合并成一个单元格,此时不同的着色方法相当于4个元素 ①③⑤的全排列数
(ⅰ)当2、4颜色相同且3、5颜色不同时,将2、4合并成一个单元格,此时不同的着色方法相当于4个元素 ①③⑤的全排列数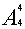
(ⅱ)当2、4颜色不同且3、5颜色相同时,与情形(ⅰ)类似同理可得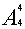 种着色法.
种着色法.

 (ⅲ)当2、4与3、5分别同色时,将2、4;3、5分别合并,这样仅有三个单元格
(ⅲ)当2、4与3、5分别同色时,将2、4;3、5分别合并,这样仅有三个单元格
①
从4种颜色中选3种来着色这三个单元格,计有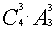 种方法.
种方法.
由加法原理知:不同着色方法共有2 =48+24=72(种)
=48+24=72(种)
练习1(天津卷(文))将3种作物种植

在如图的5块试验田里,每快种植一种作物且相邻的试验田不能种植同一作物 ,
不同的种植方法共 种(以数字作答) (72)
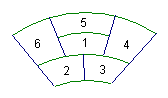
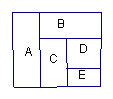 2.(江苏、辽宁、天津卷(理))某城市中心广场建造一个花圃,花圃6分为个部分(如图3),现要栽种4种颜色的花,每部分栽种一种且相邻部分不能栽种 同一样颜色的话,不同的栽种方法有 种(以数字作答).(120)
2.(江苏、辽宁、天津卷(理))某城市中心广场建造一个花圃,花圃6分为个部分(如图3),现要栽种4种颜色的花,每部分栽种一种且相邻部分不能栽种 同一样颜色的话,不同的栽种方法有 种(以数字作答).(120)
图3 图4
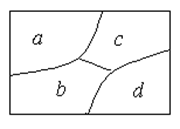
3.如图4,用不同的5种颜色分别为ABCDE五部分着色,相邻部分不能用同一颜色,但同一种颜色可以反复使用也可以不用,则符合这种要求的不同着色种数.(540)
 4.如图5:四个区域坐定4个单位的人,有四种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两区域的颜色不同,不相邻区域颜色相同,不相邻区域颜色相同与否不受限制,那么不同的着色方法是 种(84)
4.如图5:四个区域坐定4个单位的人,有四种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两区域的颜色不同,不相邻区域颜色相同,不相邻区域颜色相同与否不受限制,那么不同的着色方法是 种(84)
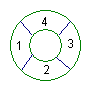
图5 图6 图7
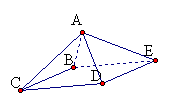
5.将一四棱锥(图6)的每个顶点染一种颜色,并使同一条棱的两端点异色,若只有五种颜色可供使用,则不同的染色方法共 种(420)
19.(12分)用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,试问:不同的染色方法的种数是多少?
七. 递推法
1.一个楼梯共18个台阶12步登完,可一步登一个台阶也可一步登两个台阶,一共有多少种不同的走法.
解 根据题意要想12步登完只能6个一步登一个台阶,6个一步登两个台阶,因此,把问题转化为6个相同的黑球与6个相同的白球的排列问题.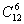 =924(种).
=924(种).
例八 一楼梯共10级,如果规定每次只能跨上一级或两级,要走上这10级楼梯,共有多少种不同的走法?
分析:设上n级楼梯的走法为an种,易知a1=1,a2=2,当n≥2时,上n级楼梯的走法可分两类:第一类:是最后一步跨一级,有an-1种走法,第二类是最后一步跨两级,有an-2种走法,由加法原理知:an=an-1+ an-2,据此,a3=a1+a2=3,a4=a#+a2=5,a5=a4+a3=8,a6=13,a7=21,a8=34,a9=55,a10=89.故走上10级楼梯共有89种不同的方法。
例2:五个人排成一列,重新站队时,各人都不站在原来的位置上,那么不同的站队方式共有( )
(A)60种 (B)44种 (C)36种 (D)24种
解:首先我们把人数推广到 个人,即
个人,即 个人排成一列,重新站队时,各人都不站在原来的位置上。设满足这样的站队方式有
个人排成一列,重新站队时,各人都不站在原来的位置上。设满足这样的站队方式有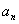 种,现在我们来通过合理分步,恰当分类找出递推关系:
种,现在我们来通过合理分步,恰当分类找出递推关系:
第一步:第一个人不站在原来的第一个位置,有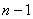 种站法。
种站法。
第二步:假设第一个人站在第2个位置,则第二个人的站法又可以分为两类:第一类,第二个人恰好站在第一个位置,则余下的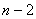 个人有
个人有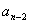 种站队方式;第二类,第二个人不站在第一个位置,则就是第二个人不站在第一个位置,第三个人不站在第三个位置,第四个人不站在第四个位置,……,第
种站队方式;第二类,第二个人不站在第一个位置,则就是第二个人不站在第一个位置,第三个人不站在第三个位置,第四个人不站在第四个位置,……,第 个人不站在第
个人不站在第 个位置,所以有
个位置,所以有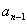 种站队方式。
种站队方式。
由分步计数原理和分类计数原理,我们便得到了数列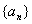 的递推关系式:
的递推关系式:
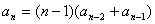 ,显然,
,显然,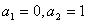 ,再由递推关系有
,再由递推关系有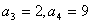 ,
,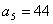 ,故应选(B)
,故应选(B)
九.几何问题
1.四面体的一个顶点位A,从其它顶点与各棱中点取3个点,使它们和点A在同一平面上,不同的取法有 种(3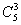 +3=33)
+3=33)
2.四面体的棱中点和顶点共10个点(1)从中任取3个点确定一个平面,共能确定多少个平面?
(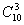 -4
-4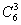 +4-3
+4-3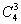 +3-6C
+3-6C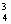 +6+2×6=29)
+6+2×6=29)
(2)以这10个点为顶点,共能确定多少格凸棱锥? 三棱锥 C104-4C64-6C44-3C44=141 四棱锥 6×4×4=96 3×6=18 共有114
例15.正方体8个顶点中取出4个,可组成多少个四面体? 【 ∴ 共-12=70-12=58个】
(2)可以组成多少个四棱锥?(48个)
十.先选后排法
例9 有甲乙丙三项任务,甲需2人承担,乙丙各需1人承担,从10人中选派4人承担这三项任务,不同的选派方法有( )
A.1260种 B.2025种 C.2520种 D.5054种
分析:先从10人中选出2人
33、(浙江省09年高考省教研室第一次抽样测试数学试题(理))现安排5人去三个地区做志愿者,每个地区至少去1人,其中甲、乙不能去同一个地区,那么这样的安排方法共有 种【答案:114
9、(陕西省西安铁一中20##届高三12月月考)某校高三级有三位数学老师,为便于学生询问,从星期一到星期五每天都安排数学教师值班,并且星期一安排两位老师值班,若每位老师每周值班两天,则一周内安排值班的方案有 种. 答案:36
例8. 将4名教师分派到3所中学任教,每所中学至少1名教师,则不同的分派方案共有多少种?
答案:36
1.安排三名老师去6所学校任教,每校至多2人,则不同的分配方案共有(210)种。
2.将5名实习教师分配到高一年级的3个班实习,每班至少1人,至多2人,则不同的分配方案(90种)。
9.(湖北卷6)将5名志愿者分配到3个不同的奥运场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为D A. 540 B. 300 C. 180 D. 150
3.将9个学生分配到甲乙丙三个宿舍,每个宿舍至多4人(床铺不分次序),则不同的分配方案(1130种)。
例6.在11名工人中,有5人只能当钳工,4人只能当车工,另外2人能当钳工也能当车工。现从11人中选出4人当钳工,4人当车工,问共有多少种不同的选法? 185
6.甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一、乙不值周六,则可排出不同的值班表数为 。42
8.已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,则符合这些条件的直线有 43 条。
十一.用转换法解排列组合问题(包括构造插空,捆绑;构造隔板;)
例10.某人连续射击8次有四次命中,其中有三次连续命中,按“中”与“不中”报告结果,不同的结果有多少种.
解 把问题转化为四个相同的黑球与四个相同白球,其中只有三个黑球相邻的排列问题.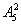 =20种
=20种
例13. 马路上有编号为l,2,3,……,10 十个路灯,为节约用电又看清路面,可以把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,在两端的灯也不能关掉的情况下,求满足条件的关灯方法共有多少种? 20种
例12 从1,2,3,…,1000个自然数中任取10个不连续的自然数,有多少种不同的去法.
解 把稳体转化为10个相同的黑球与990个相同白球,其其中黑球不相邻的排列问题。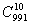
1.有3个相同的白球,4个相同的黑球,则能组成多少种不同的排法?(35)
2.今有2个红球,3个黄球,4个白球,同色球不加区分,将9个球排成一列有(1260)种
4. 某城市街道呈棋盘形,南北向大街5条,东西向大街4条,一人欲从西南角走到东北角,路程最短的走法有多少种.
解 无论怎样走必须经过三横四纵,因此,把问题转化为3个相同的白球与四个相同的黑球的排列问题.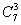 =35(种)
=35(种)
1. 一个楼梯共18个台阶12步登完,可一步登一个台阶也可一步登两个台阶,一共有多少种不同的走法.
解 根据题意要想12步登完只能6个一步登一个台阶,6个一步登两个台阶,因此,把问题转化为6个相同的黑球与6个相同的白球的排列问题.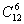 =924(种).
=924(种).
2.(理)甲、乙、丙三人传球,第一次球从甲手中传出,到第六次球又回到甲手中的传递
方式有_____22____种
例7:甲、乙、丙、丁四人相互传球,第一次甲传给乙、丙、丁中的任一人,第二次由拿球者再传给其他人中任一人,这样共传了四次,则第四次球仍传回到甲的方法共有( A )
(A)21种 (B)42 (C)24 (D)27
3.6个人参加秋游带10瓶饮料,每人至少带1瓶,一共有多少钟不同的带法.
解 把问题转化为5个相同的白球不相邻地插入已经排好的10个相同的黑球之间的9个空隙种的排列问题. =126种
=126种
例13 求(a+b+c)10的展开式的项数.
解 展开使的项为aαbβcγ,且α+β+γ=10,因此,把问题转化为2个相同的黑球与10个相同的白球的排列问题.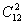 =66(种)
=66(种)
例14 亚、欧乒乓球对抗赛,各队均有5名队员,按事先排好的顺序参加擂台赛,双方先由1号队员比赛,负者淘汰,胜者再与负方2号队员比赛,直到一方全被淘汰为止,另一方获胜,形成一种比赛过程.那么所有可能出现的比赛过程有多少种?
解 设亚洲队队员为a1,a2,…,a5,欧洲队队员为b1,b2,…,b5,下标表示事先排列的出场顺序,若以依次被淘汰的队员为顺序.比赛过程转化为这10个字母互相穿插的一个排列,最后师胜队种步被淘汰的队员和可能未参加参赛的队员,所以比赛过程可表示为5个相同的白球和5个相同黑球排列问题,比赛过程的总数为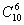 =252(种)
=252(种)
十二.转化命题法
例15 圆周上共有15个不同的点,过其中任意两点连一弦,这些弦在圆内的交点最多有多少各?
分析:因两弦在圆内若有一交点,则该交点对应于一个以两弦的四端点为顶点的圆内接四边形,则问题化为圆周上的15个不同的点能构成多少个圆内接四边形,因此这些现在圆内的交点最多有 =1365(个)
=1365(个)
例16 圆周上共有n(n大于等于4)个不同的点,过其中任意两点连一弦,这些弦在圆内的交点最多有多少各?
十三.概率法
例17 一天的课程表要排入语文、数学、物理、化学、英语、体育六节课,如果数学必须排在体育之前,那么该天的课程表有多少种排法?
分析:在六节课的排列总数中,体育课排在数学之前与数学课排在体育之前的概率相等,均为 ,故本例所求的排法种数就是所有排法的
,故本例所求的排法种数就是所有排法的 ,即
,即 A=360种
A=360种
十四.除序法
例:7个节目,甲、乙、丙三个节目按给定顺序出现,有多少种排法?
分析:7个节目的全排列为A77,甲、乙、丙之间的顺序已定。所以有A77∕A33=840种。
答案:840种。
例19 用1,2,3,4,5,6,7这七个数字组成没有重复数字的七位数中,
(1)若偶数2,4,6次序一定,有多少个?
(2)若偶数2,4,6次序一定,奇数1,3,5,7的次序也一定的有多少个?
解(1)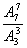 (2)
(2)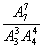
十五.错位排列
例20 同室四人各写一张贺卡,先集中起来,然后每人从中拿一张别人送出的卡片,则不同的分配方法有 种(9)
公式 1)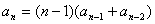 n=4时a4=3(a3+a2)=9种 即三个人有两种错排,两个人有一种错排.
n=4时a4=3(a3+a2)=9种 即三个人有两种错排,两个人有一种错排.
2)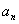 =n!(1-
=n!(1-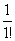 +
+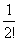 -
-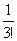 +…+
+…+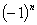
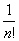
例2:五个人排成一列,重新站队时,各人都不站在原来的位置上,那么不同的站队方式共有( )
(A)60种 (B)44种 (C)36种 (D)24种
练习 有五位客人参加宴会,他们把帽子放在衣帽寄放室内,宴会结束后每人戴了一顶帽子回家,回家后,他们的妻子都发现他们戴了别人的帽子,问5位客人都不戴自己帽子的戴法有多少种?(44)
十六。圆桌问题
20.8个人做圆桌共有多少组合?
21.5个男孩,三个女孩围成一圈,其中三个女孩不相邻,则有多少种站法?
21、(重庆市万州区20##级高三第一次诊断性试题)一圆形餐桌依次有A、B、C、D、E、F共6个座位.现让3个大人和3个小孩入座进餐,要求任何两个小孩都不能坐在一起,则不同的入座方法总数为( )
(A)24种 (B)48种 (C)72种 (D)144种
答案:C
