数值方法实验报告
课程名称:LU分解法与高斯消元法
学 院:数学与财经学院
专 业:信息与计算科学(金融软件)
年 级:2011级
姓 名:郑 荐
学 号:201102334023
指导教师:李 梦
实验一
【实验名称】
实现LU算法,并利用该算法求解线性方程组
【实验目的】
了解如何用LU三角分解法解线性方程组,利用LU三角分解法解线性方程组
【实验原理】
设无行交换变换的高斯消去法可求解一般线性方程组AX=B,则矩阵A可分解为一个下三角矩阵L和一个上三角矩阵U乘积:
A=LU
而且L的对角线元素为1,U的对角线元素非零。得到L和U后,可通过如下步骤得到X:
1. 利用向前替换法对方程组LY=B求解Y。
2. 利用回带法对方程组UX=Y求解X。
【实验步骤】
1. 输入矩阵A
2. LU分解A,得到L矩阵与U矩阵的值 [L U]=LU_1(A)
3. 输入矩阵B,利用向前回带法求出Y值 Y=upsub(L,B)
4. 利用回带发求出X值 [X]=backsub(U,Y)
【实验程序】
1. LU分解
代码:
function [L U]=LU_1(A)
n=length(A(1,:));
L=eye(n);
U=zeros(n);
for j=1:n
U(1,j)=A(1,j);
end
for i=2:n
L(i,1)=A(i,1)/U(1,1);
end
for k=2:n
for j=k:n
U(k,j)=A(k,j)-L(k,1:k-1)*U(1:k-1,j);
end
for i=k+1:n
L(i,k)=(A(i,k)-L(i,1:k-1)*U(1:k-1,k))/U(k,k);
end
end
结果:
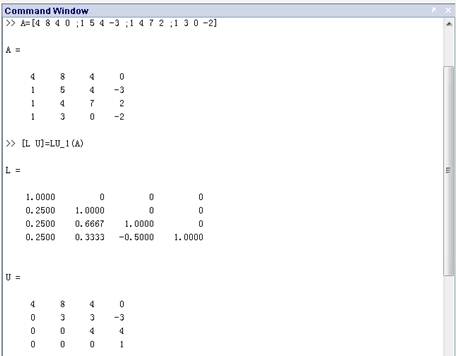
2. 向前回带法
代码:
%向前代入法
function Y=upsub(A,B)
n=length(B);
Y=zeros(n,1);
Y(1)=B(1)/A(1,1);
for k=2:n
Y(k)=(B(k)-A(k,1:k-1)*Y(1:k-1))/A(k,k);
end
结果:

3. 回带法
代码:
%回代法
function [X]=backsub(A,B)
n=length(B);
X=zeros(n,1);
X(n)=B(n)/A(n,n);
for k=n-1:(-1):1
X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k);
end
结果:

【实验分析】
LU分解法比较简便迅速,当解多个系数矩阵为A的线性方程做时,LU分解法就显得特别优越,只要对系数矩阵做一次LU分解,以后只要解三角形方程即可。也可以根据系数矩阵的形状来设计算法。
实验二
【实验名称】
高斯消元法解线性方程组
【实验目的】
了解如何用高斯消元法解线性方程组,利用高斯消元法解线性方程组
【实验原理】
消元过程:
设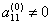 ,令乘数
,令乘数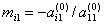 ,做(消去第i个方程组的
,做(消去第i个方程组的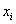 )操作
)操作 ×第1个方程+第i个方程(i=2,3,.....n)
×第1个方程+第i个方程(i=2,3,.....n)
则第i个方程变为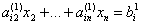
这样消去第2,3,。。。,n个方程的变元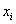 后。原线性方程组变为:
后。原线性方程组变为:
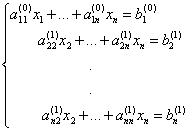
这样就完成了第1步消元。
回代过程:
在最后的一方程中解出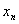 ,得:
,得: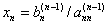
再将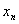 的值代入倒数第二个方程,解出
的值代入倒数第二个方程,解出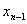 ,依次往上反推,即可求出方程组的解:
,依次往上反推,即可求出方程组的解:
其通项为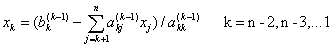
【实验步骤】
1、输入A和b
2、判断是否有解
B=[A b]
if RA<RB,无解
return,end
else RA=RB 转3
3、if RA=RB=n 有唯一解
对 k=1:n-1 做A(k,k)=0,break
for i=k+1:n
L(i,k)=A(i,k)/A(k,k)
A(i,k)=A(i,j)-L(i,k)*A(i,j)
end
end
4、 elseif RA=RB<n时,有无穷解,end
5、 后向代入法求解
【实验程序】
回带法程序:
%回代法
function [X]=backsub(A,B)
n=length(B);
X=zeros(n,1);
X(n)=B(n)/A(n,n);
for k=n-1:(-1):1
X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k);
end
高斯消元法程序:
function[RA,RB,n]=gaus(A,b)
B=[A b];
n=length(b);
RA=rank(A);
RB=rank(B);
rank_dif=RB-RA;
if rank_dif>0
disp('RA~RB,此方程无解');
return;
end
if RA==RB
if RA==n
disp('RA=RB=n,次方程组有唯一解');
X=zeros(n,1);
for p=1:n-1
for k=p+1:n
m=B(k,p)/B(p,p);
B(k,p:n+1)=B(k,p:n+1)-m*B(p,p:n+1);
end
end
X=backsub(B(1:n,1:n),B(1:n,n+1));
X
else
disp('RA=RB<n,次方程组有无穷解。')
end
end
结果:
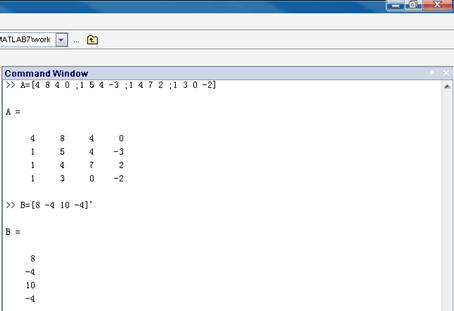
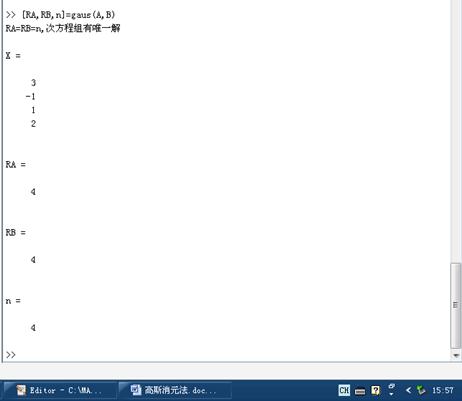
【实验分析】
高斯消元法代码更为复杂。LU分解的方法,求解方程组的方法使得得出的结果更加精确。高斯消元法能更快判断出是由有解。LU分解法在LU分解前矩阵A不知道能否可以分解。
【实验心得】
本次试验涉及到了用高斯消元法,LU分解法两种方法。需要对这些方法的原理都要掌握才能写出程序,由于理论知识的欠缺,我花了很大一部分时间在看懂实验的原理上,看懂了实验原理之后就开始根据原理编写程序,程序中还是出现了很多的低级错误导致调试很久才能运行。通过这次试验使我深刻的体会到理论知识的重要性,没有理论知识的支撑是写不出程序来的。写程序时还会犯很多低级的错误,以后一定要加强理论知识的学习,减少编程时低级错误的产生。
第二篇:高斯消元法(完整)
高斯消元法解线性方程组
在工程技术和工程管理中有许多问题经常可以归结为线性方程组类型的数学模型,这些模型中方程和未知量个数常常有多个,而且方程个数与未知量个数也不一定相同。那么这样的线性方程组是否有解呢?如果有解,解是否唯一?若解不唯一,解的结构如何呢?这就是下面要讨论的问题。
一、线性方程组
设含有n个未知量、有m个方程式组成的方程组
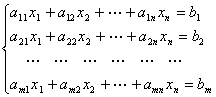 (3.1)
(3.1)
其中系数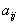 ,常数
,常数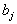 都是已知数,
都是已知数,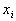 是未知量(也称为未知数)。当右端常数项
是未知量(也称为未知数)。当右端常数项 ,
, 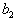 , …,
, …,  不全为0时,称方程组(3.1)为非齐次线性方程组;当
不全为0时,称方程组(3.1)为非齐次线性方程组;当 =
=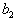 = … =
= … = = 0时,即
= 0时,即
 (3.2)
(3.2)
称为齐次线性方程组。
由n个数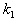 ,
, 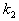 , …,
, …, 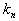 组成的一个有序数组(
组成的一个有序数组(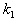 ,
, 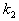 , …,
, …, 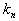 ),如果将它们依次代入方程组(3.1)中的
),如果将它们依次代入方程组(3.1)中的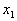 ,
, 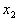 , …,
, …, 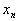 后,(3.1)中的每个方程都变成恒等式,则称这个有序数组(
后,(3.1)中的每个方程都变成恒等式,则称这个有序数组(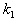 ,
, 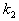 , …,
, …, 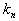 )为方程组(3.1)的一个解。显然由
)为方程组(3.1)的一个解。显然由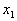 =0,
=0, 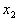 =0, …,
=0, …, 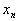 =0组成的有序数组(0, 0, …, 0)是齐次线性方程组(3.2)的一个解,称之为齐次线性方程组(3.2)的零解,而当齐次线性方程组的未知量取值不全为零时,称之为非零解。
=0组成的有序数组(0, 0, …, 0)是齐次线性方程组(3.2)的一个解,称之为齐次线性方程组(3.2)的零解,而当齐次线性方程组的未知量取值不全为零时,称之为非零解。
(利用矩阵来讨论线性方程组的解的情况或求线性方程组的解是很方便的。因此,我们先给出线性方程组的矩阵表示形式。)
非齐次线性方程组(3.1)的矩阵表示形式为:
AX = B
其中
A =  ,X =
,X = 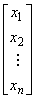 ,B =
,B = 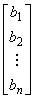
称A为方程组(3.1)的系数矩阵,X为未知矩阵,B为常数矩阵。将系数矩阵A和常数矩阵B放在一起构成的矩阵
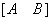 =
=
称为方程组(3.1)的增广矩阵。
齐次线性方程组(3.2)的矩阵表示形式为:AX = O
二、高斯消元法
(下面介绍利用矩阵求解方程组的方法,那么矩阵初等行变换会不会改变方程组的解呢?我们先看一个定理。)
定理3.1 若用初等行变换将增广矩阵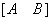 化为
化为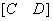 ,则AX = B与CX = D是同解方程组。
,则AX = B与CX = D是同解方程组。
证 由定理3.1可知,存在初等矩阵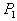 ,
, 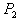 , …,
, …, 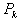 ,使
,使
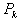 …
…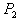
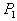
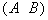 =
= 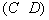
记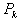 …
…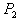
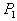 = P,则P可逆,即
= P,则P可逆,即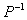 存在。
存在。
设 为方程组A X = B的解,即
为方程组A X = B的解,即
A = B
= B
在上式两边左乘P,得
P A = PB
= PB
即
C = D
= D
说明 也是方程组C X = D的解。反之,设
也是方程组C X = D的解。反之,设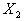 为方程组C X = D的解,即
为方程组C X = D的解,即
C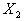 = D
= D
在上式两边左乘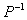 ,得
,得
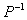 C
C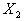 =
= 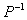 D
D
即
A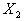 = B
= B
说明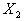 也是方程组AX = B的解。
也是方程组AX = B的解。
因此,方程组A X = B与C X = D的解相同,即它们是同解方程组。(证毕)
(由定理3.1可知,求方程组(3.1)的解,可以利用初等行变换将其增广矩阵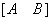 化简。又有第二章定理2.10可知,通过初等行变换可以将
化简。又有第二章定理2.10可知,通过初等行变换可以将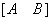 化成阶梯形矩阵。因此,我们得到了求解线性方程组(3.1)的一般方法:)
化成阶梯形矩阵。因此,我们得到了求解线性方程组(3.1)的一般方法:)
用初等行变换将方程组(3.1)的增广矩阵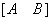 化成阶梯形矩阵,再写出该阶梯形矩阵所对应的方程组,逐步回代,求出方程组的解。因为它们为同解方程组,所以也就得到了原方程组(3.1)的解。这种方法被称为高斯消元法,
化成阶梯形矩阵,再写出该阶梯形矩阵所对应的方程组,逐步回代,求出方程组的解。因为它们为同解方程组,所以也就得到了原方程组(3.1)的解。这种方法被称为高斯消元法,
(下面举例说明用消元法求一般线性方程组解的方法和步骤。)
例1 解线性方程组  (3.3)
(3.3)
解 先写出增广矩阵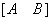 ,再用初等行变换将其逐步化成阶梯形矩阵,即
,再用初等行变换将其逐步化成阶梯形矩阵,即
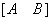 =
=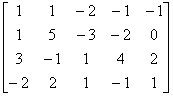
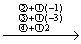
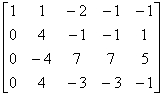
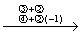
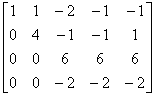
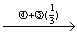

上述四个增广矩阵所表示的四个线性方程组是同解方程组,最后一个增广矩阵表示的线性方程组为
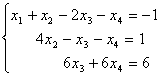
将最后一个方程乘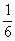 ,再将
,再将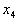 项移至等号的右端,得
项移至等号的右端,得
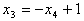
将其代入第二个方程,解得
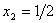
再将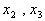 代入第一个方程组,解得
代入第一个方程组,解得
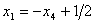
因此,方程组(3.3)的解为
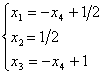 (3.4)
(3.4)
其中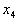 可以任意取值。
可以任意取值。
由于未知量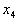 的取值是任意实数,故方程组(3.3)的解有无穷多个。由此可知,表示式(3.4)表示了方程组(3.3)的所有解。表示式(3.4)中等号右端的未知量
的取值是任意实数,故方程组(3.3)的解有无穷多个。由此可知,表示式(3.4)表示了方程组(3.3)的所有解。表示式(3.4)中等号右端的未知量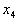 称为自由未知量,用自由未知量表示其它未知量的表示式(3.4)称为方程组(3.3)的一般解,当表示式(3.4)中的未知量
称为自由未知量,用自由未知量表示其它未知量的表示式(3.4)称为方程组(3.3)的一般解,当表示式(3.4)中的未知量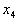 取定一个值(如
取定一个值(如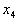 =1),得到方程组(3.3)的一个解(如
=1),得到方程组(3.3)的一个解(如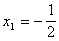 ,
,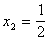 ,
,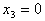 ,
,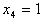 ),称之为方程组(3.3)的特解。
),称之为方程组(3.3)的特解。
注意,自由未知量的选取不是唯一的,如例1也可以将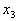 取作自由未知量。
取作自由未知量。
如果将表示式(3.4)中的自由未知量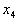 取一任意常数k,即令
取一任意常数k,即令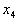 = k,那么方程组(3.3)的一般解为
= k,那么方程组(3.3)的一般解为
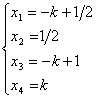 ,其中k为任意常数。
,其中k为任意常数。
用矩阵形式表示为
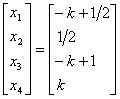 =
=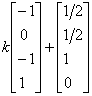 (3.5)
(3.5)
其中k为任意常数。称表示式(3.5)为方程组(3.3)的全部解。
(用消元法解线性方程组的过程中,当增广矩阵经过初等行变换化成阶梯形矩阵后,要写出相应的方程组,然后再用回代的方法求出解。如果用矩阵将回代的过程表示出来,我们可以发现,这个过程实际上就是对阶梯形矩阵进一步简化,使其最终化成一个特殊的矩阵,从这个特殊矩阵中,就可以直接解出或“读出”方程组的解。例如,)对例1中的阶梯形矩阵进一步化简,



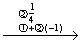

上述矩阵对应的方程组为
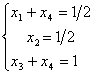
将此方程组中含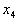 的项移到等号的右端,就得到原方程组(3.3)的一般解,
的项移到等号的右端,就得到原方程组(3.3)的一般解,
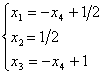 (3.4)
(3.4)
其中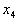 可以任意取值。
可以任意取值。
例2 解线性方程组 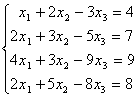
解 利用初等行变换,将方程组的增广矩阵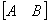 化成阶梯阵,再求解。即
化成阶梯阵,再求解。即
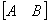 =
=

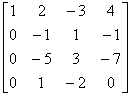





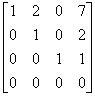

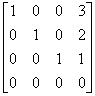
一般解为
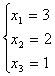
例3 解线性方程组 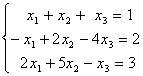
解 利用初等行变换,将方程组的增广矩阵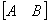 化成阶梯阵,再求解。即
化成阶梯阵,再求解。即
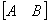 =
=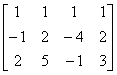

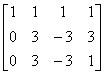


阶梯形矩阵的第三行“0, 0, 0, -2”所表示的方程为: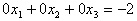 ,由该方程可知,无论
,由该方程可知,无论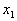 ,
,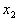 ,
,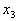 取何值,都不能满足这个方程。因此,原方程组无解。
取何值,都不能满足这个方程。因此,原方程组无解。
三、线性方程组的解的判定
前面介绍了用高斯消元法解线性方程组的方法,通过例题可知,线性方程组的解的情况有三种:无穷多解、唯一解和无解。从求解过程可以看出,方程组(3.1)是否有解,关键在于增广矩阵[A B]化成阶梯非零行的行数与系数矩阵A化成阶梯形矩阵后非零行的行数是否相等。因此,线性方程组是否有解,就可以用其系数矩阵和增广矩阵的秩来描述了。
定理3.9 线性方程组(3.1)有解的充分必要是 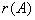 =
=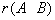 。
。
证 设系数矩阵A的秩为r,即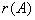 = r。利用初等行变换将增广矩阵[A B]化成阶梯阵:
= r。利用初等行变换将增广矩阵[A B]化成阶梯阵:
[A B]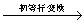
 = [C D]
= [C D]
故AX = B与CX = D是同解方程组,因此
AX = B有解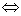
 = 0
= 0 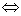
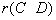 =
=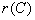 = r
= r
即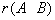 =
=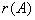 = r。 (证毕)
= r。 (证毕)
推论1 线性方程组有唯一解的充分必要条件是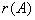 =
=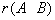 =
= 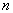 。
。
推论2 线性方程组有无穷多解的充分必要条件是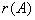 =
=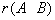

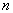 。
。
(将上述结论应用到齐次线性方程组(3.2)上,则总有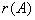 =
=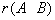 。因此齐次线性方程组一定有解。并且有)
。因此齐次线性方程组一定有解。并且有)
例4 判别下列方程组是否有解?若有解,是有唯一解还是有无穷多解?
(1) 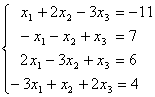 (2)
(2) 
(3) 
解 (1) 用初等行变换将增广矩阵化成阶梯阵,即
[A B ]=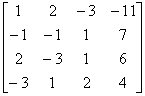

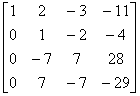

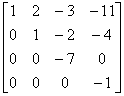
因为 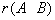 = 4,
= 4,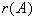 =3,两者不等,所以方程组无解。
=3,两者不等,所以方程组无解。
(2) 用初等行变换将增广矩阵化成阶梯阵,即
[A B ]=
 …
… 
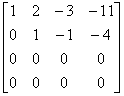
因为 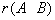 =
=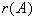 =2
=2 n(= 3),所以方程组有无穷多解。
n(= 3),所以方程组有无穷多解。
(3) 用初等行变换将增广矩阵化成阶梯形矩阵,即
[A B ]=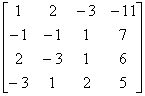
 …
… 
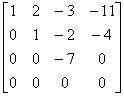
因为 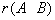 =
=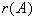 = 3 = n,所以方程组有唯一解。
= 3 = n,所以方程组有唯一解。
例5 判别下列齐次方程组是否有非零解? (机动)
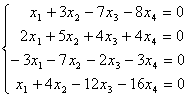
解 用初等行变换将系数矩阵化成阶梯形矩阵,即
A =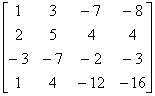

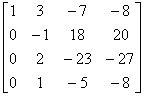




因为 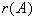 = 4 = n,所以齐次方程组只有零解。
= 4 = n,所以齐次方程组只有零解。
向量组的相关性
在实际问题有许多研究的对象要用n元有序数组来表示。如总结某五年计划各年某产品产量的数据资料,某工程一年12个月份的用料情况等,就分别要用到5元和12元有序数组。
一、n维向量的定义
定义3.2 把有顺序的n个数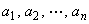 称为一个n维向量,记作
称为一个n维向量,记作

其中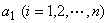 称为n维向量
称为n维向量 的第i个分量。
的第i个分量。
例如,矩阵 A =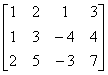 中每一列都可以看作三维向量:
中每一列都可以看作三维向量:
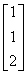 ,
, ,
, ,
,
称为矩阵A的列向量。A中的每一行都可以看作四维向量:
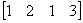 ,
,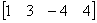 ,
,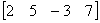
称为矩阵A的行向量。
规定:n维向量相等、相加、数乘与列矩阵对应相等。
二、n维向量组的线性相关性
如果把方程组
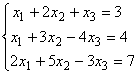 (3.6)
(3.6)
用向量相等、向量运算关系来表示:
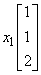 +
+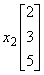 +
+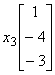 =
=
那么方程组求解问题就变成了求一组使上式列向量存在某种的数 了。下面给出向量之间这种关系的定义。
了。下面给出向量之间这种关系的定义。
定义3.3 对于向量 ,
,  ,如果有一组数
,如果有一组数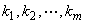 ,使得
,使得
 =
=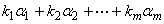
则称 是
是 的线性组合,或称
的线性组合,或称 由
由 线性表出,且称这组数
线性表出,且称这组数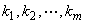 为组合系数。
为组合系数。
例1 二维向量组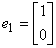 ,
, ,称为二维单位向量组。任意一个二维向量
,称为二维单位向量组。任意一个二维向量 都可以由
都可以由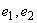 线性表出:
线性表出: 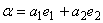 。
。
例2 向量 不是向量
不是向量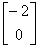 和
和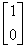 的线性组合,因为对于任意一组数
的线性组合,因为对于任意一组数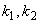 ,
,
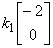 +
+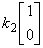 =
=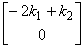

例3 向量组 中的任一向量
中的任一向量 都能由这个向量组线性表出:
都能由这个向量组线性表出:
 =
=
如果用列向量分别把方程组(3.6)的系数矩阵第j列和常数列表示为
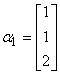 ,
, ,
, ,
,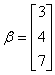
那么方程组(3.6)可以用向量形式表示为
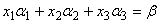
若方程组(3.6)有解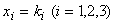 ,则有
,则有
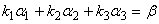
即向量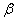 可以由向量组
可以由向量组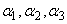 线性表出。反之,若存在数
线性表出。反之,若存在数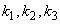 使得上式成立,则
使得上式成立,则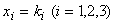 就是方程组(3.6)的一组解。
就是方程组(3.6)的一组解。
命题1 向量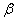 可以由向量组
可以由向量组 线性表出的充分必要条件是:以
线性表出的充分必要条件是:以 为系数列向量,以
为系数列向量,以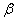 为常数列向量的线性方程组有解,并且此线性方程组的一组解就是线性组合的一组系数。
为常数列向量的线性方程组有解,并且此线性方程组的一组解就是线性组合的一组系数。
例4 设  ,
,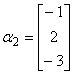 ,
, ,
,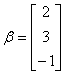
判断向量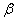 能否由向量组
能否由向量组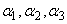 线性表出,若能够,写出它的一种表达式。
线性表出,若能够,写出它的一种表达式。
解 设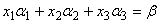 ,由此可得
,由此可得
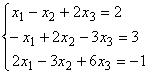
因为
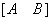 =
=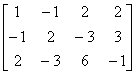
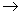
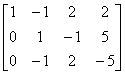
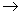

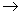

方程组的解为 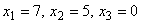 。 所以
。 所以 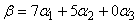 。
。
定义3.3 对于向量组 ,若存在m个不全为零的数
,若存在m个不全为零的数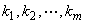 ,使得
,使得
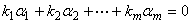 (3.7)
(3.7)
则称向量组 线性相关;否则称向量组
线性相关;否则称向量组 线性无关。
线性无关。
例5 式证单位向量组
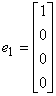 ,
,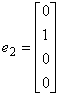 ,
,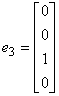 ,
,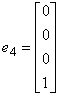
是线性无关的。
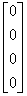
证 设 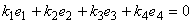 。即
。即
 +
+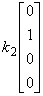 +
+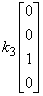 +
+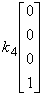 =
=
由上式得唯一解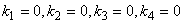 。所以,
。所以,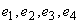 线性无关。
线性无关。
可以证明,n维单位向量组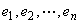 是线性无关的。
是线性无关的。
n维单位向量组 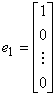 ,
,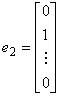 ,… ,
,… ,
如果把定义3.3中的(3.7)式看作以 为系数列向量,以
为系数列向量,以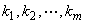 为未知量的齐次线性方程组,那么
为未知量的齐次线性方程组,那么
定理3.2 对于向量组 ,若齐次线性方程组
,若齐次线性方程组
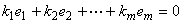 (3.8)
(3.8)
有非零解,则向量组 线性相关;若齐次线性方程组(3.8)只有零解,则向量组
线性相关;若齐次线性方程组(3.8)只有零解,则向量组 线性无关。
线性无关。
定理3.3 关于向量组 ,设矩阵
,设矩阵
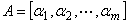
若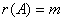 ,则向量组
,则向量组 线性无关;若
线性无关;若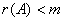 ,则向量组
,则向量组 线性相关。
线性相关。
推论 任意n+1个n维向量一定线性相关。
例6 判断下列向量组的相关性:
(1) 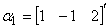 ,
, ,
,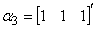 ;
;
(2) 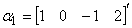 ,
,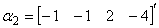 ,
,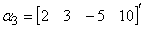 ;
;
(3)  ,
,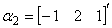 ,
,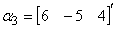 ,
,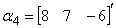 。
。
解 (1) 因为
A =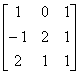

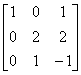


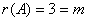 ,所以向量组
,所以向量组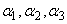 线性无关。
线性无关。
(2) 因为
B = 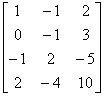

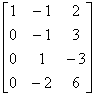

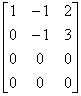
 ,所以向量组
,所以向量组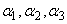 线性相关。
线性相关。
(3) 由推论知道,四个三维向量一定是线性相关的。
上面介绍了利用定理3.3来判断向量组的相关性,下面再介绍一个揭示同组向量之间具有某种相关性的特点。
定理3.4 向量组 ,
,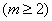 线性相关的充分必要条件是:其中至少有一个向量可以由其余向量线性表出。
线性相关的充分必要条件是:其中至少有一个向量可以由其余向量线性表出。
(证明请参阅教材)
推论 向量组 ,
,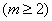 线性无关的充分必要条件是:其中每一个向量都不能由其余向量线性表出。
线性无关的充分必要条件是:其中每一个向量都不能由其余向量线性表出。
例7 试证:若向量组的一个部分向量组线性相关,则整个向量组也线性相关。
证 不妨设向量组 中的部分向量组
中的部分向量组
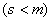 线性相关,则存在不全为零的数
线性相关,则存在不全为零的数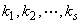 ,使得
,使得
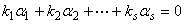
从而有
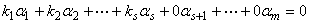
其中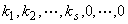 不全为零,所以向量组
不全为零,所以向量组 线性相关。
线性相关。
可以证明:若一个向量组线性无关,它的任意一个部分向量组也线性无关
例8 设向量组 线性无关,而向量组
线性无关,而向量组 ,
,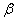 线性相关,证明
线性相关,证明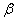 一定可以由
一定可以由 线性表出。
线性表出。
证 因为向量组 ,
,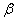 线性相关,即存在不全为零的数
线性相关,即存在不全为零的数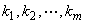 和
和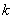 ,使得
,使得
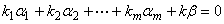
若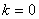 ,则上式为
,则上式为 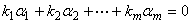 ,且
,且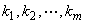 不全为零,得
不全为零,得 线性相关,与条件矛盾。因此
线性相关,与条件矛盾。因此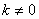 ,且
,且
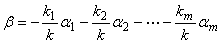
即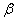 可以由
可以由 线性表出。
线性表出。
三、向量组的秩
(下面简单地介绍向量组的秩的概念及计算方法,首先向量组的极大无关组的定义)
定义3.4 若向量组S中的部分向量组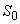 满足:
满足:
(1) 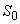 线性无关;
线性无关;
(2) S中的每一个向量都是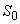 中向量的线性组合,则称部分向量组
中向量的线性组合,则称部分向量组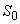 为向量组S的极大无关组。
为向量组S的极大无关组。
可以证明:对于一个向量组,其所有极大无关组所含向量个数都相同。因此向量组的秩定义如下:
定义3.5 对于向量组S,其极大无关组所含向量个数称为向量组S的秩。
利用定义求向量组的秩是比较困难的。但是,我们可以利用矩阵与列向量组之间的关系,把求向量组的秩的问题转化为求矩阵的秩序。这是因为
定理3.7 矩阵A的秩=矩阵A列向量组的秩=矩阵A行向量组的秩。
例9 设向量组
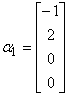 ,
,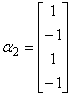 ,
,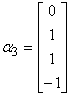 ,
,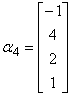
求向量组的秩及其一个极大无关组。
解 作矩阵A= ,用初等行变换求A的秩,即
,用初等行变换求A的秩,即
A= 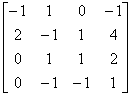


所以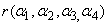 =3,且
=3,且 为其中的一个 极大无关组。
为其中的一个 极大无关组。
线性方程组解的结构
前两讲介绍了方程组的有关概念,方程组的解的几种情况及判定,向量组的相关性。这一讲主要介绍方程组解的结构。
一、齐次线性方程组解的结构
齐次线性方程组的矩阵形式为:AX = O
 (3.2)
(3.2)
解的情况可以归纳为:
1.齐次线性方程组只有零解的充分必要条件是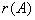 =
= 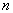 。
。
2.齐次线性方程组有非零解的充分必要条件是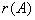

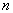 。
。
注意:当A为n阶方阵时也可利用矩阵行列式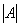 判断。
判断。
3.当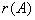 = r
= r
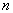 时,方程组AX = O有n-r个自由未知量。
时,方程组AX = O有n-r个自由未知量。
齐次线性方程组AX = O解的性质:
性质1 若 和
和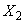 为齐次线性方程组AX = O的解,则
为齐次线性方程组AX = O的解,则 +
+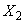 亦为AX = O的解。
亦为AX = O的解。
证 因为 和
和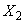 为方程组AX = O的两个解,故有
为方程组AX = O的两个解,故有
A = O, A
= O, A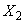 = O
= O
A( +
+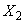 )= A
)= A + A
+ A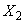 = O
= O
所以, +
+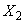 亦为AX = O的解。
亦为AX = O的解。
性质2 若 为齐次线性方程组AX = O的解,则k
为齐次线性方程组AX = O的解,则k 亦为AX = O的解,其中k为任意常数。
亦为AX = O的解,其中k为任意常数。
证 因为 为方程组AX = O的解,故有
为方程组AX = O的解,故有
A(k )= k(A
)= k(A )= O
)= O
所以,k 亦为AX = O的解。
亦为AX = O的解。
由性质1,2可知,若 ,
,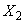 ,…,
,…,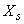 为方程组AX = O的解,则
为方程组AX = O的解,则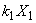 +
+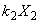 +…+
+…+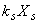 亦为AX = O的解,其中
亦为AX = O的解,其中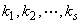 为任意常数。
为任意常数。
若 ,
,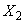 ,…,
,…,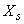 线性无关,且方程组AX = O的任何一个解X都可以被
线性无关,且方程组AX = O的任何一个解X都可以被 ,
,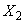 ,…,
,…,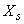 线性表出,则AX = O的全部解就是
线性表出,则AX = O的全部解就是
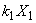 +
+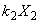 +…+
+…+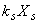
其中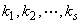 为任意常数。
为任意常数。
定义3.6 齐次线性方程组AX = O满足下列两个条件的一组解向量,称为AX = O的基础解系。
(1) 线性无关;
(2) 方程组AX = O的任何一个解都可以用它们线性表出。
(由定义3.6可知)方程组AX = O的基础解系就是其全部解向量的一个极大无关组。
当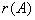 = n时,方程组AX = O只有零解,故不存在基础解系;而当
= n时,方程组AX = O只有零解,故不存在基础解系;而当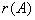 = r(<n)时,方程组AX = O有非零解,故存在基础解系,且基础解系中所含解向量的个数是n-r。由此可得如下结论:
= r(<n)时,方程组AX = O有非零解,故存在基础解系,且基础解系中所含解向量的个数是n-r。由此可得如下结论:
4.当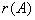 = r<n时,方程组AX = O一定有基础解系,且每个基础解系中含有n-r个解向量。若
= r<n时,方程组AX = O一定有基础解系,且每个基础解系中含有n-r个解向量。若 ,
,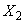 ,…,
,…,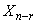 为基础解系,则AX = O的全部解为
为基础解系,则AX = O的全部解为
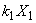 +
+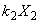 +…+
+…+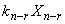 (3.9)
(3.9)
其中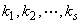 为任意常数。
为任意常数。
(3.9)式称为AX = O的通解。
如何求方程组AX = O的基础解系呢?
(1) 把齐次线性方程组的系数写成矩阵A;
(2) 用初等行变换把A化为阶梯阵;
(3) 把阶梯阵中非主元列所对应的变量作为自由未知量
(4) 分别令自由未知量中一个为1其余全部为0的办法,求出n-r个解向量,这n-r个解向量构成了基础解系。
例1 设齐次线性方程组
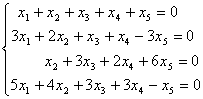
求其基础解系和通解。
解 先写出系数矩阵A,再用初等行变换将其逐步化成阶梯形矩阵,即
A =
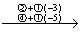
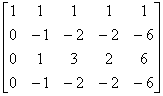
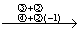
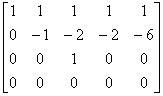
再进一步化简,得
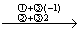



由此可知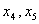 为自由未知量。
为自由未知量。
令 ,
,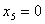 ,得解向量
,得解向量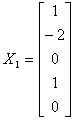 ;
;
令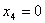 ,
,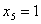 ,得解向量
,得解向量 ;
;
于是{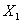 ,
,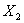 }为方程组的基础解系。通解为
}为方程组的基础解系。通解为
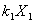 +
+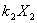
其中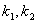 为任意常数。
为任意常数。
二、非齐次线性方程组解的结构
非齐次线性方程组的矩阵表示形式为:AX = B
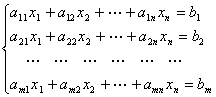
非齐次线性方程组AX = B的解的情况可以归纳为:
1.方程组AX = B有解的充分必要条件是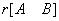 =
=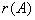 。
。
2.若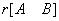 =
=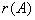 =
= 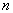 时,方程组AX = B有唯一解。
时,方程组AX = B有唯一解。
3.若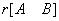 =
=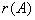 = r
= r
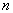 时,方程组AX = B有无穷多解,且有n-r个自由未知量。
时,方程组AX = B有无穷多解,且有n-r个自由未知量。
在非齐次线性方程组AX = B中,令B = O,得到相应的齐次方程组AX = O。
方程组AX = B与相应的AX = O之间有密切的关系,满足如下性质:
性质3 若 和
和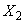 为非齐次线性方程组AX = B的解,则
为非齐次线性方程组AX = B的解,则 -
-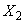 必为AX = O的解。
必为AX = O的解。
证 因为 和
和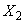 为方程组AX = B的两个解,故有
为方程组AX = B的两个解,故有
A = B, A
= B, A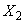 = B
= B
A( -
-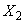 )= A
)= A - A
- A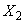 = B-B = O
= B-B = O
所以, -
-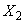 为AX = O的解。
为AX = O的解。
性质4 若 为非齐次线性方程组AX = B的解,
为非齐次线性方程组AX = B的解, 为相应的方程组AX = O的解,则
为相应的方程组AX = O的解,则 +
+ 必为AX = B的解。
必为AX = B的解。
证 因为 为方程组AX = B的解,
为方程组AX = B的解, 为方程组AX = O的解,故有
为方程组AX = O的解,故有
A = B, A
= B, A = O
= O
A( +
+ )= A
)= A +A
+A =B+O= B
=B+O= B
所以, +
+ 为AX = B的解。
为AX = B的解。
例1 解线性方程组  (3.3)
(3.3)
解 先写出增广矩阵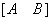 ,再用初等行变换将其逐步化成阶梯形矩阵,即
,再用初等行变换将其逐步化成阶梯形矩阵,即
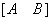 =
=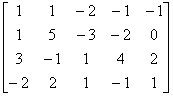
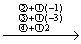
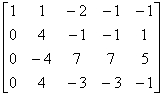
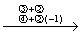

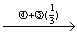

上述四个增广矩阵所表示的四个线性方程组是同解方程组,最后一个增广矩阵表示的线性方程组为
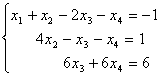
将最后一个方程乘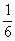 ,再将
,再将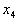 项移至等号的右端,得
项移至等号的右端,得
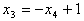
将其代入第二个方程,解得
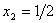
再将 代入第一个方程组,解得
代入第一个方程组,解得
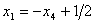
因此,方程组(3.3)的解为
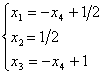 (3.4)
(3.4)
其中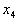 可以任意取值。
可以任意取值。
由于未知量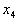 的取值是任意实数,故方程组(3.3)的解有无穷多个。由此可知,表示式(3.4)表示了方程组(3.3)的所有解。表示式(3.4)中等号右端的未知量
的取值是任意实数,故方程组(3.3)的解有无穷多个。由此可知,表示式(3.4)表示了方程组(3.3)的所有解。表示式(3.4)中等号右端的未知量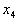 称为自由未知量,用自由未知量表示其它未知量的表示式(3.4)称为方程组(3.3)的一般解,当表示式(3.4)中的未知量
称为自由未知量,用自由未知量表示其它未知量的表示式(3.4)称为方程组(3.3)的一般解,当表示式(3.4)中的未知量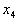 取定一个值(如
取定一个值(如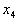 =1),得到方程组(3.3)的一个解(如
=1),得到方程组(3.3)的一个解(如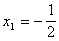 ,
,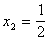 ,
,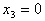 ,
,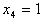 ),称之为方程组(3.3)的特解。
),称之为方程组(3.3)的特解。
注意,自由未知量的选取不是唯一的,如例1也可以将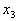 取作自由未知量。
取作自由未知量。
如果将表示式(3.4)中的自由未知量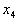 取一任意常数k,即令
取一任意常数k,即令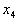 = k,那么方程组(3.3)的一般解为
= k,那么方程组(3.3)的一般解为
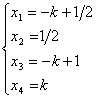 ,其中k为任意常数。
,其中k为任意常数。
用矩阵形式表示为
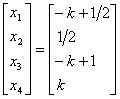 =
= (3.5)
(3.5)
其中k为任意常数。称表示式(3.5)为方程组(3.3)的全部解。
(用消元法解线性方程组的过程中,当增广矩阵经过初等行变换化成阶梯形矩阵后,要写出相应的方程组,然后再用回代的方法求出解。如果用矩阵将回代的过程表示出来,我们可以发现,这个过程实际上就是对阶梯形矩阵进一步简化,使其最终化成一个特殊的矩阵,从这个特殊矩阵中,就可以直接解出或“读出”方程组的解。例如,)对例1中的阶梯形矩阵进一步化简,



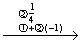

上述矩阵对应的方程组为
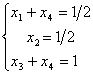
将此方程组中含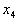 的项移到等号的右端,就得到原方程组(3.3)的一般解,
的项移到等号的右端,就得到原方程组(3.3)的一般解,
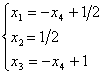 (3.4)
(3.4)
其中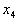 可以任意取值。
可以任意取值。
例2 解线性方程组 
解 利用初等行变换,将方程组的增广矩阵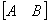 化成阶梯阵,再求解。即
化成阶梯阵,再求解。即
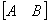 =
=

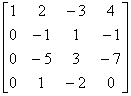








一般解为
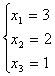
例3 解线性方程组 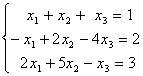
解 利用初等行变换,将方程组的增广矩阵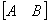 化成阶梯阵,再求解。即
化成阶梯阵,再求解。即
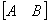 =
=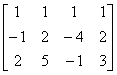

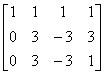


阶梯形矩阵的第三行“0, 0, 0, -2”所表示的方程为: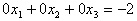 ,由该方程可知,无论
,由该方程可知,无论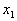 ,
,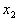 ,
,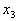 取何值,都不能满足这个方程。因此,原方程组无解。
取何值,都不能满足这个方程。因此,原方程组无解。
二、线性方程组的解的判定
前面介绍了用高斯消元法解线性方程组的方法,通过例题可知,线性方程组的解的情况有三种:无穷多解、唯一解和无解。从求解过程可以看出,方程组(3.1)是否有解,关键在于增广矩阵[A B]化成阶梯非零行的行数与系数矩阵A化成阶梯形矩阵后非零行的行数是否相等。因此,线性方程组是否有解,就可以用其系数矩阵和增广矩阵的秩来描述了。
定理3.9 线性方程组(3.1)有解的充分必要是 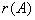 =
=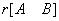 。
。
将上述结论应用到齐次线性方程组(3.2)上,则总有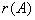 =
=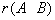 。因此齐次线性方程组一定有解。
。因此齐次线性方程组一定有解。
例4 判别下列方程组是否有解?若有解,是有唯一解还是有无穷多解?
(1) 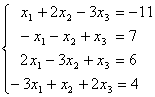 (2)
(2) 
(3) 
解 (1) 用初等行变换将增广矩阵化成阶梯阵,即
[A B ]=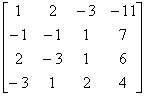
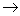
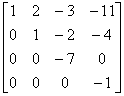
因为 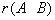 = 4,
= 4,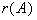 =3,两者不等,所以方程组无解。
=3,两者不等,所以方程组无解。
(2) 用初等行变换将增广矩阵化成阶梯阵,即
[A B ]=
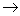 …
… 

因为 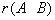 =
=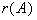 =2
=2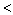 n(= 3),所以方程组有无穷多解。
n(= 3),所以方程组有无穷多解。
(3) 用初等行变换将增广矩阵化成阶梯形矩阵,即
[A B ]=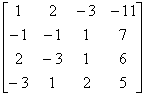
 …
… 
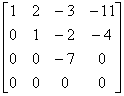
因为 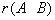 =
=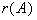 = 3 = n,所以方程组有唯一解。
= 3 = n,所以方程组有唯一解。
例5 判别下列齐次方程组是否有非零解?
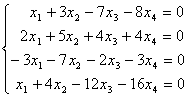
解 用初等行变换将系数矩阵化成阶梯形矩阵,即
A =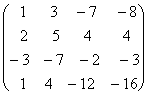
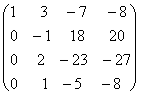


因为 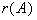 = 4 = n,所以齐次方程组只有零解。
= 4 = n,所以齐次方程组只有零解。
