重 庆 交 通 大 学
学 生 实 验 报 告
实验课程名称 数值计算方法II
开课实验室 数学实验室
学 院 理学院 年级 09 专业班
学 生 姓 名 学 号
开 课 时 间 2012 至 2013 学年第 2 学期

实验五 解线性方程组的直接方法
实验5.1 (主元的选取与算法的稳定性)
问题提出:Gauss消去法是我们在线性代数中已经熟悉的。但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss消去法作为数值算法的稳定性呢?Gauss消去法从理论算法到数值算法,其关键是主元的选择。主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。
实验内容:考虑线性方程组
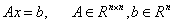
编制一个能自动选取主元,又能手动选取主元的求解线性方程组的Gauss消去过程。
实验要求:
(1)取矩阵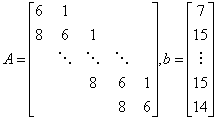 ,则方程有解
,则方程有解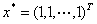 。取n=10计算矩阵的条件数。让程序自动选取主元,结果如何?
。取n=10计算矩阵的条件数。让程序自动选取主元,结果如何?
(2)现选择程序中手动选取主元的功能。每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。
(4)选取其他你感兴趣的问题或者随机生成矩阵,计算其条件数。重复上述实验,观察记录并分析实验结果。
实验过程:
实验代码:
建立M文件:
function x=gauss(n,r)
n=input('请输入矩阵A的阶数:n=')
A=diag(6*ones(1,n))+diag(ones(1,n-1),1)+diag(8*ones(1,n-1),-1)
b=A*ones(n,1)
p=input('条件数对应的范数是p-范数:p=')
pp=cond(A,p)
pause
[m,n]=size(A);
nb=n+1;Ab=[A b]
r=input('请输入是否为手动,手动输入1,自动输入0:r=')
for i=1:n-1
if r==0
[pivot,p]=max(abs(Ab(i:n,i)));
ip=p+i-1;
if ip~=i
Ab([i ip],:)=Ab([ip i],:);disp(Ab); pause
end
end
if r==1
i=i
ip=input('输入i列所选元素所处的行数:ip=');
Ab([i ip],:)=Ab([ip i],:);disp(Ab); pause
end
pivot=Ab(i,i);
for k=i+1:n
Ab(k,i:nb)=Ab(k,i:nb)-(Ab(k,i)/pivot)*Ab(i,i:nb);
end
disp(Ab); pause
end
x=zeros(n,1);x(n)=Ab(n,nb)/Ab(n,n);
for i=n-1:-1:1
x(i)=(Ab(i,nb)-Ab(i,i+1:n)*x(i+1:n))/Ab(i,i);
end
实验结果及分析:
⑴取矩阵A的阶数:n=10,自动选取主元:
>> format long
>> gauss
请输入矩阵A的阶数:n=10
n = 10
条件数对应的范数是p-范数:p=1
p = 1
pp = 2.557500000000000e+003
请输入是否为手动,手动输入1,自动输入0:r=0
r = 0
⑵取矩阵A的阶数:n=10,手动选取主元:
①选取绝对值最大的元素为主元:
>> gauss
请输入矩阵A的阶数:n=10
n = 10
条件数对应的范数是p-范数:p=2
p = 2
pp= 1.727556024913903e+003
请输入是否为手动,手动输入1,自动输入0:r=1
r = 1
ans= 1 1 1 1 1 1 1 1 1 1
②选取绝对值最小的元素为主元:
>> gauss
请输入矩阵A的阶数:n=10
n = 10
条件数对应的范数是p-范数:p=2
p = 2
pp = 1.727556024913903e+003
请输入是否为手动,手动输入1,自动输入0:r=1
r = 1
ans =
1.00000000000000 1.00000000000000 1.00000000000000
1.00000000000000 1.00000000000000 1.00000000000000
0.99999999999999 1.00000000000001 0.99999999999998
1.00000000000003
⑶取矩阵A的阶数:n=20,手动选取主元:
① 选取绝对值最大的元素为主元:
>> gauss
请输入矩阵A的阶数:n=20
条件数对应的范数是p-范数:p=1
p = 1
pp = 2.621437500000000e+006
ans = 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
② 选取绝对值最小的元素为主元:
>> gauss
请输入矩阵A的阶数:n=20.
n = 20
条件数对应的范数是p-范数:p=2
p = 2
pp = 1.789670565881683e+006
请输入是否为手动,手动输入1,自动输入0:r=1
r = 1
ans =
1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000001 0.99999999999997 1.00000000000006
0.99999999999989 1.00000000000023 0.99999999999955
1.00000000000090 0.99999999999821 1.00000000000352
0.99999999999318 1.00000000001273 0.99999999997817
1.00000000002910
⑷将M文件中的第三行:
A=diag(6*ones(1,n))+diag(ones(1,n-1),1)+diag(8*ones(1,n-1),-1)
改为:
A=hilb(n)
①>> gauss
请输入矩阵A的阶数:n=7
n = 7
条件数对应的范数是p-范数:p=1
p = 1
pp = 9.851948872610030e+008
请输入是否为手动,手动输入1,自动输入0:r=1
r = 1
ans =
1.00000000000051 0.99999999997251 1.00000000031354
0.99999999864133 1.00000000268805 0.99999999754181
1.00000000084337
②>> gauss
请输入矩阵A的阶数:n=7
n = 7
条件数对应的范数是p-范数:p=2
p = 2
pp = 4.753673569067072e+008
请输入是否为手动,手动输入1,自动输入0:r=1
r = 1
ans =
0.99999999999869 1.00000000004337 0.99999999964299
1.00000000121143 0.99999999803038 1.00000000152825
0.99999999954491
该问题在主元选取与算出结果有着很大的关系,取绝对值大的元素作为主元比取绝对值小的元素作为主元时产生的结果比较准确,即选取绝对值小的主元时结果产生了较大的误差,条件数越大产生的误差就越大。
实验总结:
通过本次实验,在gauss消去法解线性方程组时,主元的选择与算法的稳定性有密切的联系,选取绝对值大的元素作为主元比绝对值小的元素作为主元时对结果产生的误差较小。条件数越大对用gauss消去法解线性方程组时,对结果产生的误差就越大。主元的选取与算法的稳定性有密切的联系,选取适当的主元有利于得出稳定的算法,在算法的过程中,选取绝对值较大的主元比选取绝对值较小的主元更有利于算法的稳定,选取绝对值最大的元素作为主元时,得出的结果相对较准确较稳定。条件数越小,对用这种方法得出的结果更准确。
实验5.2(线性代数方程组的性态与条件数的估计)
问题提出:理论上,线性代数方程组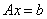 的摄动满足
的摄动满足
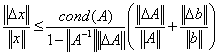
矩阵的条件数确实是对矩阵病态性的刻画,但在实际应用中直接计算它显然不现实,因为计算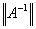 通常要比求解方程
通常要比求解方程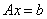 还困难。
还困难。
实验内容:MATLAB中提供有函数“condest”可以用来估计矩阵的条件数,它给出的是按1-范数的条件数。首先构造非奇异矩阵A和右端,使得方程是可以精确求解的。再人为地引进系数矩阵和右端的摄动 ,使得
,使得 充分小。
充分小。
实验要求:
(1)假设方程Ax=b的解为x,求解方程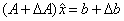 ,以1-范数,给出
,以1-范数,给出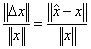 的计算结果。
的计算结果。
(2)选择一系列维数递增的矩阵(可以是随机生成的),比较函数“condest”所需机器时间的差别.考虑若干逆是已知的矩阵,借助函数“eig”很容易给出cond2(A)的数值。将它与函数“cond(A,2)”所得到的结果进行比较。
(3)利用“condest”给出矩阵A条件数的估计,针对(1)中的结果给出 的理论估计,并将它与(1)给出的计算结果进行比较,分析所得结果。注意,如果给出了cond(A)和
的理论估计,并将它与(1)给出的计算结果进行比较,分析所得结果。注意,如果给出了cond(A)和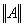 的估计,马上就可以给出
的估计,马上就可以给出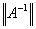 的估计。
的估计。
(4)估计著名的Hilbert矩阵的条件数。
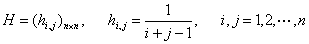
实验过程:
实验代码:
⑴
n=input('please input n:n=') %输入矩阵的阶数
a=fix(100*rand(n))+1 %随机生成一个矩阵a
x=ones(n,1) %假设知道方程组的解全为1
b=a*x %用矩阵a和以知解得出矩阵b
data=rand(n)*0.00001 %随即生成扰动矩阵data
datb=rand(n,1)*0.00001 %随即生成扰动矩阵datb
A=a+data
B=b+datb
xx=geshow(A,B) %解扰动后的解
x0=norm(xx-x,1)/norm(x,1) %得出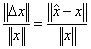 的理论结果
的理论结果
function x=geshow(A,B) %用高斯消去法解方程组
[m,n]=size(A);
nb=n+1;AB=[A B];
for i=1:n-1
pivot=AB(i,i);
for k=i+1:n
AB(k,i:nb)=AB(k,i:nb)-(AB(k,i)/pivot)*AB(i,i:nb);
end
end
x=zeros(n,1);
x(n)=AB(n,nb)/AB(n,n);
for i=n-1:-1:1
x(i)=(AB(i,nb)-AB(i,i+1:n)*x(i+1:n))/AB(i,i);
end
⑵
function cond2(A) %自定义求二阶条件数
B=A'*A;
[V1,D1]=eig(B);
[V2,D2]=eig(B^(-1));
cond2A=sqrt(max(max(D1)))*sqrt(max(max(D2)))
end
format long
for n=10:10:100
n=n %n为矩阵的阶
A=fix(100*randn(n)); %随机生成矩阵A
condestA=condest(A) %用condest求条件数
cond2(A) %用自定义的求条件数
condA2=cond(A,2) %用cond求条件数
pause %运行一次暂停
end
⑶
n=input('please input n:n=') %输入矩阵的阶数
a=fix(100*rand(n))+1; %随机生成一个矩阵a
x=ones(n,1); %假设知道方程组的解全为1
b=a*x; %用矩阵a和以知解得出矩阵b
data=rand(n)*0.00001; %随即生成扰动矩阵data
datb=rand(n,1)*0.00001; %随即生成扰动矩阵datb
A=a+data;
B=b+datb;
xx=geshow(A,B); %利用第一小问的geshow.m求出解阵
x0=norm(xx-x,1)/norm(x,1) %得出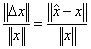 的理论结果
的理论结果
x00=cond(A)/(1-norm(inv(A))*norm(xx-x))*(norm((xx-x))/(norm(A))+norm(datb)/norm(B)) %得出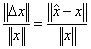 的估计值
的估计值
datx=abs(x0-x00) %求两者之间的误差
⑷
format long
for n=4:11
n=n %n为矩阵的阶数
Hi=hilb(n); %生成Hilbert矩阵
cond1Hi=cond(Hi,1) %求Hilbert矩阵得三种条件数
cond2Hi=cond(Hi,2)
condinfHi=cond(Hi,inf)
pause
end
实验结果及分析:
⑴>> fanshu
please input n:n=6
n =
6
a =
14 25 16 88 19 89
32 93 85 48 92 60
14 40 88 50 13 16
23 52 19 29 2 32
40 10 100 7 37 24
14 3 72 27 70 1
x =
1 1 1 1 1 1
b =
251 410 221 157 218 187
data =
1.0e-005 *
0.39690379186910 0.78196184196050 0.63712194084590 0.82064368228574 0.66093213223947 0.51488031898783
0.64986813059250 0.23756508204022 0.54592415509902 0.97047237460911 0.35801711338781 0.22157934638561
0.08500060621463 0.19573076378328 0.84805722441693 0.48692499554190 0.93819943010121 0.72500937095222
0.76880950325876 0.26321391517561 0.80209765848011 0.81746853554695 0.48766697476487 0.06824661097009
0.96970170497170 0.71378506459614 0.66830641006672 0.64157116784600 0.09099035774397 0.96412426837254
0.71479723187621 0.97759973943565 0.67098263396985 0.30634935951390 0.67383411686207 0.20765658836866
datb =
1.0e-005 *
0.16111822555138 0.63822138259275 0.00022817289162
0.33563294335217 0.27509982146621 0.04452752039203
A =
1.0e+002 *
0.14000003969038 0.25000007819618 0.16000006371219 0.88000008206437 0.19000006609321 0.89000005148803
0.32000006498681 0.93000002375651 0.85000005459242 0.48000009704724 0.92000003580171 0.60000002215793
0.14000000850006 0.40000001957308 0.88000008480572 0.50000004869250 0.13000009381994 0.16000007250094
0.23000007688095 0.52000002632139 0.19000008020977 0.29000008174685 0.02000004876670 0.32000000682466
0.40000009697017 0.10000007137851 1.00000006683064 0.07000006415712 0.37000000909904 0.24000009641243
0.14000007147972 0.03000009775997 0.72000006709826 0.27000003063494 0.70000006738341 0.01000002076566
B =
1.0e+002 *
2.51000001611182 4.10000006382214 2.21000000002282
1.57000003356329 2.18000002750998 1.87000000445275
xx =
0.99999830779720 1.00000022569555 1.00000019341555
0.99999909388073 0.99999996894021 1.00000066032794
x0 =
6.181368174725440e-007
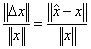 的计算结果为:6.181368174725440e-007
的计算结果为:6.181368174725440e-007
(2)
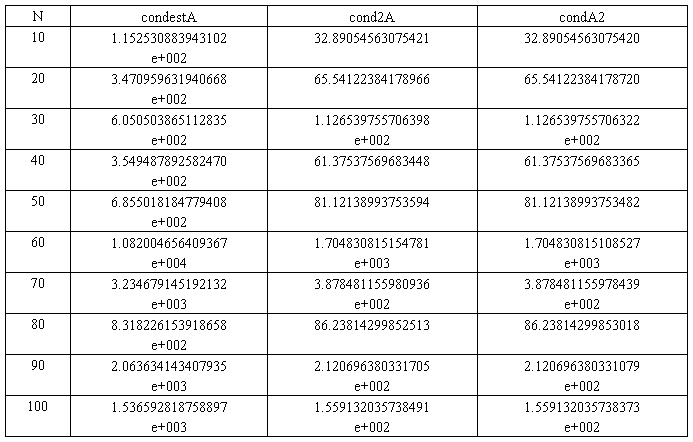
⑶
>> sy5_2
please input n:n=8
n = 8
x0 = 1.095033343195828e-006
x00 = 1.705456352162135e-005
datx = 1.595953017842553e-005
给出对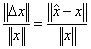 的估计是:1.705456352162135e-005
的估计是:1.705456352162135e-005
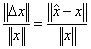 的理论结果是: 1.095033343195828e-006
的理论结果是: 1.095033343195828e-006
结果相差: 1.595953017842553e-005
(4)
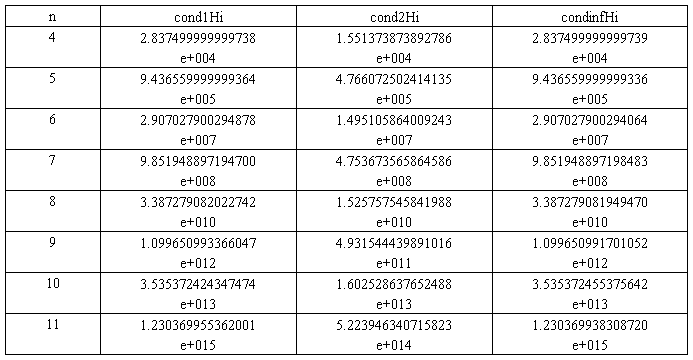
实验总结:
在本次实验中,使我们知道线性代数方程组的性态与条件数有着很重要的关系,既矩阵的条件数是刻画矩阵性质的一个重要的依据,条件数越大,矩阵“病态”性越严重,在解线性代数方程组的过程中较容易产生比较大的误差,则在实际问题的操作过程中,我们必须要减少对条件数来求解,把条件数较大的矩阵化成条件数较小的矩阵来进行求解。
实验六解线性方程组的迭代法
实验6.1(病态的线性方程组的求解)
问题提出:理论的分析表明,求解病态的线性方程组是困难的。实际情况是否如此,会出现怎样的现象呢?
实验内容:考虑方程组Hx=b的求解,其中系数矩阵H为Hilbert矩阵,
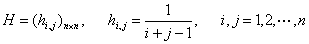
这是一个著名的病态问题。通过首先给定解(例如取为各个分量均为1)再计算出右端b的办法给出确定的问题。
实验要求:
(1)选择问题的维数为6,分别用Gauss消去法、J迭代法、GS迭代法和SOR迭代法求解方程组,其各自的结果如何?将计算结果与问题的解比较,结论如何?
(2)逐步增大问题的维数,仍然用上述的方法来解它们,计算的结果如何?计算的结果说明了什么?
(3)讨论病态问题求解的算法
Gauss消去法实验代码:
n=input('系数矩阵的阶数:');
A=hilb(n);%构造Hilbert矩阵
if a==0;
for i=1:(n-1);
for j=(i+1):n;
x=A(j,i)/A(i,i);
for k=1:(n+1);
A(j,k)=A(j,k)-x*A(i,k);
end;
end;
end;
y(n)=A(n,n+1)/A(n,n);
for i=2:n;
y(n-i+1)=A(n-i+1,n+1);
for j=1:(i-1);
y(n-i+1)=y(n-i+1)-A(n-i+1,n-j+1)*y(n-j+1);
end;
y(n-i+1)=y(n-i+1)/A(n-i+1,n-i+1);
end;
y
end;
%手动控制消元次序
if a==1;
for i=1:(n-1);
A %显示每步消元的结果
m=input('请选取作为主消元行的行号');
for l=1:(n+1);
c=A(i,l);
A(i,l)=A(m,l);
A(m,l)=c;
end;
for j=(i+1):n;
x=A(j,i)/A(i,i);
for k=1:(n+1);
A(j,k)=A(j,k)-x*A(i,k);
end;
end;
end;
y(n)=A(n,n+1)/A(n,n);
for i=2:n;
y(n-i+1)=A(n-i+1,n+1);
for j=1:(i-1);
y(n-i+1)=y(n-i+1)-A(n-i+1,n-j+1)*y(n-j+1);
end;
y(n-i+1)=y(n-i+1)/A(n-i+1,n-i+1);
end;
y
end;
J迭代法实验代码:
n=input('系数矩阵的阶数:');
A=hilb(n);%构造Hilbert矩阵
for i=1:n;
a0(i)=1; %给定解
x(i)=0;
end;
b=A*a0'; %由给定的解算出相应的b
%进行迭代
for i=1:100;
y=x;
for j=1:n;
x(j)=b(j)/A(j,j);
for k=1:j-1;
x(j)=x(j)-A(j,k)*y(k)/A(j,j);
end;
for k=j+1:n;
x(j)=x(j)-A(j,k)*y(k)/A(j,j);
end;
end;
end;x
GS迭代实验代码:
n=input('系数矩阵的阶数:');
%对题中给定的矩阵进行消元
A2=hilb(n);
for i=1:n;
a02(i)=1;
x2(i)=0;
end;
b2=A2*a02';
for i=1:100000;
for j=1:n;
x2(j)=b2(j)/A2(j,j);
for k=1:j-1;
x2(j)=x2(j)-A2(j,k)*x2(k)/A2(j,j);
end;
for k=j+1:n;
x2(j)=x2(j)-A2(j,k)*x2(k)/A2(j,j);
end;
end;
end;x2
SOR迭代实验代码:
n=input('系数矩阵的阶数:');
ss=input('松弛因子:');
%对题中给定的矩阵进行消元
A3=hilb(n);
for i=1:n;
a03(i)=1;
x3(i)=0;
end;
b3=A3*a03';
for i=1:100000;
for j=1:n;
rc=x3(j);
x3(j)=b3(j)/A3(j,j);
for k=1:j-1;
x3(j)=x3(j)-A3(j,k)*x3(k)/A3(j,j);
end;
for k=j+1:n;
x3(j)=x3(j)-A3(j,k)*x3(k)/A3(j,j);
end;
x3(j)=(1-ss)*rc+ss*x3(j);
end;
end;x3
实验结果及分析:
给定各分量为1的解,计算出右端作为研究问题。
1 选择问题的维数为6时:
用Gauss消去法求得的解与精确解一致;
取初始向量为0,用J迭代方法迭代出现发散的不稳定现象,无法求解;用GS迭代方法迭代不发散,能求得解,但收敛非常缓慢,当迭代次数取得相当大(100000次)时解仍在精确解附近波动;用SOR迭代方法迭代不发散,能求得解,当松弛因子去1.25左右时收敛较GS迭代快一些,但仍非常缓慢。
2 选择问题的维数为20时:
用Gauss消去法求得的解与精确解相差很大,相差10的量级。
取初始向量为0,用J迭代方法迭代发散,无法求解;
取初始向量为0,用GS迭代方法迭代不发散,能求得解,但收敛非常缓慢,迭代100000次后,算得的值与精确值1相差0.001的量级。
取初始向量为0,用SOR迭代方法迭代不发散,能求得解,但收敛非常缓慢。
从上面的结果可以看出当病态问题的阶数升高时作为直接法的Gauss消去法又能求解变成不能求解。而GS和SOR迭代法在阶数升高时仍能求解。但在阶数较低时直接法能求得精确解而迭代发却总存在一定的误差。可见直接法与迭代法各有各的优势与不足。
3 关于病态问题的求解,找到可逆的对角阵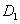 和
和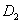 使方程组
使方程组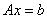 化为
化为 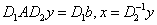 理论上最好选择对角阵
理论上最好选择对角阵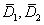 满足:
满足: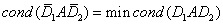 。
。
实验七 非线性方程求根
实验7.1(迭代法、初始值与收敛性)
实验目的:初步认识非线性问题的迭代法与线性问题迭代法的差别,探讨迭代法及初始值与迭代收敛性的关系。
问题提出:迭代法是求解非线性方程的基本思想方法,与线性方程的情况一样,其构造方法可以有多种多样,但关键是怎样才能使迭代收敛且有较快的收敛速度。
实验内容:考虑一个简单的代数方程
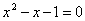
针对上述方程,可以构造多种迭代法,如



在实轴上取初始值x0,请分别用迭代(7.1)-(7.3)作实验,记录各算法的迭代过程。
实验要求:
(1)取定某个初始值,分别计算(7.1)-(7.3)迭代结果,它们的收敛性如何?重复选取不同的初始值,反复实验。请自选设计一种比较形象的记录方式(如利用MATLAB的图形功能),分析三种迭代法的收敛性与初值选取的关系。
(2)对三个迭代法中的某个,取不同的初始值进行迭代,结果如何?试分析迭代法对不同的初值是否有差异?
(3)线性方程组迭代法的收敛性是不依赖初始值选取的。比较线性与非线性问题迭代的差异,有何结论和问题。
相关MATLAB函数提示:

实验过程:
程序:
clear
clc
s=input('请输入要运行的方程,运行第几个输入几s=');
clf
if s==1 %决定坐标轴的范围和初始值
a=-1.5;b=2.5; y00=0; x00=input('请输入第一个函数的初值:x00=');
elseif s==2
a=0.1;b=6.5; y00=0; x00=input('请输入第二个函数的初值:x00=');
elseif s==3
a=0;b=2; y00=0; x00=input('请输入第三个函数的初值:x00=');
end
x=linspace(a,b,80);
y0=x; %计算直线y=x
y1=zxy7f(x,s); %计算迭代函数y=f(x)
clear y;
y=[y0;y1];
if s==1 %画图
plot(x,y,'linewidth',1)
legend('y=x','y=f1')
title('x(n+1)=[x(n)]^2-1') %输出标题
elseif s==2
plot(x,y,'linewidth',2)
legend('y=x','y=f2')
title('x(n+1)=1+1/x(n)')
elseif s==3
plot(x,y,'linewidth',3)
legend('y=x','y=f3')
title('x(n+1)=sqrt[x(n)+1]')
end
hold on
plot([a b],[0,0],'k-',[0 0],[a b],'k-')
axis([a,b,a,b]) %画坐标轴
z=[];
for i=1:15 %画蛛网图,迭代过程为n=15次
xt(1)=x00;yt(1)=y00; %决定始点坐标
xt(2)=zxy7f(xt(1),s); %决定终点坐标
yt(2)=zxy7f(xt(1),s);
zxyplot7(xt,yt,0.6) %画蛛网图
if i<=5
pause %按任意键逐次观察前5次迭代的蛛网图
end
x00=xt(2);y00=yt(2); %将本次迭代的终点作为下次的始点
z=[z,xt(1)]; %保存迭代点
end
function y=zxy7f(x,s)
if s==1
y=(x.*x-1);
elseif s==2
y=(1+1./x);
elseif s==3
y=sqrt(x+1);
end
function out=zxyplot7(x,y,p)%画一次迭代的蛛网图,改变p调节箭头的大小
u(1)=0;v(1)=(y(2)-y(1)); %画出始点(x(1),y(1))终点(x(2),y(2))的有向折线段
u(2)=eps;v(2)=eps;
h=quiver([x(1) x(1)],
[y(1) y(2)],u,v,p);
set(h,'color','red');
hold on
u(1)=(x(2)-x(1));v(1)=0;
u(2)=eps;v(2)=eps;
h=quiver([x(1) x(2)],
[y(2) y(2)],u,v,p);
set(h,'color','red');
plot([x(1) x(1) x(2)],[y(1) y(2) y(2)],'r.-')
数值实验结果及分析:
对于第一个迭代方程
x00=1.5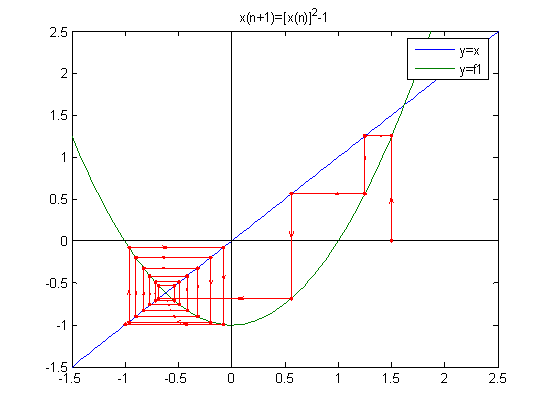
x00=0.5
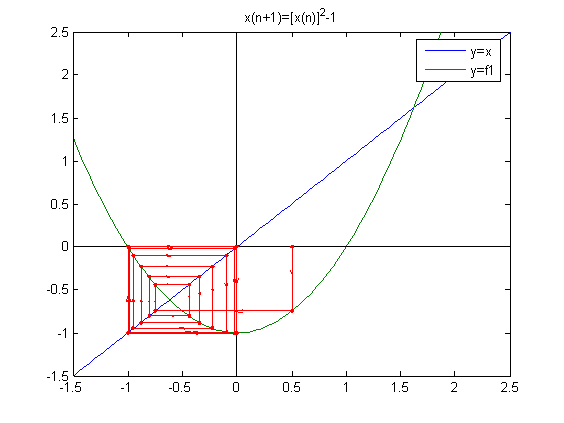 x00=0.8
x00=0.8 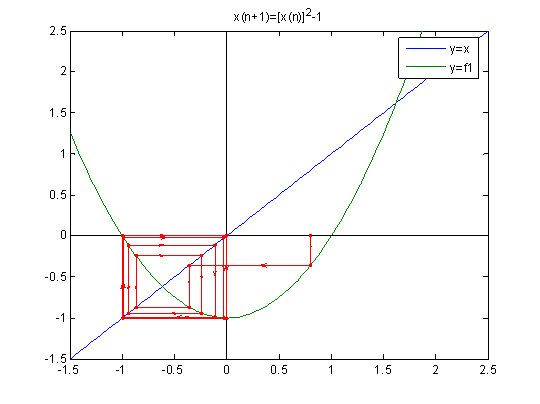
x00=1.2

对于第二个迭代方程
x00=0.5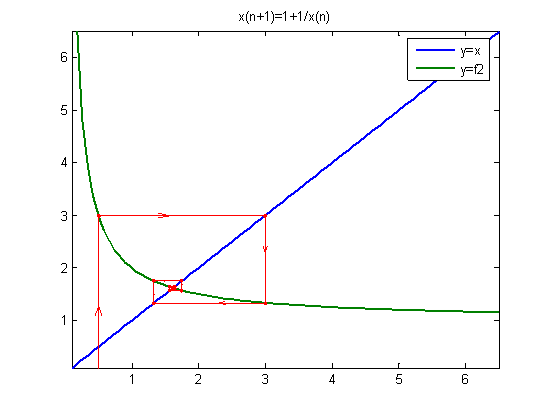
x00=3.0
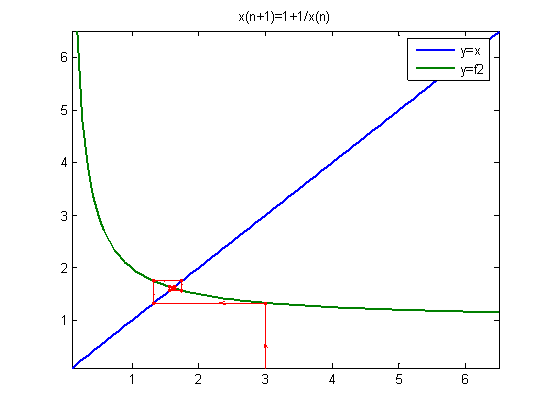
x00=0.2 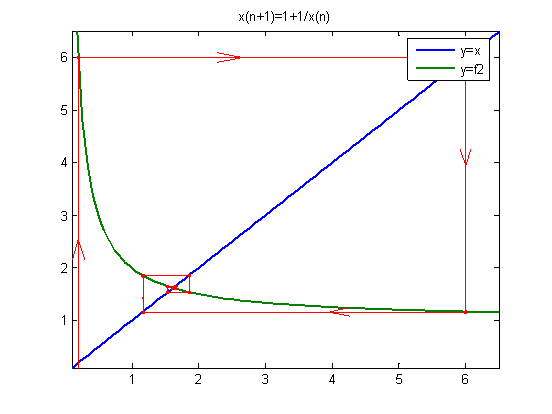
x00=5.0

对于第三个迭代方程
x00=0.2 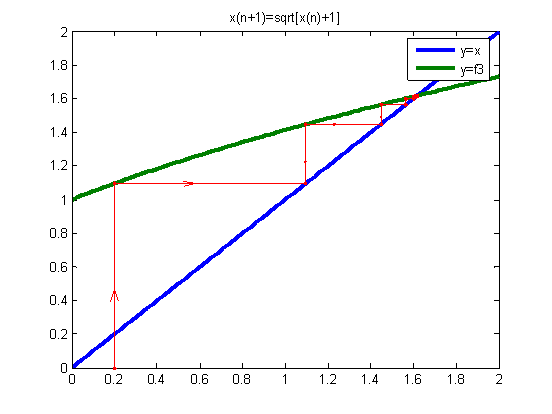
x00=1.0
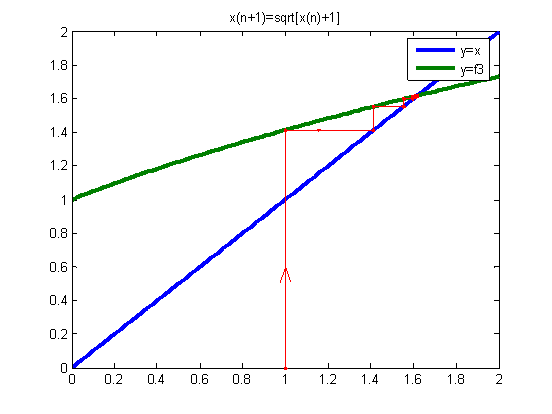
x00=0.6 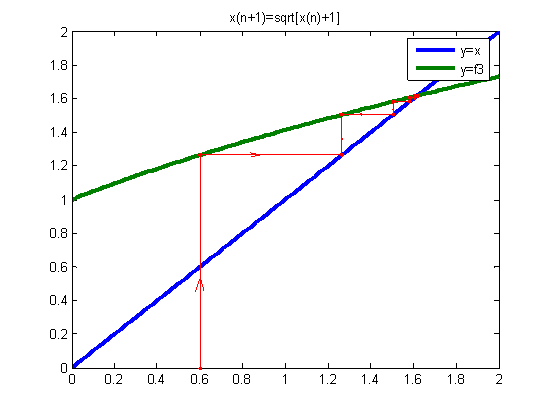
x00=1.4
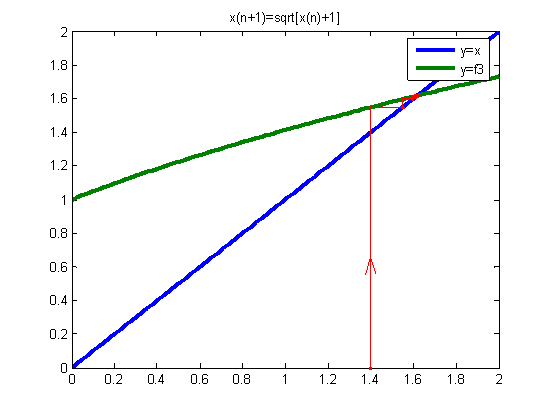
实验结果:
由上图可知,迭代方程收敛性与迭代方程的曲线的斜率有关,斜率越小的收敛性就越好,收敛速度越快,得到真解所需要的迭代数就越少;对同一个迭代方程取不同的初始值,对迭代方程的收敛速度也有一定的影响。
对于解线性方程组用迭代法的收敛性,取决于迭代方法的系数矩阵的普半径的大小,普半径小于1就收敛,于初值的选取无关,而对于解非线性方程的根用迭代法求解的收敛性取决于迭代方程的斜率,取定初始点的斜率小于1就收敛,于初值的选取有关。对于非线性方程的迭代法求根,有多种迭代方法,适当的选取迭代方程和适合的初值,有利于提高迭代方程的迭代速度,减少计算量。
