高考二轮小专题:圆锥曲线题型归纳
基础知识:
1.直线与圆的方程; 2.椭圆、双曲线、抛物线的定义与标准方程公式;
3.椭圆、双曲线、抛物线的几何性质等相关知识: 、
、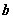 、
、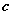 、
、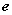 、
、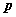 、渐近线。
、渐近线。
基本方法:
1. 待定系数法:求所设直线方程中的系数,求标准方程中的待定系数 、
、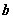 、
、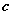 、
、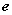 、
、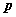 等等;
等等;
2. 齐次方程法:解决求离心率、渐近线、夹角等与比值有关的问题;
3. 韦达定理法:直线与曲线方程联立,交点坐标设而不求,用韦达定理写出转化完成。要注意:如果方程的根很容易求出,就不必用韦达定理,而直接计算出两个根;
4. 点差法:弦中点问题,端点坐标设而不求。也叫五条等式法:点满足方程两个、中点坐标公式两个、斜率公式一个共五个等式;
5. 距离转化法:将斜线上的长度问题、比例问题、向量问题转化水平或竖直方向上的距离问题、比例问题、坐标问题;
基本思想:
1.“常规求值”问题需要找等式,“求范围”问题需要找不等式;
2.“是否存在”问题当作存在去求,若不存在则计算时自然会无解;
3.证明“过定点”或“定值”,总要设一个或几个参变量,将对象表示出来,再说明与此变量无关;
4.证明不等式,或者求最值时,若不能用几何观察法,则必须用函数思想将对象表示为变量的函数,再解决;
5.有些题思路易成,但难以实施。这就要优化方法,才能使计算具有可行性,关键是积累“转化”的经验;
6.大多数问题只要忠实、准确地将题目每个条件和要求表达出来,即可自然而然产生思路。
一、求直线、圆锥曲线方程、离心率、弦长、渐近线等常规问题
例. 【浙江理数】设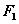 、
、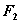 分别为双曲线
分别为双曲线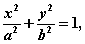 (
( >0、
>0、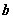 >0)的左、右焦点.若在双曲线右支上存在点
>0)的左、右焦点.若在双曲线右支上存在点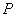 ,满足
,满足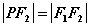 ,且
,且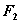 到直线
到直线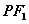 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
A.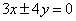 B.
B.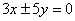 C.
C.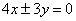 D.
D. 【答案】C
【答案】C
例. 【辽宁文数】设双曲线的一个焦点为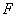 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线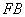 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A.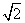 B.
B.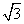 C.
C.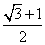 D.
D.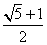 【答案】D
【答案】D
例.(14分)已知椭圆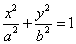
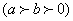 .过点(2,—1)且方向向量为
.过点(2,—1)且方向向量为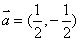 的直线L交椭圆与A、B两点。
的直线L交椭圆与A、B两点。
⑴若线段AB的中点为M,求直线OM的斜率(用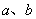 表示);
表示);
⑵若椭圆的离心率为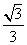 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
⑶在⑵的条件下,设椭圆的左焦点为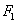 ,求
,求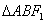 的面积。
的面积。
点评:常规求值问题的方法:待定系数法,先设后求,关键在于找等式。
二、“是否存在”问题
例.(14分)已知定点A(-2,-4),过点A作倾斜角为45度的直线L,交抛物线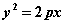 (
(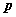 >0)于B、C两点,且线段BC长为
>0)于B、C两点,且线段BC长为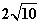 。
。
(I)求抛物线的方程;
(II)在(I)中的抛物线上是否存在点D,使得DB=DC成立?若存在,求出点D的坐标,若不存在,请说明理由。
(答: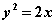 。存在点D(2,2)或(8,-4))
。存在点D(2,2)或(8,-4))
例. 【北京理数】在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于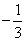 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
三、过定点、定值问题
例、(14分)已知抛物线S的顶点在坐标原点,焦点在x轴上,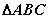 的三个顶点都在抛物线上,且
的三个顶点都在抛物线上,且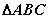 的重心为抛物线的焦点,若BC所在直线L的方程为4x+y-20=0.
的重心为抛物线的焦点,若BC所在直线L的方程为4x+y-20=0.
(Ⅰ)求抛物线S的方程;
(Ⅱ)若O是坐标原点,P、Q是抛物线S上的两动点,且满足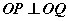 。试说明动直线PQ是否过一个定点。
。试说明动直线PQ是否过一个定点。
(答: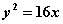 ,定点为M(16,0))
,定点为M(16,0))
例.(14分)已知椭圆C: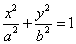 (
(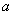 >
> >0),过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形。
>0),过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)过点Q(—1,0)的直线L交椭圆于A、B两点,交直线x = —4于点E,设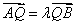 ,
,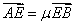 。求证:
。求证: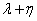 为定值,并计算出该定值。
为定值,并计算出该定值。
点评:距离转化法把斜线上的转化为垂直与水平上的,比如向量中的比例以坐标转化,比如抛物线中焦半径与到准线距离的转化。
例.(14分)过抛物线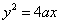 (
(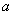 >0)的焦点F作任意一条直线分别交抛物线于A、B两点,如果
>0)的焦点F作任意一条直线分别交抛物线于A、B两点,如果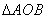 (O为原点)的面积是S,求证:
(O为原点)的面积是S,求证: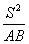 为定值。(答:
为定值。(答: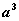 )
)
点评:证明定值问题的方法:⑴常把变动的元素用参数表示出来,然后证明计算结果与参数无关;⑵也可先在特殊条件下求出定值,再给出一般的证明。
处理定点问题的方法:⑴常把方程中参数的同次项集在一起,并令各项的系数为零,求出定点;⑵也可先取参数的特殊值探求定点,然后给出证明。
四.最值问题
例.(14分)定长为3的线段AB的两个端点在抛物线 上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的纵坐标。(答:最短距离为
上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的纵坐标。(答:最短距离为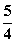 ,M的纵坐标为
,M的纵坐标为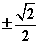 )
)
点评:最值问题的方法:几何法、配方法(转化为二次函数的最值)、三角代换法(转化为三角函数的最值)、利用切线的方法、利用均值不等式的方法等。
五、求参数范围问题。
常用思路:寻找不等式。将各限制条件都列出,再求交集。不要遗漏限制条件。
常用建立不等式的途径:
(1) 直线与曲线有交点时判别式大于等于零;
⑵ 圆锥曲线中变量X、Y的取值范围;
⑶ 点与曲线的位置关系,如弦的中点在曲线内部;
⑷ 已知题设中有的范围;
⑸ 正弦函数、余弦函数的有界性;
⑹ 均值不等式;
⑺ 焦半径的取值范围;
⑻ 函数的值域;
⑼ 三角形图形中两边之和大于第三边。
例:1.若直线y=kx+1与焦点在x轴上的椭圆 恒有公共点,则t的取值范围为_________.(答:
恒有公共点,则t的取值范围为_________.(答: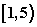
2.【福建文数】若点O和点F分别为椭圆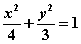 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则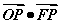 的最大值为( )
的最大值为( )
A.2 B.3 C.6 D.8 【答案】C(利用圆锥曲线中变量X、Y的取值范围;)
3.设 >1,则双曲线
>1,则双曲线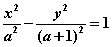 的离心率e的取值范围为_________;(答:
的离心率e的取值范围为_________;(答: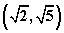 )
)
4.若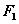 、
、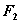 是双曲线
是双曲线 的左右焦点,过
的左右焦点,过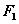 作垂直于x轴的直线交双曲线于A、B两点,若
作垂直于x轴的直线交双曲线于A、B两点,若 为锐角三角形,则双曲线的离心率的取值范围为____________;(答:
为锐角三角形,则双曲线的离心率的取值范围为____________;(答: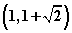 )
)
5.若M是椭圆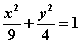 上的任意一点,
上的任意一点,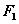 、
、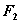 是椭圆的左、右焦点,则
是椭圆的左、右焦点,则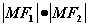 的最大值为____;(答:9)(利用均值不等式)
的最大值为____;(答:9)(利用均值不等式)
6.若点P是抛物线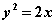 上的一个动点,则点P到点(0,2)的距离与点P到准线的距离之和的最小值为__________;(答:
上的一个动点,则点P到点(0,2)的距离与点P到准线的距离之和的最小值为__________;(答: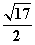 )(利用三角形两边之和大于第三边)
)(利用三角形两边之和大于第三边)
六、规范解题
解析几何在高考中经常是两小题一大题:两小题经常是常规求值类型,一大题中的第一小题也经常是常规求值问题,故常用方程思想先设后求即可。解决第二小题时常用韦达定理法结合以上各种题型进行处理,常按照以下七步骤:
一设直线与方程;(提醒:①设直线时分斜率存在与不存在;②设为y=kx+b与x=mmy+n的区别)二设交点坐标;(提醒:之所以要设是因为不去求出它,即“设而不求”)
三则联立方程组;四则消元韦达定理;(提醒:抛物线时经常是把抛物线方程代入直线方程反而简单)五根据条件重转化;常有以下类型:
①“以弦AB为直径的圆过点0”
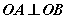

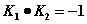 (提醒:需讨论K是否存在)
(提醒:需讨论K是否存在)
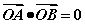

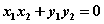
②“点在圆内、圆上、圆外问题” “直角、锐角、钝角问题”
“直角、锐角、钝角问题”
 “向量的数量积大于、等于、小于0问题”
“向量的数量积大于、等于、小于0问题”
 >0;
>0;
③“等角、角平分、角互补问题” 斜率关系(
斜率关系(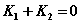 或
或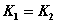 );
);
④“共线问题”(如: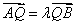
 数的角度:坐标表示法;形的角度:距离转化法);
数的角度:坐标表示法;形的角度:距离转化法);
(如:A、O、B三点共线 直线OA与OB斜率相等);
直线OA与OB斜率相等);
⑤“点、线对称问题”  坐标与斜率关系;⑥“弦长、面积问题”
坐标与斜率关系;⑥“弦长、面积问题”
 转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);六则化简与计算;
转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);六则化简与计算;
七则细节问题不忽略;①判别式是否已经考虑;②抛物线问题中二次项系数是否会出现0.
七、站在系统的高度探究问题的本原
“直线与圆锥曲线的位置关系”中文科主要考察“直线与抛物线”,这里就仅举直线与抛物线的位置关系为例。
请证明以下命题:
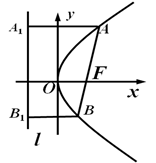
案例一:抛物线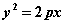 (
(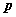 >0),过焦点F(
>0),过焦点F(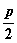 ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A( ,
,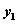 )、B(
)、B(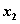 ,
, )。如图
)。如图
(一) 有关定值问题:
 (1)
(1)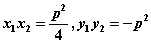 ;
;
(2)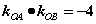
(3)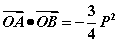
(4) ;
;
(5)过抛物线的焦点作两条垂直的弦AB,CD,则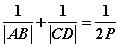 ;
;
(二) 与数列有关的问题
(1) AB为焦点弦,T为准线上任意一点,则TA、TF、TB的斜率成等差数列;
(2) AB为焦点弦,过点A、B的切线相交于点M,则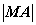 、
、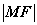 、
、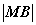 成等比数列;
成等比数列;
(三) 有关圆的问题
(1) 以AB为直径的圆与抛物线的准线相切;以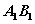 为直径的圆与抛物线的弦AB相切;
为直径的圆与抛物线的弦AB相切;
(2) 以AF为直径的圆与y轴相切;以BF为直径的圆与y轴相切;
(3) 其中性质(1) 抛物线的准线与x轴的交点E在以AB为直径的圆外。
抛物线的准线与x轴的交点E在以AB为直径的圆外。
(四) 有关共线问题
(1)A、O、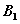 三点共线; (2)B、O、
三点共线; (2)B、O、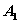 三点共线;
三点共线;
(五) 有关平分问题:
EF平分

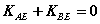
(六) 有关面积问题
(1)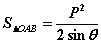 ; (2)
; (2)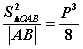 ;(3)
;(3)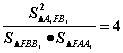 ;
;
(七)有关定点问题
符合以上任一条性质的弦AB过一定点F(即抛物线的焦点)。
案例二:抛物线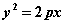 (
(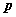 >0),过点
>0),过点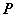 (
(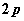 ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A( ,
,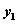 )、B(
)、B(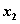 ,
,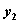 )。则
)。则
(一)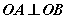 ;
;
(二)以AB为直径的圆经过原点;
(三)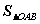 的最小值为
的最小值为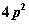 ,此时
,此时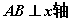 ;
;
(四)当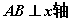 时,以AB为直径的圆的面积最小;
时,以AB为直径的圆的面积最小;
(五)过O作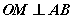 ,垂足为M,则M点必在一个圆的圆周上;(答:
,垂足为M,则M点必在一个圆的圆周上;(答: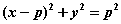 ,除原点外);
,除原点外);
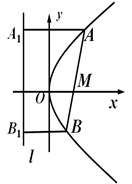 案例三:抛物线
案例三:抛物线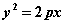 (
(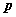 >0),过点M(
>0),过点M(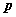 ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A( ,
,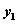 )、B(
)、B(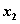 ,
,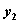 )。
)。
(一) ;
;
(二)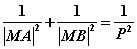 ;
;
(三)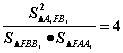 。
。
第二篇:高考二轮小专题_:圆锥曲线题型归纳精品2
各位教师,同学,我精心汇总,好好利用
高考二轮小专题:圆锥曲线题型归纳
基础知识:
1.直线与圆的方程; 2.椭圆、双曲线、抛物线的定义与标准方程公式;
3.椭圆、双曲线、抛物线的几何性质等相关知识: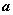 、
、 、
、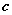 、
、 、
、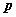 、渐近线。
、渐近线。
基本方法:
1. 待定系数法:求所设直线方程中的系数,求标准方程中的待定系数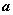 、
、 、
、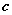 、
、 、
、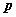 等等;
等等;
2. 齐次方程法:解决求离心率、渐近线、夹角等与比值有关的问题;
3. 韦达定理法:直线与曲线方程联立,交点坐标设而不求,用韦达定理写出转化完成。要注意:如果方程的根很容易求出,就不必用韦达定理,而直接计算出两个根;
4. 点差法:弦中点问题,端点坐标设而不求。也叫五条等式法:点满足方程两个、中点坐标公式两个、斜率公式一个共五个等式;
5. 距离转化法:将斜线上的长度问题、比例问题、向量问题转化水平或竖直方向上的距离问题、比例问题、坐标问题;
基本思想:
1.“常规求值”问题需要找等式,“求范围”问题需要找不等式;
2.“是否存在”问题当作存在去求,若不存在则计算时自然会无解;
3.证明“过定点”或“定值”,总要设一个或几个参变量,将对象表示出来,再说明与此变量无关;
4.证明不等式,或者求最值时,若不能用几何观察法,则必须用函数思想将对象表示为变量的函数,再解决;
5.有些题思路易成,但难以实施。这就要优化方法,才能使计算具有可行性,关键是积累“转化”的经验;
6.大多数问题只要忠实、准确地将题目每个条件和要求表达出来,即可自然而然产生思路。
一、求直线、圆锥曲线方程、离心率、弦长、渐近线等常规问题
例. 【浙江理数】设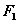 、
、 分别为双曲线
分别为双曲线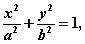 (
(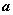 >0、
>0、 >0)的左、右焦点.若在双曲线右支上存在点
>0)的左、右焦点.若在双曲线右支上存在点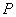 ,满足
,满足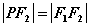 ,且
,且 到直线
到直线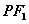 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
A. B.
B.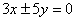 C.
C.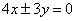 D.
D.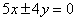 【答案】C
【答案】C
例. 【辽宁文数】设双曲线的一个焦点为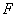 ,虚轴的一个端点为
,虚轴的一个端点为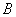 ,如果直线
,如果直线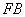 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A.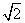 B.
B. C.
C. D.
D.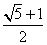 【答案】D
【答案】D
例.(14分)已知椭圆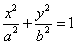
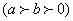 .过点(2,—1)且方向向量为
.过点(2,—1)且方向向量为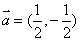 的直线L交椭圆与A、B两点。
的直线L交椭圆与A、B两点。
⑴若线段AB的中点为M,求直线OM的斜率(用 表示);
表示);
⑵若椭圆的离心率为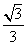 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
⑶在⑵的条件下,设椭圆的左焦点为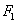 ,求
,求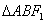 的面积。
的面积。
点评:常规求值问题的方法:待定系数法,先设后求,关键在于找等式。
二、“是否存在”问题
例.(14分)已知定点A(-2,-4),过点A作倾斜角为45度的直线L,交抛物线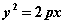 (
(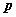 >0)于B、C两点,且线段BC长为
>0)于B、C两点,且线段BC长为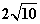 。
。
(I)求抛物线的方程;
(II)在(I)中的抛物线上是否存在点D,使得DB=DC成立?若存在,求出点D的坐标,若不存在,请说明理由。
(答: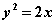 。存在点D(2,2)或(8,-4))
。存在点D(2,2)或(8,-4))
例. 【北京理数】在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
三、过定点、定值问题
例、(14分)已知抛物线S的顶点在坐标原点,焦点在x轴上,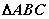 的三个顶点都在抛物线上,且
的三个顶点都在抛物线上,且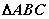 的重心为抛物线的焦点,若BC所在直线L的方程为4x+y-20=0.
的重心为抛物线的焦点,若BC所在直线L的方程为4x+y-20=0.
(Ⅰ)求抛物线S的方程;
(Ⅱ)若O是坐标原点,P、Q是抛物线S上的两动点,且满足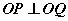 。试说明动直线PQ是否过一个定点。
。试说明动直线PQ是否过一个定点。
(答: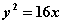 ,定点为M(16,0))
,定点为M(16,0))
例.(14分)已知椭圆C: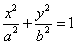 (
(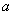 >
>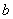 >0),过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形。
>0),过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)过点Q(—1,0)的直线L交椭圆于A、B两点,交直线x = —4于点E,设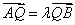 ,
,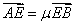 。求证:
。求证: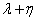 为定值,并计算出该定值。
为定值,并计算出该定值。
点评:距离转化法把斜线上的转化为垂直与水平上的,比如向量中的比例以坐标转化,比如抛物线中焦半径与到准线距离的转化。
例.(14分)过抛物线 (
(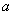 >0)的焦点F作任意一条直线分别交抛物线于A、B两点,如果
>0)的焦点F作任意一条直线分别交抛物线于A、B两点,如果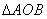 (O为原点)的面积是S,求证:
(O为原点)的面积是S,求证: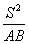 为定值。(答:
为定值。(答: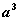 )
)
点评:证明定值问题的方法:⑴常把变动的元素用参数表示出来,然后证明计算结果与参数无关;⑵也可先在特殊条件下求出定值,再给出一般的证明。
处理定点问题的方法:⑴常把方程中参数的同次项集在一起,并令各项的系数为零,求出定点;⑵也可先取参数的特殊值探求定点,然后给出证明。
四.最值问题
例.(14分)定长为3的线段AB的两个端点在抛物线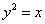 上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的纵坐标。(答:最短距离为
上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的纵坐标。(答:最短距离为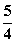 ,M的纵坐标为
,M的纵坐标为 )
)
点评:最值问题的方法:几何法、配方法(转化为二次函数的最值)、三角代换法(转化为三角函数的最值)、利用切线的方法、利用均值不等式的方法等。
五、求参数范围问题。
常用思路:寻找不等式。将各限制条件都列出,再求交集。不要遗漏限制条件。
常用建立不等式的途径:
(1) 直线与曲线有交点时判别式大于等于零;
⑵ 圆锥曲线中变量X、Y的取值范围;
⑶ 点与曲线的位置关系,如弦的中点在曲线内部;
⑷ 已知题设中有的范围;
⑸ 正弦函数、余弦函数的有界性;
⑹ 均值不等式;
⑺ 焦半径的取值范围;
⑻ 函数的值域;
⑼ 三角形图形中两边之和大于第三边。
例:1.若直线y=kx+1与焦点在x轴上的椭圆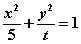 恒有公共点,则t的取值范围为_________.(答:
恒有公共点,则t的取值范围为_________.(答: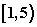
2.【福建文数】若点O和点F分别为椭圆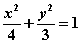 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则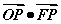 的最大值为( )
的最大值为( )
A.2 B.3 C.6 D.8 【答案】C(利用圆锥曲线中变量X、Y的取值范围;)
3.设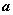 >1,则双曲线
>1,则双曲线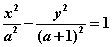 的离心率e的取值范围为_________;(答:
的离心率e的取值范围为_________;(答: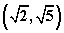 )
)
4.若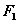 、
、 是双曲线
是双曲线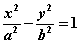 的左右焦点,过
的左右焦点,过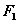 作垂直于x轴的直线交双曲线于A、B两点,若
作垂直于x轴的直线交双曲线于A、B两点,若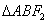 为锐角三角形,则双曲线的离心率的取值范围为____________;(答:
为锐角三角形,则双曲线的离心率的取值范围为____________;(答: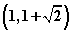 )
)
5.若M是椭圆 上的任意一点,
上的任意一点,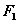 、
、 是椭圆的左、右焦点,则
是椭圆的左、右焦点,则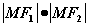 的最大值为____;(答:9)(利用均值不等式)
的最大值为____;(答:9)(利用均值不等式)
6.若点P是抛物线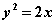 上的一个动点,则点P到点(0,2)的距离与点P到准线的距离之和的最小值为__________;(答:
上的一个动点,则点P到点(0,2)的距离与点P到准线的距离之和的最小值为__________;(答: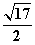 )(利用三角形两边之和大于第三边)
)(利用三角形两边之和大于第三边)
六、规范解题
解析几何在高考中经常是两小题一大题:两小题经常是常规求值类型,一大题中的第一小题也经常是常规求值问题,故常用方程思想先设后求即可。解决第二小题时常用韦达定理法结合以上各种题型进行处理,常按照以下七步骤:
一设直线与方程;(提醒:①设直线时分斜率存在与不存在;②设为y=kx+b与x=mmy+n的区别)二设交点坐标;(提醒:之所以要设是因为不去求出它,即“设而不求”)
三则联立方程组;四则消元韦达定理;(提醒:抛物线时经常是把抛物线方程代入直线方程反而简单)五根据条件重转化;常有以下类型:
①“以弦AB为直径的圆过点0”


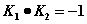 (提醒:需讨论K是否存在)
(提醒:需讨论K是否存在)


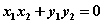
②“点在圆内、圆上、圆外问题” “直角、锐角、钝角问题”
“直角、锐角、钝角问题”
 “向量的数量积大于、等于、小于0问题”
“向量的数量积大于、等于、小于0问题”
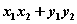 >0;
>0;
③“等角、角平分、角互补问题” 斜率关系(
斜率关系(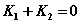 或
或 );
);
④“共线问题”(如: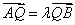
 数的角度:坐标表示法;形的角度:距离转化法);
数的角度:坐标表示法;形的角度:距离转化法);
(如:A、O、B三点共线 直线OA与OB斜率相等);
直线OA与OB斜率相等);
⑤“点、线对称问题”  坐标与斜率关系;⑥“弦长、面积问题”
坐标与斜率关系;⑥“弦长、面积问题”
 转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);六则化简与计算;
转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);六则化简与计算;
七则细节问题不忽略;①判别式是否已经考虑;②抛物线问题中二次项系数是否会出现0.
七、站在系统的高度探究问题的本原
“直线与圆锥曲线的位置关系”中文科主要考察“直线与抛物线”,这里就仅举直线与抛物线的位置关系为例。
请证明以下命题:
案例一:抛物线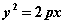 (
(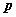 >0),过焦点F(
>0),过焦点F( ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A(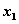 ,
,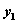 )、B(
)、B( ,
,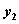 )。如图
)。如图
(一) 有关定值问题:
 (1)
(1) ;
;
(2)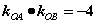
(3)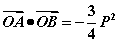
(4)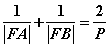 ;
;
(5)过抛物线的焦点作两条垂直的弦AB,CD,则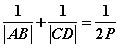 ;
;
(二) 与数列有关的问题
(1) AB为焦点弦,T为准线上任意一点,则TA、TF、TB的斜率成等差数列;
(2) AB为焦点弦,过点A、B的切线相交于点M,则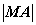 、
、 、
、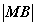 成等比数列;
成等比数列;
(三) 有关圆的问题
(1) 以AB为直径的圆与抛物线的准线相切;以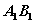 为直径的圆与抛物线的弦AB相切;
为直径的圆与抛物线的弦AB相切;
(2) 以AF为直径的圆与y轴相切;以BF为直径的圆与y轴相切;
(3) 其中性质(1) 抛物线的准线与x轴的交点E在以AB为直径的圆外。
抛物线的准线与x轴的交点E在以AB为直径的圆外。
(四) 有关共线问题
(1)A、O、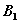 三点共线; (2)B、O、
三点共线; (2)B、O、 三点共线;
三点共线;
(五) 有关平分问题:
EF平分

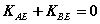
(六) 有关面积问题
(1)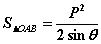 ; (2)
; (2)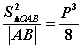 ;(3)
;(3)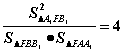 ;
;
(七)有关定点问题
符合以上任一条性质的弦AB过一定点F(即抛物线的焦点)。
案例二:抛物线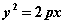 (
(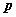 >0),过点
>0),过点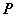 (
(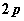 ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A(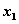 ,
,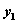 )、B(
)、B( ,
,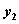 )。则
)。则
(一) ;
;
(二)以AB为直径的圆经过原点;
(三)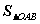 的最小值为
的最小值为 ,此时
,此时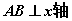 ;
;
(四)当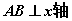 时,以AB为直径的圆的面积最小;
时,以AB为直径的圆的面积最小;
(五)过O作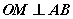 ,垂足为M,则M点必在一个圆的圆周上;(答:
,垂足为M,则M点必在一个圆的圆周上;(答: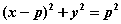 ,除原点外);
,除原点外);
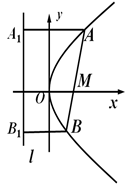 案例三:抛物线
案例三:抛物线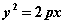 (
(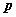 >0),过点M(
>0),过点M(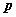 ,0)作一条弦AB交抛物线于A、B两点,其中A(
,0)作一条弦AB交抛物线于A、B两点,其中A(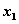 ,
,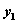 )、B(
)、B( ,
,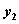 )。
)。
(一)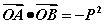 ;
;
(二)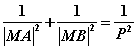 ;
;
(三)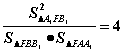 。
。
