圆锥曲线题型总结
高考圆锥曲线的七种题型;题型一:定义的应用;1、圆锥曲线的定义:;(1)椭圆;(2)椭圆;(3)椭圆;2、定义的应用;(1)寻找符合条件的等量关系;(2)等价转换,数形结合;3、定义的适用条件:;典型例题;例1、动圆M与圆C1:(x+1)+y=36内切,;例2、方程;题型二:圆锥曲线焦点位置的判断(首先化成标准方程;1、椭圆:由2、双曲线:由,,分母的大小决
高考圆锥曲线的七种题型
题型一:定义的应用
1、圆锥曲线的定义:
(1)椭圆
(2)椭圆
(3)椭圆
2、定义的应用
(1)寻找符合条件的等量关系
(2)等价转换,数形结合
3、定义的适用条件:
典型例题
例1、动圆M与圆C1:(x+1)+y=36内切,与圆C2:(x-1)+y=4外切,求圆心M的轨迹方程。
例2、方程
题型二:圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):
1、椭圆:由2、双曲线:由,,分母的大小决定,焦点在分母大的坐标轴上。 项系数的正负决定,焦点在系数为正的坐标轴上; 表示的曲线是 2222
3、抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
典型例题
x2y2
例1、已知方程??1表示焦点在y轴上的椭圆,则m的取值范围是 m?12?m
x2y2
??1的曲线: 例2、k为何值时,方程9?k5?k
(1)是椭圆;
(2)是双曲线.
题型三:圆锥曲线焦点三角形(椭圆或双曲线上的一点与两焦点所构成的三角形)问题
1、椭圆焦点三角形面积S?btan2?
2 ;双曲线焦点三角形面积S?bcot2?
2
2、常利用第一定义和正弦、余弦定理求解
3、m?n,m?n,mn,m2?n2四者的关系在圆锥曲线中的应用;
典型例题
22xy例1、椭圆22?,求1(a?b?0)上一点P与两个焦点FFPF?1,2的张角∠F12?ab
证:△F1PF2的面积为btan2?。
2
例2、已知双曲线的离心率为2,F1、F2是左右焦点,P为双曲线上一点,且
.求该双曲线的标准方程
题型四:圆锥曲线中离心率,渐近线的求法
1、a,b,c三者知道任意两个或三个的相等关系式,可求离心率,渐进线的值; ,
2、a,b,c三者知道任意两个或三个的不等关系式,可求离心率,渐进线的最值或范围;
3、注重数形结合思想不等式解法
典型例题
x2y2
例1、已知F1、F2是双曲线2?2?1(a?0,b?0)的两焦点,以线段F1F2为边作正ab
三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( ) A. 4?2 B. ?1 C.
?1 D. ?1
2
x2y2
例2、双曲线2?2?1(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,ab
则双曲线离心率的取值范围为
A. (1,3)
B.?1,3? C.(3,+?) D.?3,???
x2y2
例3、椭圆G:2?2?1(a?b?0)的两焦点为F1(?c,0),F2(c,0),椭圆上存在 ab
点M使F1M?F2M?0. 求椭圆离心率e的取值范围;
例4、已知双曲线2?2?1(a?0,b?0)的右焦点为F,若过点F且倾斜角为60?的直线 ab
与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(A)(1,2] (B)(1,2) (C)[2,??) (D)(2,??)
题型五:点、直线与圆锥的位置关系判断
1、点与椭圆的位置关系
x2y2
点在椭圆内?2?2?1 ab
x2y2
点在椭圆上?2?2?1 ab
2、直线与圆锥曲线有无公共点或有几个公共点的问题:
?>0?相交
?=0?相切 (需要注意二次项系数为0的情况)
?<0?相离
3、弦长公式: AB??k2x1?x2??k2(x1?x2)??k2? a
AB??111? y?y??(y?y)??1212222kkka
4、圆锥曲线的中点弦问题:
1、伟达定理:
2、点差法:
(1)带点进圆锥曲线方程,做差化简
(2)得到中点坐标比值与直线斜率的等式关系
典型例题
例1、双曲线x2-4y2=4的弦AB被点M(3,-1)平分,求直线AB的方程.
例2、已知中心在原点,对称轴在坐标轴上的椭圆与直线L:x+y=1交于A,B两点,C是AB的中点,若|AB|=22,O为坐标原点,OC的斜率为2/2,求椭圆的方程。
题型六:动点轨迹方程:
1、求轨迹方程的步骤:建系、设点、列式、化简、确定点的范围;
2、求轨迹方程的常用方法:
(1)直接法:直接利用条件建立之间的关系;
例1、如已知动点P到定点F(1,0)和直线
的距离之和等于4,求P的轨迹方程.
(2)待定系数法:已知所求曲线的类型,求曲线方程——先根据条件设出所求曲线的方程,再由条件确定其待定系数。
例2、如线段AB过x轴正半轴上一点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线,则此抛物线方程为
(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程;
例3、由动点P向圆作两条切线PA、PB,切点分别为A、B,∠APB=60,则动点0P的轨迹方程为
例4、点M与点F(4,0)的距离比它到直线
例5、一动圆与两圆⊙M:
的轨迹为
(4)代入转移法:动点
在某已知曲线上,则可先用迹方程:
例6、如动点P是抛物线则M的轨迹方程为__________
(5)
参数法:当动点
虑将
例7、过抛物线的焦点F作直线交抛物线于A、B两点,则弦AB的中点M的轨迹方坐标之间的关系不易直接找到,也没有相关动点可用时,可考上任一点,定点为,点M分所成的比为2,依赖于另一动点
的代数式表示的变化而变化,并且,再将又和⊙N:都外切,则动圆圆心的距离小于1,则点M的轨迹方程是_______ 代入已知曲线得要求的轨均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程)。 程是
题型七:(直线与圆锥曲线常规解题方法)
一、设直线与方程;(提醒:①设直线时分斜率存在与;二、设交点坐标;(提醒:之所以要设是因为不去求出;三、联立方程组;;四、消元韦达定理;(提醒:抛物线时经常是把抛物线;五、根据条件重转化;常有以下类型:;①“以弦AB为直径的圆过点0”(提醒:需讨论K是;?????????OA?OB?K1?K2??1?;②“点在圆内、圆上、圆外问题”;?“直角、锐角、钝角问题
一、设直线与方程;(提醒:①设直线时分斜率存在与不存在;②设为y=kx+b与x=my+n的区别)
二、设交点坐标;(提醒:之所以要设是因为不去求出它,即“设而不求”)
三、联立方程组;
四、消元韦达定理;(提醒:抛物线时经常是把抛物线方程代入直线方程反而简单)
五、根据条件重转化;常有以下类型:
①“以弦AB为直径的圆过点0”(提醒:需讨论K是否存在)
?????????OA?OB ?K1?K2??1 ?OA?OB?0 ? x1x2?y1y2?0
②“点在圆内、圆上、圆外问题”
?“直角、锐角、钝角问题” ?“向量的数量积大于、等于、小于0问题” ?x1x2?y1y2>0;
③“等角、角平分、角互补问题” ?斜率关系(K1?K2?0或K1?K2); ④“共线问题”
????????(如:AQ??QB ?数的角度:坐标表示法;形的角度:距离转化法);
(如:A、O、B三点共线?直线OA与OB斜率相等);
⑤“点、线对称问题” ?坐标与斜率关系;
⑥“弦长、面积问题”
?转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);
六、化简与计算;
七、细节问题不忽略;
①判别式是否已经考虑;②抛物线问题中二次项系数是否会出现0.
基本解题思想:
1、“常规求值”问题:需要找等式,“求范围”问题需要找不等式;
2、“是否存在”问题:当作存在去求,若不存在则计算时自然会无解;
3、证明定值问题的方法:⑴常把变动的元素用参数表示出来,然后证明计算结果与参数无
关;⑵也可先在特殊条件下求出定值,再给出一般的证明。
4、处理定点问题的方法:⑴常把方程中参数的同次项集在一起,并令各项的系数为零,求出定点;⑵也可先取参数的特殊值探求定点,然后给出证明
5、求最值问题时:将对象表示为变量的函数,几何法、配方法(转化为二次函数的最值)、三角代换法(转化为三角函数的最值)、利用切线的方法、利用均值不等式的方法等再解决;
6、转化思想:有些题思路易成,但难以实施。这就要优化方法,才能使计算具有可行性,关键是积累“转化”的经验;
7、思路问题:大多数问题只要忠实、准确地将题目每个条件和要求表达出来,即可自然而然产生思路。
典型例题:
例1、已知点F?0,1?,直线l:y??1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且QP?QF?FP?FQ.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D?0,2?,圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设DA?l1,DB?l2,求
例2、如图半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为
线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上
运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
????????????????l1l2?的最大值. l2l1
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设
求λ的取值范围.
DM=λ,DN
x2y2
例3、设F1、F2分别是椭圆C:2?2?1(a?b?0)的左右焦点。 ab
(1)设椭圆C
上点到两点F1、F2距离和等于4,写出椭圆C的方程和焦点坐标;(2)设K是(1)中所得椭圆上的动点,求线段KF1的中点B的轨迹方程;
(3)设点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线
PM ,PN 的斜率都存在,并记为kPM,kPN ,试探究kPM?KPN的值是否与点P及直线L有关,并证明你的结论。
例4、已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y?kx?m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
例5、已知椭圆两焦点F1、F2在y
轴上,短轴长为
,P是椭圆在第一 2
?????????象限弧上一点,且PF1?PF2?1,过P作关于直线F1P对称的两条直线PA、PB分别交椭圆
于A、B两点。
(1)求P点坐标;
(2)求证直线AB的斜率为定值;
第二篇:高中数学圆锥曲线解题技巧方法总结20xx.01
圆 锥 曲 线 知 识 点 总 结
1.圆锥曲线的两定义:
第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F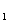 ,F
,F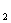 的距离的和等于常数
的距离的和等于常数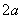 ,且此常数
,且此常数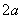 一定要大于
一定要大于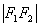 ,当常数等于
,当常数等于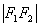 时,轨迹是线段F
时,轨迹是线段F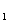 F
F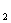 ,当常数小于
,当常数小于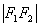 时,无轨迹;双曲线中,与两定点F
时,无轨迹;双曲线中,与两定点F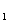 ,F
,F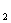 的距离的差的绝对值等于常数
的距离的差的绝对值等于常数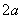 ,且此常数
,且此常数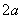 一定要小于|F
一定要小于|F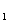 F
F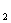 |,定义中的“绝对值”与
|,定义中的“绝对值”与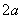 <|F
<|F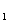 F
F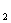 |不可忽视.若
|不可忽视.若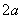 =|F
=|F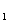 F
F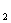 |,则轨迹是以F
|,则轨迹是以F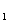 ,F
,F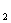 为端点的两条射线,若
为端点的两条射线,若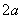 ﹥|F
﹥|F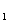 F
F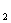 |,则轨迹不存在.若去掉定义中的绝对值则轨迹仅表示双曲线的一支.
|,则轨迹不存在.若去掉定义中的绝对值则轨迹仅表示双曲线的一支.
如方程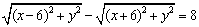 表示的曲线是_____(答:双曲线的左支)
表示的曲线是_____(答:双曲线的左支)
2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):(1)椭圆:焦点在 轴上时
轴上时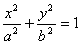 (
(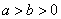 ),焦点在
),焦点在 轴上时
轴上时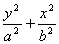 =1(
=1(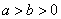 ).方程
).方程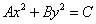 表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B).
表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B).
若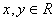 ,且
,且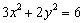 ,则
,则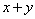 的最大值是____,
的最大值是____,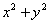 的最小值是___(答:
的最小值是___(答: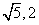 )
)
(2)双曲线:焦点在 轴上:
轴上: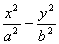 =1,焦点在
=1,焦点在 轴上:
轴上: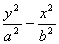 =1(
=1(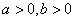 ).方程
).方程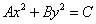 表示双曲线的充要条件是什么?(ABC≠0,且A,B异号).
表示双曲线的充要条件是什么?(ABC≠0,且A,B异号).
如设中心在坐标原点 ,焦点
,焦点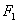 、
、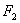 在坐标轴上,离心率
在坐标轴上,离心率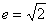 的双曲线C过点
的双曲线C过点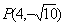 ,则C的方程为_______(答:
,则C的方程为_______(答: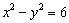 )
)
(3)抛物线:开口向右时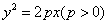 ,开口向左时
,开口向左时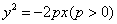 ,开口向上时
,开口向上时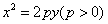 ,开口向下时
,开口向下时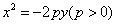 .
.
3.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):
(1)椭圆:由
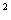 ,
,
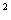 分母的大小决定,焦点在分母大的坐标轴上.如已知方程
分母的大小决定,焦点在分母大的坐标轴上.如已知方程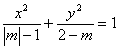 表示焦点在y轴上的椭圆,则m的取值范围是__(答:
表示焦点在y轴上的椭圆,则m的取值范围是__(答: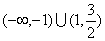 )
)
(2)双曲线:由
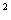 ,
,
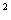 项系数的正负决定,焦点在系数为正的坐标轴上;
项系数的正负决定,焦点在系数为正的坐标轴上;
(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向.
提醒:在椭圆中,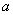 最大,
最大, ,在双曲线中,
,在双曲线中,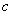 最大,
最大,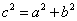 .
.
4.圆锥曲线的几何性质:
(1)椭圆(以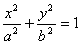 (
(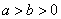 )为例):①范围:
)为例):①范围: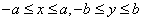 ;②焦点:两个焦点
;②焦点:两个焦点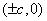 ;③对称性:两条对称轴
;③对称性:两条对称轴 ,一个对称中心(0,0),四个顶点
,一个对称中心(0,0),四个顶点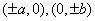 ,其中长轴长为2
,其中长轴长为2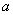 ,短轴长为2
,短轴长为2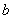 ;④准线:两条准线
;④准线:两条准线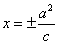 ; ⑤离心率:
; ⑤离心率: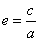 ,椭圆
,椭圆
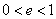 ,
,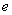 越小,椭圆越圆;
越小,椭圆越圆;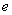 越大,椭圆越扁.
越大,椭圆越扁.
如(1)若椭圆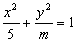 的离心率
的离心率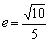 ,则
,则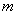 的值是__(答:3或
的值是__(答:3或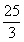 );
);
(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答: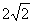 )
)
(2)双曲线(以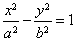 (
(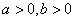 )为例):①范围:
)为例):①范围: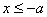 或
或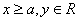 ;②焦点:两个焦点
;②焦点:两个焦点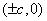 ;③对称性:两条对称轴
;③对称性:两条对称轴 ,一个对称中心(0,0),两个顶点
,一个对称中心(0,0),两个顶点 ,其中实轴长为2
,其中实轴长为2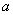 ,虚轴长为2
,虚轴长为2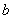 ,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为
,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为 ;④准线:两条准线
;④准线:两条准线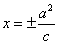 ; ⑤离心率:
; ⑤离心率: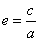 ,双曲线
,双曲线
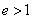 ,等轴双曲线
,等轴双曲线
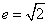 ,
,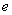 越小,开口越小,
越小,开口越小,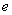 越大,开口越大;⑥两条渐近线:
越大,开口越大;⑥两条渐近线: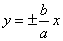 .
.
(3)抛物线(以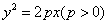 为例):①范围:
为例):①范围: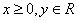 ;②焦点:一个焦点
;②焦点:一个焦点 ,其中
,其中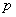 的几何意义是:焦点到准线的距离;③对称性:一条对称轴
的几何意义是:焦点到准线的距离;③对称性:一条对称轴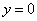 ,没有对称中心,只有一个顶点(0,0);④准线:一条准线
,没有对称中心,只有一个顶点(0,0);④准线:一条准线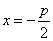 ; ⑤离心率:
; ⑤离心率: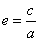 ,抛物线
,抛物线
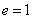 .
.
如设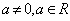 ,则抛物线
,则抛物线 的焦点坐标为________(答:
的焦点坐标为________(答: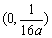 );
);
5.点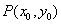 和椭圆
和椭圆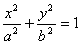 (
(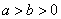 )的关系:
)的关系:
(1)点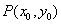 在椭圆外
在椭圆外
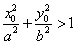 ;(2)点
;(2)点 在椭圆上
在椭圆上
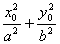 =1;
=1;
(3)点 在椭圆内
在椭圆内
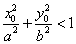
6.直线与圆锥曲线的位置关系:
(1)相交: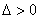
 直线与椭圆相交;
直线与椭圆相交; 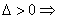 直线与双曲线相交,但直线与双曲线相交不一定有
直线与双曲线相交,但直线与双曲线相交不一定有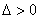 ,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故
,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故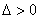 是直线与双曲线相交的充分条件,但不是必要条件;
是直线与双曲线相交的充分条件,但不是必要条件;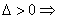 直线与抛物线相交,但直线与抛物线相交不一定有
直线与抛物线相交,但直线与抛物线相交不一定有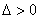 ,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故
,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故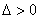 也仅是直线与抛物线相交的充分条件,但不是必要条件.
也仅是直线与抛物线相交的充分条件,但不是必要条件.
(2)相切:
 直线与椭圆相切;
直线与椭圆相切;
 直线与双曲线相切;
直线与双曲线相切;
 直线与抛物线相切;
直线与抛物线相切;
(3)相离: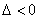
 直线与椭圆相离;
直线与椭圆相离;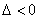
 直线与双曲线相离;
直线与双曲线相离;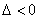
 直线与抛物线相离.
直线与抛物线相离.
提醒:(1)直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交.如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;(2)过双曲线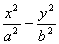 =1外一点
=1外一点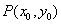 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线.
的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线.
7.焦点三角形(椭圆或双曲线上的一点与两焦点所构成的三角形)
问题: 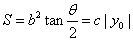 ,当
,当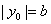 即
即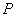 为短轴端点时,
为短轴端点时,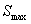 的最大值为bc;对于双曲线
的最大值为bc;对于双曲线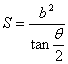 . 练习:点P是双曲线上
. 练习:点P是双曲线上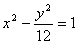 上一点,
上一点,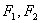 为双曲线的两个焦点,且
为双曲线的两个焦点,且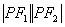 =24,求
=24,求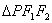 的周长.
的周长.
8.抛物线中与焦点弦有关的一些几何图形的性质:(1)以过焦点的弦为直径的圆和准线相切;(2)设AB为焦点弦, M为准线与x轴的交点,则∠AMF=∠BMF;(3)设AB为焦点弦,A、B在准线上的射影分别为A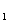 ,B
,B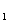 ,若P为A
,若P为A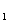 B
B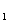 的中点,则PA⊥PB;(4)若AO的延长线交准线于C,则BC平行于x轴,反之,若过B点平行于x轴的直线交准线于C点,则A,O,C三点共线.
的中点,则PA⊥PB;(4)若AO的延长线交准线于C,则BC平行于x轴,反之,若过B点平行于x轴的直线交准线于C点,则A,O,C三点共线.
9、弦长公式:若直线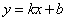 与圆锥曲线相交于两点A、B,且
与圆锥曲线相交于两点A、B,且 分别为A、B的横坐标,则
分别为A、B的横坐标,则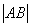 =
=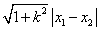 ,若
,若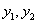 分别为A、B的纵坐标,则
分别为A、B的纵坐标,则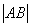 =
=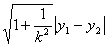 ,若弦AB所在直线方程设为
,若弦AB所在直线方程设为 ,则
,则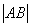 =
=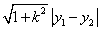 .特别地,焦点弦(过焦点的弦):焦点弦的弦长的计算,一般不用弦长公式计算,而是将焦点弦转化为两条焦半径之和后,利用第二定义求解.
.特别地,焦点弦(过焦点的弦):焦点弦的弦长的计算,一般不用弦长公式计算,而是将焦点弦转化为两条焦半径之和后,利用第二定义求解.
10.圆锥曲线的中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解.
在椭圆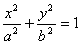 中,以
中,以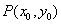 为中点的弦所在直线的斜率k=-
为中点的弦所在直线的斜率k=-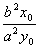 ;
;
弦所在直线的方程: 垂直平分线的方程:
在双曲线 中,以
中,以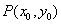 为中点的弦所在直线的斜率k=
为中点的弦所在直线的斜率k=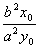 ;在抛物线
;在抛物线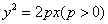 中,以
中,以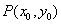 为中点的弦所在直线的斜率k=
为中点的弦所在直线的斜率k=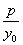 .
.
提醒:因为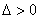 是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验
是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验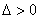 !
!
11.了解下列结论(1)双曲线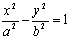 的渐近线方程为
的渐近线方程为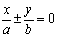 ;
;
(2)以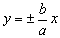 为渐近线(即与双曲线
为渐近线(即与双曲线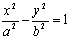 共渐近线)的双曲线方程为
共渐近线)的双曲线方程为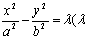 为参数,
为参数,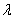 ≠0).
≠0).
(3)中心在原点,坐标轴为对称轴的椭圆、双曲线方程可设为 ;
;
(4)椭圆、双曲线的通径(过焦点且垂直于对称轴的弦)为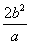 ,焦准距(焦点到相应准线的距离)为
,焦准距(焦点到相应准线的距离)为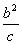 ,抛物线的通径为
,抛物线的通径为 ,焦准距为
,焦准距为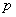 ;
;
(5)通径是所有焦点弦(过焦点的弦)中最短的弦;
(6)若抛物线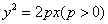 的焦点弦为AB,
的焦点弦为AB, ,则①
,则① ;②
;②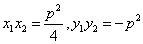
(7)若OA、OB是过抛物线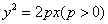 顶点O的两条互相垂直的弦,则直线AB恒经过定点
顶点O的两条互相垂直的弦,则直线AB恒经过定点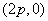
12.圆锥曲线中线段的最值问题:
例(1)抛物线C:y2=4x上一点P到点A(3,4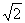 )与到准线的距离和最小,则点 P的坐标为______________
)与到准线的距离和最小,则点 P的坐标为______________
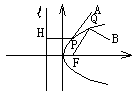 (2)抛物线C: y2=4x上一点Q到点B(4,1)与到焦点F的距离和最小,则点Q的坐标为 .
(2)抛物线C: y2=4x上一点Q到点B(4,1)与到焦点F的距离和最小,则点Q的坐标为 .
分析:(1)A在抛物线外,如图,连PF,则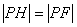 ,因而易发现,当A、P、F三点共线时,距离和最小.
,因而易发现,当A、P、F三点共线时,距离和最小.
(2)B在抛物线内,如图,作QR⊥l交于R,则当B、Q、R三点共线时,距离和最小. 解:(1)(2,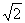 )(2)(
)(2)(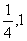 )
)
