一.填空题
1.直线L1 :x?1
1?y?5
?2?z?8
1与L1:??x?y?6
?2y?z?3的夹角?? . 3?
??2.已知设a?2,b?????2,且a?b?2,则a?b? 2 .
?x?y?2z?13. 曲线?在XOY平面上的投影曲线方程为 。 22?y?x?z
?x2?y2?z2?1004. 圆?的,半径为 ,圆心为 。 ?x?2y?2z?18?0
5.曲面z?x2?2y2的名称它与曲面z?6?2x2?y2的交线在xoy面上的投影曲线方程为22??x?y?2, ???z?0.
二.单项选择题
???1.设a, b, c均为非零向量,则与a 不垂直的向量是( D )
??????; (C)a?b; (D)a?(a?b)?a。 ??????a?b?????(A)(a?c)b?(a?b)c; (B)b?aa?a
2.点(1,1,1)到平面2x?y?2z?5?0的距离d?( A )
(A)10
3; (B)3
3.直线L :10x?3y?4z???2?73; (C)3; (D)10。 与平面4x?2y?2z?4?0的关系为( B )
(A)平行,但直线不在平面上; (B)直线在平面上;
(C)垂直相交; (D)相交但不垂直。 1
?x?3y?2z?1?04.已知直线 L:?,平面?:4x?2y?z?2?0则 ( ) 2x?y?10z?3?0?
(A)L平行于?; (B)L在?上 ; (C)L垂直于?; (D)L与?斜交。
5.设平面 ?:2x?7y?4z?1?0及直线L1:x?3t, y?t?1, z?2t?3,
:L2 x?1
?1?y?1
2?z?3
?3,则( C )
(A)?∥L1; (B)??L1; (C)?∥L2; (D)??L2。
6.曲线x
a22
2
2?yb222?1,z?0绕x 轴旋转而成222的曲面方程为( A ) yb22(A)xa?
2y?zb22
2(B)?1;xax?za222?2?1; (C)z?x
a2?y
b;(D)z??yb2?1。
???7.设a?{?1, 2, ?1},b?{1, ?1, 2},c?{3, ?4, 5},则( D )
?????????(A)a?b; (B)b?c; (C)c?a; (D)a, b, c 共面。
8.两非零向量a 及 b的方向角分别为?????, ?, ? 及??, ??, ??,则cos(a, b)?( B )
(A)cos?cos?cos??cos??cos??cos??; (B)cos?cos???cos?cos???cos?cos??;
(C)cos(????)?cos(????)?cos(????);(D)cos(????)?cos(????)?cos(????)。
三.解答题
1.已知两直线L1:x?3
1?y?1
2?z?1
?和L2:x?1?y?1?z相交,求?的值。
?解:L1, L2 的方向向量分别为a1?{1, 2, ?}, a2?{1, 1, 1},
2 ?
A(1, ?1, 1)?L1,B(?1, 1, 0)?L2,AB?{?2, 2, ?1}
1
L1与L2相交?L1与L2共面?[a1 a2 AB]?0?1
?2
?2x?3y?9z?5?0?
x?y?z?1?0
212?
5
1?4??5?0???.
4
?1
2.求过直线?
且垂直于平面2x?y?z?1?0的平面方程。
3.求点P(3,?1,2)到直线L:x?1, y?3t?2, z?3t?4的距离 d。 解法1:直线L的方向向量a?{0, 3, 3},A(1, 2, 4)?L,PA?{?2, 3, 2},
?
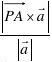
932?
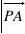
? PA?a?{3, 6, ?6}a?9,d?。
232
?
解法2:过点P 垂直于直线L的平面方程为 0?(x?3)?0?(y?1)?3?(z?2)?0,
即y?z?1?0,把直线L的方程代入平面方程得
1322
:3t?2?3t?4?1?0,t??
1
1
56
。
∴平面与直线L的交点为B(1, ?, ),PB
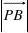
?{?2, , ?,d?2
2
322
。
2x?3y?5?0
三.求过点M(2,1,3)且与直线L:?垂直相交的直线方程。 ?
?x?3z?1?0
?
i
的方向向量为 a ?2
1
?j?30
?k
0?{?9, ?6, 3}??3 {3, 2, ?1}, 3
解:直线L
设所求直线与直线L的交点为A(x?, y?, z?), 则所求直线的方向向量为MA?{x??2, y??1, z??3},
3
?2x??3y??5?0, ?解方程组?x??3z??1?0, ?
??3(x??2)?2(y??1)?( z??3)?0.交点A(, 72137, ?3
7),
2133126246MA?{?2, ?1, ??3}?{?, , ???2, ?1, 4}.7777777
x?2y?1z?3∴所求直线的方程为。 ??2?14 四.已知直线L 过点P(3, 1, ?2),且与两直线L1:x?6?y?4?z?2及L2:x?4
5?y?3
2?z
1
都相交,求L的方程。
解法1:M1(6, ?4, ?2)?L1,PM1?{3, ?5, 0},L1的方向向量a1?{1, 1, 1},
PM1?a1?{3, ?5, 0}?{1, 1, 1}?{?5, ?3, 8},
∴由点P与L1所确定的平面为?1:?5(x?3)?3(y?1)?8(z?2)?0,即5x?3y?8z?34?0。
L2的参数方程为 x?5t?4, y?2t?3, z?t,代入平面?1,得t?1, L2 与 ?1 的交点为M(9,?1,1)
L 的x?3y?1z?2??6?23,。 PM?{6, ?2, 3},∴
解法2:M2(4, ?3, 0)?L2,PMPM2?a2?{?8, 9, 22}, 2?{1, ?4, 2},L2的方向向量a2?{5, 2, 1},
由点P与L2所确定的平面为?2:?8(x?3)?9(y?1)?22(z?2)?0,即8x?9y?22z?59?0。
?5x?3y?8z?34?0
??8x?9y?22z?59?0故交线L 的方程为。
4
解法3:设L 的方程为
lx?3l?y?1m?z?2n,则L 的方向向量a?{l, m, n}, m
1?5m2?4n1?5l?3m?8n?0, 0n1?8l?9m?22n?0, ∴l?2n,m??2
y?1?23nz?2n23n∵[a a1 PM1]?13l[a a2 PM2]?51 ∴L 的方程为x?32n??,即x?3
6?y?1
?2?z?2
3。
5
第二篇:高中解析几何知识点汇总
直线与圆
1.直线方程:⑴点斜式: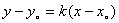
⑵斜截式: ;
;
⑶截距式: ;
;
⑷两点式:
⑸一般式: ,(A,B不全为0)。
,(A,B不全为0)。
2.几个公式:
⑴设A(x1,y1)、B(x2,y2)、C(x3,y3)
⊿ABC的重心G:( );
);
⑵点P(x0,y0)到直线Ax+By+C=0的距离:
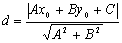 ;
;
⑶两条平行线Ax+By+C1=0与 Ax+By+C2=0
的距离是 ;
;
3.圆的方程:
⑴标准方程:①
②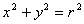 。
。
⑵一般方程: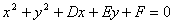 (
(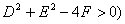
注:Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆 A=C≠0且B=0且D2+E2-4AF>0;
A=C≠0且B=0且D2+E2-4AF>0;
7.圆的方程的求法:⑴待定系数法;
⑵几何法;
⑶圆系法。
8.圆系:⑴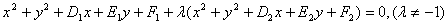 ;
;
注:当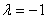 时表示两圆交线。
时表示两圆交线。
⑵ 。
。
9.点、直线与圆的位置关系:(主要掌握几何法)
⑴点与圆的位置关系:( 表示点到圆心的距离)
表示点到圆心的距离)
① 点在圆上;
点在圆上;
②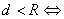 点在圆内;
点在圆内;
③ 点在圆外。
点在圆外。
⑵直线与圆的位置关系:( 表示圆心到直线的距离)
表示圆心到直线的距离)
① 相切;
相切;
②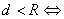 相交;
相交;
③ 相离。
相离。
⑶圆与圆的位置关系:( 表示圆心距,
表示圆心距, 表示两圆半径,且
表示两圆半径,且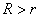 )
)
①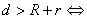 相离;
相离;
②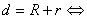 外切;
外切;
③ 相交;
相交;
④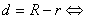 内切;
内切;
⑤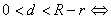 内含。
内含。
10.与圆有关的结论:
⑴过圆x2+y2=r2上的点M(x0,y0)的切线方程为:x0x+y0y=r2;
过圆(x-a)2+(y-b)2=r2上的点M(x0,y0)的切线方程为:(x0-a)(x-a)+(y0-b)(y-b)=r2;
⑵以A(x1,y2)、B(x2,y2)为直径的圆的方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0。
圆锥曲线
1.定义:⑴椭圆: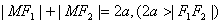 ;
;
⑵双曲线: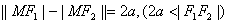 ;⑶抛物线:略
;⑶抛物线:略
2.结论:
1.弦长公式:
 ;
;
注:(Ⅰ)焦点弦长:抛物线: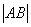 =x1+x2+p;
=x1+x2+p;
(Ⅱ)通径(最短弦):
①椭圆、双曲线: ;②抛物线:2p。
;②抛物线:2p。
2.过两点的椭圆、双曲线标准方程可设为:
( 同时大于0时表示椭圆,
同时大于0时表示椭圆,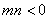 时表示双曲线);
时表示双曲线);
3.椭圆中的结论:①内接矩形最大面积 :2ab;
②P,Q为椭圆上任意两点,且OP 0Q,则
0Q,则 ;
;
③椭圆焦点三角形:<Ⅰ>.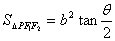 ,(
,( );
);
<Ⅱ>.点 是
是 内心,
内心, 交
交 于点
于点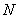 ,则
,则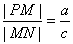 ;
;
④当点 与椭圆短轴顶点重合时
与椭圆短轴顶点重合时 最大;
最大;
4.双曲线中的结论:
①双曲线 (a>0,b>0)的渐近线:
(a>0,b>0)的渐近线: ;
;
②共渐进线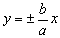 的双曲线标准方程为
的双曲线标准方程为 为参数,
为参数,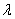 ≠0);
≠0);
③双曲线焦点三角形:<Ⅰ>. ,(
,( );
);
④双曲线为等轴双曲线
 渐近线为
渐近线为
 渐近线互相垂直;
渐近线互相垂直;
5.抛物线中的结论:
①抛物线y2=2px(p>0)的焦点弦AB性质:
<Ⅰ>. x1x2=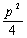 ;y1y2=-p2;
;y1y2=-p2;
<Ⅱ>. ;
;
<Ⅲ>.以AB为直径的圆与准线相切;
<Ⅳ>.以AF(或BF)为直径的圆与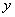 轴相切;
轴相切;
<Ⅴ>.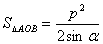 。
。
。
