概率论第二章随机变量的分布总结
第二篇:概率论课件:第二章随机变量及其概率分布
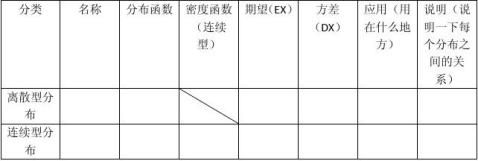
第二章 随机变量及其概率分布
(一)基本题
27.假设随机变量X~N(0,1),求下列随机变量Y的概率密度函数:
(1)Y=eX;(2)Y=2X2+1;(3)Y=X.
26.假设随机变量X具有连续的分布函数F(x):Y=F(X)在区间(0,1)上服从均匀分布.
?e?x,x≥0,25.设随机变量X的概率密度为fX(x)=?求随机变量Y=ex的概率密度fY(y).
?0,x<0,
24.随机变量X服从(0,2)上的均匀分布,试求随机变量Y=X2的概率密度fY(y).
?123.设随机变量X的分布律为?1??22?n11?42n???,Y=sinπX,求Y的分布律。 ??2?
π3π??π0??22.设随机变量X的分布律为?22?,求Y的分布律:
?0.30.20.40.1?
(1)Y=(2X?π); (2)Y=cos(2X?π).
?2x,0<x<121.设随机变量X的概率密度 f(x)=? 0,其它?22、解 2
Y=2}. 以Y表示对X的三次独立重复观察中事件{X≤1/2}出现的次数,求p{
20.在电源电压不超过200V、在200~240V和超过240V三种情形下,某种电子元件损坏的概率分别为0.1、0.001和0.2,假设电源电压X服从正态分布N(220,252),试求:(1)该电子元件损坏的概率α;(2)该电子元件损坏时,是电源电压在200V~240V的概率β.
19.某种电池的寿命X服从正态分布N(μ,σ2),其中μ=300h, σ=35h. (1)求电池寿命在250h以上的概率;(2)求x,使寿命在μ?x与 μ+x之间的概率不小于0.9.
18.某地抽样调查结果表明,考生的外语成绩(百分制)近似服从正态分布N(72,σ2),96分以上的占考生总数的2.3%,试求考生的外语成绩在60分至84分之间的概率.
[附表] x 0 0.5 1.0 1.5 2.0 2.5 3.0
0.500 0.692
表中Φ(x)是标准正态分布函数. Φ(x)0.8410.9330.9770.9940.999
17.设某地长为t的时间内发生地震的次数N(t)服从参数为λt的泊松分布,设T表示相邻两次地震之间的时间间隔.(1)求T的分布函数;(2)求连续5年未发生地震的情形下,在未来5年内仍不会发生地震的概率Q.
16.考虑一元二次方程x2+Bx+C=0,其中B,C分别是将一枚骰子接连掷两次先后出现的点数,求该方程有实根的概率p和有重根的概率q.
1
15.某型号的飞机雷达发射管的寿命X(单位:h)服从参数为1的指数分布,求下列事200
件的概率,(1)发射管的寿命不超过100h;(2)发射管的寿命超过300h.
14.设某地区每天的用电量X(单位:100万KW)是一连续型随机变量,其概率密度
?12x(1?x)2,0<x<1f(x)=? 其他?0,
假设该地区每天的供电量仅有80万KW,求该地区每天供电量不足的概率.若每天的供电量上升到90万KW,每天供电量不足的概率又是多少?
?1/3,x∈[0,1]?13.设随机变量X的概率密度为 f(x)=?2/9,x∈[3,6] 若k使得P{X≥k}=2/3,试求
?0,其它.?
k的取值范围.
12.已知随机变量X的概率密度函数f(x)=
11.设连续型随机变量X的分布函数为 1?xe,?∞<x<+∞,试求X的分布函数. 2
?a+bexp(?x2/2),x≥0F(x)=? x<0,?0,
(1)求常数a和b; (2)求随机变量X的概率密度函数.
10.设随机变量X的分布函数
x<?1?0,?0.4,?1≤x<1?F(x)=P{X≤x}=? ≤<0.8,13x??x≥3,?1,
试求X的分布律.
9.一台设备由三大部件构成,在设备运行中各部件需要调整的概率相应为0.10,0.20和0.30,假设各部件的状态相互独立,以X表示同时需要调整的部件数,求X的概率分布.
8.为保证设备的正常运行,必须配备一定数量的设备维修人员.现有同类设备180台,且各台工作相互独立,任意时刻发生故障的概率都是0.01,假设一台设备的故障需一人进行修理,问至少应配备多少名修理工人,才能保证设备发生故障后能得到及时维修的概率不小于0.99?
7.一个完全不懂中文的外国人去瞎懵一个中文考试,假设此考试有5个选择题,每题有4种选择,其中只有一种答案是正确的.试求:他居然能答对三题以上而及格的概率.
6.设某商店中每月销售某种商品的数量服从参数为5的泊松分布,问在月初进货时要库存此种商品多少,才能保证当月不脱销的概率为0.999.
5.设一个试验只有两种结果:成功或失败,且每次试验成功的概率为p(0<p<1),现反复试验,直到获得k次成功为止.以X表示试验停止时一共进行的试验次数,求X的分布律.
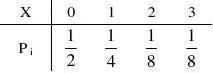
4.设离散型随机变量X的分布律为P{X=k}=c/15,k=1,2,3,4,5..
(1)试确定常数C; (2)求P{1≤X≤3}; (3)P{0.5<X<2.5}.
不放回地连续从袋中取球,直到取出黑球为止.3.一个口袋中装有m个白球,n?m个黑球,
设此时已经取出了X个白球,试求X的分布律.
2
2.一汽车沿一街道行驶,需要通过三个均设有红绿信号灯的路口,每个信号灯为红或绿与其他信号灯为红或绿相互独立,且红绿两种信号显示的时间相等,以X表示该汽车首次遇到红灯前已通过的路口的个数,求X的分布律.
1.掷一颗匀称的骰子两次,以X表示前后两次出现的点数之和,求X的分布律.
(二)解答 1、解 样本空间V={(1,1),(1,2),?,(1,6),(2,1),(2,2),?,(2,6),?,(6,1),?,(6,6)}.这里,例如(6,1)表示掷第一次得6点,掷第二次得1点.其余类推.
以X
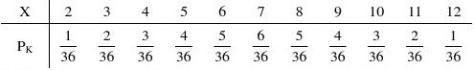
2、分析: 显然X服从离散型概率分布,而且X的可能取值为0,1,2,3.问题归结为求概率P{X=k},k=0,1,2,3.
解:由题设,X的可能值为0,1,2,3. 以Ai(i=1,2,3)表示事件“汽车在第i个路口 遇到红灯”;A1,A2,A3相互独立,且P(Ai)=P(i)=1/2,i=1,2,3.于是
P{X=3}=P(123)=1/23.
∴ X的分布律为:
P{X=0}=P(A1)=1/2;P{X=1}=P
(1A2)=1/22;P{X=2}=P(12A3)=1/23;
3、解 设“ξ=k”表示前次取出白球,第次取黑球,则ξ的分布列为
m(m?1)?(m?k+1)(n?m)
P(ξ=k)=(k=0,1,?,m).
n(n?1)?(n?k)cc5cc
4、解 (1)∵P(X=k)===×5==1,
1515k=1153k=1k=1
∑
5
∑
5
∑
∴c=3.
13
1≤X≤3}== (3)P{0.5<X<2.5}=(2)P{
55k=1
∑
3
∑5=5
k=1
2
12
5、解 设进行了i次试验,其中有k次试验成功之事件设为A,则此事件包含有两层意思:它意味着第i次(i≥k)成功,且i?1次试验中成功k?1次,设这两个事件分别为A1,A2, 则A=A1A2,且P(A)=P(A1A2)=P(A1)P(A2)(A1与A2独立),而P(A1)=p,
1k?11k?1i?k
P(A2)=Cik???qi?1?(k?1)=Cik??q. 1p1?p
于是,所需试验次数X的分布律为
1k?1i?k1ki?kP{X=i}=p?cik??q=cik??(i=k,k+1,?;q=1?p). 1p1pq
6、解:设ξ为该种商品每月销售数,则 ξ~π(7), x为该种商品每月进货数,则P(ξ≤x)≥0.999.查普哇松分布的数值表,得x≥13.
7、解 设X={该外国人在5个选择题中答对的题数},则X~B(5,1/4).又设A={答对题数不少于两题},则依题设知 P(A)=
∑
k=3
5
P{X=k}=
∑
k1k35?k
C5()(=0.1035.
44k=3
5
8、解 设X={180台同类设备中同时发生故障的设备的台数},则X~B(180,0.01).又
3
设配备N个维修人员,则所求概率为
P{X>N}=P{X≥N+1}=
180k=N+1∑P{X=k}k180?k180k,而P{X=k}=C180(0.01)k(0.99)180?k,故P{X>N}=
k=N+1∑c(0.01)(0.99)k180(1.8)k?1.8≈∑ek!k=N+1∞,这里
np=180×0.01=1.8=λ. 1.8k?1.8e≤1?0.99=0.01,查泊松分布表,可知N+1=7,因而至少应配备6名工人. 欲使k!k=N+1∑∞
,则P(A1)=0.10,P(A2)=0.20, 9、解 设Ai={部件i需要调整}(i=1,2,3)
P(A3)=0.30. 由于A1,A2,A3相互独立,因此,有
P{X=0}=P(123)=P(1)P(2)P(3)=(1?0.1)×(1?0.2)×(1?0.3)=0.504, P{X=1}=P(A123)+P(1A23)+P(12A3)
=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398,
P{X=2}=P(A1A23)+P(A12A3)+P(1A2A3)=0.092,
P{X=3}=P(A1A2A3)=P(A1)P(A2)P(A3)=0.1×0.2×0.3=0.006. 因此,X的概率分布为 0.3980.0920.006
10、解 F(x)为一阶梯状函数,则X可能取得值为F(x)的跳跃点:?1,1,3
P(X=?1)=F(?1)?F(?1?0)=0.4,P(X=1)=F(1)?F(1?0)=0.8?0.4=0.4,P(X=3)=F(3)?F(3?0)=1?0.8=0.2,即有 X ?1
0.2
x→+∞11、解 (1)由于limF(x)=1,所以有lim(a+bexp?x2/2)=a=1,即a=1,又由于Xx→+∞{}
为连续型随机变量,F(x)应为x的连续函数,应有
x→0lim?F(x)=0=lim+F(x)=lim+(a+bexp?x2/2)=a+b 所以a+b=0,b=?a=?1. x→0x→0{}
?1?exp?x2/2,x>0,代入a,b之值,得F(x)=? x0,≤0.?
?xexp?x2/2,x≥0,(2)对函数F(x)求导,得X的概率密度P(x)=? x<0.?0,
12、解 当x≤0, F(x)=
F(x)=1(2{}{}∫01t1edt=ex;当x>0时, ?∞22x∫0?∞etdt+∫xe?tdt)=11[1+(1?e?x)]=1?e?x,所以,我们有 22
?ex/2,x≤0,F(x)=? ?x?1?e/2,x>0.
4
13、解 由P{X≥k}=
21
得P{X<k}=,即应选k,使33
∫
k?∞
f(x)dx=
1
.注意3
∫
?∞
f(x)dx=0,
∫∫
10
1
f(x)dx=,
3f(x)dx=
∫
31
f(x)dx=0,
∫
63
f(x)dx=
2
,可见当1≤k≤3时, 3
1
,所以k的取值范围应为1≤k≤3. 3
k?∞
∫
?∞
f(x)dx+
∫∫
101
f(x)dx+
∫
k1
f(x)dx=
14、解 P{X>0.8}=
0.8
12x(1?x)2dx=0.272. P{X>0.9}=
∫
1
0.9
12x(1?x)2dx=0.037.
1
??1
(1)P(X≤100)=F(100)=1?e200=1?e2; 15、解 X~E(200
?1
300200
?32
100
(2)P(X>300)=e=e
=e?1.5.
16、解1 用随机变量法:令xi表示第i 次掷骰子出现的点数,i=1,2. 显然x1和x2独立同分布,P{xi=j}=1/6,(j=1,2,?,6;i=1,2),则方程变为x2+x1x+x2=0.它有重根的充要条件
22是x1?4x2=0,有实根的充要条件是x1?4x2≥0,故
2
q=Px1?4x2=0=P({x2=1,x1=2}U{x2=4,x1=4})=P{x2=1,x1=2}+P{x2=4,x1=4}
{}
=P{x2=1}P{x1=2}+P{x2=4}P{x1=4}=1/6×1/6+1/6×1/6=1/18. 由全概率公式可
得P=P
{
2
x1
2x1
?4x2≥0=P{x2≤}=
4
}
∑
i=1
6
2x1
x=j} P{x1=j}P={x2≤
41
2232421
}+P{x1=3}P{x2≤}+P{x1=4}P{x2≤}=P{x1=1}P{x2≤}+P{x1=2}P{x2≤4444
526211112141119
}+P{x2≤}=×0+×+×+×+×1+×1= +P{x1=5}P{x2<4466666666636
解2 用枚举法:一枚骰子掷2次,其基本事件总数为36.方程有实根和重根的充要条件分别为B2?4C≥0和B2?4C=0.
B的取值
使B2?4C≥0的基本事件个数 使B2?4C=0的基本事件个数
故使方程有实根的基本事件总数为1+2+4+6+6=19,有重根的基本事件总数1+1=2, 因此 P=19/36,q=2/36=1/18.
解 本题关键是理解随机变量N(t)的意义.事件{N(t)=k}表示设备在任何长为t的时间17、
(λt)k?λt
内发生k次地震,其概率为P{N(t)=k}=e(k=0,1,2,?). 由于T表示两次地震之间的
k!当t≥0时,事件{T≤t}与事件{T>t}是互逆事件,且{T>t}时间间隔,故当t<0时,P{T≤t}=0;表示在长为t的时间内无地震发生,故它等价于事件{N(t)=0}.
5
(1)由于T是非负随机变量,可见当t<0时,F(t)=P{T≤t}=0.
设t≥0,则事件{T>t}与{N(t)=0}等价. 因此,当t≥0时,有
F(t)=P{T≤t}=1?P{T>t}=1?P{N(t)=0}=1?e?λt.
于是,T服从参数为λ的指数分布.
P{T≥10,T≥5}P{T≥10}e?10t
T≥10T≥5}===?5t=e?5t. (2)Q=P{PT≥5PT≥5e
18、解 设X为考生的外语成绩,由题设知X~N(μ,σ),其中μ=72.现在求σ2.由题设
2424?X?μ96?72?≥P{X≥96}=0.023,P?=1?Φ()=0.023,∴Φ(=0.977, ?σσσσ??
由Φ(x)的数值表,可见24
σ=2,因此σ=12.这样X~N(72, 122). 所求概率为
X?μ??P??1≤≤1? σ???60?72X?μ84?72?≤≤P{60≤x≤84}=P??=1212σ??
=Φ(1)?Φ(?1)=2Φ(1)?1=2×0.841?1=0.682.
19、解 (1)p(ξ>250)=p(ξ?300
35>250?300=Φ(1.43)≈0.9236; 35
(2)p(μ?x<ξ<μ+x)=p(?xxxxξ?300x<<=Φ(?Φ(?)=2Φ(?1≥0.9, 353535353535即(x/35)≥0.95,所以x/35≥1.65,即x≥57.75.
,A2={电压在200~240伏},A3={电20、解 引进下列事件:A1={电压不超过200伏}
;B={电子元件损坏}.由题设,知X~N(220,252),因此 压超过240伏}
?X?220200?220?P(A1)=P{X≤200}=P?≤=Φ(?0.8)=0.212; 2525??
P(A2)=P{200≤X≤240}=Φ(0.8)?Φ(?0.8)=0.576;
P(A3)=P{X>240}=1?0.212?0.576=0.212.
3(1)由题设条件,知P(BA1)=0.1,P(B|A2)=0.001,P(B|A3)=0.2. 于是,由全概
率公式,有α=P(B)=∑P(A)P(B|A)=0.0642. ii
i=1
(2)由条件概率定义(或贝叶斯公式),知β=P(A2|B)=
1P(A2)P(B|A2)≈0.009. P(B)11?1?21、解:由题设,Y~B(3,P)其中P=P?X≤=∫2f(x)dx=∫22xdx= 02??∞4?
2故 P{Y=2}=C3(1/4)2(3/4)1=9/64.
6
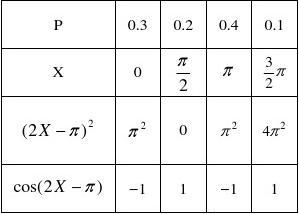
∴
(2X?π)2
π2 4π?2
cos(2X?π)
?1
??1,k=4n?1,
kπ?
23、解 因为 sin=?0,k=2n,
2?1,k=4n?3
?
(n=1,2,?).
所以,Y=sin(
π
2
X)只有3个可能取值?1,0,1,而取这些值的概率分别为
P{Y=?1}=P{X=3}+P{X=7}+P{X=11}+?=P{Y=0}=P{X=2}+P{X=4}+P{X=6}+?=P{Y=1}=P{X=1}+P{X=5}+P{X=9}+?=
??101?
于是,Y=sin(X)的分布列为?218?.
2??15315??
123+
+124
127+
+126
1211=
+?=
112
?= 81?1/1615,
122
111?=,41?1/43
111118+5+9+?=?=.2221?1/16152
π
24、解 ∵X~U(0,2), ∴①y≤0时,FY(y)=0;
②当0<y<4,
FY(y)=P(Y≤y)=P(X2≤y)=P(X≤
y)=FX(y)=
y;
③y≥4时,Fy(y)=1.
?1
,0<y<1?
故 fY(y)=?4y
?0,其它,?
25、解 应先求出FY(y),再对y求导即得fY(y) 因 FY(y)=p{Y<y}=peX<y=?故当y≥1时,FY(y)=p{X<lny}=
?0,
?p{X<Iny},
y<1,y≥1.
{}
∫
lny0
e?xdx, 而fY(y)=FY′(y)=1/y2.
?0,
因此 fY(y)=?2
?y
y<1,y≥1.
26、解 先求Y的分布函数. 因0≤F(x)≤1,单调非降. 连续,故y=F(x)的反函数存在.
7
当y≤0时,FY(y)=P(F(X)≤y)=P(φ)=0,
当0<y<1时FY(y)=P(F(X)≤y)=P(X≤F?1(y))=F[F?1(y)]=y, 当y≥1时FY(y)=P(F(X)≤y)=P(Ω)=1.
?0,y≤0?1,
于是 FY(y)=?y,0<y<1 从而Y的密度函数为 fY(y)=??0,
??1,y≥1,
?
0≤y<1
其他.
即Y= F(X)服从(0,1)上的均匀分布.
27、解 (1)Y=eX 的分布函数 FY(y)=P(Y≤y)=P(eX≤y).当y≤0 时,FY(y)=0;
当y>0时,FY(y)=P{e
X
≤y}=P{X≤lny}=
∫
lny0
x2
exp{?dx, 于是,Y的概
22π1
?0,
?
率密度函数为 fY(y)=?1exp[?1(lny)2],
?y22?
y≤0;y>0.
(2)Y=2X2+1的分布函数FY(y)=P2X2+1≤y.当y≤1时,FY(y)=0;当y>1时,
{}
??
FY(y)=p2X2+1≤y=P??
??
{}
y?1
≤X≤2
y?1?
?=2??
∫
y?1
2y?1?
2
12π
e
?
x22
dx=
2π∫
2
y?120
e
?
x22
dx,
??0,?
即FY(y)=?
?2??2π
∫
y?12
e
?
x22
dx,
y?1??1
e4,?y≤1,
?2(y?1)
故Y的概率密度为fY(y)=?
?0,
y>1.?
?
y>1,y≤1.
. 当y≤0时,FY(y)=0;当y>0时, (3)Y=X的分布函数 FY(y)=P{Y≤y}=PX≤y}
FY(y)=PX≤y}=P{?y≤X≤y}=
∫
y
12?y
e
?
x22
dx=
22∫
y
?y
e
?
x22
dx.
?0,?1
于是,Y的概率密度函数为 fY(y)=FY′(y)=?2?2y2
,?πe
?
y≤0,y>0.
8
