题型1 已知数列前几项求通项公式
1.数列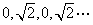 的通项
的通项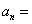
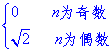 .
.
2.数列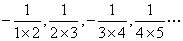 的通项
的通项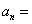
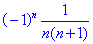 .
.
3.数列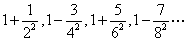 的通项
的通项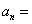
 .
.
4. 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
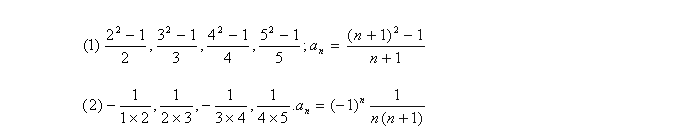
5. 观察下面数列的特点,写出每个数列的一个通项公式:


6.写出下面数列的一个通项公式:
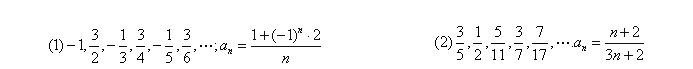
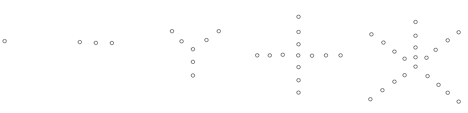 7.根据下列5个图形及相应点的个数的变化规律,猜测第
7.根据下列5个图形及相应点的个数的变化规律,猜测第 个图中有__n2-n+1_个点.
个图中有__n2-n+1_个点.
(1) (2) (3) (4) (5)
相关的高考试题有:
(2004年全国卷)已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项 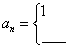
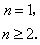

分析:由已知,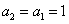 .
.
由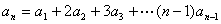 生成
生成
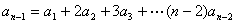
两式相减得: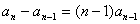 ,即
,即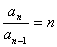
为商型的,用累乘法可得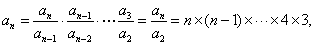
 (20##年广东卷)在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第
(20##年广东卷)在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第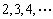 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第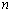 堆第
堆第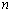 层就放一个乒乓球,以
层就放一个乒乓球,以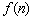 表示第
表示第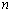 堆的乒乓球总数,则
堆的乒乓球总数,则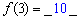 ;
;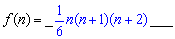
(答案用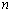 表示).
表示).
题型2 由an与Sn的关系求通项公式
 =
=
 =
=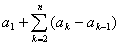 .
.
一般已知条件中含an与Sn的关系的数列题均可考虑用上述公式.
1. 已知数列 的前
的前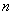 项和
项和 ,则
,则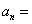 n .
n .
2. 已知数列 的前
的前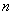 项和
项和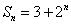 ,则
,则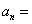
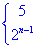
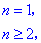 .
.
3:(04年浙江)设数列{an}的前项的和Sn=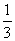 (an-1) (n
(an-1) (n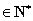 ).
).
(Ⅰ)求a1;a2;
(Ⅱ)求证数列{an}为等比数列.
4. 数列{an}的前n项和 Sn=3·2n-3,求数列的通项公式.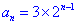
5:设数列{an}的前n项和为Sn=2n2+3n+2,求通项an的表达式,并指出此数列是否为等差数列. 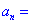
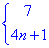
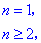
6:已知数列{an}的前n项和为Sn,a1=2,且nan+1=Sn+n(n+1),求an.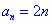
7. (2004全国卷)已知数列{an}的前n项和Sn满足:Sn=2an +(-1)n,n≥1.
(Ⅰ)写出求数列{an}的前3项a1,a2,a3;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)证明:对任意的整数m>4,有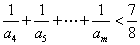 .
.
8..(20##年湖北卷)已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为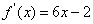 ,数列
,数列 的前n项和为
的前n项和为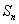 ,点
,点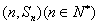 均在函数
均在函数 的图像上.
的图像上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设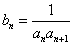 ,
,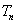 是数列
是数列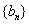 的前n项和,求使得
的前n项和,求使得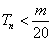 对所有
对所有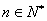 都成立的最小正整数m.
都成立的最小正整数m.
点评:本小题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力.
9. (20##年安徽卷)数列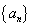 的前
的前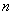 项和为
项和为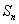 ,已知
,已知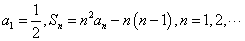 .
.
(Ⅰ)写出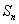 与
与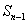 的递推关系式
的递推关系式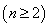 ,并求
,并求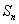 关于
关于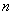 的表达式;
的表达式;
(Ⅱ)设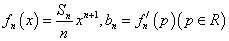 ,求数列
,求数列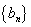 的前
的前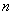 项和
项和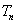 .
.
题型3 已知数列递推公式求通项公式
1. 已知数列 的首项
的首项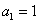 ,且
,且 ,则
,则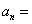 3n-2 .
3n-2 .
2.已知数列 的首项
的首项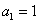 ,且
,且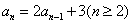 ,则
,则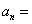
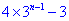 .
.
3.已知数列 的
的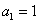 ,
,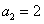 且
且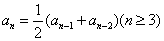 ,则
,则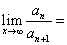 1 .
1 .
4. 已知数列 的
的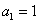 ,
,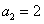 且
且 ,则
,则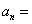 n .
n .
一、由等差,等比演化而来的“差型”,“商型”递推关系

析:①等差数列:
生成: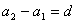 ,
,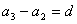 ,…
,…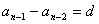 ,
,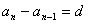
累加: =
=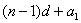
由此推广成差型递推关系: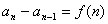
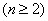
累加: =
=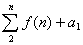 ,于是只要
,于是只要 可以求和就行.
可以求和就行.
题组一:
数列 中,
中,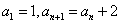 ,求
,求 的通项公式 .
的通项公式 .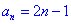
变式1:数列 中,
中,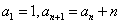 ,求
,求 的通项公式 .
的通项公式 .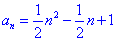
变式2:数列 中,
中,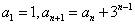 ,求
,求 的通项公式 .
的通项公式 .
变式3:已知数列 满足
满足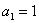 ,
,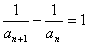 ,求
,求 .
.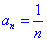
变式4:数列 中,
中, ,求
,求 的通项公式 .
的通项公式 .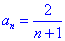

析:②等比数列: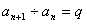
生成: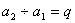 ,
,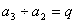 ,…
,…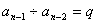 ,
,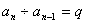
累乘: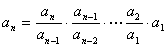 =
=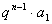
由此推广成商型递推关系: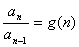
累乘: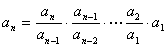
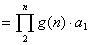
题组二、
已知数列 的首项
的首项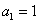 ,且
,且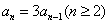 ,则
,则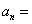
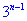 .
.
变式1:已知数列 的首项
的首项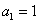 ,且
,且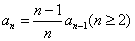 ,则
,则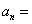
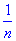 .
.
变式2:数列 中,
中,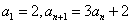 ,求
,求 的通项公式.
的通项公式.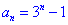
变式3:数列 是首项为1的正项数列,
是首项为1的正项数列,
且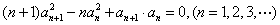 ,求
,求 的通项公式.
的通项公式.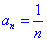
例1、 若数列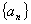 满足:
满足: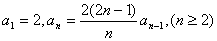 .
.
求证:① ; ②
; ② 是偶数 .
是偶数 .
例2、已知数列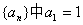 ,且
,且 ,
, 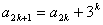 其中k=1,2,3,……. (I)求
其中k=1,2,3,……. (I)求 ;(II)求{ an}的通项公式.
;(II)求{ an}的通项公式.
二.由差型,商型类比出来的和型,积型:
即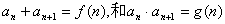
例如:数列 中相邻两项
中相邻两项 ,
,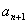 是方程
是方程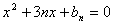 的两根,已知
的两根,已知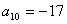 ,求
,求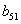 的值.
的值.
分析: 由题意: +
+ ①
①
生成: 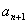 +
+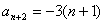 ②
②
②—①: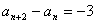 .
.
所以该数列的所有的奇数项成等差,所有的偶数项也成等差.
其基本思路是,生成,相减;与“差型”的生成,相加的思路刚好相呼应.到这里本题的解决就不在话下了.
特别的,若 +
+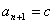 ,则
,则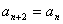 .
.
即该数列的所有的奇数项均相等,所有的偶数项也相等.
若 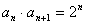 ①
①
则  ②
②
②÷①: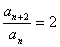 .
.
所以该数列的所有的奇数项成等比,所有的偶数项也成等比.
其基本思路是,生成,相除;与“商型”的生成,相乘的思路刚好相呼应.
特别地,若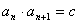 ,则
,则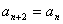 .
.
即该数列的所有的奇数项均相等,所有的偶数项也相等.
三.可以一次变形后转化为差型,商型的
1.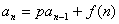
例如:设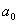 是常数,且
是常数,且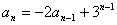 ,(
,(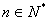 ).
).
证明: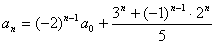 .
.
分析:这道题目是证明型的,最简单的方法当然要数数学归纳法,现在我们考虑用推导的方法来处理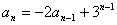 的三种方法:
的三种方法:
方法(1):构造公比为—2的等比数列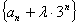 ,用待定系数法可知
,用待定系数法可知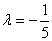 .
.
方法(2):构造差型数列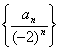 ,即两边同时除以
,即两边同时除以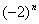 得:
得: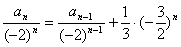 ,从而可以用累加的方法处理.
,从而可以用累加的方法处理.
方法(3):直接用迭代的方法处理:
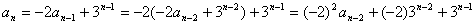
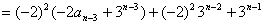
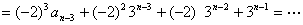
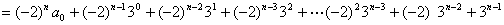
 .
.
说明:①当 时,上述三种方法都可以用;
时,上述三种方法都可以用;
②当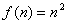 时,若用方法1,构造的等比数列应该是
时,若用方法1,构造的等比数列应该是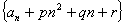 而用其他两种方法做则都比较难.
而用其他两种方法做则都比较难.
③用迭代法关键是找出规律,除含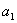 外的其它式子,常常是一个等比数列的求和问题.
外的其它式子,常常是一个等比数列的求和问题.
2.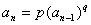 型
型
例如:已知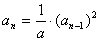 ,首项为
,首项为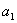 ,求
,求 .(20##年江苏卷22题改编)
.(20##年江苏卷22题改编)
方法1:两端取常用对数,得 ,
,
令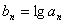 ,则
,则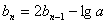 ,转化如上面类型的.
,转化如上面类型的.
特别的,a=1,则转化为一个等比数列.
方法2:直接用迭代法:
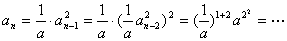
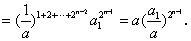
四.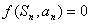 型的
型的
利用 转化为
转化为 型,或
型,或 型
型
即混合型的转化为纯粹型的.
例如: 已知数列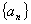 的前n项和Sn满足
的前n项和Sn满足
(Ⅰ)写出数列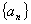 的前3项
的前3项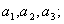
(Ⅱ)求数列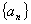 的通项公式.
的通项公式.
分析: -①
-①
由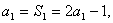 得
得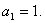 -②
-②
由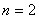 得,
得, ,得
,得 -③
-③
由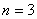 得,
得,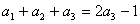 ,得
,得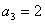 -④
-④
用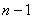 代
代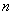 得
得 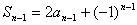 -⑤
-⑤
①—⑤: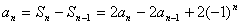
即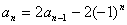 --⑥
--⑥


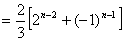 -⑦
-⑦
又如:数列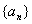 的前n项和记为
的前n项和记为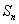 ,已知
,已知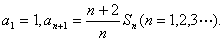
证明:数列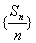 是等比数列
是等比数列
方法1∵
∴ 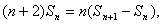 整理得
整理得 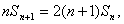
所以 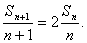 故
故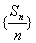 是以2为公比的等比数列.
是以2为公比的等比数列.
方法2:事实上,我们也可以转化为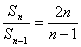 ,为一个商型的递推关系,
,为一个商型的递推关系,
由 =
=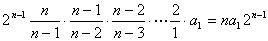 .
.
当然,还有一些转化的方法和技巧,如基本的式的变换,象因式分解,取倒数等还是要求掌握的.

成与迭代是递推关系的最重要特征.递推关系一般说来,是对任意自然数或大于等于2的自然数总成立的一个等式,自然数n可以取1,2,3…n,n+1等等,这样就可以衍生出很多的等式.这就是所谓的生成性.对于生成出来的等式,我们往往选一些有用的进行处理.比如相加,相减,相乘,相除等,但用的最多的还是由后往前一次又一次的代入,直到已知项.这种方法就叫迭代.上面的很多例题都可以体现这一点.这种很朴素的思想,对于相关的其他数列问题也是非常有效的.
例题练习
1、(20##年全国卷)已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项 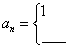
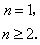
2.已知数列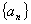 中,
中,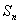 是其前
是其前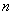 项和,并且
项和,并且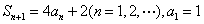 ,
,
(Ⅰ)设数列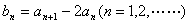 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(Ⅱ)设数列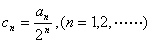 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
(Ⅲ)求数列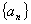 的通项公式及前
的通项公式及前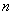 项和.
项和.
3.(04年重庆)设a1=1,a2=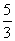 ,an+2=
,an+2=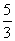 an+1-
an+1-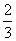 an (n=1,2,---),令bn=an+1-an (n=1,2---).
an (n=1,2,---),令bn=an+1-an (n=1,2---).
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)求数列{nan}的前n项的和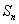 .
.
4.(04年全国)已知数列{an}中,a1=1,a2k=a2k-1+(-1)K,a2k+1=a2k+3k,其中k=1,2,3,….
(I)求a3,a5;
(II)求{an}的通项公式.
5.(20##年全国)已知数列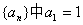 ,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k, 其中k=1,2,3,…….
,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k, 其中k=1,2,3,…….
(I)求a3, a5;
(II)求{ an}的通项公式.
6.(20##年天津理)已知定义在R上的函数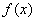 和数列
和数列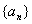 满足下列条件:
满足下列条件:
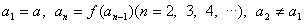 ,
,
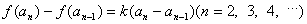 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(I)令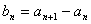
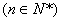 ,证明数列
,证明数列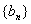 是等比数列;
是等比数列;
(Ⅱ)求数列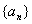 的通项公式;
的通项公式;
(Ⅲ)当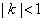 时,求
时,求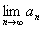 .
.
7.(20##年重庆卷)在数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an=_________.
8.(20##年福建卷)已知数列{a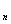 }满足a
}满足a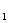 =1,a
=1,a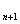 =2a
=2a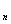 +1(n∈N
+1(n∈N )
)
(Ⅰ)求数列{a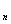 }的通项公式;
}的通项公式;
(Ⅱ)若数列{bn}满足4k1-14k2-1…4k-1=(an+1)km(n∈N*),证明:{bn}是等差数列;
(Ⅲ)证明: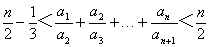 (n∈N*).
(n∈N*).
第二篇:数列题型分类总结
数列(2)
【类型1】
1.已知?an?是一个公差大于0的等差数列,且满足a3?a6?55,, a2?a7?16, (Ⅰ)求数列?an?的通项公式:
b1b2b3bn???...(n为正整数),(Ⅱ)若数列?an?和数列?bn?满足等式:?an?=23n2222
求数列?bn?的前n项和sn
解(1)设等差数列?an?的公差为d,则依题设d?0 由a2?a7?16得2a1?7d?16 ① 由a3?a6?55,得(a1?2d)(a1?5d)?55 ②
2由①得2a1?16?7d将其代入②得(16?3d)(16?3d)?220,即256?9d?220。
?d2?4,又d?0,?d?2,代入①得a1?1?an?1?(n?1)?2?2n?1
(2)令cn?bn,则有an?c1?c2?2n ?cn,an?1?c1?c2??cn?1两式相减得an?1?an?cn?1,由(1)得a1?1,an?1?an?2
?cn?1?2,cn?2(n?2),即当n?2时,bn?2n?1又当n=1时,b1?2a1?2
?2,(n?1)?bn??n?1?2(n?2)
于是Sn?b1?b2?b3
23?bn?2?23?24?4?2n?1 =2?2?2?2??2n?12(2n?1?1)?4?2n?2?6,即Sn?2n?2?6 -4=2?1
2.已知等差数列{an}的公差为d(d?0),等比数列{bn}的公比为q(q?0)。设
?Sn?a1b1+a2b2…..+ anbn,Tn=a1b1-a2b2+…..+(-1)n?1 anbn,n?N
(1) 若a1=b1= 1,d=2,q=3,求 S3 的值;
2dq(1?q2n)
(2) 若b1=1,证明(1-q)S2n-(1+q)T2n=,n?N?; 2
1?q(3) 若正数n满足2?n?q,设k1,k2,...,kn和l1,l2,...,ln是1,2...,,n的两个不同的排列, c1?ak1b1?ak2b2?...?aknbn, c2?al1b1?al2b2?...?alnbn 证明c1?c2。
n?1*(Ⅰ)解:由题设,可得an?2n?1,bn?3,n?N
所以,S3?a1b1?a2b2?a3b3?1?1?3?3?5?9?55
n?1
(Ⅱ)证明:由题设可得bn?q则
S2n?a1?a2q?a3q2?.....?a2nq2n?1, ①
T2n?a1?a2q?a3q2?a4q3?.....?a2nq2n?1,S2n?T2n?2(a2q?a4q?...?a2nq
① 式加上②式,得
3
2n?1
)
②
22n?2
S2n?T2n?2(a1?a3q?....?a2n?1q) ③
② 式两边同乘q,得
32n?1
q(S2n?T2n)?2(a1q?a3q?....?a2n?1q)
所以,
(1?q)S2n?(1?q)T2n?(S2n?T2n)?q(S2n?T2n)
?2d(q?q3?
?q2n?1)
2dq(1?q2n)*
?,n?N
1?q2
?(akn?aln)bn ?(kn?ln)db1qn?1
(Ⅲ)证明:c1?c2?(ak1?al1)b1?(ak2?al2)b2? ?(k1?l1)db1?(k2?l2)db1q?
因为d?0,b1?0,所以
c1?c2
?(k1?l1)?(k2?l2)q?db1
?(kn?ln)qn?1
(1) 若kn?ln,取i?n
(2) 若kn?ln,取i满足ki?li且kj?lj,i?1?j?n 由(1),(2)及题设知,1?i?n且 c1?c2?(k1?l1)?(k2?l2)q?db1(ki?1?li?1)qi?2?(ki?li)qi?1
① 当ki?li时,得ki?li??1,由q?n,得ki?li?q?1,i?1,2,3.....i?1 即k1?l1?q?1,(k2?l2)q?q(q?1)…,(ki?1?li?1)q又(ki?li)qi?1i?2?qi?2(q?1) ??qi?1,所以
c?c 12?(q?1)?(q?1)q?db1(q?1)qi?2?qi?11?qi?1?(q?1) 1?q因此c1?c2?0,即c1?c2
② 当ki?li同理可得综上,c1?c2
3.设m个不全相等的正数a1,a2,
(1)若m?2009,且a1,a2,,am(m?7)依次围成一个圆圈. ,a1006c1?c2??1,因此c1?c2 db1,a1005是公差为d的等差数列,而a1,a2009,a2008,是公比为q?d的等比数列;数列a1,a2,,am的前n项和 Sn(n?m)满足:S3?15,S2009?S2007?12a1,求通项an(n?m);
(2)若每个数an(n?m)是其左右相邻两数平方的等比中项,求证:
a1?2?a6?a7?2?am?ma1a2am; 2 解:(I)因a1,a2009,a2008,???,a1006是公比为d的等比数列,从而a2000?a1d,a2008?a1d
由S2009?S2008?12a1得a2008?a2009?12a1 ,故 解得d?3或d??4(舍去)。因此d?3S3?3a1?3d?15,解得a1?2 从而当n?1005时,an?a1?(n?1)d?2?3(n?1)?3n?1 当1006?n?2009时,由a1,a2009,a2008,???,a1006是公比为d的等比数列得
an?a1d2009?(n?1)?a1d2010?n(1006?n?2009)
?3n?1,n?1005因此an??2009?n ,1006?n?2009?2?3
22222222(II)由题意an?an?1an?1(1?n?m),am?am?1a1,a1?ama2得
① ?an?an?1an?1(1?n?m),??am?am?1a1 ② ?a?aa ③m2?1
有①得a3?a2a11,a4?,a5?,a6?1 ④ a3a1a2a2
2由①,②,③得a1a2???an?(a1a2???an),
故a1a2???an?1. ⑤ 又ar?3?ar?2ar?111???(1?r?m?3),故有 ar?1arar?1ar
ar?6?1?ar(1?r?m?6).⑥ ar?3
下面反证法证明:m?6k
1?p?5 若不然,设m?6k?p,其中
若取p?1即m?6k?1,则由⑥得am?a6k?1?a1,而由③得am?
am,从而a6?a6k?am?1,而 a1a1a,故a1?1, a2a2得a2?1,由②得am?1?
a6?a1,故a1?a2?1,由④及⑥可推得an?1(1?n?m)与题设矛盾 a2
同理若P=2,3,4,5均可得an?1(1?n?m)与题设矛盾,因此m?6k为6的倍数。由均值不等式得
a1?a2?a3??a6?(a1?aa11)?(a2?)?(2?1)?6 a1a2a1a2由上面三组数内必有一组不相等(否则a1?a2?a3?1,从而a4?a5??am?1与
题设矛盾),故等号不成立,从而a1?a2?a3?
又m?6k,由④和⑥得
2a7?22?am?(a7?2?a12)?2?(a6k?5?
2?a6)2?a6k)?a6?6
=(k-1) (a12?
=(k-1) (a12?
因此由⑤得
a1?a2?a3?2?a6?a7? 11122+a?+a?)?6(k-1)2322a12a2a32?am?6?6(k?1)?6k?m?ma1a2a3am
【类型2】
1.设数列?an?的前n项和为Sn,对任意的正整数n,都有an?5Sn?1成立,记bn?4?an(n?N*)。 1?an
(I)求数列?an?与数列?bn?的通项公式;
(II)设数列?bn?的前n项和为Rn,是否存在正整数k,使得Rn?4k成立?若
存在,找出一个正整数k;若不存在,请说明理由;
*(III)记cn?b2n?b2n?1(n?N),设数列?cn?的前n项和为Tn,求证:对任意正
整数n都有Tn?3; 2
解:(I)当n?1时,a1?5S1?1,?a1??1 4
an?11?? an4又an?5Sn?1,an?1?5Sn?1?1?an?1?an?5an?1,即
∴数列?an?是首项为a1??11q??,公比为的等比数列, 44
1n4?(?)1n(n?N*) ∴an?(?),bn?141?(?)n
4
(II)不存在正整数k,使得Rn?4k成立。
14?(?)n54?4?证明:由(I)知bn? n1n(?4)?11?(?)4
552015?16k?40b2k?1?b2k?8???8?k??8?k?8. (?4)2k?1?1(?4)2k?116?116k?4(16?1)(16k?4)5
∴当n为偶数时,设n?2m(m?N?) ∴Rn?(b1?b2)?(b3?b4)??(b2m?1?b2m)?8m?4n
当n为奇数时,设n?2m?1(m?N?)
∴Rn?(b1?b2)?(b3?b4)??(b2m?3?b2m?2)?b2m?1?8(m?1)?4?8m?4?4n ∴对于一切的正整数n,都有Rn?4k ∴不存在正整数k,使得Rn?4k成立。
(III)由bn?4?5得 n(?4)?1
5515?16n15?16n15?16n15cn?b2n?1?b2n?2n?2n?1????nnnn2nn24?14?1(16?1)(16?4)(16)?3?16?4(16)16
又b1?3,b2?134,?c2?, 33
3; 2当n?1时,T1?
当n?2时,
411Tn??25?(2?3?3161611n?2[1?()]2141616?n)??25?11631?161
2469316??25???148231?16
2.等比数列{an}的前n 项和为sn,已知S1,S3,S2成等差数列 (1)求{an}的公比q;
(2)求a1-a3=3,求sn
解:(Ⅰ)依题意有a1?(a1?a1q)?2(a1?a1q?a1q2) 由于 a1?0,故 2q2?q?0
1 又q?0,从而q?- 2
12(?)?3 (Ⅱ)由已知可得a1?a12
1n(41?(?))81n?1?(?)) 故a1?4,从而Sn? . 1321?(?)2
【类型3】
1.设数列{an}的前n项和为Sn, 已知a1?1,Sn?1?4an?2 (I)设bn?an?1?2an,证明数列{bn}是等比数列 (II)求数列{an}的通项公式。
解:由a1?1,及Sn?1?4an?2,有a1?a2?4a1?2,a2?3a1?2?5,?b1?a2?2a1?3
由Sn?1?4an?2,...① 则当n?2时,有Sn?4an?1?2.....② ②-①得an?1?4an?4an?1,?an?1?2an?2(an?2an?1) 又bn?an?1?2an,?bn?2bn?1?{bn}是首项b1?3,公比为2的等比数列.
n?1(II)由(I)可得bn?an?1?2an?3?2,?an?1an3?? 2n?12n4
?数列{an13是首项为,公差为的等比数列. 242n ?an1331n?2??(n?1)?n?,an?(3n?1)?2 n22444
an?an?1,n?N*. 21’a2?2,an+2=2.已知数列?an}满足, a1=
???令bn?an?1?an,证明:{bn}是等比数列; (Ⅱ)求?an}的通项公式。
解:(1)证b1?a2?a1?1,
当n?2时,bn?an?1?an?an?1?an11?an??(an?an?1)??bn?1, 222
1为公比的等比数列。 2所以?bn?是以1为首项,?
1n?1(2)由(1)知bn?an?1?an?(?), 2
当n?2时,an?a1?(a2?a1)?(a3?a2)?1?(an?an?1)?1?1?(?)?21?(?)n?2 2
11?(?)n?121521?1?[1?(?)n?2]??(?)n?1, ?1?323321?(?)2
5211?1521n?1n?1?(?)?1?aa??(?)(n?N*)。 当时,1,所以n332332
3.已知a1?1,a2?4,an?2?4an?1?an,bn?
(Ⅰ)求b1,b2,b3的值; an?1,n?N?. an
(Ⅱ)设cn?bnbn?1,Sn为数列?cn?的前n项和,求证:Sn?17n; (Ⅲ)求证:b2n?bn?11. 6417n?2
1772,b3? 417解:(Ⅰ)a2?4,a3?17,a4?72,所以b1?4.b2?
(Ⅱ)由an?2?4an?1?an得an?2a1?4?n即bn?1?4? an?1an?1bn所以,当n≥2时,bn?4于是c1?b1,b2?17,cn?bnbn?1?4bn?1?17(n≥2) 所以Sn?c1?c2??cn?17n
(Ⅲ)当n?1时,结论b2?b1?117?成立 464
当n≥2时,有bn?1?bn?|4?b?b111?4?|?|nn?1|≤|bn?bn?1| bnbn?1bnbn?117
≤1|bn?1?bn?2|≤172≤111|b?b|?2117n?16417n?2(n≥2)
所以, b2n?bn≤bn?1?bn?bn?2?bn?1??b2n?b2n?1
1?1n?11n()?()?4?1717?11()n?1(1?n)1?11717?11(n?N*) ?()2n?2??n?21176417?41?17
4.已知?an?是公差为d的等差数列,?bn?是公比为q的等比数列。
(1) 若an?3n?1,是否存在m、k?N,有am?am?1?ak?说明理由;
(2) 找出所有数列?an?和?bn?,使对一切n?N,**an?1?bn,并说明理由; an
(3) 若a1?5,d?4,b1?q?3,试确定所有的p,使数列?an?中存在某个连续p
项的和是数列?bn?中的一项,请证明。
[解法一](1)由am?am?1?ak,得6m?5?3k?1,整理后,可得k?2m?4, 3
m、k?N?,?k?2m为整数,?不存在m、k?N?,使等式成立。
a1?ndan?1?b1qn?1,?bn,(2) 若即 (*) a1?(n?1)da
n?1(ⅰ)若d?0,则1?b1q?bn。
当{an}为非零常数列,{bn}为恒等于1的常数列,满足要求.
(ⅱ)若d?0,(*)式等号左边取极限得lima1?nd?1,(*)式等号右n??a?(n?1)d1
边的极限只有当q?1时,才能等于1。此时等号左边是常数,?d?0,矛盾。 综上所述,只有当{an}为非零常数列,{bn}为恒等于1的常数列,满足要求.
【解法二】设an?nd?c,若an?1?bn,且?bn?为等比数列 an
则an?2an?1/?q,对n?N*都成立,即anan?2?qa2
n?1 an?1an
?(dn?c)(dn?2d?c)?q(dn?d?c)2对n?N*都成立,?a2?qd2....7分 (i)
(ii) *若d=0,则an?c?0,?bn?1,n?N 若d?0,则q=1,?bn?m(常数)即dn?d?c?m,则d=0,矛盾 dn?c
an?1?bn, an综上所述,有an?c?0,bn?1,使对一切n?N*,
n(3)an?4n?1,bn?3,n?N*
k*设am?1?am?2????am?p?bk?3,p、k?N,m?N.
4(m?1)?1?4(m?p)?1p?3k, 2
3k
?4m?2p?3?,?p、k?N*,?p?35,s?N. p
取k?3s?2,4m?32s?2?2?3s?3?(4?1)2s?2?2?(4?1)s?3?0, 由二项展开式可得正整数M1、M2,使得(4-1)2s+2=4M1+1, 2?(4?1)s?8M2?(?1)s2,
?4m?4(M1?2M2)?(?1)s?12,?存在整数m满足要求. ??
故当且仅当p=3s,s?N时,命题成立.
【类型4】
1n?11.已知数列?an?的前n项和Sn??an?()?2(n为正整数)2
n(Ⅰ)令bn?2an,求证数列?bn?是等差数列,并求数列?an?的通项公式;
(Ⅱ)令cn?n?15nan,Tn?c1?c2?........?cn比较Tn与的大小,并予以证明。 n2n?1
11解:(I)在Sn??an?()n?1?2中,令n=1,可得S1??an?1?2?a1,即a1? 22
11?an?Sn?Sn?1??an?an?1?()n?1, 当n?2时,Sn?1??an?1?()n?2?2,2
?2aa1n?1
n?n?

1?(2),即2nan?2n?1an?1?1.
bn
n?2an,?bn?bn?1?1,即当n?2时,bn?bn?1?1
又b1?2a1?1,?数列?bn?是首项和公差均为1的等差数列. 于是bn
n?1?(n?1)?1?n?2nan,?an?2n.
(II) 由(I)得cn?n?1
na?(n?1)(1
n2)n,所以
T111
n?2?2?3?(2)2?4?(2)3??(n?1)(1
2)n
1
2T2?(1
2)2?3?(11
n?2)3?4?(2)4??(n?1)(1
2)n?1
由①-②得1
2T?(1213
n?12)?(2)??(11
2)n?(n?1)(2)n?11[1?(1)n?1
]
?1??(n?1)(1)n?1?3?n?3
1?1222n?1
2
?Tn?3
n?3?2n
T5nn?35n(n?3)(2n?2n?1)
n?2n?1?3?2n?2n?1?2n(2n?1)
于是确定Tn
n与5
2n?1的大小关系等价于比较2n与2n?1的大小
由2?2?1?1;22?2?2?1;23?2?3?1;24?2?4?1;25?2?5;可猜想当n?3时,2n?2n?1.证明如下: 2
证法1:(1)当n=3时,由上验算显示成立。
(2)假设n?k?1时,则
2k?1?22k?2(2k?1)?4k?2?2(k?1)?1?(2k?1)?2(k?1)?1 所以当n?k?1时猜想也成立
n综合(1)(2)可知 ,对一切n?3的正整数,都有2?2n?1.
证法2:当n?3时
0122n?(1?1)n?Cn?Cn?Cn?n?1n01n?1n?Cn?Cn?Cn?Cn?Cn?Cn?2n?2?2n?1
综上所述,当n?1,2时Tn?5n5n,当n?3时Tn? 2n?12n?1
【类型5】
1. 已知数列?xn}满足, x1=11xn+1=,n?N*. 2’1?xn
???猜想数列{xn}的单调性,并证明你的结论;
12n?1(Ⅱ)证明:|xn?1-xn|≤()。65
112513x?及x?得x??x?,x?证(1)由1 n+124421?xn3821
由x2?x4?x6猜想:数列?x2n?是递减数列
下面用数学归纳法证明:
(1)当n=1时,已证命题成立 (2)假设当n=k时命题成立,即x2k?x2k?2
易知x2k?0,那么x2k?2?x2k?4?x2k?3?x2k?111?? 1?x2k?11?x2k?3(1?x2k?1)(1?x2k?3) =x2k?x2k?2?0 (1?x2k)(1?x2k?1)(1?x2k?2)(1?x2k?3)
即x2(k?1)?x2(k?1)?2
也就是说,当n=k+1时命题也成立,结合(1)和(2)知,命题成立
(2)当n=1时,xn?1?xn?x2?x1?1,结论成立 6
当n?2时,易知0?xn?1?1,?1?xn?1?2,xn?11? 1?xn?12
?(1?xn)(1?xn?1)?(1?15)(1?xn?1)?2?xn?1? 1?xn?12
?xn?1?xn?xn?xn?111?? 1?xn1?xn?1(1?xn)(1?xn?1)
2n-1?()x2?x15222xn?xn?1?()xn?1?xn?2?55 12n-1?)65?2.对于数列{un},若存在常数M>0,对任意的n?N,恒有 *
un?1?un?un?un?1??u2?u1?M, 则称数列{un}为B?数列.
1的等比数列是否为B-数列?请说明理由; 2(Ⅰ)首项为1,公比为?
(Ⅱ)设Sn是数列{xn}的前n项和.给出下列两组判断:
A组:①数列{xn}是B-数列, ②数列{xn}不是B-数列;
B组:③数列{Sn}是B-数列, ④数列{Sn}不是B-数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题. 判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列{an}是B-数列,证明:数列{an}也是B-数列。
1n?1解: (Ⅰ)设满足题设的等比数列为{an},则an?(?).于是: 2
1131an?an?1?(?)n?1?(?)n?2??()n?2,n?2. 22222
|an?1?an|?|an?an?1|?
3?112?1??()?=?2?22?|a2?a1| 1n-1?1n???()3?1?()??3. =??22???
所以首项为1,公比为?1的等比数列是B-数列 . 2
(Ⅱ)命题1:若数列{xn}是B-数列,则数列{Sn}是B-数列.此命题为假命题.
事实上设xn=1,n?N,易知数列{xn}是B-数列,但Sn=n, |Sn?1?Sn|?|Sn?Sn?1|??|S2?S1|?n. *
由n的任意性知,数列{Sn}不是B-数列。 命题2:若数列{Sn}是B-数列,则数列{xn}不是B-数列。此命题为真命题。 事实上,因为数列{Sn}是B-数列,所以存在正数M,对任意的n?N,有 |Sn?1?Sn|?|Sn?Sn?1|?
即|xn?1|?|xn|??|S2?S1|?M, *?|x2|?M.于是xn?1?xn?xn?xn?1??x2?x1
?xn?1?2xn?2xn?1??2x2?x1?2M?x1, 所以数列{xn}是B-数列。
(Ⅲ)若数列?an?是B-数列,则存在正数M,对任意的n?N?,有 an?1?an?an?an?1??a2?a1?M.
?a2?a1?a1
?a2?a1?a1?M?a1. 因为an?an?an?1?an?1?an?2? ?an?an?1?an?1?an?2?
22记K?M?a1,则有an?1?an?(an?1?an)(an?1?an)
?(an?1?an)an?1?an?2Kan?1?an.
2222222因此an?1?an?an?an?1?...?a2?a1?2KM,故数列?an?是B-数列。
