椭圆的基本知识
1.椭圆的定义:把平面内与两个定点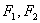 的距离之和等于常数(大于
的距离之和等于常数(大于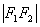 )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做焦距(设为2c).
)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做焦距(设为2c).
2.椭圆的标准方程:

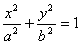 (
(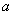 >
>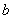 >0)
>0)  (
(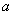 >
>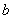 >0)
>0)
焦点在坐标轴上的椭圆标准方程有两种情形,为了计算简便,可设方程为mx2+ny2=1(m>0,n>0)不必考虑焦点位置,求出方程
3.求轨迹方程的方法: 定义法、待定系数法、相关点法、直接法
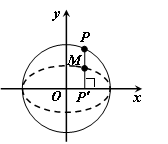
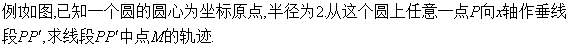 解:(相关点法)设点M(x, y),点P(x0, y0),
解:(相关点法)设点M(x, y),点P(x0, y0),
则x=x0, y= 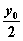 得x0=x, y0=2y.
得x0=x, y0=2y.
∵x02+y02=4, 得 x2+(2y)2=4,
即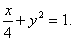 所以点M的轨迹是一个椭圆.
所以点M的轨迹是一个椭圆.
4.范围. x2≤a2,y2≤b2,∴|x|≤a,|y|≤b.
椭圆位于直线x=±a和y=±b围成的矩形里.
5.椭圆的对称性
椭圆是关于y轴、x轴、原点都是对称的.坐标轴是椭圆的对称轴.
原点是椭圆的对称中心.椭圆的对称中心叫做椭圆的中心.
6.顶点 只须令x=0,得y=±b,点B1(0,-b)、B2(0, b)是椭圆和y轴的两个交点;令y=0,得x=±a,点A1(-a,0)、A2(a,0)是椭圆和x轴的两个交点.椭圆有四个顶点:A1(-a, 0)、A2(a, 0)、B1(0, -b)、B2(0, b).椭圆和它的对称轴的四个交点叫椭圆的顶点.
线段A1A2、B1B2分别叫做椭圆的长轴和短轴.
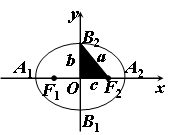 长轴的长等于2a. 短轴的长等于2b.a叫做椭圆的
长轴的长等于2a. 短轴的长等于2b.a叫做椭圆的
长半轴长.b叫做椭圆的短半轴长.
|B1F1|=|B1F2|=|B2F1|=|B2F2|=a.
在Rt△OB2F2中,|OF2|2=|B2F2|2-|OB2|2,
即c2=a2-b2.
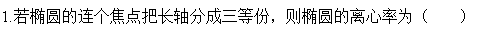
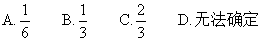

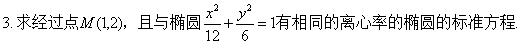


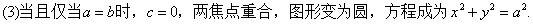
.

椭圆典型例题
例1 已知椭圆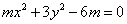 的一个焦点为(0,2)求
的一个焦点为(0,2)求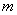 的值.
的值.
分析:把椭圆的方程化为标准方程,由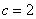 ,根据关系
,根据关系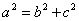 可求出
可求出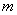 的值.
的值.
解:方程变形为 .因为焦点在
.因为焦点在 轴上,所以
轴上,所以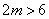 ,解得
,解得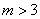 .
.
又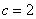 ,所以
,所以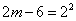 ,
,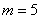 适合.故
适合.故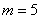 .
.
例2 已知椭圆的中心在原点,且经过点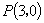 ,
,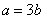 ,求椭圆的标准方程.
,求椭圆的标准方程.
分析:因椭圆的中心在原点,故其标准方程有两种情况.根据题设条件,运用待定系数法,
求出参数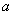 和
和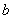 (或
(或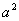 和
和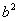 )的值,即可求得椭圆的标准方程.
)的值,即可求得椭圆的标准方程.
解:当焦点在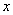 轴上时,设其方程为
轴上时,设其方程为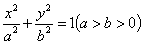 .
.
由椭圆过点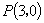 ,知
,知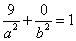 .又
.又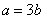 ,代入得
,代入得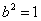 ,
,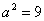 ,故椭圆的方程为
,故椭圆的方程为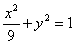 .
.
当焦点在 轴上时,设其方程为
轴上时,设其方程为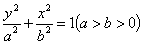 .
.
由椭圆过点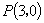 ,知
,知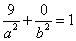 .又
.又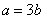 ,联立解得
,联立解得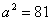 ,
,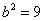 ,故椭圆的方程为
,故椭圆的方程为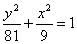 .
.
例3 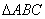 的底边
的底边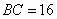 ,
, 和
和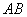 两边上中线长之和为30,求此三角形重心
两边上中线长之和为30,求此三角形重心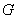 的轨迹和顶点
的轨迹和顶点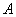 的轨迹.
的轨迹.
分析:(1)由已知可得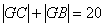 ,再利用椭圆定义求解.
,再利用椭圆定义求解.
(2)由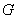 的轨迹方程
的轨迹方程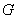 、
、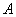 坐标的关系,利用代入法求
坐标的关系,利用代入法求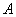 的轨迹方程.
的轨迹方程.
解: (1)以 所在的直线为
所在的直线为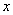 轴,
轴, 中点为原点建立直角坐标系.设
中点为原点建立直角坐标系.设 点坐标为
点坐标为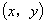 ,由
,由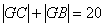 ,知
,知 点的轨迹是以
点的轨迹是以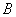 、
、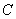 为焦点的椭圆,且除去轴上两点.因
为焦点的椭圆,且除去轴上两点.因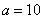 ,
, ,有
,有 ,
,
故其方程为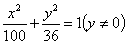 .
.
(2)设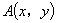 ,
,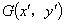 ,则
,则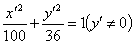 . ①
. ①
由题意有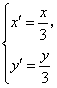 代入①,得
代入①,得 的轨迹方程为
的轨迹方程为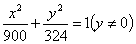 ,其轨迹是椭圆(除去
,其轨迹是椭圆(除去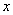 轴上两点).
轴上两点).
例4 已知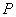 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点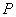 到两焦点的距离分别为
到两焦点的距离分别为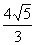 和
和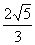 ,过
,过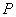 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
解:设两焦点为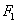 、
、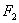 ,且
,且 ,
,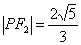 .从椭圆定义知
.从椭圆定义知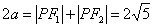 .即
.即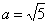 .
.
从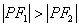 知
知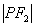 垂直焦点所在的对称轴,所以在
垂直焦点所在的对称轴,所以在 中,
中,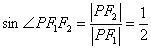 ,
,
可求出 ,
,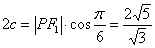 ,从而
,从而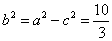 .
.
∴所求椭圆方程为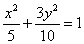 或
或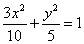 .
.
 例5 已知椭圆方程
例5 已知椭圆方程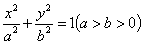 ,长轴端点为
,长轴端点为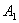 ,
,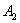 ,焦点为
,焦点为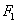 ,
,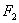 ,
,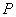 是椭圆上一点,
是椭圆上一点,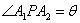 ,
, .求:
.求: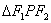 的面积(用
的面积(用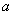 、
、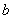 、
、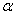 表示).
表示).
分析:求面积要结合余弦定理及定义求角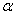 的两邻边,从而利用
的两邻边,从而利用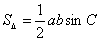 求面积.
求面积.
解:如图,设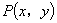 ,由椭圆的对称性,不妨设
,由椭圆的对称性,不妨设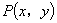 ,由椭圆的对称性,不妨设
,由椭圆的对称性,不妨设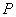 在第一象限.由余弦定理知:
在第一象限.由余弦定理知: 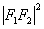
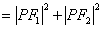
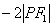 ·
·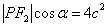 .①
.①
由椭圆定义知: 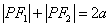 ②,则
②,则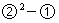 得
得 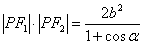 .
.
故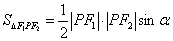
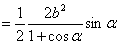
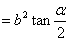 .
.
 例6 已知动圆
例6 已知动圆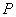 过定点
过定点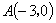 ,且在定圆
,且在定圆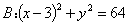 的内部与其相内切,求动圆圆心
的内部与其相内切,求动圆圆心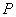 的轨迹方程.
的轨迹方程.
分析:关键是根据题意,列出点P满足的关系式.
解:如图所示,设动圆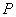 和定圆
和定圆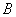 内切于点
内切于点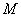 .动点
.动点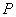 到两定点,
到两定点,
即定点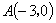 和定圆圆心
和定圆圆心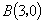 距离之和恰好等于定圆半径,
距离之和恰好等于定圆半径,
即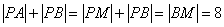 .∴点
.∴点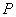 的轨迹是以
的轨迹是以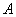 ,
,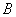 为两焦点,
为两焦点,
半长轴为4,半短轴长为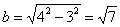 的椭圆的方程:
的椭圆的方程: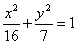 .
.
说明:本题是先根据椭圆的定义,判定轨迹是椭圆,然后根据椭圆的标准方程,求轨迹的方程.这是求轨迹方程的一种重要思想方法.
例7 已知椭圆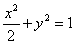
(1)求过点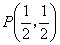 且被
且被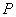 平分的弦所在直线的方程;
平分的弦所在直线的方程;
(2)求斜率为2的平行弦的中点轨迹方程;
(3)过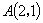 引椭圆的割线,求截得的弦的中点的轨迹方程;
引椭圆的割线,求截得的弦的中点的轨迹方程;
(4)椭圆上有两点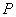 、
、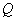 ,
,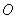 为原点,且有直线
为原点,且有直线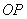 、
、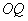 斜率满足
斜率满足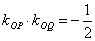 ,
,
求线段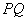 中点
中点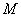 的轨迹方程.
的轨迹方程.
分析:此题中四问都跟弦中点有关,因此可考虑设弦端坐标的方法.
解:设弦两端点分别为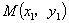 ,
,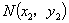 ,线段
,线段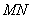 的中点
的中点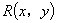 ,则
,则

(1)将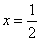 ,
,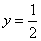 代入⑤,得
代入⑤,得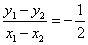 ,故所求直线方程为:
,故所求直线方程为: 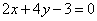 . ⑥
. ⑥
将⑥代入椭圆方程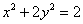 得
得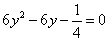 ,
,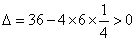 符合题意,
符合题意,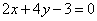 为所求.
为所求.
(2)将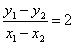 代入⑤得所求轨迹方程为:
代入⑤得所求轨迹方程为: 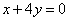 .(椭圆内部分)
.(椭圆内部分)
(3)将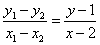 代入⑤得所求轨迹方程为:
代入⑤得所求轨迹方程为: 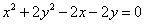 .(椭圆内部分)
.(椭圆内部分)
(4)由①+②得 : 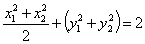 , ⑦, 将③④平方并整理得
, ⑦, 将③④平方并整理得
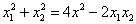 , ⑧,
, ⑧, 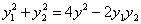 , ⑨
, ⑨
将⑧⑨代入⑦得: 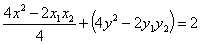 , ⑩
, ⑩
再将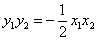 代入⑩式得:
代入⑩式得: 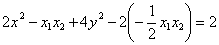 , 即
, 即  .
.
此即为所求轨迹方程.当然,此题除了设弦端坐标的方法,还可用其它方法解决.
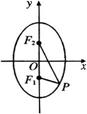 例8 已知椭圆
例8 已知椭圆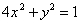 及直线
及直线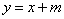 .
.
(1)当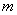 为何值时,直线与椭圆有公共点?
为何值时,直线与椭圆有公共点?
(2)若直线被椭圆截得的弦长为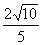 ,求直线的方程.
,求直线的方程.
解:(1)把直线方程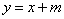 代入椭圆方程
代入椭圆方程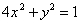 得
得 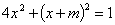 ,
,
即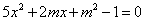 .
.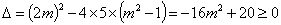 ,解得
,解得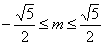 .
.
(2)设直线与椭圆的两个交点的横坐标为 ,
,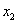 ,由(1)得
,由(1)得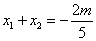 ,
,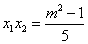 .
.
根据弦长公式得 :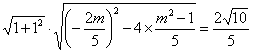 .解得
.解得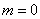 .方程为
.方程为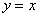 .
.
说明:处理有关直线与椭圆的位置关系问题及有关弦长问题,采用的方法与处理直线和圆的有所区别.
这里解决直线与椭圆的交点问题,一般考虑判别式 ;解决弦长问题,一般应用弦长公式.
;解决弦长问题,一般应用弦长公式.
用弦长公式,若能合理运用韦达定理(即根与系数的关系),可大大简化运算过程.
 例9 以椭圆
例9 以椭圆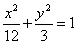 的焦点为焦点,过直线
的焦点为焦点,过直线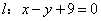 上一点
上一点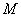 作椭圆,要使所作椭圆的长轴最短,点
作椭圆,要使所作椭圆的长轴最短,点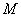 应在何处?并求出此时的椭圆方程.
应在何处?并求出此时的椭圆方程.
分析:椭圆的焦点容易求出,按照椭圆的定义,本题实际上就是要在已知直线上找一点,使该点到直线同侧的两已知点(即两焦点)的距离之和最小,只须利用对称就可解决.
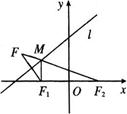
解:如图所示,椭圆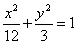 的焦点为
的焦点为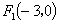 ,
, .
.
点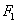 关于直线
关于直线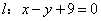 的对称点
的对称点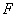 的坐标为(-9,6),直线
的坐标为(-9,6),直线 的方程为
的方程为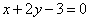 .
.
解方程组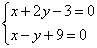 得交点
得交点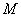 的坐标为(-5,4).此时
的坐标为(-5,4).此时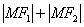 最小.
最小.
所求椭圆的长轴: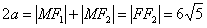 ,∴
,∴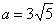 ,又
,又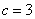 ,
,
∴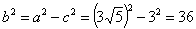 .因此,所求椭圆的方程为
.因此,所求椭圆的方程为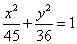 .
.
例10 已知方程 表示椭圆,求
表示椭圆,求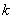 的取值范围.
的取值范围.
解:由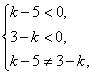 得
得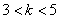 ,且
,且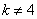 .
.
∴满足条件的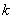 的取值范围是
的取值范围是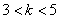 ,且
,且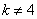 .
.
说明:本题易出现如下错解:由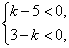 得
得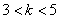 ,故
,故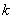 的取值范围是
的取值范围是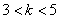 .
.
出错的原因是没有注意椭圆的标准方程中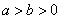 这个条件,当
这个条件,当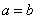 时,并不表示椭圆.
时,并不表示椭圆.
例11 已知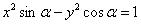
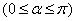 表示焦点在
表示焦点在 轴上的椭圆,求
轴上的椭圆,求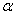 的取值范围.
的取值范围.
分析:依据已知条件确定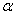 的三角函数的大小关系.再根据三角函数的单调性,求出
的三角函数的大小关系.再根据三角函数的单调性,求出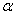 的取值范围.
的取值范围.
解:方程可化为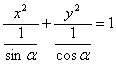 .因为焦点在
.因为焦点在 轴上,所以
轴上,所以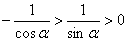 .
.
因此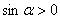 且
且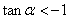 从而
从而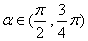 .
.
说明:(1)由椭圆的标准方程知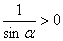 ,
,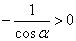 ,这是容易忽视的地方.
,这是容易忽视的地方.
(2)由焦点在 轴上,知
轴上,知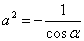 ,
,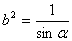 . (3)求
. (3)求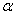 的取值范围时,应注意题目中的条件
的取值范围时,应注意题目中的条件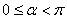 .
.
例12 求中心在原点,对称轴为坐标轴,且经过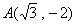 和
和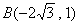 两点的椭圆方程
两点的椭圆方程
分析:由题设条件焦点在哪个轴上不明确,椭圆标准方程有两种情形,为了计算简便起见,
可设其方程为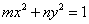 (
(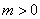 ,
,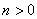 ),且不必去考虑焦点在哪个坐标轴上,直接可求出方程.
),且不必去考虑焦点在哪个坐标轴上,直接可求出方程.
解:设所求椭圆方程为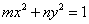 (
(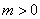 ,
,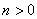 ).由
).由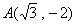 和
和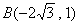 两点在椭圆上可得
两点在椭圆上可得
 即
即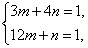 所以
所以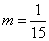 ,
,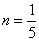 .故所求的椭圆方程为
.故所求的椭圆方程为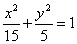 .
.
例13 已知长轴为12,短轴长为6,焦点在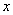 轴上的椭圆,过它对的左焦点
轴上的椭圆,过它对的左焦点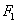 作倾斜解为
作倾斜解为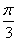 的直线交椭圆于
的直线交椭圆于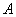 ,
,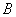 两点,求弦
两点,求弦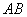 的长.
的长.
分析:可以利用弦长公式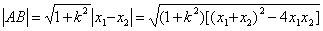 求得,
求得,
也可以利用椭圆定义及余弦定理,还可以利用焦点半径来求.
解:(法1)利用直线与椭圆相交的弦长公式求解.
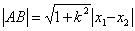
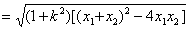 .因为
.因为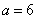 ,
,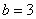 ,所以
,所以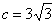 .因为焦点在
.因为焦点在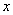 轴上,
轴上,
所以椭圆方程为 ,左焦点
,左焦点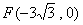 ,从而直线方程为
,从而直线方程为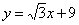 .
.
由直线方程与椭圆方程联立得: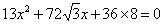 .设
.设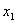 ,
,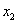 为方程两根,所以
为方程两根,所以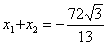 ,
,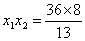 ,
, , 从而
, 从而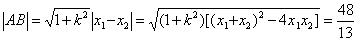 .
.
(法2)利用椭圆的定义及余弦定理求解.
由题意可知椭圆方程为 ,设
,设 ,
,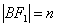 ,则
,则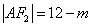 ,
,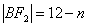 .
.
在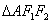 中,
中, ,即
,即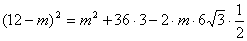 ;
;
所以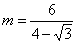 .同理在
.同理在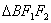 中,用余弦定理得
中,用余弦定理得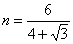 ,所以
,所以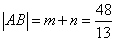 .
.
(法3)利用焦半径求解.
先根据直线与椭圆联立的方程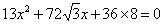 求出方程的两根
求出方程的两根 ,
,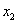 ,它们分别是
,它们分别是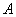 ,
,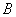 的横坐标.
的横坐标.
再根据焦半径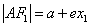 ,
,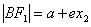 ,从而求出
,从而求出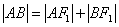 .
.
例14 椭圆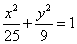 上的点
上的点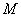 到焦点
到焦点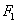 的距离为2,
的距离为2,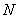 为
为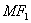 的中点,则
的中点,则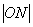 (
(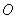 为坐标原点)的值为A.4 B.2 C.8 D.
为坐标原点)的值为A.4 B.2 C.8 D.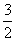

说明:(1)椭圆定义:平面内与两定点的距离之和等于常数(大于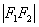 )的点的轨迹叫做椭圆.
)的点的轨迹叫做椭圆.
(2)椭圆上的点必定适合椭圆的这一定义,即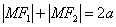 ,利用这个等式可以解决椭圆上的点与焦点的有关距离.
,利用这个等式可以解决椭圆上的点与焦点的有关距离.
例15 已知椭圆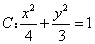 ,试确定
,试确定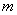 的取值范围,使得对于直线
的取值范围,使得对于直线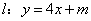 ,椭圆
,椭圆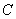 上有不同的两点关于该直线对称.
上有不同的两点关于该直线对称.
分析:若设椭圆上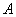 ,
,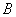 两点关于直线
两点关于直线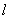 对称,则已知条件等价于:(1)直线
对称,则已知条件等价于:(1)直线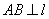 ;(2)弦
;(2)弦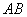 的中点
的中点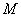 在
在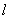 上.
上.
利用上述条件建立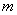 的不等式即可求得
的不等式即可求得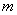 的取值范围.
的取值范围.
解:(法1)设椭圆上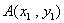 ,
,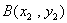 两点关于直线
两点关于直线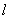 对称,直线
对称,直线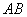 与
与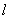 交于
交于 点.
点.
∵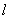 的斜率
的斜率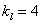 ,∴设直线
,∴设直线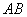 的方程为
的方程为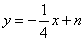 .由方程组
.由方程组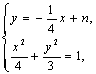 消去
消去 得
得
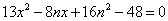 ①。∴
①。∴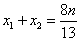 .于是
.于是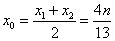 ,
,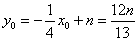 ,
,
即点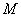 的坐标为
的坐标为 .∵点
.∵点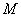 在直线
在直线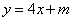 上,∴
上,∴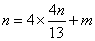 .解得
.解得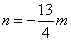 . ②
. ②
将式②代入式①得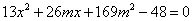 ③
③
∵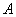 ,
,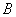 是椭圆上的两点,∴
是椭圆上的两点,∴ .解得
.解得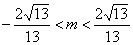 .
.
(法2)同解法1得出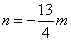 ,∴
,∴ ,
,
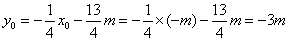 ,即
,即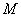 点坐标为
点坐标为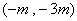 .
.
∵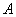 ,
,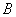 为椭圆上的两点,∴
为椭圆上的两点,∴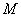 点在椭圆的内部,∴
点在椭圆的内部,∴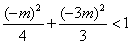 .解得
.解得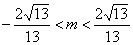 .
.
(法3)设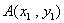 ,
,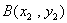 是椭圆上关于
是椭圆上关于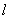 对称的两点,直线
对称的两点,直线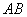 与
与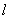 的交点
的交点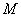 的坐标为
的坐标为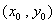 .
.
∵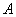 ,
,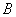 在椭圆上,∴
在椭圆上,∴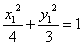 ,
,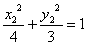 .两式相减得
.两式相减得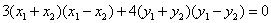 ,
,
即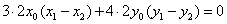 .∴
.∴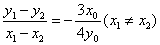 .
.
又∵直线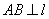 ,∴
,∴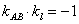 ,∴
,∴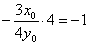 ,即
,即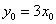 ①。
①。
又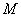 点在直线
点在直线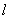 上,∴
上,∴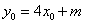 ②。由①,②得
②。由①,②得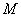 点的坐标为
点的坐标为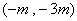 .以下同解法2.
.以下同解法2.
说明:涉及椭圆上两点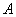 ,
,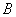 关于直线
关于直线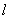 恒对称,求有关参数的取值范围问题,可以采用列参数满足的不等式:
恒对称,求有关参数的取值范围问题,可以采用列参数满足的不等式:
(1)利用直线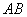 与椭圆恒有两个交点,通过直线方程与椭圆方程组成的方程组,消元后得到的一元二次方程的判别式
与椭圆恒有两个交点,通过直线方程与椭圆方程组成的方程组,消元后得到的一元二次方程的判别式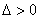 ,建立参数方程.
,建立参数方程.
(2)利用弦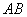 的中点
的中点 在椭圆内部,满足
在椭圆内部,满足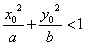 ,将
,将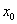 ,
,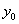 利用参数表示,建立参数不等式.
利用参数表示,建立参数不等式.
例17 在面积为1的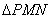 中,
中,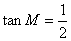 ,
,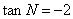 ,建立适当的坐标系,求出以
,建立适当的坐标系,求出以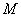 、
、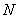 为焦点且过
为焦点且过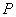 点的椭圆方程.
点的椭圆方程.
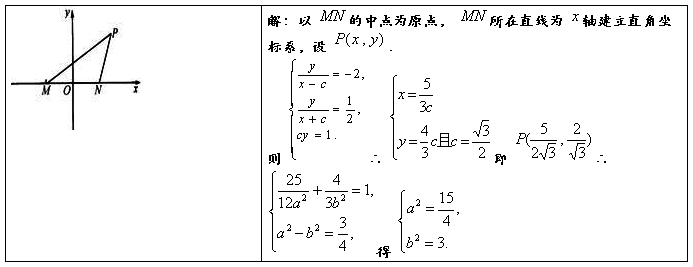
∴所求椭圆方程为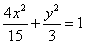
例18 已知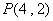 是直线
是直线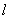 被椭圆
被椭圆 所截得的线段的中点,求直线
所截得的线段的中点,求直线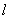 的方程.
的方程.
分析:本题考查直线与椭圆的位置关系问题.通常将直线方程与椭圆方程联立消去 (或
(或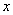 ),得到关于
),得到关于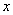 (或
(或 )的一元二次方程,再由根与系数的关系,直接求出
)的一元二次方程,再由根与系数的关系,直接求出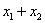 ,
,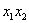 (或
(或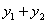 ,
,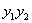 )的值代入计算即得.
)的值代入计算即得.
并不需要求出直线与椭圆的交点坐标,这种“设而不求”的方法,在解析几何中是经常采用的.
解:方法一:设所求直线方程为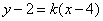 .代入椭圆方程,整理得
.代入椭圆方程,整理得
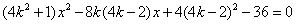 ①
①
设直线与椭圆的交点为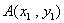 ,
,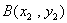 ,则
,则 、
、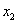 是①的两根,∴
是①的两根,∴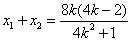
∵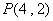 为
为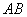 中点,∴
中点,∴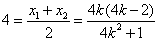 ,
,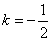 .∴所求直线方程为
.∴所求直线方程为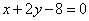 .
.
方法二:设直线与椭圆交点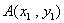 ,
,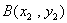 .∵
.∵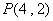 为
为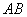 中点,∴
中点,∴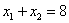 ,
,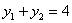 .
.
又∵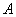 ,
,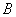 在椭圆上,∴
在椭圆上,∴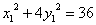 ,
,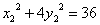 两式相减得
两式相减得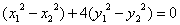 ,
,
即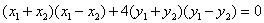 .∴
.∴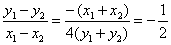 .∴直线方程为
.∴直线方程为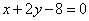 .
.
方法三:设所求直线与椭圆的一个交点为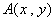 ,另一个交点
,另一个交点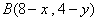 .
.
∵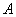 、
、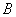 在椭圆上,∴
在椭圆上,∴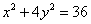 ①。
①。 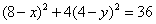 ②
②
从而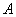 ,
,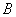 在方程①-②的图形
在方程①-②的图形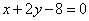 上,而过
上,而过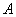 、
、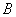 的直线只有一条,∴直线方程为
的直线只有一条,∴直线方程为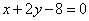 .
.
说明:直线与圆锥曲线的位置关系是重点考查的解析几何问题,“设而不求”的方法是处理此类问题的有效方法.
若已知焦点是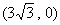 、
、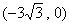 的椭圆截直线
的椭圆截直线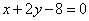 所得弦中点的横坐标是4,则如何求椭圆方程?
所得弦中点的横坐标是4,则如何求椭圆方程?
