第八章 图论
例1、下面哪些数的序列,可能是一个图的度数序列?如果可能,请试画出它的图. 哪些可能不是简单图?a) (1,2,3,4,5) b) (2,2,2,2,2) c) (1,2,3,2,4) d) (1,1,1,1,4) e) (1,2, 2,4,5)
解:a)不是, 因为有三个数字是奇数. b) c) d)是.
e) 不是简单图,因为它有5个结点, 有一个结点度为5, 必然有环或平行边.
例2、已知无向简单图G中,有10条边,4个3度结点,其余结点的度均小于或等于2,问G中至少有多少个结点?为什么?
解:已知边数|E|=10, ∑deg(v)=2|E|=20其中有4个3度结点, 余下结点度之和为: 20-3×4=8
因为G是简单图, 其余每个结点度数≤2, 所以至少还有4个结点.所以G中至少有8个结点.
强连通、单侧连通和弱连通
在简单有向图G中,如果任何两个结点间相互可达, 则称G是强连通. 如果任何一对结点间, 至少有一个结点到另一个结点可达, 则称G是单侧连通. 如果将G看成无向图后(即把有向边看成无向边)是连通的,则称G是弱连通.
在简单有向图中,具有强连通的最大子图,称为强分图.具有单侧连通的最大子图,称为单侧分图. 具有弱连通的最大子图,称为弱分图.
注:我每次都会被各种分图弄糊涂!!考试时要注意啊,千万不要错了
利用可达性矩阵求强分图,注意初等矩阵变换的知识不要忘了!!
令图G=<V,E,W>, 集合SiÍV Si’=V-Si , 令|V|=n
Si={u|从u0到u的最短路已求出}
Si’={u’|从u0到u’的最短路未求出}
Dijkstra算法:(求从u0到各点u的最短路长)
第一步. 置初值: d(u0,u0)=0 d(u0,v)=∞ (其中v≠ u0)
i=0 S0={u0} S0’=V-S0 ,
第二步.若 i=n-1 则停. 否则转第三步
第三步. 对每个u’∈Si’
计算 d(u0,u’)=min{d(u0,u’), d(u0,ui)+c(ui,u’)} ui ∈Si计算 min{d(u0,u’)}u’∈Si’
并用ui+1记下达到该最小值的那个结点u’
置Si+1 =Si∪{ui+1} i=i+1 Si’=V-Si , 转第二步.
例3、求最短路
解:例.求右图中从v1到v6的
最短路
1.置初值: u0=v1
d(u0,u0)=0
d(u0,v2)=d(u0,v3)=d(u0,v4)=d(u0,v5)=d(u0,v6)=∞
2.3. i=0 S0={v1} S0’={v2,v3,v4,v5,v6}
d(u0,v2)=min{d(u0,v2), d(u0,u0)+c(u0,v2)}=min{∞,0+3}=3
d(u0,v3)=min{d(u0,v3),d(u0,u0)+c(u0,v3)}=min{∞,0+∞}=∞
d(u0,v4)=min{d(u0,v4), d(u0,u0)+c(u0,v4)}=min{∞,0+5}=5
d(u0,v5)=min{d(u0,v5),d(u0,u0)+c(u0,v5)}=min{∞,0+∞}=∞
d(u0,v6)=min{d(u0,v6),d(u0,u0)+c(u0,v6)}=min{∞,0+∞}=∞
min{3,∞,5, ∞,∞}=3
ui+1 =u1=v2 , 实际已求出d(u0,v2)=3, 路是u0v2
i=1 S1={v1, v2}
S1’={v3,v4,v5,v6}
u1=v2
d(u0,u1)=3
d(u0,v3)=min{d(u0,v3),d(u0,u1)+c(u1,v3)}=min{∞,3+6}=9
d(u0,v4)=min{d(u0,v4), d(u0,u1)+c(u1,v4)}=min{5,3+1}=4
d(u0,v5)=min{d(u0,v5),d(u0,u1)+c(u1,v5)}=min{∞,3+∞}=∞
d(u0,v6)=min{d(u0,v6),d(u0,u1)+c(u1,v6)}=min{∞,3+∞}=∞
min{9,4,∞,∞}=4
ui+1 =u2=v4 , 实际已求出d(u0,v4)=4, 路是u0v2v4
i=2 S2={v1, v2 ,v4}
S2’={v3,v5,v6}
u2=v4
d(u0,u2)=4
d(u0,v3)=min{d(u0,v3), d(u0,u2)+c(u2,v3)}=min{9 ,4+3}=7
d(u0,v5)=min{d(u0,v5), d(u0,u2)+c(u2,v5)}=min{∞,4+1}=5
d(u0,v6)=min{d(u0,v6), d(u0,u2)+c(u2,v6)}=min{∞,4+∞}=∞
min{7,5,∞}=5
ui+1 =u3=v5 , 实际已求出d(u0,v5)=5, 路是u0v2v4 v5
i=3 S3={v1, v2 ,v4 ,v5}
S3’={v3,v6}
u3=v5
d(u0,u3)=5
d(u0,v3)=min{d(u0,v3),d(u0,u3)+c(u3,v3)}=min{7 ,5+3}=7
d(u0,v6)=min{d(u0,v6),d(u0,u3)+c(u3,v6)}=min{∞,5+6}=11
min{7,11}=7
ui+1 =u4=v3 , 实际已求出d(u0,v3)=7, 路是u0v2v4 v3
i=4 S3={v1, v2 ,v4 ,v5, v3} S3’={v6} u4=v3 d(u0,u4)=7
d(u0,v6)=min{d(u0,v6),d(u0,u4)+c(u4,v6)}=min{11,7+3}=10
min{10}=10
ui+1 =u5=v6 , 实际已求出d(u0,v6)=10, 路是u0v2v4 v3 v6
i=5 (n-1) 时 算法停止.
例4、求关键路径。
例如, 求右图的关键路径
(1)求各个结点的最早完成时间:
计算时,从前向后
逐个结点计算。
TE(v1)=0
TE(v2)=max{0+1}=1 (v1 - v2的先驱结点)
TE(v3)=max{0+2 ,1+0}=2 (v1v2 - v3的先驱结点)
TE(v4)=max{0+3,2+2}=4 (v1v3 - v4的先驱结点)
TE(v5)=max{1+3,4+4}=8 (v2v4 - v5的先驱结点)
TE(v6)=max{2+4,8+1}=9 (v3v5 - v6的先驱结点)
TE(v7)=max{1+4,2+4}=6 (v2v3 - v7的先驱结点)
TE(v8)=max{9+1,6+6}=12 (v6v7 - v8的先驱结点)
(2)求各个结点的最晚完成时间:
计算时,从后向前
逐个结点计算。
TL(v8)=TE(v8)=12
TL(v7)=min{12-6}=6 (v8)
TL(v6)=min {12-1}=11 (v8)
TL(v5)=min {11-1}=10 (v6)
TL(v4)=min {10-4}=6 (v5)
TL(v3)=min {6-2, 11-4, 6-4}=2 (v4v6v7)
TL(v2)=min {2-0, 10-3, 6-4}=2 (v3v5v7)
TL(v1)=min {2-1, 2-2, 6-3}=0 (v2v3v4)
(3)求各个结点的缓冲时间
TS(vi)=TL(vi)-TE(vi)

关键路径为: v1v3v7v8
例5、设G是结点数n≥3的简单图,若边数m≥(1/2)(n-1)(n-2)+2,证明G中存在汉密尔顿回路。
证明:假设G不存在汉密尔顿回路(不是H图),由H图充分条件判定定理可知,G中必存在结 点u1、u2,使得deg(u1)+deg(u2)≤n-1,即关联这两个结点的边数最多为n-1。
在图G-{u1,u2}中:结点数为n-2, 边数≤(1/2)(n-2)(n-3)
G中边数 m≤(1/2)(n-2)(n-3)+(n-1) <(1/2)(n-2)(n-3)+n=(1/2)(n2-5n+6)+n
=(1/2)(n2-5n+6+2n) =(1/2)(n2-3n+6)
=(1/2)[(n2-3n+2)+4]= (1/2)(n2-3n+2)+2
= (1/2)(n-1)(n-2)+2
与已知矛盾,所以G中存在汉密尔顿回路。
例6、平面图的欧拉公式是d=m-n+2 (r=e-v+2)?简单平面图G中至少有一个结点的度小于几?
解:由欧拉公式 v-e+r=2,所以r=e-v+2 (d=m-n+2 )成立。简单平面图G中至少存在一个结点的度数小于6。
因为如果图G的结点数v≤6时,所有结点的度均小于等于5。结论显然成立。
当v≥7时,若所有结点的度均≥ 6时,则由定理8-1.1得
2e=Σdeg(vi)≥6v ,所以推出 e≥3v。
而由定理8-7.2(必要条件) 设G是有v 个结点、e条边的连通
简单平面图, 若v≥3, 则 e≤3v-6.
所以不可能所有结点的度均大于等于6。即G中至少存在一个结点的度数小于6。
例7、证明在n≥4的极大平面图中,每个结点的度都大于等于3。
证明:因为结点数n≥3的简单平面图为极大平面图的充
分且必要条件是,每个面的次数均为3。所以G中任何回路的长度均大于或等于3。于是任结点u,与u相邻接的结点都在某个回路C上,且此回路的长度必大于等于3,所以deg(u)≥3。
图论这一章,还有点割集,边割集,点连通度,边连通度,完全关联矩阵等知识点,你可能还不熟,(应该不是考试的重点)注意及时复习啊!!!!想一下,还有一周左右的时间就要考试了。
第二篇:离散数学(二元关系)课后总结
第四章 二元关系
例1 设A={0,1},B={a,b},求A´B , B´A,A´A 。
解: A´B={<0,a>,<0,b>,<1,a>,<1,b>}
B´A={<a,0>,<b,0>,<a,1>,<b,1>}
A´A={<0,0>,<0,1>,<1,0>,<1,1>}
可见 A×B≠B×A
例2、关于笛卡尔乘积的几个证明
1)如果A、B都是有限集,且|A|=m, |B|=n,则
|A´B |=mn.
证明:由笛卡尔积的定义及排列组合中的乘法原理,直接推得此定理。
2) A´Φ=Φ´B=Φ
3) ´对∪和∩满足分配律。
设A,B,C是任意集合,则
⑴ A´(B∪C)= (A´B)∪(A´C);
⑵ A´(B∩C)= (A´B)∩(A´C);
⑶ (A∪B)´C= (A´C)∪(B´C);
⑷ (A∩B)´C= (A´C)∩(B´C)
证明 ⑴ :任取<x,y>ÎA´(B∪C)
ÛxÎA ÙyÎB∪C ÛxÎA Ù(yÎB∨yÎC)
Û( xÎA ÙyÎB)∨(xÎAÙyÎC)
Û<x,y>ÎA´B∨<x,y>ÎA´C
Û<x,y>Î(A´B)∪(A´C) 所以⑴式成立。
4)若C¹F,,则AÍBÛ(A´CÍB´C) Û(C´AÍC´B).
证明: 必要性:设AÍB,求证 A´CÍB´C
任取<x,y>ÎA´C ÛxÎAÙyÎCÞxÎBÙyÎC (因AÍB)
Û<x,y>ÎB´C 所以, A´CÍB´C.
充分性: 若CF¹, 由A´CÍB´C 求证 AÍB
取C中元素y, 任取 xÎAÞxÎAÙyÎCÛ<x,y>ÎA´C
Þ<x,y>ÎB´C (由A´CÍB´C )
ÛxÎBÙyÎCÞ xÎB 所以, AÍB.
所以 AÍBÛ(A´CÍB´C)
类似可以证明 AÍB Û(C´AÍC´B).
5) 设A、B、C、D为非空集合,则
A´BÍC´DÛAÍC∧BÍD.
证明: 首先,由A´BÍC´D 证明AÍC∧BÍD.
任取xÎA,任取yÎB,所以 xÎAÙyÎB
Û<x,y>ÎA×B
Þ<x,y>ÎC×D (由A´BÍC´D )
ÛxÎCÙyÎD 所以, AÍC∧BÍD.
其次, 由AÍC,BÍD. 证明A´BÍC´D
任取<x,y>ÎA×B
<x,y>ÎA×B Û xÎAÙyÎB
Þ xÎCÙyÎD (由AÍC,BÍD)
Û<x,y>ÎC×D 所以, A´BÍC´D 证毕.
例3、令A={1,2,3}给定A上八个关系如下:
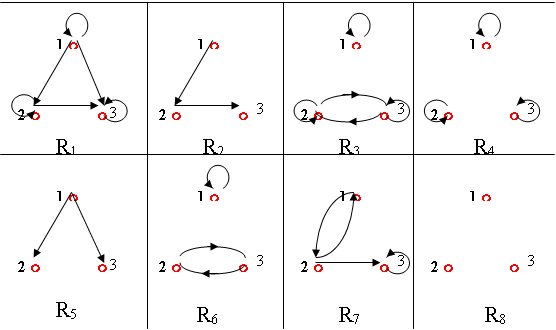
可见这八个关系中R1、R3、R4是自反的。R2、R5、 R8、均是反自反关系。R3、R4、 R6 、 R8均是对称关系。R1、R2、R4、R5、R8均是反对称关系。R4、R8既是对称也是反对称的。有些关系既不是对称也不是反对称的:如R7 。R1、R3、R4、R5、R8均是传递的关系。

注:对于传递性的理解还不够透彻,如果出题,自己可能会出错!!!
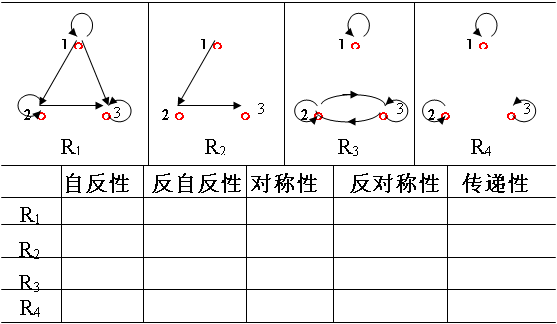
例4、A={1,2,3},给定A中五个关系如下:
R={<1,1>,<1,2>,<1,3>,<3,3>}
S={<1,1>,<1,2>,<2,1>,<2,2>,<3,3>}
T={<1,1>,<1,2>,<2,2>,<2,3>}
Φ
A×A
判断它们的性质:Y表示“是”,N表示“否”,填下表。

例5、令I是整数集合,I上关系R定义为:R={<x,y>|x-y可被3整除},求证R是自反、对称和传递的。
证明:⑴证自反性:任取x∈I, (要证出<x,x>ÎR )
因 x-x=0, 0可被3整除,所以有<x,x>∈R, 故R自反。
⑵证对称性:任取x,y∈I,设<x,y>∈R, (要证出 <y,x>ÎR )
由R定义得 x-y可被3整除, 即x-y=3n(n∈I), y-x=-(x-y)=-3n=3(-n), 因-n∈I, ∴<y,x>∈R, 所以R对称。
⑶证传递性:任取x,y,z∈I,设xRy, yRz, (要证出xRz)
由R定义得 x-y=3m, y-z=3n (m.n∈I)
x-z= (x-y)+(y-z)=3m+3n=3(m+n), 因m+n∈I,
所以xRz, 所以R传递。证毕
例6、设R是集合A上的一个自反关系,求证:R是对称和传递的,当且仅当<a,b>和<a,c>在R中,则有<b,c>也在R中。
证明:必要性: 已知R是对称和传递的。
分析:结论是个蕴含式,即<a,b>ÎR Ù <a,c>ÎR Þ <b,c>ÎR
可利用 “假设前件为真,推出后件为真 ” 方法证明。再结合已知条件:R对称、R传递。
设<a,b>ÎR 又<a,c>ÎR,(要证出 <b,c>ÎR )
因R对称的,故<b,a>ÎR,又已知<a,c>ÎR 由传递性得<b,c>ÎR。
所以有如果<a,b>和<a,c>在R中,则有<b,c>也在R中。
充分性: 已知任意 a,b,cÎA, 如<a,b>和<a,c>在R中,则有<b,c>也在R中。先证R对称:
分析:即任取 a,bÎA 设<a,b>ÎR Þ <b,a>ÎR
应有<?,b>ÎR Ù <?,a>ÎR Þ <b,a>ÎR 而已知<a,b>ÎR ,那么是否<a,a>ÎR ?
任取 a,bÎA 设<a,b>ÎR,(要证出 <b,a>ÎR )
因R是自反的,所以<a,a>ÎR,
由<a,b>ÎR且<a,a>ÎR,根据已知条件得<b,a>ÎR ,所以R是对称的。
再证R传递:
分析:即任取 a,b,cÎA 设<a,b>ÎR Ù <b,c>ÎR Þ <a,c>ÎR
应有<?,a>ÎR Ù <?,c>ÎR Þ <a,c>ÎR
而已知<b,c>ÎR ,那么是否<b,a>ÎR ?
任取 a,b,cÎA 设<a,b>ÎR,<b,c>ÎR。(要证出<a,c>ÎR )
由R是对称的,得<b,a>ÎR ,
由<b,a>ÎR且<b,c>ÎR,根据已知条件得
<a,c>ÎR , 所以R是传递的。
例7、给定A={1,2,3},A中关系R和S如下:
R={<1,1>,<1,2>,<1,3>,<3,3>}
S={<1,1>,<1,2>,<2,1>,<2,2>,<3,3>}
分别求复合关系RoS, SoR,IAoR, RoIA 。
解:RoS={<1,1>,<1,2>,<1,3>,<3,3>}
SoR={<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,3>}
IA={<1,1>,<2,2>,<3,3>}
IAoR=RoIA=R
例8、设F表示父亲和儿子之间的关系,M表示母亲和儿子之间的关系,S表示儿子和母亲之间的关系,D表示女儿和母亲之间的关系。问:F o F,F o S,D o( D o M)分别表示什么关系?
答: F o F表示祖孙关系。
F o S表示夫妻关系。
D o( D o M)表示外甥女和舅舅之间的关系。
例9、证明若RÍA×B ,SÍB×C TÍC×D则Ro(SoT)=(RoS)oT
证明:任取<a,d>∈Ro(SoT)
$Ûb(b∈B∧<a,b>∈R∧<b,d>∈SoT)
$Ûb(b∈B∧<a,b>∈R∧$c(c∈C∧<b,c>∈S∧<c,d>∈T))
$Ûb$c(b∈B∧<a,b>∈R∧(c∈C∧<b,c>∈S∧<c,d>∈T))
$Ûc$b(c∈C∧(b∈B∧<a,b>∈R∧<b,c>∈S∧<c,d>∈T))
$Ûc (c∈C∧$b(b∈B∧<a,b>∈R∧<b,c>∈S)∧<c,d>∈T)
$Ûc (c∈C∧<a,c>∈(RoS)∧<c,d>∈T)
Û<a,d>∈(RoS)oT
所以 Ro(SoT)=(RoS)oT
例10、 RÍA×B SÍB×C TÍB×C
⑴ Ro(S∪T)=(RoS)∪(RoT)
⑵ Ro(S∩T)Í(RoS)∩(RoT)
证明⑴ 任取<a,c>∈Ro(S∪T)
Û $b(b∈B∧<a,b>∈R∧<b,c>∈S∪T)
$Ûb(b∈B∧<a,b>∈R∧(<b,c>∈S∨<b,c>∈T))
$Ûb((b∈B∧<a,b>∈R∧<b,c>∈S)∨(b∈B∧<a,b>∈R∧<b,c>∈T))
$Ûb(b∈B∧<a,b>∈R∧<b,c>∈S)∨ $b(b∈B∧<a,b>∈R∧<b,c>∈T)
Û<a,c>∈RoS∨<a,c>∈RoT
Û<a,c>∈(RoS)∪(RoT)
所以Ro (S∪T)=(RoS)∪(RoT)
证明⑵ 任取<a,c>∈Ro (S∩T)
Û $b(b∈B∧<a,b>∈R∧<b,c>∈S∩T)
$Ûb(b∈B∧<a,b>∈R∧(<b,c>∈S∧<b,c>∈T))
$Ûb((b∈B∧<a,b>∈R∧<b,c>∈S) ∧ (b∈B∧<a,b>∈R∧<b,c>∈T))
Þ$b(b∈B∧<a,b>∈R∧<b,c>∈S)∧$b(b∈B∧<a,b>∈R∧<b,c>∈T)
Û<a,c>∈RoS ∧<a,c>∈RoT
Û<a,c>∈(RoS)∩(RoT)
所以 Ro (S∩T)Í(RoS)∩(RoT)
$x(A(x)∧B(x)) Þ$xA(x)∧$xB(x)
求传递闭包以及可达矩阵
求t(R)的矩阵Warshall算法:|X|=n, RÍX×X, 令MR=A R2的矩阵为A(2),… Rk的矩阵为A(k) .故t(R)的矩阵记作MR+=A+A(2) +…+A(k)+…(“+”是逻辑加)
⑴置新矩阵 A :=MR ;
⑵置 i=1;
⑶对所有 j ,如果A[j,i] =1 ,则对k=1,2,…,n
A[j,k]:=A[j,k]+A[i,k]; /*第j行+第i行,送回第j行*/
⑷ i加1;
⑸ 如果i≤n, 则转到步骤⑶,否则停止。
例11、令X={1,2,3,4}, X中关系R图如图所示,用此算法求t(R)的矩阵。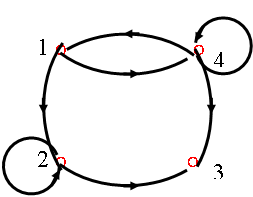

后续过程很简单,自己按所给步骤画画。
例12、给定A中关系R如上图所示,分别画出r(R)、s(R) 、t(R)、sr(R)、rs(R)、 tr(R)、rt(R)、st(R) 、ts(R) 的图。
例13、X={1,2,3}, A1={{1,2,3}}, A2={{1},{2},{3}},A3={{1,2},{3}}, A4={{1,2},{2,3}}, A5={{1},{3}},哪些是覆盖,哪些是划分?
解:A1, A2 ,A3 ,A4 是覆盖。 A1, A2 ,A3也是划分。
例14、A={1,2,3}下面是A中关系:

思考题:A={1,2,3},可构造多少个A中不同的等价关系?可以根据等价关系有向图的特点来考虑。
解:如果等价关系R中有三个独立子图的情形,则有1个等价关系。二个独立子图的情形时3个等价关系,一个独立子图时,1个等价关系。一共有5个不同的等价关系。
以下是关于商集的一个例子A={1,2,3,4,5,6,7} , R上模3同余关系,则商集 A/R= {[1]R,[2]R,[3]R} ={{1.4.7},{2,5},{3,6}}。
例15、集合A上的等价关系R,决定了A的一个划分,该划分就是商集A/R.
证明:由等价类性质可得 :
1) A/R中任意元素[a]R,有[a]RÍA.
2) 设[a]R,[b]R是A/R的两个不同元素,有 [a]RÇ[b]R=Φ
3) 因为A中每个元素都属于一个等价类,所以所有等价类的并集必等于A。
所以商集A/R是A的一个划分。
R图中每个独立子图上的结点,构成一个等价类。不同的等价类个数=独立子图个数。
例16、集合X的一个划分可以确定X上的一个等价关系。
证明:假设A={A1, A2,... ,An}是X的一个划分,如下构造
X 上的一个等价关系R: R=A12∪A22∪…∪An2 其中Ai2=Ai×Ai (i=1,2…n).
1) 证R自反:任取a∈X,因为A是X的划分,必存在
AiÎA使aÎAi ,于是<a,a>∈Ai×Ai , 又Ai×Ai ÍR∴有aRa。
2) 证R对称:任取a,b∈X, 设aRb,必存在AiÎA使得
<a,b>∈Ai×Ai ,于是a,bÎAi , \bRa, R是对称的。
3) 证R传递:任取a,b,c∈X, 设aRb,bRc, 必存在AiÎA
使得<a,b>∈Ai×Ai ,<b,c>∈Ai×Ai ,
(不可能有另一个划分块AkÎA使得<b,c>∈Ak×Ak, 因为
如果这样,就使得, 既b∈Ai又bÎAk ,与A是划分矛盾。)
于是a,b,cÎAi , 所以<a,c>∈Ai×Ai ,又Ai×Ai ÍR∴有aRc
所以R传递。最后得R是集合X中的等价关系。
关于哈斯图的画法:
1.元素y盖住元素x:如果x≤y,且x≠y,且不存在z∈A,使
得z≠x∧z≠y∧x≤z∧z≤y,则称元素y盖住元素x。
元素y盖住xÛ x≤y∧x≠y∧Ø$z(z∈A∧z≠x∧z≠y∧x≤z∧ z≤y)
即元素y盖住元素xÛ不存在z∈A,使得z介于x与y之间。
上例中4没有盖住1,因为中间有个2, 1≤2≤4.
2.偏序集Hasse图的画法: 令<A,≤>是偏序集,
1).用“o”表示A中元素。
2).如果x≤y,且x≠y,则结点y要画在结点x的上方。
3). 如果x≤y,且y盖住x,x与y之间连一直线。
4). 一般先从最下层结点(全是射出的边与之相连(不考虑环)),逐层向上画,直到最上层结点(全是射入的边与之相连)。(采用抓两头,带中间的方法 )
y是B的极小元Û$y(y∈B∧Ø$x(x∈B∧x≠y∧x≤y)) ,(在B中没有比y更小的元素了,y就是极小元)
y是B的极大元Û$y(y∈B∧Ø$x(x∈B∧x≠y∧y≤x)) ,(在B中没有比y更大的元素了,y就是极大元)
y是B的最小元Û$y(y∈B∧"x(x∈B® y≤x)) ,(最小元y是B中元素,该元素比B中所有元素都小)
y是B的最大元Û$y(y∈B∧"x(x∈B® x≤y)) , (最大元y是B中元素,该元素比B中所有元素都大)
⑴B的极小(大)元总是存在的,就是子集中处在最下(上)层的元素是极小(大)元。
⑵B的最小元(最大元)有时可能不存在,只有有唯一的极小(大)元,则这个极小(大)元就是最小(大)元。否则就没有最小(大)元。
所有良序集,一定是全序集。有限的全序集,一定是良序集。
