必修一函数知识点总结
函数概念(一)知识梳理
1.映射的概念
设A、B是两个集合,如果按照某种对应法则f,对于集合A中的任意元素,在集合B中都有唯一确定的元素与之对应,那么这样的单值对应叫做从A到B的映射,通常记为f:A?B ,f表示对应法则
注意:⑴A中元素必须都有象且唯一;⑵B中元素不一定都有原象,但原象不一定唯一。
2.函数的概念
(1)函数的定义:
设A、B是两个非空的数集,如果按照某种对应法则f,对于集合A中的每一个数x,在集合B中都有唯一确定的数和它对应,那么这样的对应叫做从A到B的一个函数,通常记为y?f(x),x?A
(2)函数的定义域、值域
在函数y?f(x),x?A中,x叫做自变量,x的取值范围A叫做y?f(x)的定义域;与x的值相对应的y值叫做函数值,函数值的集合f(x)x?A称为函数y?f(x)的值域。
(3)函数的三要素:定义域、值域和对应法则
3.函数的三种表示法:图象法、列表法、解析法
(1).图象法:就是用函数图象表示两个变量之间的关系;
(2).列表法:就是列出表格来表示两个变量的函数关系;
(3).解析法:就是把两个变量的函数关系,用等式来表示。
4.分段函数
在自变量的不同变化范围中,对应法则用不同式子来表示的函数称为分段函数。
??
(二)考点分析
考点1:映射的概念
例1.(1)A?R,B?{y|y?0},f:x?y?|x|;
(2)A?{x|x?2,x?N},B??y|y?0,y?N?,f:x?y?x?2x?2; *2
(3)A?{x|x?0},B?{y|y?
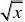
R},f:x?y?
上述三个对应 是A到B的映射.
例2.若A?{1,2,3,4},B?{a,b,c},a,b,c?R,则A到B的映射有 个,B到A的映射有 个,A到B的函数有 个
例3.设集合M?{?1,0,1},N?{?2,?1,0,1,2},如果从M到N的映射f满足条件:对M中的每个元素x与它在N中的象f(x)的和都为奇数,则映射f的个数是( )
(A)8个 (B)12个 (C)16个 (D)18个
考点2:判断两函数是否为同一个函数
例1. 试判断以下各组函数是否表示同一函数?
1
(1)f(x)?x2,g(x)?x3;
x?1(2)f(x)?,g(x)??x??1x?0, x?0;
*(3)f(x)?2nx2n?1,g(x)?(2nx)2n?1(n∈N);
(4)f(x)?xx?1,g(x)?x2?x;
(5)f(x)?x2?2x?1,g(t)?t2?2t?1
考点3:求函数解析式
方法总结:(1)若已知函数的类型(如一次函数、二次函数),则用待定系数法;
(2)若已知复合函数f[g(x)]的解析式,则可用换元法或配凑法;
(3)若已知抽象函数的表达式,则常用解方程组消参的方法求出f(x)
题型1:由复合函数的解析式求原来函数的解析式
例1.已知二次函数f(x)满足f(2x?1)?4x2?6x?5,求f(x)(三种方法)
1?x1?x2
)=例2.(09湖北改编)已知f(,则f(x)的解析式可取为 21?x1?x
题型2:求抽象函数解析式
例1.已知函数f(x)满足f(x)?2f()?3x,求f(x)
考点4:求函数的定义域
题型1:求有解析式的函数的定义域
(1)方法总结:如没有标明定义域,则认为定义域为使得函数解析式有意义的x的取值范围,实际操作时要注意:① 分母不能为0;② 对数的真数必须为正;③ 偶次根式中被开方数应为非负数;④ 零指数幂中,底数不等于0;⑤ 负分数指数幂中,底数应大于0;⑥ 若解析式由几个部分组成,则定义域为各个部分相应集合的交集;⑦ 如果涉及实际问题,还应使得实际问题有意义,而且注意:研究函数的有关问题一定要注意定义域优先原则,实际问题的定义域不要漏写。
例1.(08年湖北)函数f(x)?1x1ln(x2?3x?2??x2?3x?4)的定义域为( ) x
A.(??,?4)?[2,??);B.(?4,0)?(0,1);C. [,?4,0)?(0,1];D. [,?4,0)?(0,1)
题型2:求复合函数和抽象函数的定义域
例1.(2007·湖北)设f?x??lg2?xx??2?,则f????f??的定义域为( ) 2?x?2??x?
A. ??4,0???0,4?;B. ??4,?1???1,4?;C. ??2,?1???1,2?;D. ??4,?2???2,4?
例2.已知函数y?f(x)的定义域为[a,b],求y?f(x?2)的定义域
例3.已知y?f(x?2)的定义域是[a,b],求函数y?f(x)的定义域
例4.已知y?f(2x?1)的定义域是(-2,0),求y?f(2x?1)的定义域
考点5:求函数的值域
1. 求值域的几种常用方法
(1)配方法:对于(可化为)“二次函数型”的函数常用配方法,
2
如求函数y??sin2x?2cosx?4,可变为y??sin2x?2cosx?4?(cosx?1)2?2解决
(2)基本函数法:一些由基本函数复合而成的函数可以利用基本函数的值域来求, 如函数y?log1(?x?2x?3)就是利用函数y?log1u和u??x2?2x?3的值域来求。
222
(3)判别式法:通过对二次方程的实根的判别求值域。 如求函数y?2x?13?3?的值域[,] 2x?2x?222
2cosx?3的值域,因为 cosx?1(4)分离常数法:常用来求“分式型”函数的值域。 如求函数y?
(5)利用基本不等式求值域: 如求函数y?3x的值域 2x?4
(6)利用函数的单调性求求值域: 如求函数y?2x4?x2?2(x?[?1,2])的值域
(7)图象法:如果函数的图象比较容易作出,则可根据图象直观地得出函数的值域
(8)导数法――一般适用于高次多项式函数,如求函数f(x)?2x?4x?40x,x?[?3,3]的最小值。(-48) 32
m,(m>0)的函数,m<0就是单调函数了 x
4三种模型:(1)如y?x?,求(1)单调区间(2)x的范围[3,5],求值域(3)x ? [-1,0 )?(0,4],求值域 x(9)对勾函数法 像y=x+
(2)如 y?x?4求(1)[3,7]上的值域 (2)单调递增区间(x?0或x?4) x?4,
(3)如 y?2x?
1 , (1)求[-1,1]上的值域 (2)求单调递增区间 x?3
函数的单调性
(一)知识梳理
1、函数的单调性定义:
设函数y?f(x)的定义域为A,区间I?A,如果对于区间I内的任意两个值x1,x2,当x1?x2时,都有f(x1)?f(x2),那么就说y?f(x)在区间I上是单调增函数,I称为y?f(x)的单调增区间;如果对于区间I内的任意两个值x1,x2,当x1?x2时,都有f(x1)?f(x2),那么就说y?f(x)在区间I上是单调减函数,I称为y?f(x)的单调减区间。
如果用导数的语言来,那就是:设函数y?f(x),如果在某区间I上f?(x)?0,那么f(x)为区间I上的增函数;如果在某区间I上f?(x)?0,那么f(x)为区间I上的减函数;
2、确定函数的单调性或单调区间的常用方法:
(1)①定义法(取值――作差――变形――定号);②导数法(在区间(a,b)内,若总有f?(x)?0,则f(x)为增函数;反之,若f(x)在区间(a,b)内为增函数,则f?(x)?0,
b(a?0,b?0)型函数的图象和
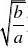
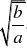
x
??
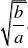
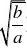
),减区间为[. 单调性在解题中的运用:增区间为(??,(2)在选择填空题中还可用数形结合法、特殊值法等等,特别要注意y?ax?
(3)复合函数法:复合函数单调性的特点是同增异减
3
(4)若f(x)与g(x)在定义域内都是增函数(减函数),那么f(x)?g(x)在其公共定义域内是增函数(减函数)。
3、单调性的说明:
(1)函数的单调性只能在函数的定义域内来讨论,所以求函数的单调区间,必须先求函数的定义域;
(2)函数单调性定义中的x1,x2有三个特征:一是任意性;二是大小,即x1?x2(x1?x2);三是同属于一个单调区间,三者缺一不可;
1分别在(??,0)和(0,??)内都是x
1单调递减的,但是不能说它在整个定义域即(??,0)?(0,??)内是单调递减的,只能说函数y?的单调递减区间为x(3)函数的单调性是对某个区间而言的,所以受到区间的限制,如函数y?
(??,0)和(0,??)。
4、函数的最大(小)值
设函数y?f(x)的定义域为A,如果存在定值x0?A,使得对于任意x?A,有f(x)?f(x0)恒成立,那么称f(x0)为y?f(x)的最大值;如果存在定值x0?A,使得对于任意x?A,有f(x)?f(x0)恒成立,那么称f(x0)为y?f(x)的最小值。
(二)考点分析
考点1 函数的单调性
题型1:讨论函数的单调性
例1.(1)求函数y?log0.7(x2?3x?2)的单调区间;
(2)已知f(x)?8?2x?x,若g(x)?f(2?x)试确定g(x)的单调区间和单调性.
例2. 判断函数f(x)=x?1在定义域上的单调性. 222
题型2:研究抽象函数的单调性
例1.已知函数f(x)的定义域是x?0的一切实数,对定义域内的任意x1,x2都有f(x1?x2)?f(x1)?f(x2),且当x?1时f(x)?0,f(2)?1,
2(1)求证:f(x)是偶函数;(2)f(x)在(0,??)上是增函数;(3)解不等式f(2x?1)?2.
题型3:函数的单调性的应用
例1.若函数f(x)?x?2(a?1)x?2 在区间(-∞,4] 上是减函数,那么实数a的取值范围是______ 例2.已知函数f(x)?2ax?1在区间??2,???上为增函数,则实数a的取值范围_____ x?2
考点2 函数的值域(最值)的求法
求最值的方法:(1)若函数是二次函数或可化为二次函数型的函数,常用配方法。(2)利用函数的单调性求最值:先判断函数在给定区间上的单调性,然后利用函数的单调性求最值。(3)基本不等式法:当函数是分式形式且分子分母不同次时常用此法(但有注意等号是否取得)。(4)导数法:当函数比较复杂时,一般采用此法(5)数形结合法:画出函数图象,找出坐标的范围或分析条件的几何意义,在图上找其变化范围。
题型1:求分式函数的最值
x2?2x?a1,x?[1,??).当a?时,求函数f(x)的最小值。 例1.(2007上海)已知函数f(x)?2x
题型2:利用函数的最值求参数的取值范围
4
x2?2x?a例2.(2008广东)已知函数f(x)?,x?[1,??).若对任意x?[1,??),f(x)?0恒成立,试求实数a的取x
值范围。
函数的奇偶性
(一)知识梳理
1、函数的奇偶性的定义:①对于函数f(x)的定义域内任意一个x,都有f(?x)??f(x)〔或
,则称f(x)为奇函数. f(x)的定义域内任意一个x,f(?x)?f(x)?0〕
都有f(?x)?f(x)〔或f(?x)?f(x)?0〕,则称f(x)为偶函数. 偶函数的图象关于y轴对称。
③通常采用图像或定义判断函数的奇偶性. 具有奇偶性的函数,其定义域关于原点对称(也就是说,函数为奇函数或偶函数的必要条件是其定义域关于原点对称)
2.函数的奇偶性的判断:
(1)可以利用奇偶函数的定义判断f(x)??f(?x)
(2)利用定义的等价形式, f(x)?f(?x)?0,f(?x)??1(f(x)?0) f(x)
(3)图像法:奇函数的图象关于原点对称;偶函数的图象关于y轴对称
3.函数奇偶性的性质:
(1)奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.
(2)若奇函数f(x)定义域中含有0,则必有f(0)?0.
证明:
(3)定义在关于原点对称区间上的任意一个函数,都可表示成“一个奇函数与一个偶函数的和(或差)”。如设f(x)是定义域为R的任一函数, F(x)?f(x)?f(?x)f(x)?f(?x),G(x)?。 22
(4)复合函数的奇偶性特点是:“内偶则偶,内奇同外”.
(5)设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:奇+奇=奇,奇?奇=偶,偶+偶=偶,偶?偶=偶,奇?偶=奇.
(6)定义域关于原点对称是奇偶函数的前提,因此,判断奇偶性必须先看定义域是否是关于原点对称的数集。
(7)既奇又偶的函数是存在的,而且不止一个;其解析式一定可以化为f?x??0,但是定义域可以不同。 证明:
(二)考点分析
考点1 判断函数的奇偶性及其应用
题型1:判断有解析式的函数的奇偶性
例1. 判断下列函数的奇偶性:
(1)f(x)=|x+1|-|x-1|;(2)f(x)=(x-1)·
?x; 1?x
?x(1?x)?x2
(3)f(x)?;(4)f(x)??|x?2|?2?x(1?x)
(x?0), (x?0).5
题型2:证明抽象函数的奇偶性
例1 .(09年山东)定义在区间(?1,1)上的函数f (x)满足:对任意的x,y?(?1,1),都有f(x)?f(y)?f(
证f (x)为奇函数;
例2.(1)函数f(x),x?R,若对于任意实数a,b,都有f(a?b)?f(a)?f(b),求证:f(x)为奇函数。
(2)设函数f(x)定义在(?l,l)上,证明f(x)?f(?x)是偶函数,f(x)?f(?x)是奇函数。
考点2 函数奇偶性、单调性的综合应用
例1.已知奇函数f(x)是定义在(?2,2)上的减函数,若f(m?1)?f(2m?1)?0,求实数m的取值范围。
例2.设函数f(x)对于任意的x,y?R,都有f(x?y)?f(x)?f(y),且x?0时f(x)?0,f(1)??2
(1)求证f(x)是奇函数;
(2)试问当?3?x?3时,f(x)是否有最值?如果有,求出最值;如果没有,说出理由。
22例3.设函数f(x)是定义在R上的偶函数,并在区间(-∞,0)内单调递增,f(2a+a+1)<f(3a-2a+1).求a的取值范
围,并在该范围内求函数y=(
x?y). 求1?xy1a2?3a?1)的单调递减区间. 2
2.5 二次函数
(一)知识梳理
1.二次函数的解析式的三种形式:
(1)一般式:f(x)=ax2+bx+c(a≠0)。
(2)顶点式(配方式):f(x)=a(x-h)2+k其中(h,k)是抛物线的顶点坐标。
(3)两点式(因式分解):f(x)=a(x-x1)(x-x2),其中x1,x2是抛物线与x轴两交点的坐标。
?bb4ac?b2
,) 2.二次函数f(x)=ax+bx+c(a≠0)的图象是一条抛物线,对称轴x?,顶点坐标(?2a2a4a2
(1)a>0时,抛物线开口向上,函数在(??,??bbb]上单调递减,在[?,??)上单调递增,x?时,2a2a2a
f(x)min
4ac?b2?; 4a6
(2)a<0时,抛物线开口向下,函数在(??,??bbb]上单调递增,在[?,??)上单调递减,x?时,2a2a2a
f(x)max4ac?b2?。 4a
23.二次函数f(x)=ax2+bx+c(a≠0)当??b?4ac?0时图象与x轴有两个交点M1(x1,0),M2(x2,0)
M1M2?x1?x2?(x1?x2)2?4x1x2?
2?。 a4. 最值问题:二次函数f(x)=ax+bx+c在区间[α,?]上的最值一般分为三种情况讨论,即:(1)对称轴?b/(2a)在区
间左边,函数在此区间上具有单调性;;(2)对称轴?b/(2a)在区间之内;(3)a的符号对二次函数、一元二次方程及一元二次不等式之间的关系:
222①??0?f(x)=ax+bx+c的图像与x轴无交点?ax+bx+c=0无实根?ax+bx+c>0(<0)的解集为?或者是R;
222②??0?f(x)=ax+bx+c的图像与x轴相切?ax+bx+c=0有两个相等的实根?ax+bx+c>0(<0)的解集为?或者是
R;
222③??0?f(x)=ax+bx+c的图像与x轴有两个不同的交点?ax+bx+c=0有两个不等的实根?ax+bx+c>0(<0)的解
集为(?,?)(???)或者是(??,?)?(?,??)
(二)考点分析
考点1.求二次函数的解析式
例1.已知二次函数f(x)满足f(2)= -1,f(-1)= -1且f(x)的最大值是8,试确定此二次函数。
法一:利用一般式
??a??4?4a?2b?c??1??22设f(x)=ax+bx+c(a≠0),由题意得:?a?b?c??1解得:?b?4 ∴f(x)= - 4x+4x+7
2?c?7?4ac?b?8??4a?
法二:利用顶点式
∵f(2)= f(-1) ∴对称轴x?2?(?1)1? 又最大值是8 22
∴可设f(x)?a(x?)?8(a?0),由f(2)= -1可得a= - 4 ?f(x)??4(x?)?8??4x?4x?7 法三:由已知f(x)+1=0的两根为x1=2,x2=-1,故可设f(x)+1=a(x-2)(x+1)即f(x)=ax-ax-2a-1,又21221222
ymax4a(?2a?1)?a2?8即?8得a= - 4或a=0(舍) ∴f(x)= - 4x2+4x+7 4a
例2
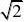
.已知二次函数的对称轴为x?x轴上的弦长为4,且过点(0,?1),求函数的解析式.
解:
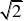
∵二次函数的对称轴为x?
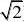
设所求函数为f(x)?a(x2?b,又∵f(x)截x轴上的弦长为4,∴f(x
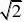
)过点(2,0),f(x)又过点(0,?1),
1??4a?b?0?a?∴?, ?2,
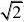
2a?b??1???b??2
∴f(x)?1(x2?2 2
7 考点2.二次函数在区间上的最值问题
例1.已知函数f(x)= - x+2ax+1-a在0≤x≤1时有最大值2,求a的值。
2例2.已知y=f(x)=x-2x+3,当x∈[-1,3]时,求函数的最大值和最小值。
考点3.一元二次方程根的分布及取值范围
2例1.已知关于x的二次方程x+2mx+2m+1=0
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的取值范围。
(2)若方程两根在区间(0,1)内,求m的范围。
思维分析:一般需从三个方面考虑①判别式Δ②区间端点函数值的正负③对称轴x??2b与区间相对位置。 2a
【反思归纳】根分布问题: 一般地对于含有字母的一元二次方程ax2+bx+c=0 的实根分布问题,用图象求解,主要研究开口、判别式、对称轴、区间端点对应函数值的正负,列出不等式(组)求解。
例2. 已知函数f(x)?x?(2a?1)x?a?2与x轴至少有一个交点,求a的取值范围.
22
指数与指数函数
(一)知识梳理
1.指数运算
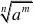
a?m
n;a?m
?ma;a0?1;ar?as?ar?s(a?0,r、s?Q);(ar)s?ars(a?0,r、s?Q);
(ab)r?arbs(a?0,r、s?Q)
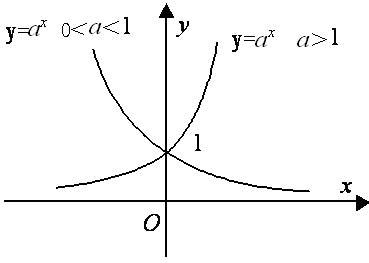
2.指数函数:y?ax(a?0,a?1),定义域R,值域为(0,??).⑴
①当a?1,指数函数:y?ax在定义域上为增函数;②当0?a?1,
指数函数:y?ax在定义域上为减函数.⑵当a?1时,y?ax的a值越
大,越靠近y轴;当0?a?1时,则相反.
8
(二)考点分析
mnmn例1.已知下列不等式,比较m,n的大小:(1)2?2 (2)0.2?0.2
变式1:设
a111?()b?()a?1,那么 ( ) 222baaabA.a<a<b B.a< b<a
C.a<a<b D.a<b<a
例2.函数y?a在[0,1]上的最大值与最小值的和为3,则a的值为( ) xbaabaa
11 B.2 C.4 D. 24
x例3.已知函数y?f(x)的图象与函数y?a(a?0且a?1)的图象关于直线y?x对称,记
1g(x)?f(x)[f(x)?2f(2)?1].若y?g(x)在区间[,2]上是增函数,则实数a的取值范围是( ) 2
11 A.[2,??) B.(0,1)?(1,2) C.[,1) D.(0,] 22A.
对数与对数函数
(一)知识梳理
1.对数运算:
loga(M?N)?logaM?logaN;loga
logaN?alogaN?N;换底公式:1M?logaM?logaN;logaMn?
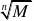
nlogaM;loga?logaM;nNlogbN;推论:logab?logbc?logca?1 logba
2.对数函数:如果a(a?0,a?1)的b次幂等于N,就是ab?N,数b就叫做以a为底的N的对数,记作logaN?b(a?0,a?1,负数和零没有对数);其中a叫底数,N叫真数.
当a?1时,y?logax的a值越大,越靠近x轴;当0?a?1时,则相反.
(二)考点分析
例1.已知函数f(x)?loga(x?1),g(x)?loga(1?x)(a?0,且a?1)
(1) 求函数f(x)?g(x)定义域
(2) 判断函数f(x)?g(x)的奇偶性,并说明理由.
例2.已知f(x)??
A.(0,1) 例3.若loga?(3a?1)x?4a,x?1是(??,??)上的减函数,那么a的取值范围是 ?logax,x?1131173 D.[,1) B.(0,) C.[,) 173?1(a?0,且a?1),求实数a的取值范围. 4
D.(0,) 1?a211?0,则a的取值范围是 ( ) A.(,??) B.(1,??) C.(,1) 变式1:若log2a221?a
129
幂函数
(一)知识梳理1、幂函数的概念
一般地,形如y?x? (x?R)的函数称为幂函数,其中x是自变量,?是常数
2、幂函数的图像及性质
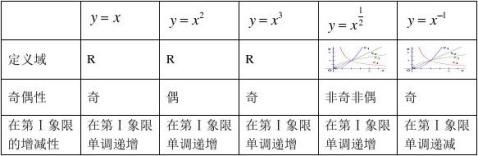
幂函数y?x? (x?R,?是常数)的图像在第一象限的分布规律是:
①所有幂函数y?x? (x?R,?是常数)的图像都过点(1,1);
②当??0时函数y
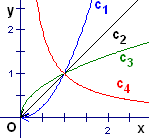
?x?的图像都过原点(0,0);
③当??1时,y?x?的的图像在第一象限是第一象限的平分线(如c2);
④当??2,3时,y?x?的的图像在第一象限是“凹型”曲线(如c1)
⑤当??1
2时,y?x?的的图像在第一象限是“凸型”曲线(如c3)
⑥当???1时,y?x?的的图像不过原点(0,0),且在第一象限是“下滑”曲线(如c4)
3、重难点问题探析:幂函数性质的拓展
当??0时,幂函数y?x?有下列性质:
(1)图象都通过点(0,0),(1,1);
(2)在第一象限内都是增函数;
(3)在第一象限内,??1时,图象是向下凸的;1???0时,图象是向上凸的;
(4)在第一象限内,过点(1,1)后,图象向右上方无限伸展。
当0??时,幂函数y?x?有下列性质:
(1)图象都通过点(1,1);
(2)在第一象限内都是减函数,图象是向下凸的;
(3)在第一象限内,图象向上与y轴无限地接近;向右无限地与x轴无限地接近;
(4)在第一象限内,过点(1,1)后,?越大,图象下落的速度越快。
无论?取任何实数,幂函数y?x?的图象必然经过第一象限,并且一定不经过第四象限。 10
(二)考点分析
考点1:利用幂函数的单调性比较大小
?1?例1.已知??0,试比较??,0.2?,2?的大小; ?2?
1??例2
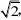
.已知点在幂函数f(x)的图象上,点??2?,在幂函数g(x)的图象上. 4??
问当x为何值时有:(1)f(x)?g(x);(2)f(x)?g(x);(3)f(x)?g(x). ?
函数图象
(一)知识梳理
1.函数图象
(1)作图方法:以解析式表示的函数作图象的方法有两种,即列表描点法和图象变换法,掌握这两种方法是本讲座的重点。
作函数图象的步骤:①确定函数的定义域;②化简函数的解析式;③讨论函数的性质即单调性、奇偶性、周期性、最值(甚至变化趋势);④描点连线,画出函数的图象。 运用描点法作图象应避免描点前的盲目性,也应避免盲目地连点成线要把表列在关键处,要把线连在恰当处就要求对所要画图象的存在范围、大致特征、变化趋势等作一个大概的研究。而这个研究要借助于函数性质、方程、不等式等理论和手段,是一个难点以及确定怎样的变换,这也是个难点
(2)三种图象变换:平移变换、对称变换和伸缩变换等等;
①平移变换: Ⅰ、水平平移:函数y?f(x?a)的图像可以把函数y?f(x)的图像沿x轴方向向左(a?0)或向右(a?0)平移|a|个单位即可得到;
左移h
1)y=f(x)?右移hy=f(x+h);2)y=f(x) ?y=f(x?h);
Ⅱ、竖直平移:函数y?f(x)?a的图像可以把函数y?f(x)的图像沿x轴方向向上(a?0)或向下(a?0)平移|a|个单位即可得到;
1)y=f(x) ?
②对称变换:
Ⅰ、函数y?f(?x)的图像可以将函数y?f(x)的图像关于y轴对称即可得到; 上移hy=f(x)+h;2)y=f(x) 下移h?y=f(x)?h。
y=f(x) ?y=f(?x) y轴
Ⅱ、函数y??f(x)的图像可以将函数y?f(x)的图像关于x轴对称即可得到;
y=f(x) ?y= ?f(x) x轴
Ⅲ、函数y??f(?x)的图像可以将函数y?f(x)的图像关于原点对称即可得到;
y=f(x) 原点?y= ?f(?x)
Ⅳ、函数x?f(y)的图像可以将函数y?f(x)的图像关于直线y?x对称得到。
11
y=f(x) 直线y?x?x=f(y)
Ⅴ、函数y?f(2a?x)的图像可以将函数y?f(x)的图像关于直线x?a对称即可得到;
y=f(x) 直线x?a?y=f(2a?x)。
③翻折变换:
Ⅰ、函数y?|f(x)|的图像可以将函数y?f(x)的图像的x轴下方部分沿x轴翻折到x轴上方,去掉原x轴下方部分,并保留y?f(x)的x轴上方部分即可得到;
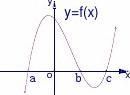
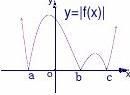
Ⅱ、函数y?f(|x|)的图像可以将函数y?f(x)的图像右边沿y轴翻折到y轴左边替代原y轴左边部分并保留y?f(x)在y
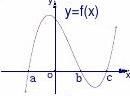
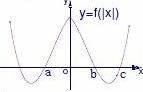
④伸缩变换:
Ⅰ、函数y?af(x)(a?0)的图像可以将函数y?f(x)的图像中的每一点横坐标不变纵坐标伸长(a?1)或压缩(0?a?1)为原来的a倍得到;
y=f(x)?y=af(x)
Ⅱ、函数y?f(ax)(a?0)的图像可以将函数y?f(x)的图像中的每一点纵坐标不变横坐标伸长(a?1)或压缩(0?a?1)为原来的y?a1倍得到。 a
f(x)=f(x)?y=f(ax) x?a
(3)识图:分布范围、变化趋势、对称性、周期性等等方面
(二)考点分析
例1.(08江苏理14)
3设函数f(x)?ax?3x?1(x?R),若对于任意的x???1,1?都有f(x)?0成立,则实数a的值为
点评:该题属于实际应用的题目,结合函数值变化的趋势和一些特殊点函数值解决问题即可。要明确函数图像与函数自变量、变量值的对应关系,特别是函数单调性与函数图象个关系;
题型3:函数的图象变换
|x|例9.已知0?a?1,方程a?|logax|的实根个数为( )A.2 B.3 C.4 D.2或3或4
点评:该题属于“数形结合”的题目。解题思路是将“函数的零点”问题转化为“函数的交点问题”,借助函数的图象以及函数的图象变换规则求得结果即可。
12
2.10 函数与方程
(一)知识梳理
1.函数零点
概念:对于函数y?f(x)(x?D),把使f(x)?0成立的实数x叫做函数y?f(x)(x?D)的零点。
函数零点的意义:函数y?f(x)的零点就是方程f(x)?0实数根,亦即函数y?f(x)的图象与x轴交点的横坐标。即:方程f(x)?0有实数根?函数y?f(x)的图象与x轴有交点?函数y?f(x)有零点。
零点存在性定理:如果函数y?f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)f(b)?0,那么函数y?f(x)在区间(a,b)内有零点。既存在c?(a,b),使得f(c)?0,这个c也就是方程的根。
2.二分法
二分法及步骤:
对于在区间[a,b]上连续不断,且满足f(a)·f(b)?0的函数y?f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
给定精度?,用二分法求函数f(x)的零点近似值的步骤如下:
(1)确定区间[a,b],验证f(a)·f(b)?0,给定精度?;
(2)求区间(a,b)的中点x1;
(3)计算f(x1):
①若f(x1)=0,则x1就是函数的零点;
②若f(a)·f(x1)<0,则令b=x1(此时零点x0?(a,x1));
③若f(x1)·f(b)<0,则令a=x1(此时零点x0?(x1,b));
(4)判断是否达到精度?;
即若|a?b|??,则得到零点零点值a(或b);否则重复步骤2~4。
(二)考点分析
题型1:方程的根与函数零点
例1.(1)方程lgx+x=3的解所在区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
(2)设a为常数,试讨论方程lg(x?1)?lg(3?x)?lg(a?x)的实根的个数。
点评:图象法求函数零点,考查学生的数形结合思想。本题是通过构造函数用数形结合法求方程lgx+x=3解所在的区间。数形结合,要在结合方面下功夫。不仅要通过图象直观估计,而且还要计算x0的邻近两个函数值,通过比较其大小进行判断
13
