导数的基础知识
一.导数的定义:
1.(1).函数y?f(x)在x?x0处的导数:f'(x0)?y'|x?x?lim
f(x0??x)?f(x0)
?x
?x?0
(2).函数y?f(x)的导数:f'(x)?y'?lim
?x?0
f(x??x)?f(x)
?x
?y?x
2.利用定义求导数的步骤:
①求函数的增量:?y?f(x0??x)?f(x0);②求平均变化率:③取极限得导数:f'(x0)?lim(下面内容必记)
?y?x
?
f(x0??x)?f(x0)
?x
;
?x?0
二、导数的运算:
(1)基本初等函数的导数公式及常用导数运算公式: ①C'?0(C为常数);②(x)'?nx
n
n?1
;(
1x
n
m
)'?(x
x
?n
)'??
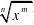
nx
x
?n?1
;'?(x)'?
x
n
mn
m
x
n
?1
③(sinx)'?cosx; ④(cosx)'??sinx ⑤(e)'?e ⑥(a)'?alna(a?0,且a?1); ⑦(lnx)'?
1
xxlna
法则1:[f(x)?g(x)]'?f'(x)?g'(x);(口诀:和与差的导数等于导数的和与差).
x
; ⑧(logax)'?
1
(a?0,且a?1)
法则2:[f(x)?g(x)]'?f'(x)?g(x)?f(x)?g'(x)(口诀:前导后不导相乘,后导前不导相乘,中间是正号) 法则3:[
f(x)g(x)
]'?
f'(x)?g(x)?f(x)?g'(x)
[g(x)]
2
(g(x)?0)
(口诀:分母平方要记牢,上导下不导相乘,下导上不导相乘,中间是负号) (2)复合函数y?f(g(x))的导数求法:
①换元,令u?g(x),则y?f(u)②分别求导再相乘y'??g(x)?'??f(u)?'③回代u?g(x) 题型一、导数定义的理解 题型二:导数运算 1、已知f
?x??
x
x?2x?sin?,则f
2'
?0??
2、若f?x??
10
esinx
,则f
13
'
?x??C.163
D.193
3.f(x)=ax3+3x2+2 ,f?(?1)?4,则a=( )
33
三.导数的物理意义 A.
B.
1.求瞬时速度:物体在时刻t0时的瞬时速度V0就是物体运动规律S?f?t?在t?t0 时的导数f??t0?, 即有V0?f??t0?。
//
2.V=s(t) 表示即时速度。a=v(t) 表示加速度。
四.导数的几何意义:
函数f?x?在x0处导数的几何意义,曲线y?f?x?在点P?x0,f?x0??处切线的斜率是k?f??x0?。于是相应的切线方程是:y?y0?f??x0??x?x0?。 题型三.用导数求曲线的切线 注意两种情况:
(1)曲线y?f?x?在点P?x0,f?x0??处切线:性质:k切线?f??x0?。相应的切线方程是:y?y0?f??x0??x?x0? (2)曲线y?f?x?过点P?x0,y0?处切线:先设切点,切点为Q(a,b) ,则斜率k=f'(a),切点Q(a,b) 在曲线y?f?x?上,切点Q(a,b)在切线y?y0?f??a??x?x0?上,切点Q(a,b)坐标代入方程得关于a,b的方程组,解方程组来确定切点,最后求斜率k=f'(a),确定切线方程。
例题在曲线y=x3+3x2+6x-10的切线中,求斜率最小的切线方程;
1
解析:(1)k?y'|x?x?3x02?6x0?6?3(x0?1)2?3当x0=-1时,k有最小值3,
此时P的坐标为(-1,-14)故所求切线的方程为3x-y-11=0 0
五.函数的单调性:设函数y?f(x)在某个区间内可导,
(1)f'(x)?0?f(x)该区间内为增函数;
(2)f'(x)?0?f(x)该区间内为减函数;
注意:当f'(x)在某个区间内个别点处为零,在其余点处为正(或负)时,f(x)在这个区间上仍是递增(或递减)的。
(3)f(x)在该区间内单调递增?f'(x)?0在该区间内恒成立;
(4)f(x)在该区间内单调递减?f'(x)?0在该区间内恒成立;
题型一、利用导数证明(或判断)函数f(x)在某一区间上单调性:
步骤: (1)求导数 y??f?(x)
(2)判断导函数y??f?(x)在区间上的符号
(3)下结论
①f'(x)?0?f(x)该区间内为增函数;
②f'(x)?0?f(x)该区间内为减函数;
题型二、利用导数求单调区间
求函数y?f(x)单调区间的步骤为:
(1)分析 y?f(x)的定义域; (2)求导数 y??f?(x)
(3)解不等式f?(x)?0,解集在定义域内的部分为增区间
(4)解不等式f?(x)?0,解集在定义域内的部分为减区间
题型三、利用单调性求参数的取值(转化为恒成立问题)
思路一.(1)f(x)在该区间内单调递增?f'(x)?0在该区间内恒成立;
(2)f(x)在该区间内单调递减?f'(x)?0在该区间内恒成立;
思路二.先求出函数在定义域上的单调增或减区间,则已知中限定的单调增或减区间是定义域上的单调增或减区间的子
集。
注意:若函数f(x)在(a,c)上为减函数,在(c,b)上为增函数,则x=c两侧使函数f?(x)变号,即x=c为函数的一个极值点,所以f'(c)?0 例题.若函数f(x)?lnx
x,若a?f(3),b?f(4),c?f(5)则( )
A. a< b < c B. c < b < a C. c < a < b D. b < a < c
六、函数的极值与其导数的关系:
1.①极值的定义:设函数f(x)在点x0附近有定义,且若对x0附近的所有的点都有f(x)?f(x0)(或f(x)?f(x0),则称f(x0)为函数的一个极大(或小)值,x0为极大(或极小)值点。
②可导数f(x)在极值点(即f'(x0)?0),但函数f(x)在某点x0处的导数为0,并不一定函数f(x)在...x0处的导数为0
3该处取得极值(如f(x)?x在x0?0处的导数为0,但f(x)没有极值)。
③求极值的步骤:
第一步:求导数f'(x);
第二步:求方程f'(x)?0的所有实根;
第三步:列表考察在每个根x0附近,从左到右,导数f'(x)的符号如何变化,
若f'(x)的符号由正变负,则f(x0)是极大值;
若f'(x)的符号由负变正,则f(x0)是极小值;
若f'(x)的符号不变,则f(x0)不是极值,x0不是极值点。
2、函数的最值:
①最值的定义:若函数在定义域D内存x0,使得对任意的x?D,都有f(x)?f(x0),(或f(x)?f(x0))则称f(x0)为函数的最大(小)值,记作ymax?f(x0)(或ymin?f(x0))
②如果函数y?f(x)在闭区间[a,b]上的图象是一条连续不间断的曲线,则该函数在闭区间[a,b]上必有最大值和最小值。
③求可导函数f(x)在闭区间[a,b]上的最值方法:
第一步;求f(x)在区间[a,b]内的极值;
第二步:比较f(x)的极值与f(a)、f(b)的大小:
第三步:下结论:最大的为最大值,最小的为最小值。
2
注意:1、极值与最值关系:函数的最值是比较整个定义域区间的函数值得出的,函数的最大值和最小值点可以在极值
点、不可导点、区间的端点处取得。极值≠最值。函数f(x)在区间[a,b]上的最大值为极大值和f(a) 、f(b)中最大的一个。最小值为极小值和f(a) 、f(b)中最小的一个。
2.函数在定义域上只有一个极值,则它对应一个最值(极大值对应最大值;极小值对应最小值)
3、注意:极大值不一定比极小值大。如f(x)?x?
//1x的极大值为?2,极小值为2。 注意:当x=x0时,函数有极值? f(x0)=0。但是,f(x0)=0不能得到当x=x0时,函数有极值;
判断极值,还需结合函数的单调性说明。
题型一、求极值与最值
题型二、导数的极值与最值的应用
题型四、导数图象与原函数图象关系
导函数 原函数
f'(x)的符号 f(x)单调性
f'(x)与x轴的交点且交点两侧异号 f(x)极值
f'(x)的增减性 f(x)的每一点的切线斜率的变化趋势 (f(x)的图象的增减幅度) f'(x)的增 f(x)的每一点的切线斜率增大(f(x)的图象的变化幅度快)
f'(x)减 f(x)的每一点的切线斜率减小 (f(x)的图象的变化幅度慢)
例1. 已知f(x)=e-ax-1.
(1)求f(x)的单调增区间;(2)若f(x)在定义域R内单调递增,求a的取值范围;
(3)是否存在a,使f(x)在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出a的值;若不存在,说明理由.
解:f?(x)x=e-a.(1)若a≤0,
xxxf?(x)=e-a≥0恒成立,即f(x)在R上递增. x若a>0,e-a≥0,∴e≥a,x≥lna.∴f(x)的单调递增区间为(lna,+∞).
(2)∵f(x)在R内单调递增,∴
xxf?(x)≥0在R上恒成立. xx∴e-a≥0,即a≤e在R上恒成立.∴a≤(e)min,又∵e>0,∴a≤0.
(3) 由题意知,x=0为f(x)的极小值点.∴
32f?(0)=0,即e-a=0,∴a=1. 2
30例2. 已知函数f(x)=x+ax+bx+c,曲线y=f(x)在点x=1处的切线为l:3x-y+1=0,若x=时,y=f(x)有极值.(1)求
a,b,c的值;(2)求y=f(x)在[-3,1]上的最大值和最小值.
解 (1)由f(x)=x+ax+bx+c,得32f?(x)=3x+2ax+b, 2
当x=1时,切线l的斜率为3,可得2a+b=0 ①
当x=时,y=f(x)有极值,则32?2?f???
?3?=0,可得4a+3b+4=0 ②
由①②解得a=2,b=-4.由于切点的横坐标为x=1,∴f(1)=4.∴1+a+b+c=4.∴c=5.
(2)由(1)可得f(x)=x+2x-4x+5,∴32f?(x)=3x+4x-4,令2f?(x)=0,得x=-2,x=. 32
当x变化时,y,y′的取值及变化如下表:
x -3 (-3,-2) +
单调递增
↗ -2 0 13 2????2,?3?? 23 ?2??,1??3? 1 4 y′ y 8 - 单调递减
↘ 0 9527+ 单调递增 ↗
95
27. ∴y=f(x)在[-3,1]上的最大值为13,最小值为
3
例3.当 x?0,证明不等式证明:f(x)?ln(x?1)?
x1?x
?ln(1?x)?x.
x(1?x)
2
x1?x
,g(x)?ln(x?1)?x,则f?(x)?,
x1?x
?0,
当x?0时。?f(x)在?0,???内是增函数,?f(x)?f(0),即ln(1?x)?又g?(x)?
?x1?x
,当x?0时,g?(x)?0,?g(x)在?0,???内是减函数,?g(x)?g(0),即ln(1?x)?x?0,因
x1?x
?ln(1?x)?x成立.
x1?x
此,当x?0时,不等式
点评:由题意构造出两个函数f(x)?ln(x?1)?,g(x)?ln(x?1)?x.
利用导数求函数的单调区间或求最值,从而导出是解决本题的关键.
七定积分求值
1.定积分的概念 设函数f(x)在区间[a,b]上连续,则?f(x)dx?lim
ab
n
n??
?f???
i
i?1
b?an
n
n等分区间?a,b?;2.用定义求定积分的一般方法是:①分割:②近似代替:取点?i??xi?1,xi?;③求和:?
i?1
b?an
f(?i);
④取极限:?f(x)dx?lim
a
b
n
n??
?
i?1
f??i?
b?an
0,S???
ba
3.曲边图形面积:f?x??0,S?
t2t1
?
ba
f
?x?dx;f?x??
f
?x?dx
在x轴上方的面积取正,下方的面积取负 变速运动路程S?
4.定积分的性质
性质1 ?kf(x)dx?k?f(x)dx (其中k是不为0的常数)
a
a
b
b
?
v(t)dt; 变力做功 W?
?
ba
F(r)dr
性质2 ?[f1(x)?f2(x)]dx?
ab
c
b
?
bab
f1(x)dx?
?
ba
f2(x)dx
性质3 ?f(x)dx?
a
?
a
f(x)dx?
?
c
f(x)dx(其中a?c?b) (定积分对积分区间的可加性)
b
b
5.定理 函数F(x)是[a,b]上f(x)的一个原函数,即f(x)?F?(x)则?f(x)dx?F(x)|a?F(b)?F(a)
a
导数各种题型方法总结
(一)关于二次函数的不等式恒成立的主要解法:
1、分离变量;2变更主元;3根分布;4判别式法5、二次函数区间最值求法: (1)对称轴(重视单调区间)与定义域的关系 (2)端点处和顶点是最值所在
(二)分析每种题型的本质,你会发现大部分都在解决“不等式恒成立问题”以及“充分应用数形结合思想”,创建不等关系求出取值范围。
(三)同学们在看例题时,请注意寻找关键的等价变形和回归的基础
一、基础题型:函数的单调区间、极值、最值;不等式恒成立;
1、此类问题提倡按以下三个步骤进行解决:
第一步:令f(x)?0得到两个根; 第二步:画两图或列表; 第三步:由图表可知;
'
其中不等式恒成立问题的实质是函数的最值问题,
4
2、常见处理方法有三种:
第一种:分离变量求最值-----用分离变量时要特别注意是否需分类讨论(>0,=0,<0) 第二种:变更主元(即关于某字母的一次函数)-----(已知谁的范围就把谁作为主元);
例1:设函数y?f(x)在区间D上的导数为f?(x),f?(x)在区间D上的导数为g(x),若在区间D上,g(x)?0恒
2
成立,则称函数y?f(x)在区间D上为“凸函数”,已知实数m是常数,f(x)?x433x
12?mx
6?2
(1)若y?f(x)在区间?0,3?上为“凸函数”,求m的取值范围;
(2)若对满足m?2的任何一个实数m,函数f(x)在区间?a,b?上都为“凸函数”,求b?a的最大值. 解:由函数f(x)?x4mx322
12?6?3x
2 得f?(x)?x3mx
3?2?3x
?g(x)?x2?mx?3
(1) ?y?f(x)在区间?0,3?上为“凸函数”,
则 ?g(x)?x2?mx?3?0 在区间[0,3]上恒成立
解法一:从二次函数的区间最值入手:等价于gmax(x)?0
?g(0)?0
?0????30
?g(3)??m3??3?0m?2
??9
解法二:分离变量法:
∵ 当x?0时, ?g(x)?x2?mx?3??3?0恒成立,
当0?x?3时, g(x)?x2?mx?3?0恒成立
2
等价于m?x?3
x?x?3
x的最大值(0?x?3)恒成立,
而h(x)?x?3
x(0?x?3)是增函数,则hmax(x)?h(3)?2
?m?2
(2)∵当m?2时f(x)在区间?a,b?上都为“凸函数”
则等价于当m?2时g(x)?x2?mx?3?0 恒成立
变更主元法
再等价于F(m)?mx?x2?3?0在m?2恒成立(视为关于m的一次函数最值问题)
2
??F(?2)?0??x2?x??3
???0
?F(2)?0???1?x?1
??2x?x2?3?0
?b?a?2
例2:设函数f(x)??132
3x?2ax2?3ax?b(0?a?1,b?R)
(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若对任意的x?[a?1,a?2],不等式f?(x)?a恒成立,求a的取值范围. (二次函数区间最值的例子)
解:(Ⅰ)f?(x)??x2?4ax?3a2???x?3a??x?a?
?0?a?1
5
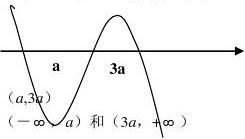
3
4 ∴当x=a时,f(x)极小值=?a3?b; 当x=3a时,f(x)极大值=b.
22 (Ⅱ)由|f?(x)|≤a,得:对任意的x?[a?1,a?2],?a?x?4ax?3a?a恒成立①
则等价于g(x)这个二次函数??gmax(x)?a g(x)?x?4ax?3a的对称轴x?2a ?0?a?1, 22
?gmin(x)??a
a?1?a?a?2a(放缩法)
即定义域在对称轴的右边,g(x)这个二次函数的最值问题:单调增函数的最值问题。
g(x)?x2?4ax?3a2在[a?1,a?2]上是增函数.
∴g(x)max?g(a?2)??2a?1.
g(x)min?g(a?1)??4a?4.
于是,对任意x?[a?1,a?2],不等式①恒成立,等价于
?1,a?2? ?g(a?2)??4a?4?a,
x?a??g(a?1)??2a?1??a解得4
5?a?1.
又0?a?1,∴4
5?a?1.
点评:重视二次函数区间最值求法:对称轴(重视单调区间)与定义域的关系
第三种:构造函数求最值
题型特征:f(x)?g(x)恒成立?h(x)?f(x)?g(x)?0恒成立;从而转化为第一、二种题型
例3;已知函数f(x)?x3?ax2图象上一点P(1,b)处的切线斜率为?3,
g(x)?x3?t?62
2x?(t?1)x?3(t?0)
(Ⅰ)求a,b的值;
(Ⅱ)当x?[?1,4]时,求f(x)的值域;
(Ⅲ)当x?[1,4]时,不等式f(x)?g(x)恒成立,求实数t的取值范围。
解:(Ⅰ)f/(x)?3x2?2ax∴?f/(1)??3?, 解得?a??3
a?
?b?1??b??2
(Ⅱ)由(Ⅰ)知,f(x)在[?1,0]上单调递增,在[0,2]上单调递减,在[2,4]上单调递减
又f(?1)??4,f(0)?0,f(2)??4,f(4)?16
∴f(x)的值域是[?4,16]
(Ⅲ)令h(x)?f(x)?g(x)??t2
2x?(t?1)x?3x?[1,4]
思路1:要使f(x)?g(x)恒成立,只需h(x)?0,即t(x2?2x)?2x?6分离变量
思路2:二次函数区间最值
二、已知函数在某个区间上的单调性求参数的范围
解法1:转化为f'(x)?0或f'(x)?0在给定区间上恒成立, 回归基础题型
解法2:利用子区间(即子集思想);首先求出函数的单调增或减区间,然后让所给区间是求的增或减区间的子集;
6 9(
做题时一定要看清楚“在(m,n)上是减函数”与“函数的单调减区间是(a,b)”,要弄清楚两句话的区别:前者是后者的子集
例4:已知a?R,函数f(x)?1
12x?3a?1
2x2?(4a?1)x.
(Ⅰ)如果函数g(x)?f?(x)是偶函数,求f(x)的极大值和极小值;
(Ⅱ)如果函数f(x)是(??,
解:f?(x)???)上的单调函数,求a的取值范围. 1
4x2?(a?1)x?(4a?1).
1
123x?3x,f?(x)? (Ⅰ)∵ f?(x)是偶函数,∴ a??1. 此时f(x)? 令f?(x)?0,解得:x??2
14x2?3, 3.

(Ⅱ)∵函数f(x)是(??,
∴f?(x)? ??)上的单调函数, 1
4x?(a?1)x?(4a?1)?0,在给定区间2
2R上恒成立判别式法 则??(a?1)?4?1
4?(4a?1)?a?2a?0, 解得:0?a?2. 2
综上,a的取值范围是{a0?a?2}.
例5、已知函数f(x)?1
3x?31
2(2?a)x?(1?a)x(a?0). 2
(I)求f(x)的单调区间;
(II)若f(x)在[0,1]上单调递增,求a的取值范围。子集思想
2(I)f?(x)?x?(2?a)x?1?a?(x?1)(x?1?a).
2 1、当a?0时,f?(x)?(x?
1)?0恒成立,
当且仅当x??1时取“=”号,f(x)在(??,??)单调递增。
2、当a?0时,由f?(x)?0,得x1??1,x2?a?1,且x1?x2,
单调增区间:(??,?1),(a?1,??)
单调增区间:(?1,a?1) (II)当?f(x)在[0,1]上单调递增, 则?0,1?是上述增区间的子集: 1、a?0时,f(x)在(??,??)单调递增 符合题意
2、?0,1???a?1,???,?a?1?0 ?a?1
综上,a的取值范围是[0,1]。
三、根的个数问题
提型一 函数f(x)与g(x)(或与x轴)的交点======即方程根的个数问题
解题步骤
第一步:画出两个图像即“穿线图”(即解导数不等式)和“趋势图”即三次函数的大致趋势“是先增后减再增”还是“先减后增再减”;
第二步:由趋势图结合交点个数或根的个数写不等式(组);主要看极大值和极小值与0的关系; 7
第三步:解不等式(组)即可;
例6、已知函数f(x)?
13x
3
?
(k?1)2
x,g(x)?
2
13
?kx,且f(x)在区间(2,??)上为增函数.
(1) 求实数k的取值范围;
(2) 若函数f(x)与g(x)的图象有三个不同的交点,求实数k的取值范围.
2
解:(1)由题意f?(x)?x?(k?1)x ∵f(x)在区间(2,??)上为增函数,
2
∴f?(x)?x?(k?1)x?0在区间(2,??)上恒成立(分离变量法)
即k?1?x恒成立,又x?2,∴k?1?2,故k?1∴k的取值范围为k?1 (2)设h(x)?f(x)?g(x)?
h?(x)?x
2
x
3
3
?
(k?1)2
x
2
?kx?
13
,
?(k?1)x?k?(x?k)(x?1)
2
令h?(x)?0得x?k或x?1由(1)知k?1,
①当k?1时,h?(x)?(x?1)?0,h(x)在R上递增,显然不合题意? ②当k?1时,h(x),h?(x)随x的变化情况如下表:
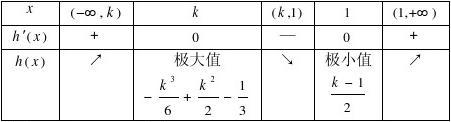
由于
?k
3
k?12
2
?0,欲使f(x)与g(x)的图象有三个不同的交点,即方程h(x)?0有三个不同的实根,故需
6
?
k
2
?
13
?0,即(k?1)(k
2
?k?1
?2k?2)?0 ∴?2,解得k?1?
k?2k?2?0?
3
综上,所求k的取值范围为k?1?3
根的个数知道,部分根可求或已知。 例7、已知函数f(x)?ax?
3
12
x?2x?c
2
(1)若x??1是f(x)的极值点且f(x)的图像过原点,求f(x)的极值; (2)若g(x)?
12
bx?x?d,在(1)的条件下,是否存在实数b,使得函数g(x)的图像与函数f(x)的图像恒有含
高考资源网
2
x??1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由。
解:(1)∵2
f(x)的图像过原点,则f(0)?0?c?0 f?(x)?3ax?x?2,
又∵x??1是f(x)的极值点,则f?(?1)?3a?1?2?0?a??1
2
?f?(x)?3x?x?2?(3x?2)(x?1)?0
222?)?
237
(2)设函数g(x)的图像与函数
f(x)的图像恒存在含x??1的三个不同交点, f极大值(x)?f(?1)?
3
f极小值(x)?f
等价于f(x)?g(x)有含x??1的三个根,即:f(?1)?g(?1)?d??
?x?
3
12
(b?1)
12
x?2x?
2
12
bx?x?
2
12
(b?1)整理得:
即:x?
3
12
(b?1)x?x?
2
12
(b?1)?0恒有含x??1的三个不等实根 x?
3
(计算难点来了:)h(x)?
12
(b?1)x?x?
2
12
(b?1)?0有含x??1的根,
8
则h(x)必可分解为(x?1)(二次式)?0,故用添项配凑法因式分解,
x?x?x?3221
2(b?1)x?x?21
2(b?1)?0
x(x?1)?
x(x?1)?221?1?2(b?1)x?x?(b?1)?0 ?2?2??1?(b?1)x?2x?(b?1)??0?2?
b(???1)x??1 ?02 十字相乘法分解:x2(x?1)?1
2?(b?1x)?
1?21?(x?1)x?(b?1)x?(b?1)?0 ??22???x?31
2(b?1)x?x?
22121
2(b?1)?0恒有含x??1的三个不等实根 (b?1)?0有两个不等于-1的不等实根。 等价于x?1
2(b?1)x?
11?2??(b?1)?4?(b?1)?0??42?b?(??,?1)?(?1,3)?(3,??) ??11?(?1)2?(b?1)?(b?1)?0??22
题型二:切线的条数问题====以切点x为未知数的方程的根的个数 0
例7、已知函数f(x)?ax?bx?cx在点x0处取得极小值-4,使其导数f'(x)?0的x的取值范围为(1,3),求:(1)
f(x)的解析式;(2)若过点P(?1,m)可作曲线y?f(x)的三条切线,求实数m的取值范围. 32
(1)由题意得:f'(x)?3ax?2bx?c?3a(x?1)(x?3),(a?0)
∴在(??,1)上f'(x)?0;在(1,3)上f'(x)?0;在(3,??)上f'(x)?0 因此f(x)在x0?1处取得极小值?4
∴a?b?c??4①,f'(1)?3a?2b?c?0②,f'(3)?27a?6b?c?0③
?a??1
?32由①②③联立得:?b?6,∴f(x)??x?6x?9x
?c??9?
,2
22222 32(2)设切点Q(t,f(t)),y?f(t)?f(t)(x?t)y?(?3t?12t?9)(x?t)?(?t?6t?9t) ?(?3t?12t?9)x?t(3t?12t?9)?t(t?6t?9)?(?3t?12t?9)x?t(2t?6t)过(?1,m) m?(?3t?12t?9)(?1)?2t?6t
g(t)?2t?2t?12t?9?m?0令g'(t)?6t?6t?12?6(t?t?2)?0, 32222322
求得:t??1,t?2,方程g(t)?0有三个根。
??2?3?12?9?m?0?m?16???? g(2)?016?12?24?9?m?0m??11???
故:?11?m?16;因此所求实数m的范围为:(?11,16) 需:??g(?1)?0
题型三:已知f(x)在给定区间上的极值点个数则有导函数=0的根的个数 解法:根分布或判别式法
例8、
9
17
解:函数的定义域为R(Ⅰ)当m=4时,f (x)= x3-2+10x,
32
2
f?(x)=x-7x+10,令f?(x)?0 , 解得x?5,或x?2. 令f?(x)?0 , 解得2?x?5
可知函数f(x)的单调递增区间为(??,2)和(5,+∞),单调递减区间为?2,5?. (Ⅱ)f?(x)=x2-(m+3)x+m+6,
要使函数y=f (x)在(1,+∞)有两个极值点,?f?(x)=x2-(m+3)x+m+6=0的根在(1,+∞)
根分布问题:
?
???(m?3)2?4(m?6)?0;?
则?f?(1)?1?(m?3)?m?6?0;, 解得m>3 ?m?3??1.?2
例9、已知函数
(2)令g(x)=
'
f(x)?
a3
x?
3
12
x,(a?R,a?0)(1)求f(x)的单调区间;
2
14
x4+f(x)(x∈R)有且仅有3个极值点,求a的取值范围.
2
解:(1)f(x)?ax?x?x(ax?1)
'
当a?0时,令f(x)?0解得x??
1a
1a
或x?0,令f(x)?0解得?
1a
'
1a
?x?0,
所以f(x)的递增区间为(??,?)?(0,??),递减区间为(?
1a
,0).
1a
?当a?0时,同理可得f(x)的递增区间为(0,),递减区间为(??,0)?(?,??).
(2)g(x)?
3
14
x?
2
4
a3
x?
3
12
x有且仅有3个极值点
2
2
2
?g?(x)?x?ax?x?x(x?ax?1)=0有3个根,则x?0或x?ax?1?0,a??2
方程x?ax?1?0有两个非零实根,所以??a?4?0,
?a??2或a?2
而当a??2或a?2时可证函数y?g(x)有且仅有3个极值点
22
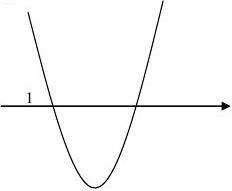

10
其它例题:
(一)最值问题与主元变更法的例子.
已知定义在R上的函数f(x)?ax?2ax?b(a?0)在区间??2,1?上的最大值是5,最小值是-11.
3
2
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若t?[?1,1]时,f?(x)?tx?0恒成立,求实数x的取值范围. 解:(Ⅰ)?f(x)?ax?2ax?b,?f(x)?3ax?4ax?ax(3x?4)
'
令f(x)=0,得x1?0,x2?
3
2
'
2
43
???2,1?
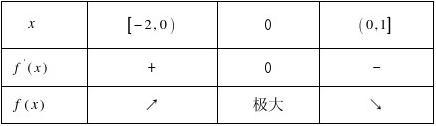
因此f(0)必为最大值,∴f(0)?5因此b?5, ?f(?2)??16a?5,f(1)??a?5,?f(1)?f(?2),
即f(?2)??16a?5??11,∴a?1,∴ f(x)?x?2x?5.
22
(Ⅱ)∵f?(x)?3x?4x,∴f?(x)?tx?0等价于3x?4x?tx?0,
3
2
令g(t)?xt?3x?4x,则问题就是g(t)?0在t?[?1,1]上恒成立时,求实数x的取值范围,
?3x2?5x?0?g(?1)?0
为此只需?,即?2,
g(1)?0x?x?0??
2
解得0?x?1,所以所求实数x的取值范围是[0,1]. (二)根分布与线性规划例子
例:已知函数f(x)?
23
x?ax?bx?c
32
(Ⅰ) 若函数f(x)在x?1时有极值且在函数图象上的点(0,1)处的切线与直线3x?y?0平行, 求f(x)的解析式;
11
(Ⅱ) 当f(x)在x?(0,1)取得极大值且在x?(1,2)取得极小值时, 设点M(b?2,a?1)所在平面区域为S,
经过原点的直线L将S分为面积比为1:3的两部分, 求直线L的方程.
2
解: (Ⅰ). 由f?(x)?2x?2ax?b, 函数f(x)在x?1时有极值 ,
∴ 2a?b?2?0 ∵ f(0)?1 ∴ c?1 又∵ f(x)在(0,1)处的切线与直线3x?y?0平行, ∴ f?(0)?b??3 故 a?
23
3
12
∴ f(x)?x?
12
x?3x?1 ……………………. 7分
1)取得极大值且在x?(1,
2)取得极小值,
2
2
(Ⅱ) 解法一: 由f?(x)?2x?2ax?b 及f(x)在x?(0,
?f?(0)?0?
∴ ?f?(1)?0 即
?f?(2)?0??b?0?
?2a?b?2?0 令M(x,?4a?b?8?0?
?x?b?2
y), 则 ?
y?a?1?
?x?2?0
?a?y?1?∴ ? ∴ ?2y?x?2?0 故点M所在平面区域S为如图△ABC,
?b?x?2?4y?x?6?0
?
易得A(?2,0), B(?2,?1), C(2,?2), D(0,?1), E(0,?
32
), S?ABC?2
同时DE为△ABC的中位线, S?DEC?∴ 所求一条直线L的方程为:
x?0
13
S四边形ABED
另一种情况设不垂直于x轴的直线L也将S分为面积比为1:3的两部分, 设直线L方程为y?kx,它与AC,BC分别交于F、G, 则 k?0, S四边形DEGF?1
由 ?
?y?kx?2y?x?2?0?y?kx?4y?x?6?0
得点F的横坐标为: xF??
22k?1
由 ? 得点G的横坐标为: xG??
12
32
6
64k?1
22k?1
12
∴S四边形DEGF?S?OGE?S?OFD ?解得: k?
12
??
4k?1
?
12
?1?
?1即 16k?2k?5?0
2
或 k??
58
(舍去) 故这时直线方程为: y?
12
x
综上,所求直线方程为: x?0或y?x .…………….………….12分
1)取得极大值且在x?(1,
2)取得极小值,
2
(Ⅱ) 解法二: 由f?(x)?2x?2ax?b 及f(x)在x?(0,
12
?f?(0)?0?
∴ ?f?(1)?0 即
?f?(2)?0??b?0?
?2a?b?2?0 令M(x,?4a?b?8?0?
?x?b?2
y), 则 ?
y?a?1?
?x?2?0
?a?y?1?∴ ? ∴ ?2y?x?2?0 故点M所在平面区域S为如图△ABC,
?b?x?2?4y?x?6?0
?
易得A(?2,0), B(?2,?1), C(2,?2), D(0,?1), E(0,?
32
), S?ABC?2
同时DE为△ABC的中位线, S?DEC?
13
S四边形ABED ∴所求一条直线L的方程为: x?0 12
x, 设直线BO与AC交于H ,
另一种情况由于直线BO方程为: y?
1?
?y?x由 ? 得直线L与AC交点为: H(?1,2
?2y?x?2?0?
?
12
)
∵ S?ABC?2, S?DEC?
12
?
12
?2?
12
12
, S?ABH?S?ABO?S?AOH?
12
?2?1?
12
?2?
12
?
12
∴ 所求直线方程为: x?0 或y?(三)根的个数问题
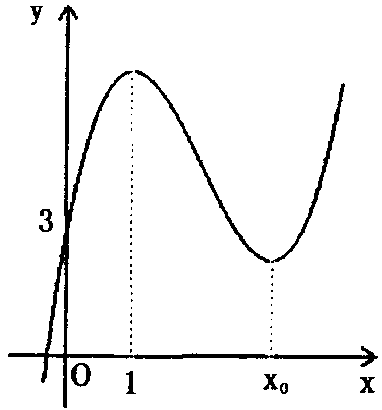
x
例 已知函数f(x)?ax?bx?(c?3a?2b)x?d (a?0)的图象如图所示。
(Ⅰ)求c、d的值;
(Ⅱ)若函数f(x)的图象在点(2,f(2))处的切线方程为3x?y?11?0,求函数f ( x )的解析式;
(Ⅲ)若x0?5,方程f(x)?8a有三个不同的根,求实数a的取值范围。 解:由题知:f?(x)?3ax?2bx+c-3a-2b
(Ⅰ)由图可知 函数f ( x )的图像过点( 0 , 3 ),且f??1?= 0
得?
?d?3??
?3a?2b?c?3a?2b?0?c?0?d?3
2
32
(Ⅱ)依题意
f??2?= – 3 且f ( 2 ) = 5
?12a?4b?3a?2b??3
解得a = 1 , b = – 6 ?
?8a?4b?6a?4b?3?5
所以f ( x ) = x3 – 6x2 + 9x + 3
32
(Ⅲ)依题意 f ( x ) = ax + bx – ( 3a + 2b )x + 3 ( a>0 )
2
f??x?= 3ax + 2bx – 3a – 2b 由f??5?= 0?b = – 9a ①
若方程f ( x ) = 8a有三个不同的根,当且仅当 满足f ( 5 )<8a<f ( 1 ) ②
由① ② 得 – 25a + 3<8a<7a + 3?所以 当
111
111
<a<3
<a<3时,方程f ( x ) = 8a有三个不同的根。???? 12分
(四)根的个数问题
13
例:已知函数f(x)?132
3x?ax?x?1(a?R)
(1)若函数f(x)在x?x1,x?x2处取得极值,且x1?x2?2,求a的值及f(x)的单调区间;
(2)若a?125
2,讨论曲线f(x)与g(x)?1
2x?(2a?1)x?6(?2?x?1)的交点个数.
解:(1)f'(x)?x2?2ax?1
?x1?x2?2a,x1?x2??
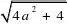
1
?x1?x2???2
?a?0???????????????????????????2分 f?(x)?x2?2ax?1?x2?1
令f?(x)?0得x??1,或x?1
令f?(x)?0得?1?x?1
∴f(x)的单调递增区间为(??,?1),(1,??),单调递减区间为(?1,1)????5分
(2)由题f(x)?g(x)得132125
3x?ax?x?1?2x?(2a?1)x?6 即112x?1
3x3?(a?2)x?2a6?0 令?(x)?1x3?(a?1)x21
32?2ax?6(?2?x?1)????????6分 ???(x)?x2?(2a?1)x?2a?(x?2a)(x?1)
令??(x)?0得x?2a或x?1?????????????????7分 ?a?1
2

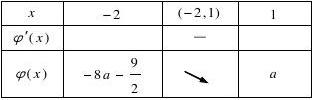
此时,?8a?9
2?0,a?0,有一个交点;??????????9分
当2a??2即?1?a?1
时,
?2a21
3(3?2a)?6?0,
∴当?8a?9
2?0即?1?a??9
16时,有一个交点;
当?8a?9?0,且a?0即?9
216?a?0时,有两个交点;
14
当0?a?综上可知,当a?? 当?9
16129时,?8a?或0?a?9212?0,有一个交点.?????????13分 16时,有一个交点; ?a?0时,有两个交点.?????????????14分
(五)简单切线问题 已知函数f(x)?x
a32图象上斜率为3的两条切线间的距离为25,函数g(x)?f(x)?3bx
a2?3.
(Ⅰ) 若函数g(x)在x?1处有极值,求g(x)的解析式; (Ⅱ) 若函数g(x)在区间[?1,1]上为增函数,且b?mb?4?g(x)在区间[?1,1]上都成立,求实数m的取值范围.
2
15
