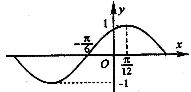
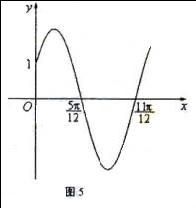
★三角函数图像变换小结★
相位变换:
①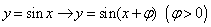 将
将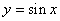 图像沿
图像沿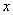 轴向左平移
轴向左平移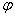 个单位
个单位
②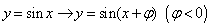 将
将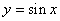 图像沿
图像沿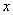 轴向右平移
轴向右平移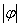 个单位
个单位
周期变换:
①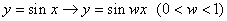 将
将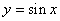 图像上所有点的纵坐标不变,横坐标伸长为原来的
图像上所有点的纵坐标不变,横坐标伸长为原来的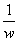 倍
倍
②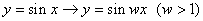 将
将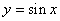 图像上所有点的纵坐标不变,横坐标缩短为原来的
图像上所有点的纵坐标不变,横坐标缩短为原来的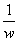 倍
倍
振幅变换:
①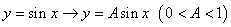 将
将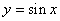 图像上所有点的横坐标不变,纵坐标缩短为原来的
图像上所有点的横坐标不变,纵坐标缩短为原来的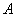 倍
倍
②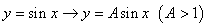 将
将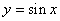 图像上所有点的横坐标不变,纵坐标伸长为原来的
图像上所有点的横坐标不变,纵坐标伸长为原来的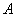 倍
倍
【特别提醒】
由y=sinx的图象变换出y=Asin(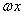 +
+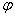 )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现
途径一:先平移变换再周期变换(伸缩变换)
先将y=sinx的图象向左(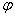 >0)或向右(
>0)或向右(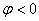 )平移|
)平移|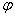 |个单位,再将图象上各点的横坐标变为原来的
|个单位,再将图象上各点的横坐标变为原来的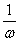 倍(
倍(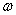 >0),便得y=sin(ωx+
>0),便得y=sin(ωx+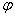 )的图象
)的图象

途径二:先周期变换(伸缩变换)再平移变换
先将y=sinx的图象上各点的横坐标变为原来的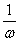 倍(
倍(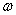 >0),再沿x轴向左(
>0),再沿x轴向左(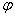 >0)或向
>0)或向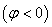 右平移
右平移 个单位,便得y=sin(
个单位,便得y=sin(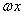 +
+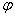 )的图象
)的图象

【特别提醒】若由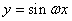 得到
得到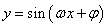 的图象,则向左或向右平移应平移
的图象,则向左或向右平移应平移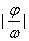 个单位
个单位
为了得到函数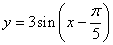 的图像,只要把
的图像,只要把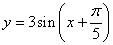 上所有的点( )
上所有的点( )
(A)向右平行移动 个单位长度 (B)向左平行移动
个单位长度 (B)向左平行移动 个单位长度
个单位长度
(C)向右平行移动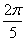 个单位长度 (D)向左平行移动
个单位长度 (D)向左平行移动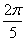 个单位长度
个单位长度
(2011·朝阳期末)要得到函数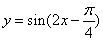 的图象,只要将函数
的图象,只要将函数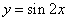 的图象 ( )
的图象 ( )
…… …… 余下全文

 ; (2)
; (2) (2)y=
(2)y=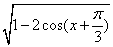 (4)y=
(4)y=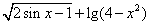
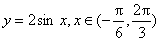 (2)y=2sin(2x-
(2)y=2sin(2x- ),x
),x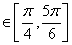 (3)
(3) 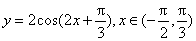
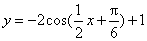 的最大值以及此时x的取值集合
的最大值以及此时x的取值集合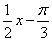 ) (3)y=tan(2x
) (3)y=tan(2x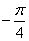 ) (4)y=
) (4)y=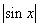
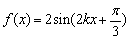 的最小正周期
的最小正周期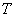 满足
满足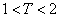 ,则自然数
,则自然数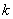 的值为______.
的值为______.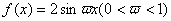 在区间
在区间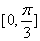 上的最大值是
上的最大值是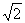 ,则
,则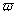 =________.
=________. 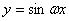 (ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为【 】
(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为【 】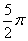 B.
B.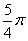 C.π D.
C.π D.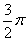
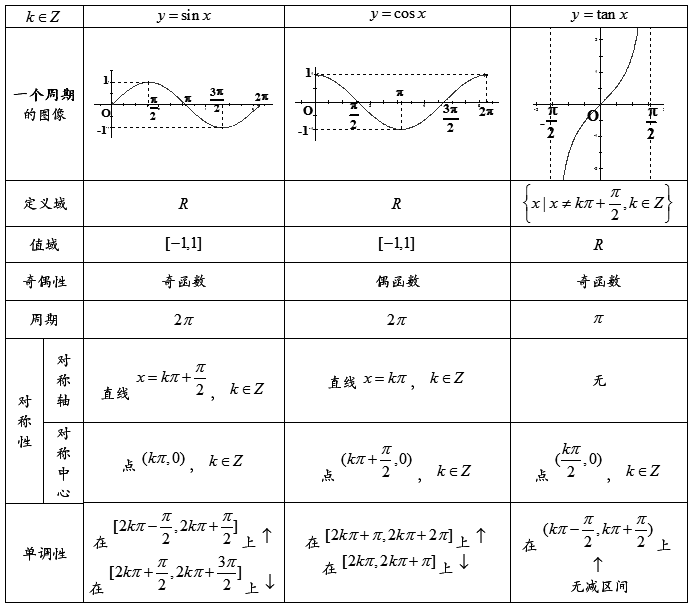
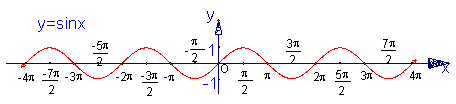
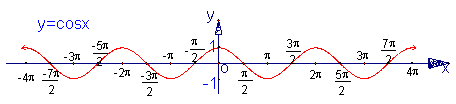
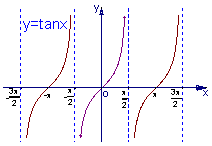
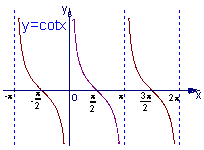
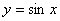 的递增区间是
的递增区间是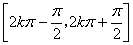
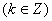 ,
,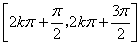
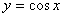 的递增区间是
的递增区间是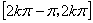
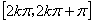
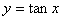 的递增区间是
的递增区间是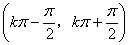
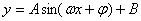
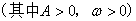
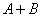 ,最小值是
,最小值是 ,周期是
,周期是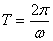 ,频率是
,频率是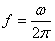 ,相位是
,相位是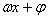 ,初相是
,初相是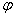 ;其图象的对称轴是直线
;其图象的对称轴是直线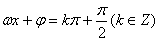 ,凡是该图象与直线
,凡是该图象与直线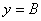 的交点都是该图象的对称中心。
的交点都是该图象的对称中心。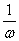 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+ 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+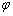 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(-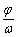 ,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
,0)作为突破口,要从图象的升降情况找准第一个零点的位置。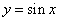 的对称轴为
的对称轴为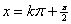 ,对称中心为
,对称中心为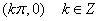 ;
;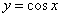 的对称轴为
的对称轴为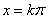 ,对称中心为
,对称中心为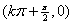 ;
;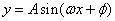 和
和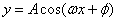 来说,对称中心与零点相联系,对称轴与最值点联系。
来说,对称中心与零点相联系,对称轴与最值点联系。 的正负利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间;
的正负利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间;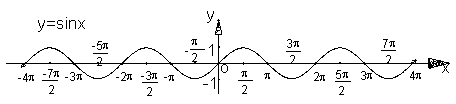
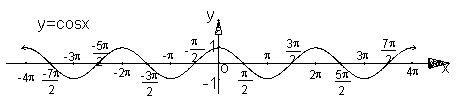
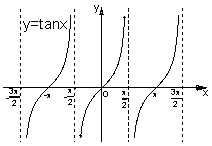
 的递增区间是
的递增区间是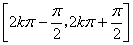
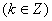 ,递减区间是
,递减区间是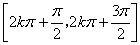
 的递增区间是
的递增区间是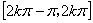
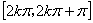
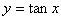 的递增区间是
的递增区间是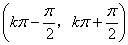
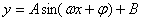
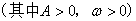
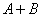 ,最小值是
,最小值是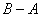 ,周期是
,周期是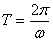 ,频率是
,频率是 ,相位是
,相位是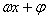 ,初相是
,初相是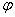 ;其图象的对称轴是直线
;其图象的对称轴是直线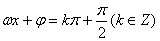 ,凡是该图象与直线
,凡是该图象与直线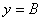 的交点都是该图象的对称中心。
的交点都是该图象的对称中心。 无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。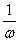 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+ 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+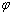 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(- ,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
,0)作为突破口,要从图象的升降情况找准第一个零点的位置。 的对称轴为
的对称轴为 ,对称中心为
,对称中心为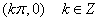 ;
;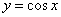 的对称轴为
的对称轴为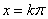 ,对称中心为
,对称中心为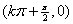 ;
;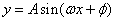 和
和 来说,对称中心与零点相联系,对称轴与最值点联系。
来说,对称中心与零点相联系,对称轴与最值点联系。 的正负
的正负
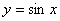 的递增区间是
的递增区间是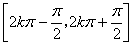
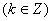 ,递减区间是
,递减区间是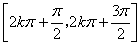
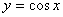 的递增区间是
的递增区间是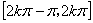
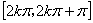
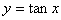 的递增区间是
的递增区间是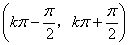
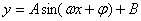
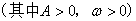
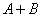 ,最小值是
,最小值是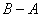 ,周期是
,周期是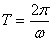 ,频率是
,频率是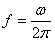 ,相位是
,相位是 ,初相是
,初相是 ;其图象的对称轴是直线
;其图象的对称轴是直线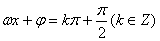 ,凡是该图象与直线
,凡是该图象与直线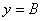 的交点都是该图象的对称中心。
的交点都是该图象的对称中心。 无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。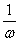 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+ 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+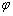 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(-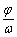 ,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
,0)作为突破口,要从图象的升降情况找准第一个零点的位置。 的对称轴为
的对称轴为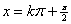 ,对称中心为
,对称中心为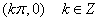 ;
;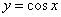 的对称轴为
的对称轴为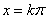 ,对称中心为
,对称中心为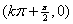 ;
;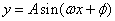 和
和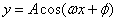 来说,对称中心与零点相联系,对称轴与最值点联系。
来说,对称中心与零点相联系,对称轴与最值点联系。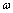 的正负
的正负
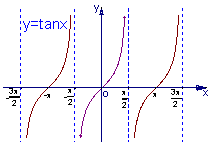
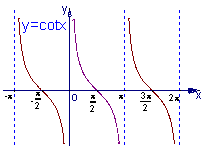
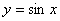 的递增区间是______________________________
的递增区间是______________________________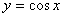 的递增区间是__________________________________
的递增区间是__________________________________ 的递增区间是____________________________________
的递增区间是____________________________________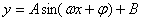
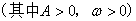
 的交点都是该图象的对称中心
的交点都是该图象的对称中心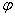 )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换